Куцый Н.Н. Теория оптимального управления
Подождите немного. Документ загружается.

В качестве примера применения необходимых условий исследуем функционал
( )
∫
′
+
′
=
2
1
22
172 dxyxyI).(
при граничных условиях
11
=
)(y
,
22
=
)(y
.
Для функционала (2.17) определяем производные
yxF
y
′
+=
′
2
21
,
2
2xF
yy
=
′′
. В
заданном интервале
021
>≤≤
′′
yy
Fx
, следовательно, на экстремалях может дости-
гаться минимум функционала.
Уравнение Эйлера в данном примере имеет вид
02 182
2
=
′
+
′′
yxyx).(
.
Общее решение уравнения (2.18) можно записать в форме
2
1
C
x
C
y
+=
.
Из граничных условий получим два уравнения для определения
1
C
и
2
C
:
=+
=+
.
,
).(
2
2
1
192
2
1
21
С
С
CC
Решение системы (2.19) даёт
2
1
−=
C
,
3
2
=
C
. Тогда уравнение экстремали име-
ет вид
x
y
2
3
−=
.
Рассмотрим третье необходимое условие экстремума функционала – условие
Вейерштрасса. Если линия
)(xyy
=
доставляет сильный минимум (максимум) функ-
ционалу (2.1), т.е.
∫
′
=
2
1
x
x
dxyyxFyI ),,()(
,
то функция Вейерштрасса
),,()(),,(),,(),,,( yyxFykyyxFkyxFkyyxE
y
′′
−−
′
−=
′
′
при произвольных конечных значениях
k
во всех точках
),( yx
экстремали неотри-
цательна (неположительна).
Отметим, что необходимое условие слабого минимума является в то же время
необходимым условием сильного минимума, но не обратно.
11

В качестве четвертого необходимого условия экстремума функционала рассмот-
рим условие Якоби. Если линия
)(xyy
=
доставляет сильный минимум (максимум)
функционалу (2.1), т.е.
∫
′
=
2
1
x
x
dxyyxFyI ),,()(
,
вторая вариация (2.5), т.е.
( )
∫
′
+
′′
+
′′
=
′′′
2
1
22
2
2
2
x
x
yyyyyy
dxyyxFyyxFyyxF
d
Фd
ηηηη
α
)
~
,
~
,()
~
,
~
,()
~
,
~
,(
,
в точке
0
=
α
должна быть неотрицательной:
( )
02 202
2
1
222
≥+
′
+=
∫
′′′
x
x
yyyyyy
dxFFFI
ηηηηδ
).(
,
0( 212
21
==
)()).( xx
ηη
.
Функции
)(x
η
, для которых
0
2
=
I
δ
и выполняются условия (2.21), доставляют
минимум функционалу (2.20). Уравнение Эйлера для функционала
I
2
δ
( )
0
=
′
+−
′
+
′′′′
ηηηη
yyyyyyyy
FF
dx
d
FF
называется уравнением Якоби.
При выполнении условия Лежандра
0
≠
′′
yy
F
,
21
xxx
≤≤
из условий
0(
11
=
′
=
)() xx
ηη
следует, что
0(
=
)x
η
. Точки
))(,(
111
xyxM
и
))(,(
11
xyxM
′′′
на экстремали
)(xyy
=
называются сопряженными, если
0(
11
=
′
=
)() xx
ηη
,
причём
0(
≠
)x
η
,
11
xxx
′
<<
.
Условие Якоби заключается в следующем. Если экстремаль
)(xyy
=
,
21
xxx
≤≤
доставляет минимум функционалу (2.1), т.е.
∫
′
=
2
1
x
x
dxyyxFyI ),,()(
,
12
то она не содержит точек, сопряженных точке
))(,(
11
xyx
.
13
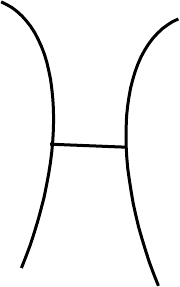
3. ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ КОНЦАМИ
В вариационных задачах с подвижными концами рассматривается функционал,
который зависит от линий
E
:
∫
′
=
E
dxyyxFEI ),,()().( 13
,
где линия
E
перемещается так, что её концы движутся вдоль двух заданных линий
C
и
D
(рис. 3.1). Требуется найти среди линий
E
такую линию, которая доставляет экс-
тремум функционалу (3.1). В отношении подынтегральной функции предполагается
её непрерывность по совокупности аргументов, а также существование и непрерыв-
ность её частных производных до третьего порядка включительно.
В такой постановке задачи общее уравнение Эйлера, которое является нелиней-
ным дифференциальным уравнением второго порядка, зависит от двух произвольных
постоянных, определяемых из условий трансверсальности.
Определим условия трансверсальности. С этой целью зададим перемещение ли-
нии
E
с помощью параметра
a
так, что однопараметрическое семейство линий
),( axyy
=
относит каждому значению параметра одно из возможных положений ли-
нии
E
. Если параметр
t
будет определять положение точки на линии
C
, то абсцисса
этой точки и параметр
a
являются функциями
t
. В этом случае линии
C
и
D
заданы
соответственно параметрическими уравнениями
)(txx
1
=
,
)())(),(( tytatxyy
11
==
,
)(txx
2
=
,
)())(),(( tytatxyy
22
==
,
21
ttt
≤≤
.
На семействе линий
),( axyy
=
функционал превращается в функцию
t
E
C
D
Рис. 3.1.

∫
′
==
)(
)(
)),(),(,()().(
tx
tx
dxaxyaxyxFtEI
2
1
)Ф( 23
.
Дифференцируя по
t
соотношение (3.2), имеем
( )
∫
′
++
′
=
′
′
2
1
2
1
)(Ф 33
x
x
ayay
x
x
dxyFyF
dt
da
dt
dx
axyaxyxFt )),(),(,().(
.
Подынтегральное выражение в соотношении (3.3) с учётом уравнения Эйлера
(2.12), т.е.
0
=−
′
yy
F
dx
d
F
можно представить в виде
( ) ( )
ayayayayay
yF
dx
d
yFyF
dx
d
yFyF
′′′′
=
′
+=
′
+
43 ).(
.
Подстановка (3.4) в выражение (3.3) даёт соотношение
dt
da
a
y
F
dt
dx
axyaxyxFt
x
x
y
x
x
2
1
2
1
)(Ф 53
∂
∂
+
′
=
′
′
)),(),,(,().(
.
Выражение (3.5) преобразуем с учётом соотношения
dt
da
y
dt
dx
y
dt
dy
ax
+=
или
dt
dx
y
dt
dy
dt
da
y
a
′
−=
63 ).(
.
Тогда подстановка (3.6) в выражение (3.5) даёт
2
1
)(Ф 73
x
x
y
dt
dx
y
dt
dy
F
dt
dx
yyxFt
′
−+
′
=
′
′
),,().(
Если линия
E
доставляет экстремум функционалу (3.1), т.е.
∫
′
=
E
dxyyxFEI ),,()(
,
то
0)Ф( 83
0
==
=
tt
tdEdI )().(
15

при любых
1
dx
и
2
dx
.
Выбрав
0
1
=
dx
при
0
2
≠
dx
или
0
1
≠
dx
при
0
2
=
dx
и учтя соотношение (3.7),
т.е.
2
1
)(Ф
x
x
y
dt
dx
y
dt
dy
F
dt
dx
yyxFt
′
−+
′
=
′
′
),,(
,
из условия экстремума функционала (3.8) , т.е.
0)Ф( 83
0
==
=
tt
tdEdI )().(
,
получим следующие условия трансверсальности:
=
′
−
′
+
′
=
′
−
′
+
′
′
′
.))(,,(),,(
,))(,,(),,(
).(
0
0
93
2222222222
1111111111
dxydyyyxFdxyyxF
dxydyyyxFdxyyxF
y
y
Эти условия позволяют определить положение концов экстремали путём вычис-
ления двух произвольных постоянных, от которых зависит общее решение уравнения
Эйлера, так как оно является дифференциальным уравнением второго порядка.
Если заданы уравнения
)(xy
ϕ
=
линии
C
и
)(xy
ψ
=
линии
D
, то с учётом со-
отношений
11
dxxdy )(
ϕ
′
=
и
22
dxxdy )(
ψ
=
условия трансверсальности (3.9) примут
вид
=
′′
−
′
+
′
=
′′
−
′
+
′
=
′
=
′
.),,()(),,(
,),,()(),,(
0
0
2
1
111111
111111
xx
y
xx
y
yyxFyyyxF
yyxFyyyxF
ψ
ϕ
Если линия
C
задана уравнением
0
1
=
),( yxw
, а линия
D
- уравнением
0
2
=
),( yxw
, то (3.9) получим в форме
y
y
x
y
w
F
w
FyF
11
′′
=
′
−
,
y
y
x
y
w
F
w
FyF
22
′′
=
′
−
.
В случае, когда на перемещение концов экстремали не наложены ограничения,
на обоих концах экстремали выполняются условия
0
=
F
,
0
=
′
y
F
.
Рассмотрим теперь в задаче с подвижными концами вариации функционала,
происходящие как от вариации искомой функции, так и от вариации концов.
На рис. 3.2 изображены исходная функция
)(xy
и функция
)()( xhxy
+
, к кото-
рой добавлена вариация
)(xh
. Приращение функционала при переходе от
y
к
hy
+
имеет вид
16
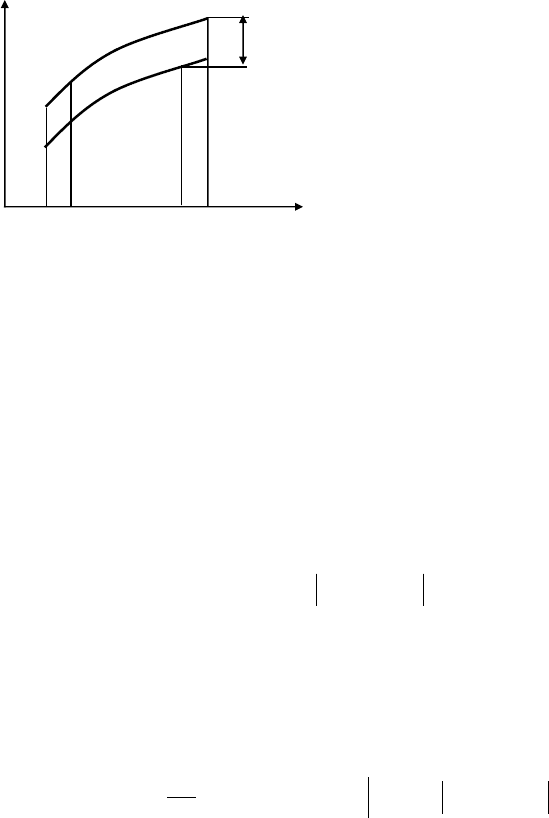
−
′
+
′
+=−+=∆
∫
+
+
11
00
xx
xx
dxhyhyxFyIhyII
δ
δ
),,()()(
+
′
−
′
+
′
+=
′
−
∫∫∫
1
0
1
0
1
0
x
x
x
x
x
x
dxyyxFdxhyhyxFdxyyxF ),,(),,(),,(
∫∫
+
+
′
+
′
+−
′
+
′
++
00
0
11
1
xx
x
xx
x
dxhyhyxFdxhyhyxF
δ
δ
),,(),,(
.
Выделим главную,
линейную, часть прираще-
ния функционала, его пер-
вую вариацию
01
01
1
0
xFxFdxhFhFI
xx
x
x
yy
δδδ
−+
′
+=
∫
′
)(
.
После того как второй член подынтегрального выражения проинтегрируем по
частям, первая вариация функционала примет вид
01
01
1
0
1
0
xFxFhFhdxF
dx
d
FI
xx
x
x
y
x
x
yy
δδδ
−++
−=
′′
∫
.
Так как с точностью до бесконечно малых высшего порядка
000
xyyxh
δδ
′
−=
)(
и
111
xyyxh
δδ
′
−=
)(
, то вариацию функционала можно записать в виде
17
0
x
0
x
0
+
δ
x
0
x
1
x
1
+
δ
x
1
x
)(xy
y(x)+h(x)
δ
y
1
Рис.
3.2
( )
−−
′
−++
−=
′′′′
∫
011
011
1
0
103 yFxFyFyFhdxF
dx
d
FI
x
y
x
y
x
y
x
x
yy
δδδδ
).(
( )
0
0
xFyF
x
y
δ
′
′
−−
.
Выражение (3.10) для вариации функционала состоит из интегрального члена,
происходящего от вариации
)(xy
внутри исходного промежутка интегрирования, и
членов от вариации его концов.
Из рассмотрения (3.10) также могут быть получены условия трансверсальности в
задаче с подвижными концами. Пусть необходимо найти экстремум функционала
среди кривых
)(xy
концы которых перемещаются по линиям
)(xy
ϕ
=
и
)(xy
ψ
=
.
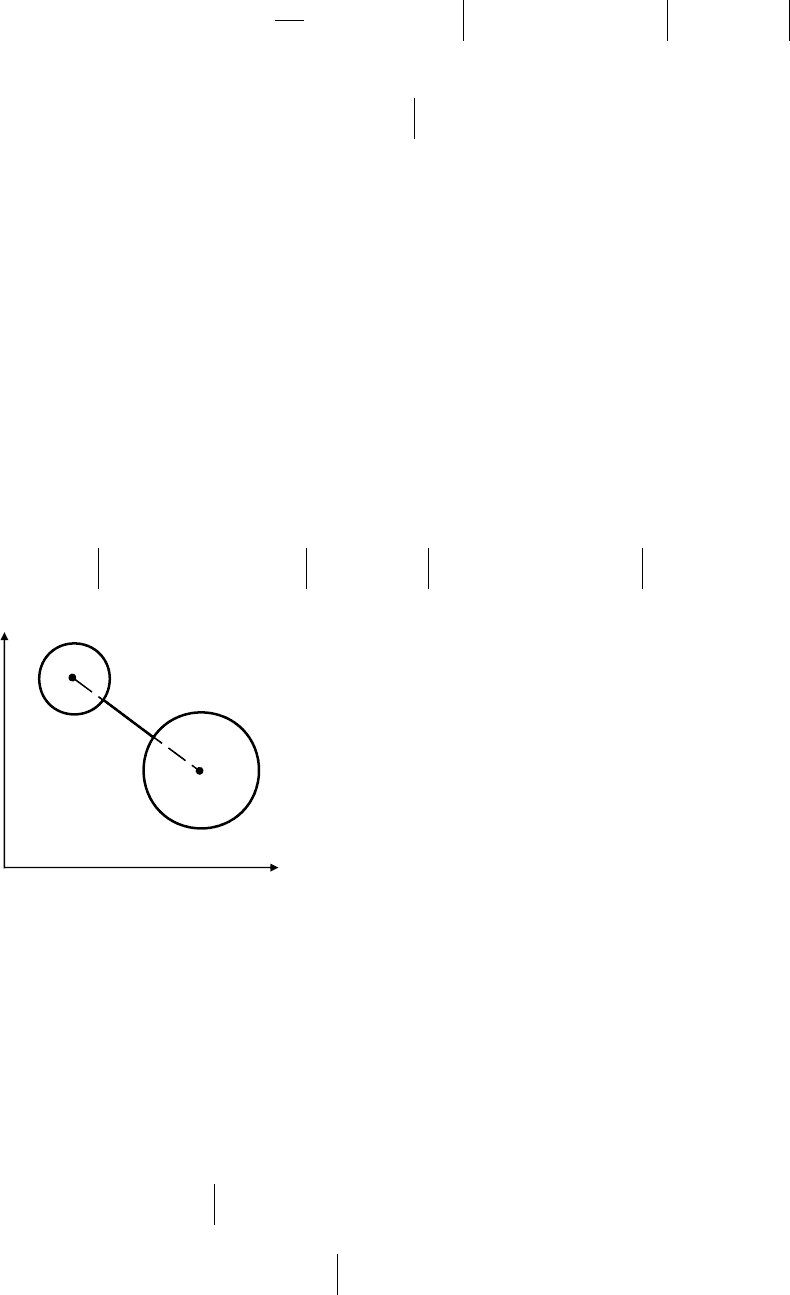
Примером такой задачи может служить задача о нахождении кратчайшего расстоя-
ния, например, между двумя окружностями (рис. 3.3).
Решением задачи является экстремаль, которая проходит через точки
A
и
B
.
Согласно уравнению Эйлера, на экстремали интегральной член выражения (3.10) об-
ращается в нуль, и вариация функционала примет вид
0011
0011
xFyFyFxFyFyFI
x
y
x
y
x
y
x
y
δδδδδ
)()(
′′′′
′
−−−
′
−+=
.
Учитывая, что с точно-
стью до бесконечно малых
высшего порядка
00
xxy
δϕδ
)(
′
=
,
11
xxy
δψδ
)(
′
=
,
вариацию функционала
можно записать в виде
−
′
−+
′
=
′′
1
1
xFyFFI
x
yy
δψδ
)(
0
0
xFyFF
x
yy
δϕ
)(
′′
′
−+
′
−
.
18
y
x
0
O
1
O
2
A
B
Рис. 3.3
Так как
0
x
δ
и
−
1
x
δ
независимые друг от друга вариации, то из условия экстре-
мума
0
=
I
δ
получим условие трансверсальности
0
0
=
′
−
′
+
′
x
y
FyF )(
ϕ
,
0
1
=
′
−
′
+
′
x
y
FyF )(
ψ
.
В качестве примера запишем условия трансверсальности для функционалов вида
∫
′
+=
1
0
2
1
x
x
dxyyxfI ),(
.
В этом случае
2
2
1
1
y
yF
y
y
yxfF
y
′
+
′
=
′
+
′
=
′
),(
,
и условия трансверсальности имеют вид
0
1
1
2
=
′
+
′′
+
y
yF )(
ϕ
,
0
1
1
2
=
′
+
′′
+
y
yF )(
ψ
.
Отсюда следует, что на левом конце
ϕ
′
−=
′
1
y
, на правом -
ψ
′
−=
′
1
y
. Это озна-
чает, что экстремаль ортогональна к кривым
)(x
ϕ
и
)(x
ψ
, т.е. пересекает их под пря-
мым углом.
19
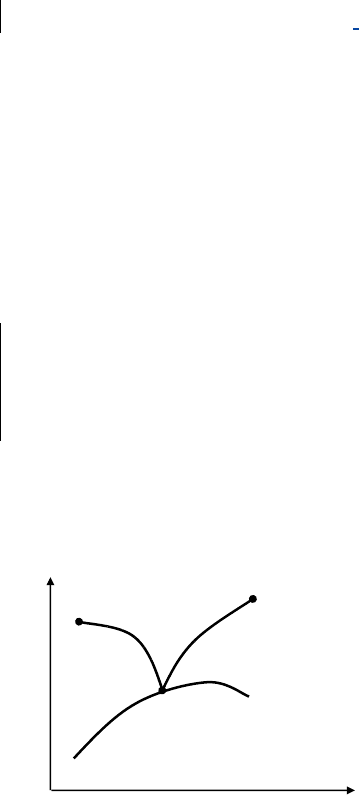
4.ЛОМАНЫЕ ЭКСТРЕМАЛИ
До сих пор рассматривались вариационные задачи, в которых искомая функция
)(xy
предполагалась непрерывной и имеющей непрерывную производную.
В некоторых классах последнее требование может не выполняться и решение
достигается на экстремалях, имеющих угловые точки. К числу таких задач принадле-
жат, например, задачи на отражение и преломление экстремалей, и эти задачи являют-
ся обобщением задач на отражение и преломление света.
В задаче об отражении экстремалей требуется найти кривую, реализующую экс-
тремум функционала
∫
′
=
2
0
x
x
dxyyxFyI ),,()(
и проходящую через заданные точки
),(
00
yxA
и
),(
22
yxB
таким образом, что
кривая должна попасть в точку
B
лишь после отражения от заданной линии
)(xy
ϕ
=
(рис. 4.1).
В точке отражения
),(
11
yxC
левая производная
)( 0
1
−
′
xy
и правая произ-
водная
)( 0
1
+
′
xy
различны.
Поэтому представим функ-
ционал в виде суммы двух
интегралов
∫∫
′
+
′
=
2
1
1
0
x
x
x
x
dxyyxFdxyyxFI ),,(),,(
B(x
2
,y
2
)
A(x
0
,y
0
)
C(x
1
,y
1
)
y=φ(x)
x
y
0
Рис. 4.1
