Куцый Н.Н. Теория оптимального управления
Подождите немного. Документ загружается.


МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИРКУТСКИЙ ГОСУДАPСТВЕHHЫЙ
ТЕХНИЧЕСКИЙ УHИВЕPСИТЕТ
ТЕОРИЯ
ТЕОРИЯ
ОПТИМАЛЬНОГО
ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
УПРАВЛЕНИЯ
Иркутск – 2006 г.
Куцый Н.Н. Теория оптимального управления. - Иркутск, изд-во Иркутск. гос.
технич. ун-та, 2006. – 166 с.
Библиогр. 9 назв.
ЛР № 020263 от 30.12.96
Иркутский государственный технический университет
664074, Иркутск, ул. Лермонтова, 83

1.ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Вариационное исчисление определяет условия, при которых функционалы до-
стигают своего экстремума. Функционал определяется следующим образом. На мно-
жестве
M
функций задан функционал, если каждой функции
)(x
ϕ
, принадлежащей
M
,
Mx
∈
)(
ϕ
, соответствует определенное число. Функционал можно рассматривать
как функцию, в которой роль независимых переменных играют другие функции )одна
или несколько). Приведём несколько примеров функционала.
Длина линии
)(xyy
=
,
bxa
≤≤
,
Mxy
∈
)(
, где
−
M
множество функций
)(xy
, определенных на отрезке
],[ ba
и обладающих на нём непрерывной производной
есть функционал
dx
dx
dy
yL
b
a
∫
+=
2
1)(
.
Пусть
S
, пройденный транспортным средством за время
T
, является функцио-
налом скорости
V
транспортного средства
∫
=
T
VdtS
0
.
Время перемещения из одного положения
),(
11
yx
в другое
),(
22
yx
точки в
плоскости
),( yx
, где для каждой пары значений координат
),( yx
скорость точки
),( yxVV
=
задана и не зависит от направления движения, определяется функциона-
лом вида
∫
+
==
∫
2
1
2
1
x
x
L
dx
yxV
dx
dy
yxV
ds
T
),(),(
,
где
22
dydxds
+=
.
Примером функционала более общего вида может служить выражение
∫
′
=
b
a
dxyyxFI ),,(
.
Здесь
−
x
независимая переменная;
−
y
искомая функция
)(xy
;
−
′
y
производная
dx
dy
.
3
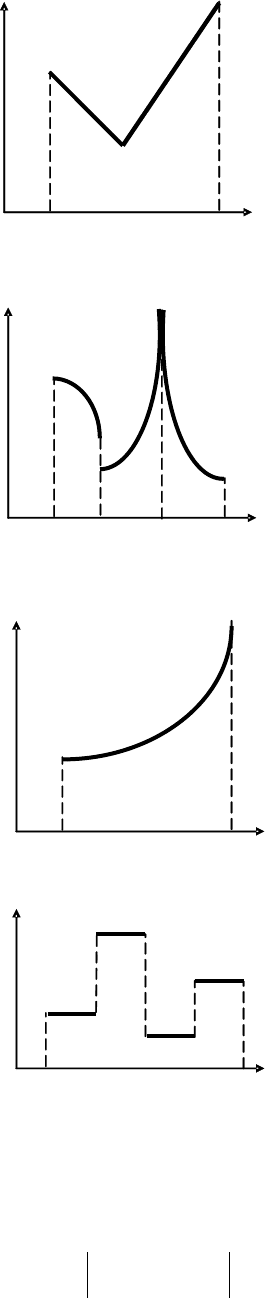
В задачах вариационного исчисления необходимо
указывать, в каком классе функций ищется экстремум
функционала. Рассмотрим следующие классы функций.
Непрерывные функции не имеют разрывов.
Например, функция, изображенная на рис. 1.1, непре-
рывна на отрезке
],[ ba
, а функция на рис. 1.2 имеет
разрывы. Гладкие функции являются не только непре-
рывными, но имеют и непрерывную первую производ-
ную. Гладкая функция приведена на рис. 1.3. Решение
технических задач методами вариационного исчисле-
ния часто приводит к необходимости поиска экстрему-
ма функционала в классах кусочно-непрерывных или
кусочно-гладких функций. Кусочно-непрерывная
функция, которая имеет разрывы в виде скачков пред-
ставлена на рис. 1.4. Кусочно-гладкая функция (рис.
1.1) имеет изломы в отдельных точках.
Рассмотрим классификацию экстремумов функ-
ционала. С этой целью введём понятие функций срав-
нений. если функционал
)(yI
исследуется на экстре-
мум и имеется некоторая функция
)(
*
xy
, которая
подозревается в качестве функции, доставляющей экс-
тремум функционалу, то значение функционала
)(
*
yI
сопоставляется с его значениями на некотором множе-
стве функций
)(xy
, которые называются функциями
сравнения. Множеству функций сравнения принадле-
жит также и исследуемая функция
)(
*
xy
. На множе-
стве функций сравнения существует положительная
(отрицательная) разность
)()(
*
yIyII
−=∆
,
если имеет место минимум (максимум_ функционала
)(yI
при
)(
*
xy
.
Окрестностью нулевого порядка или сильной
окрестностью
)(
*
xy
называется множество непрерыв-
ных функций сравнения
)(xy
таких, что при некотором положительном числе
ε
имеет место неравенство
ε
<−
)()(
*
xyxy
,
21
xxx
≤≤
.
4
y
0
x
a
b
Рис. 1.1
y
0
x
a
b
Рис. 1.2
x
1
x
2
y
0
x
a
b
Рис. 1.3
y
0
x
a
b
Рис. 1.4
Окрестностью первого порядка или слабой окрестностью
)(
*
xy
называется
множество кусочно-гладких функций сравнения
)(xy
таких, что при некотором по-
ложительном числе
ε
имеет место
ε
<
′
−
′
+−
)()()()(
**
xyxyxyxy
,
21
xxx
≤≤
.
Минимум функционала
)(yI
, который достигается на
)(
*
xy
в её сильной (сла-
бой) окрестности, называется сильным (слабым) минимумом функционала
)(yI
.
Аналогично максимум функционала
)(yI
, который достигается на
)(xy
в её сильной
(слабой) окрестности, называется сильным (слабым) максимумом функционала
)(yI
.
Сильный и слабый экстремумы являются относительными экстремумами. Абсолют-
ным экстремумом функционала
)(yI
называется экстремум функционала, который
найден по всей совокупности функций, на которых значение
функционала определено. Абсолютный экстремум функционала
является в то же время относительным.
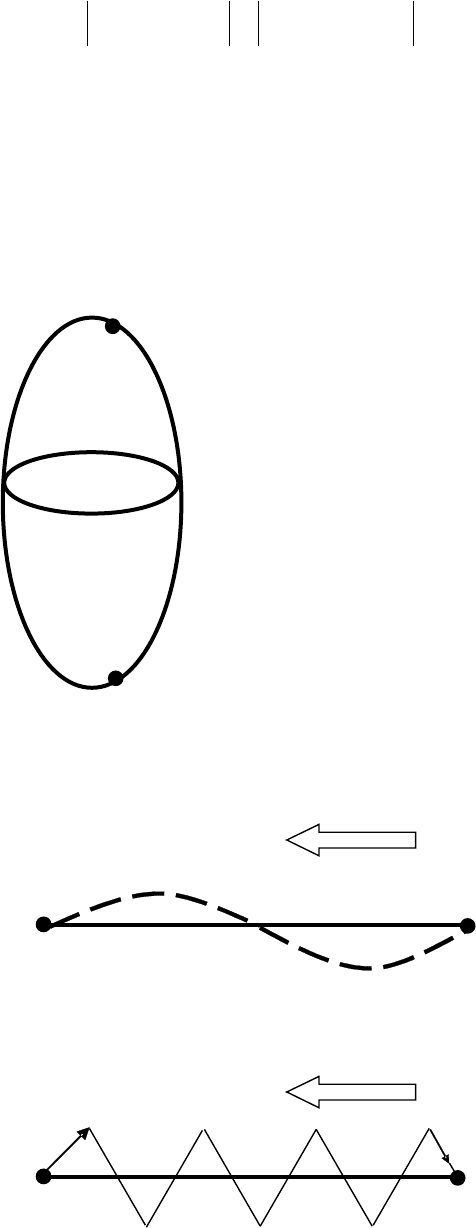
Понятия абсолютного и относительно экстремума функцио-
нала можно проиллюстрировать следующим примером. Требует-
ся найти кратчайший путь между пунктами
A
и
B
(рис. 1.5), раз-
деленным непроходимым препятствием (озеро, гора, лесной мас-
сив и т. п.). Имеется множество путей, огибающих препятствие
слева (справа), есть кратчайший путь. Допустим, что путь справа
короче пути слева. В этом случае абсолютный минимум функцио-
нала, в качестве которого выбрано расстояние между пунктами,
достигается на кратчайшем пути, огибающем препятствие справа.
Относительный минимум достигается на кратчайшем пути, огиба-
ющем препятствие слева, так как этот путь короче других путей,
огибающих препятствие слева.
Понятие сильного и слабого экс-
тремума удобно пояснить следую-
щим примером. Рассмотрим ситуа-
цию, в которой парусно-весельная
лодка движется по озеру навстречу
ветру из пункта
A
в пункт
B
. Пред-
полагается, что скорость движения
под парусами выше скорости движе-
ния на вёслах, но прямо против ветра
двигаться под парусами невозможно.
В этом примере на прямой
AB
до-
стигается сильный минимум функци-
онала, в качестве которого выбрано
время перемещения лодки из пункта
A
в
B
. Любая траектория движения
5
A
B
Рис. 1.5
Ветер
A
B
Рис. 1.6.
Ветер
A
B
Рис. 1.7.
лодки на вёслах лежит в окрестности первого порядка (например, штриховая линия на
рис. 1. 6) увеличивает время пути, хотя расстояние первого порядка от прямой
AB
мало. Время движения между пунктами
A
и
B
можно сократить по сравнению с дви-
жением лодки по прямой
AB
, если двигаться под парусами, короткими галсами (рис.
1.7) в окрестности нулевого порядка от прямой
AB
. таким образом, на прямой
AB
в
рассматриваемом примере сильный минимум функционала не достигается. Отметим,
что всякий сильный экстремум функционала является в то время и слабым функцио-
налом, так как для сильного экстремума сравнение выполняется с кривыми, которые
находятся в близости нулевого порядка, а для слабого сравнение производится с ещё
более узким классом кривых, которые находятся в окрестности первого порядка от
исследуемой функции.
6
2.НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИОНАЛА
Рассмотрим простейшую задачу вариационного исчисления. Требуется найти
минимум функционала
∫
′
=
2
1
12
x
x
dxyyxFyI ),,()().(
среди кусочно-гладких линий, которые соединяют точки
),(
11
yxA
и
),(
22
yxB
, т.е.
,)(
11
yxy
=
,)(
22
yxy
=
21
xxx
≤≤
.
Обычно предполагается непрерывность подынтегральной функции по совокуп-
ности её аргументов, а также существование и непрерывность всех её частных произ-
водных до третьего порядка включительно.
Определим условия, которым должна удовлетворять функция
)(xy
, которая до-
ставляет слабый относительный минимум функционалу (2.10). Необходимые условия
слабого минимума будут тем более необходимыми условиями сильного и абсолютно-
го минимумов.
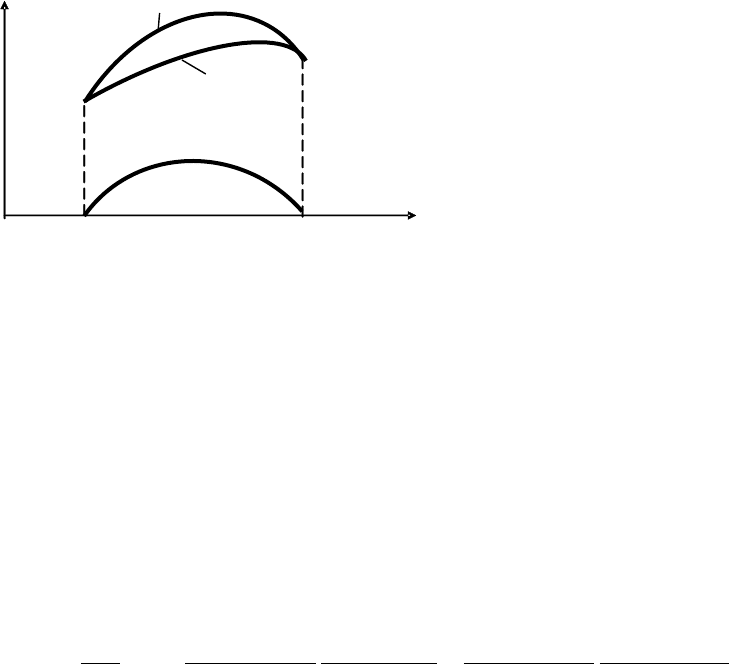
Изменим вид функции
)(xy
путём
прибавки к ней произвольной кусоч-
но-гладкой функции, помноженной на ма-
лый параметр
α
, т.е. получим уравнение
варьируемой кривой (рис. 2.1) в виде
)()()(
~
).( xxyxy
α η
+=
22
.
Если произвольная кусочно-гладкая
функция
)(x
η
удовлетворяет условиям
0
21
==
)()( xx
ηη
, то однопараметриче-
ское семейство функций (2.2) при достаточно малых значениях параметра принадле-
жит некоторой окрестности первого порядка функции
)(xy
.
Функционал
)
~
(yI
на семействе функций
y
~
является функцией параметра
α
:
∫
′
+
′
+==
2
1
32
x
x
dxyyxFФyI ),,()()
~
().(
ηαα ηα
.
Дифференцируя дважды функционал (3.3) по параметру
α
, имеем
=
′
+
′
′
∂
′
∂
+
+
∂
′
∂
=
∫
2
1
Ф
42
x
x
dx
d
yd
y
yyxF
d
yd
y
yyxF
d
d
α
ηα
α
α η
α
)()
~
,
~
,()()
~
,
~
,(
).(
x
y
y(x)
)(
~
xy
η
(x)
x
1
x
2
Рис. 2.1
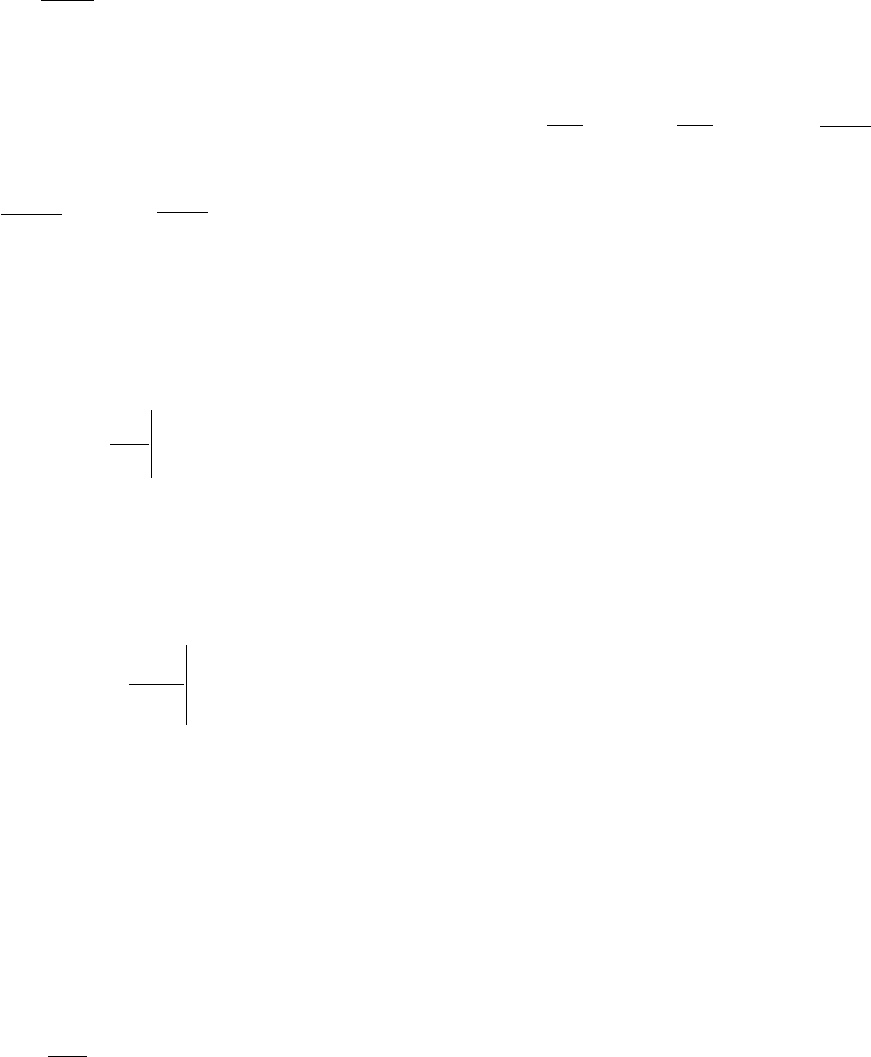
( )
∫
′′
+
′
=
′
2
1
x
x
yy
dxyyxFyyxF ))
~
,
~
,(
~
,
~
,(
ηη
,
( )
∫
′
+
′′
+
′′
=
′′′
2
1
22
2
2
2 52
x
x
yyyyyy
dxyyxFyyxFyyxF
d
Фd
ηηηη
α
)
~
,
~
,()
~
,
~
,()
~
,
~
,().(
,
где введены обозначения частных производных:
;
y
F
F
y
∂
∂
=
;
y
F
F
y
′
∂
∂
=
′
;
2
2
y
F
F
yy
′
∂
∂
=
′′
;
yy
F
F
yy
′
∂∂
∂
=
′
2
.
2
2
y
F
F
yy
∂
∂
=
Первой вариацией функционала
I
δ
называется производная от
)()(
α ηα
+=
yIФ
по параметру
α
в точке
0
=
α
, т.е.
0
Ф
62
=
=
α
α
δ
d
d
I).(
.
Второй вариацией функционала
I
2
δ
называется вторая производная (2.5) от
)()(
α ηα
+=
yIФ
по параметру
α
в точке
0
=
α
, т.е.
0
2
2
2
Ф
72
=
=
α
α
δ
d
d
I).(
.
Необходимым условием экстремума функционала
)(yI
является равенство
нулю его первой вариации (2.6). В случае минимума функционала его вторая произ-
водная (2.7) должна быть неотрицательной:
0
2
≥
I
δ
, а в случае максимума – неполо-
жительной:
0
2
≤
I
δ
.
С целью получения необходимого условия экстремума функционала в форме
уравнения Эйлера первую вариацию функционала
I
δ
приравняем нулю при
0
=
α
.
Тогда выражение (2.4) примет вид
.)),,(),,(()().( 00
Ф
82
2
1
=
′′
+
′
=
∫
′
x
x
yy
dxyyxFyyxF
d
d
ηη
α
Интегрируем по частям второй член выражения (2.8):
8

.).(
∫∫
′′′
−=
′
2
1
2
1
2
1
92
x
x
y
x
x
y
x
x
y
dxF
dx
d
FdxF
ηηη
Учитывая, что произвольная функция
)(x
η
в точках
1
x
и
2
x
обращается в нуль,
т.е.
0
21
==
)()( xx
ηη
, выражение (2.9) запишем в виде
.).(
∫∫
′′
−=
′
2
1
2
1
102
x
x
y
x
x
y
dxF
dx
d
dxF
ηη
Необходимое условие экстремума функционала (2.8) с учётом соотношения
(2.10) получим в форме
.).( 0 112
2
1
=
−
∫
′
x
x
yy
dxF
dx
d
F
η
К этому выражению применим лемму Лагранжа, согласно которой, если непре-
рывная функция
)(xM
обладает тем свойством, что
0
2
1
=
∫
x
x
dxxxM )()(
η
для любой гладкой функции
)(x
η
, то обязательно имеет место
0
=
)(xM
для всех
)(
21
xxxx
≤≤
.
На основании леммы Лагранжа необходимое условие экстремума функционала
(2.11) можно записать в форме уравнения Эйлера
.).( 0 122
=−
′
yy
F
dx
d
F
Гладкое решение уравнения Эйлера называется экстремалью.
Уравнение (2.12) можно представить в другой форме. Выполним полное диффе-
ренцирование по
x
второго члена уравнения Эйлера
dx
yd
y
F
dx
dy
y
F
dx
dx
x
F
F
dx
d
yyy
y
′
′
∂
∂
+
∂
∂
+
∂
∂
=
′′′
′
132 ).(
.
Подстановка (2.13) в (2.12) даёт уравнение Эйлера в виде нелинейного диффе-
ренциального уравнения второго порядка
0 142
=−+
′
+
′′
′′′′
yxyyyyy
FFyFyF).(
.
В общем случае решение уравнения Эйлера вызывает определенные трудности.
Кроме того, экстремали в некоторых случаях могут не доставлять ни максимума, ни
9

минимума функционалу, так как уравнение Эйлера является только необходимым
условием экстремума. Если уравнение не выполняется ни для одной функции, то это
значит, что для данного функционала не существует экстремума в классе кусоч-
но-гладких функций.
Кроме уравнения Эйлера имеется второе необходимое условие экстремума
функционала – условие Лежандра, которое позволяет различать максимум и минимум
функционала. Условие Лежандра выводится из рассмотрения второй вариации функ-
ционала (2.5).
Интегрируя по частям второй член в выражении (2.5), получаем
=−==
′
∫∫∫
′′′′
2
1
2
1
2
1
2
1
222
2 152
x
x
yy
x
x
yy
x
x
yy
x
x
yy
dxF
dx
d
FdFdxF
ηηηηη
).(
∫
′
−=
2
1
2
x
x
yy
dxF
dx
d
η
,
так как
0
21
==
)()( xx
ηη
. С учётом соотношения (2.15) выражение (2.5) принимает
вид
∫
′
+
−=
′′′
2
1
22
2
Ф
162
x
x
yyyyyy
dxFF
dx
d
F
d
d
ηη
α
).(
.
Выберем произвольную функцию
)(x
η
, достаточно малую по абсолютной ве-
личине, но быстро изменяющуюся по
x
. В этом случае знак второй вариации совпа-
дает со знаком
yy
F
′′
, так как
2
η
мало, а
2
η
′
довольно велико.
Ранее указывалось, что в случае минимума функционала вторая вариация (2.16)
должна быть неотрицательной:
0
2
≥
I
δ
, а в случае максимума – неположительной:
0
2
≤
I
δ
.
Итак, второе необходимое условие экстремума – условие Лежандра – формули-
руется следующим образом. Для того чтобы функция
)(xy
доставляла минимум
функционалу
∫
′
=
2
1
x
x
dxyyxFI ),,(
,
должно выполняться неравенство
0
≥
′′
yy
F
, а в случае максимума функционала – не-
равенство
0
≤
′′
yy
F
. В точках экстремали, в которых
0
=
′′
yy
F
, возможны изломы.
Случай вырожденного функционала имеет место, если
yy
F
′′
равно нулю тождествен-
но.
10
