Куцый Н.Н. Теория оптимального управления
Подождите немного. Документ загружается.


9.ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Задачи оптимизации связанные с оптимальным управлением процессами или
объектами различной физической природы (например, электрической, механической,
химической и т.п.), являются весьма важными для приложения в различных областях
техники и промышленности.
Состояние физического процесса или объекта характеризуется переменными со-
стояния (фазовыми координатами)
),(),( txtx
21
,
)(tx
n
. Физический процесс или
динамика объекта описывается системой дифференциальных уравнений (уравнения-
ми состояния), например:
),,,;,,,().(
nni
i
uuuxxxf
dt
dx
2121
19
=
),)(( ni 11
=
где
−
i
u
переменные управления;
−
t
время.
Переменными состояния в электротехнике обычно являются электрические токи
и напряжения, в механике – координаты, скорости и ускорения, в химии – концентра-
ции веществ. Свободные переменные
i
u
позволяют ставить задачу оптимального
управления, т.е. наилучшем (оптимальном) в смысле заданного критерия выборе
переменных управления.
Задача оптимального управления заключается в определении переменных управ-
ления
)(tuu
ii
=
))(( ni 11
=
в интервале
к0
ttt
≤≤
, которые обеспечивают экстремум
(максимум или минимум) критерия качества, заданного в виде функционала
∫
=
к
0
2121к
29
t
t
nn
dtuuuxxxGtP ),,,;,,,()().(
,
и удовлетворяют ограничениям, например
0 39
21
≤
),,,().(
nj
uuuQ
))(( Nj 11
=
,
определяющим замкнутую область допустимых управлений
u
. Примерами кри-
териев качества являются энергетические затраты, время достижения цели, ошибка
управления, стоимость и т.п.
Оптимальное управление
)(tu
i
определяет оптимальную траекторию
)(txx
ii
=
в
−
n
мерном фазовом пространстве, движение по которой из начального состояния в
конечное обеспечивает достижение оптимального значения функционала (критерия
качества.
Решение задачи оптимального управления требует задания начальных
)(
0
tx
i
и
конечных
)(
к
tx
i
состояний. Во многих задачах управления начальное состояние

))(,),(),((
00201
txtxtx
n
задаётся в виде
−−
)(
0
nn
мерного многообразия начальных
состояний (гиперповерхность, линия или точка в пространстве состояний)
0 49
21
=
))(,),(),(().( txtxtxA
nj
))(( nnj
≤=
0
11
.
Таким же образом может быть задано конечное значение
))(,),(),((
кк2к1
txtxtx
n
в виде
−−
)(
к
nn
мерного многообразия конечных состоя-
ний
0 59
21
=
))(,),(),(().( txtxtxB
nj
))(( nnj
≤=
к
11
.
Ряд задач оптимального управления может быть сведён к рассмотренной задаче.
Например, задача оптимального управления с функционалом вида
)),(,),(),((),,,;,,,()().(
кк2к12121к
к
0
69 txtxtxHdtuuuxxxFtP
n
t
t
nn
+=
∫
где
−
H
функция конечного состояния, приводится к задачам с функционалом
(9.2.), т.е.
∫
=
к
0
2121к
t
t
nn
dtuuuxxxGtP ),,,;,,,()(
,
следующим образом:
)()(),,,;,,,().(
02121
79 tHtHFuuuxxxG
nn
−+=
,
где
∑
=
∂
∂
≡≡
n
i
i
i
n
f
x
H
txtxtxH
dt
d
tH
1
21
))(,),(),(()(
.
Нестационарные (неавтономные) задачи (системы), когда одна или несколько за-
данных функций
i
f
и
j
Q
явно зависят от времени
t
(независимой переменной), сво-
дится к рассмотренной задаче путём введения новой переменной состояния
1
+
=
n
xt
,
где
1
1
1 89
+
+
≡=
n
n
f
dt
dx
).(
,
001
ttx
n
=
+
)(
,
кк1
ttx
n
=
+
)(
.
В задачах оптимального управления, в которых ограничения (9.3), т.е.
0
21
≤
),,,(
nj
uuuQ
42
))(( Nj 11
=
,
на переменные управления
i
u
явно зависят от переменных состояния
i
x
(с
учётом и зависимости от
1
+
=
n
xt
), методом введения новых переменных управления
эту зависимость можно исключить. Например, ограничение вида
),,,().(
ni
xxxqu
21
99
≤
путём введения новой переменной управления
v
таким образом, что
),,,().(
ni
xxxvqu
21
109
=
,
приводится к
1 119
≤
v).(
.
Задачу оптимального управления можно рассматривать как вариационную зада-
чу на условный экстремум, например как задачу Лагранжа, Майера или Больца. Одна-
ко применение вариационных методов к задачам оптимального управления встречает
определенные трудности, так как задачи оптимального управления встречает опреде-
ленные трудности, так как задачи оптимального управления содержат ряд особенно-
стей, не учитываемых в вариационных задачах. Задачи оптимального управления по
сравнению с вариационными задачами на условный экстремум имеют следующие
особенности. Во-первых, значения управления
u
, которое рассматривается как одна
из неизвестных функций, принадлежат замкнутому множеству
U
, например, вектор
управления может быть ограничен условием
1
≤
)(tu
. Во-вторых, подынтегральное
выражение функционала и уравнения движения, которые рассматриваются как урав-
нения связи, не зависят от производной управления
u
′
, что приводит к вырожденно-
му виду одного из уравнений Эйлера, которое в этом случае не будет дифференциаль-
ным. В-третьих, в вариационных задачах необходимые условия минимума функцио-
нала выведены в предположении, что неизвестные функции принадлежат классу два-
жды дифференцируемых функций, а в задаче оптимального управления рассматрива-
ется более широкий класс кусочно-непрерывных функций. В задачах оптимального
управления экстремум функционала часто достигается на управлении
)(tu
, которое
имеет точки разрыва первого рода, что в силу уравнений движения приводит к на-
личию точек разрыва производной оптимальной траектории, а положение и число то-
чек разрыва заранее неизвестны.
Оптимальное управление может рассматриваться как обобщенное вариационное
исчисление. Все задачи вариационного исчисления, связанные с максимизацией или
минимизацией интегралов
∫
′′′
=
1
0
2121
129
x
x
nn
dxxxyxyxyxyxyxyGP ));(,),(),();(,),(),(().(
43

при соответствующих ограничениях и граничных условиях, могут быть сформу-
лированы как задачи оптимального управления, если произвести замену
.
),,,
)()();()(
,,).(
ni
xytu
dt
dx
txxy
txtxtx
ii
i
ii
21(
, 139
кк00
=
′
≡≡≡
≡≡≡
Подстановка соотношений (9.13) в функционал (9.12) сводит задачу вариаци-
онного исчисления к задаче оптимального управления с функционалом
∫
=
к
0
2121к
) 149
t
t
nn
dtuuuxxxGtP ),,,;,,,(().(
где
))(( niu
dt
dx
i
i
11
==
.
Следует отметить, что в задачах оптимального управления обычно на перемен-
ные управления наложены ограничения (9.3), т.е.
0
21
≤
),,,(
nj
uuuQ
))(( Nj 11
=
,
которые вызывают определенные затруднения в случае применения методов
классического вариационного исчисления. Это стимулировало разработку специаль-
ных методов для решения задач оптимального управления, таких, как принцип макси-
мума Понтрягина и динамическое программирование Беллмана.
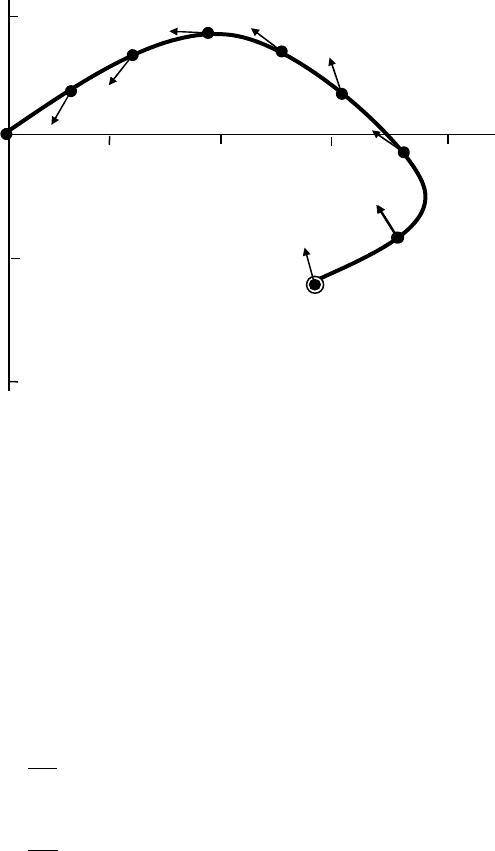
Рассмотрим пример постановки задачи оптимального управления. Кораблю
предстоит проплыть через область сильных течений. Величина и направления скоро-
сти течения задаются, как функции фазовых переменных
),( yxvv
11
=
,
),( yxvv
22
=
,
где
−
yx,
прямоугольные координаты,
−
21
vv ,
компоненты вектора скорости течения
в направлении осей
x
и
y
соответственно (рис. 9.1). Величина скорости корабля от-
носительна постоянна и равна
V
. Уравнения движения корабля имеют вид
44
),,(cos yxvV
dt
dx
1
+=
ψ
),,(sin yxvV
dt
dy
2
+=
ψ
где
−
ψ
угол курса, т.е. угол между осью корабля и фиксированной координат-
ной осью
x
;
−
yx,
координаты корабля.
На рис. 9.1
−
h
масштабная постоянная, стрелками указаны направления оси ко-
рабля, т.е. угол курса
ψ
который в данной задаче является управляющей функцией.
Задача оптимального управления заключается в выборе такого угла курса, при
котором корабль за минимальное время пройдет путь от точки
A
до точки
B
.
Если составляющие скорости течения
1
v
и
2
v
постоянны, то оптимальной траек-
торией движения с минимальным временем будет прямая линия.
45
1
-2
-1
0
1 2
3
4
x/h
Рис. 9.1
y/h

10.ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ
Многие задачи управления, экономики и техники формализуются в виде диффе-
ренциальных игр.
Состояние физического процесса или объекта характеризуется переменными со-
стояния
)(,),(),( txtxtx
n
21
, изменение которых описывается системой обыкновен-
ных дифференциальных уравнений
),,,;,,,;,,,().(
mlni
i
vvvuuuxxxf
dt
dx
212121
110
=
))(( ni 11
=
или векторным дифференциальным уравнением
),,().( vuxf
dt
dx
=
210
,
где
),,,(
n
xxxx
21
=
- точка
−
n
мерного фазового пространства
n
R
, которая
определяет состояние процесса и которая принадлежит области
n
RX
⊂
;
),,,(
l
uuuu
21
=
и
),,,(
m
vvvv
21
=
- управляющие параметры первого и второго
игроков, которые принадлежат соответственно замкнутым ограниченным множе-
ствам
u
E
и
v
E
в евклидовых пространствах
u
R
и
v
R
:
vu
EvEu
∈∈
310 ,).(
;
−=
),,,(
n
ffff
21
действительная вектор-функция, определенная на прямом
произведении
vu
EEX
××
.
Управляющие параметры
)(xu
и
)(xv
, которые выбираются в каждый момент
времени
t
в зависимости от состояния процесса
x
, принято называть стратегиями иг-
роков. Стратегии игроков
)(xu
и
)(xv
определены на
X
, принимают значения соот-
ветственно из
u
E
и
v
E
и обычно выбираются из условия оптимизации некоторого
критерия, который называется платой.
Решение системы обыкновенных дифференциальных уравнений (10.1) при вы-
бранных стратегиях
)(xu
и
)(xv
с начальными условиями
00
xtx
=
)(
, где
−
0
t
мо-
мент начала игры, называется траекторией или партией, которая начинается в точке
0
x
и обозначается как
)](),(,,[ xvxutxx
0
. Развитие игры происходит в области
X
, ко-
торой принадлежат все траектории. игра считается оконченной, когда точка
x
дости-
гает терминального многообразия
M
.
Плата может быть задана для широкого класса игр в форме
)]([),,()](),(,[).( txSdtvuxGxvxuxP
t
t
k0
k
0
410
+=
∫
,
где
−
G
заданная функция, определенная на
vu
EEX
××
;
)]([ txS
k
- функция ко-
нечного состояния, определенная на терминальном многообразии
M
. Интегрирова-
ние производится вдоль траектории от момента начала игры
0
t
до момента оконча-
ния , соответствующего моменту достижения точкой
x
терминального многообразия
M
. В случае
0
k
=
)]([ txS
плата
P
называется интегральной, а при
0
=
G
- терми-
нальной.
Обычно в дифференциальных играх цели игроков считаются противоположны-
ми, а в качестве выбора стратегий
)(xu
и
)(xv
принимают принцип минимакса, т.е.
первый игрок формирует стратегию
)(xu
, минимизирующую плату
P
при условии
максимизации платы вторым игроком
)](),(,[maxmin
)(
)(
xvxuxP
v
u
Exv
Exu
0
∈
∈
,
а второй игрок формирует стратегию
)(xv
, максимизирующую плату при усло-
вии минимизации платы первым игроком
)](),(,[minmax
)(
)(
xvxuxP
u
v
Exu
Exv
0
∈
∈
.
Стратегии
)(xu
0
и
)(xv
0
называются оптимальными, если выполняется соотно-
шение
)](),(,[maxmin
)(
)(
xvxuxP
v
u
Exv
Exu
0
∈
∈
=
)](),(,[minmax
)(
)(
xvxuxP
u
v
Exu
Exv
0
∈
∈
=
=
)](),(,[ xvxuxP
000
.
Выполнение этого условия свидетельствует о наличии седловой точки игры, ко-
торая обладает тем свойством, что любое отклонение от оптимальной стратегии од-
ним игроком приводит к потерям в плате при условии выбора оптимальной стратегии
другим игроком
≥
)](),(,[ xvxuxP
00
)](),(,[min
)(
xvxuxP
u
Exu
00
∈
,
≤
)](),(,[ xvxuxP
000
)](),(,[max
)(
xvxuxP
v
Exv
00
∈
.
Плата
)](),(,[ xvxuxP
000
, соответствующая оптимальным стратегиям
)(xu
0
и
)(xv
0
, называется ценой игры.
Основная задача дифференциальных игр заключается в определении цены игры,
оптимальных стратегий игроков и траекторий, соответствующих оптимальным стра-
тегиям. Данная постановка задачи относится к классу дифференциальных игр двух
игроков с нулевой суммой, когда выигрыш одного игрока равен проигрышу другого.
Дифференциальные игры являются наиболее общим классом оптимизационных за-
дач. Например, задачи оптимального управления могут рассматриваться как частный
случай дифференциальной игры с одним игроком. Это утверждение следует из непо-
средственного сравнения постановок задачи оптимального управления (9.1),(9.2), т.е.
47
),,,;,,,(
nni
i
uuuxxxf
dt
dx
2121
=
),)(( ni 11
=
∫
=
к
0
2121к
t
t
nn
dtuuuxxxGtP ),,,;,,,()(
и дифференциальной игры (10.1), т.е.
),,,;,,,;,,,(
mlni
i
vvvuuuxxxf
dt
dx
212121
=
))(( ni 11
=
,
из которой исключаются управляющие параметры второго игрока. если учесть,
что задачи оптимального управления, как показано выше, могут рассматриваться как
обобщенное вариационное исчисление, то между дифференциальными играми, опти-
мальным управлением и вариационными задачами существует связь в отношении их
математических моделей.
Дифференциальные игры являются наиболее универсальной моделью динами-
ческих оптимизационных задач, которые требуют применения наиболее сложных ме-
тодов и средств моделирования.
На примере задачи перехода корабля из заданного начального состояния в ко-
нечное за минимальное время, которая рассматривалась выше, покажем связь задач
оптимального управления и дифференциальных игр. Если о компонентах вектора
скорости течения ничего неизвестно, кроме ограничений
m
vv
11
≤
,
m
vv
22
≤
, где
m
v
1
и
m
v
2
- известные граничные значений допустимой скорости течения, то задача опти-
мального управления переходит в класс дифференциальных игр. В качестве первого
игрока может рассматриваться судоводитель, выбирающий оптимальный курс кораб-
ля
ψ
, а второй игрок – это неизвестные воздействия
1
v
и
2
v
природных сил в виде
течения, которому можно приписать целенаправленное поведение, максимизирующее
время перехода корабля из начального положения в конечное. Если судоводитель бу-
дет выбирать оптимальный курс корабля из решения дифференциальной игры, то он
гарантирует оптимальный по времени переход корабля в заданную конечную точку
при любом законе изменения скорости течения вдоль траектории движения. Если за-
кон изменения скорости течения известен, то оптимальный курс необходимо выби-
рать из решения задачи оптимального управления.
48

11.МЕТОДЫ РЕШЕНИЯ. ПРЯМЫЕ МЕТОДЫ
Методы вариационного исчисления, основанные на интегрировании уравнений
Эйлера, малоэффективны, так как приводят к трудоёмким вычислениям. Это связано
с тем, что дифференциальные уравнения вариационных задач интегрируются в конеч-
ном виде лишь в исключительных случаях.
Известен ряд приближенных методов решения вариационных задач, среди кото-
рых получили большое распространение для решения прикладных вариационных за-
дач так называемые прямые методы. Сущность прямых методов заключается в том,
что вариационная задача рассматривается как предельная для некоторой задачи на
экстремум функции конечного числа переменных, которая решается обычными мето-
дами.
Действительно, функционал
)]([ xyI
можно рассматривать как функцию беско-
нечного множества переменных, если учесть, что функции
)(xy
могут быть разложе-
ны в бесконечные ряды, например степенные ряды
+++++=
n
n
xaxaxaaxy
2
210
)(
,
в ряды Фурье
( )
∑
∞
=
++=
1
0
2
n
nn
nxbnxa
a
xy sincos)(
или в ряды вида
∑
∞
=
=
0
111
n
nn
xaxy )()().(
ϕ
,
где
−
)(x
n
ϕ
заданные функции.
Чтобы представить функцию
)(xy
в виде ряда (11.1), достаточно задать значе-
ния всех коэффициентов
n
a
. Значение функционала
)]([ xyI
в этом случае определя-
ется заданием бесконечной последовательностью чисел
,,,,,
n
aaaa
210
Таким
образом, функционал является функцией бесконечного множества перемененных
),,,,()]([
n
aaaxyI
10
ϕ
=
. В этом заключается основное различие между вариаци-
онными задачами, в которых ищется экстремум функции бесконечного множества
переменных, и задачами на экстремум функций конечного числа переменных.
Среди прямых методов наибольшее распространение получили конечно-раз-
ностный метод Эйлера, метод Ритца и метод Канторовича.
По методу Эйлера значения функционала
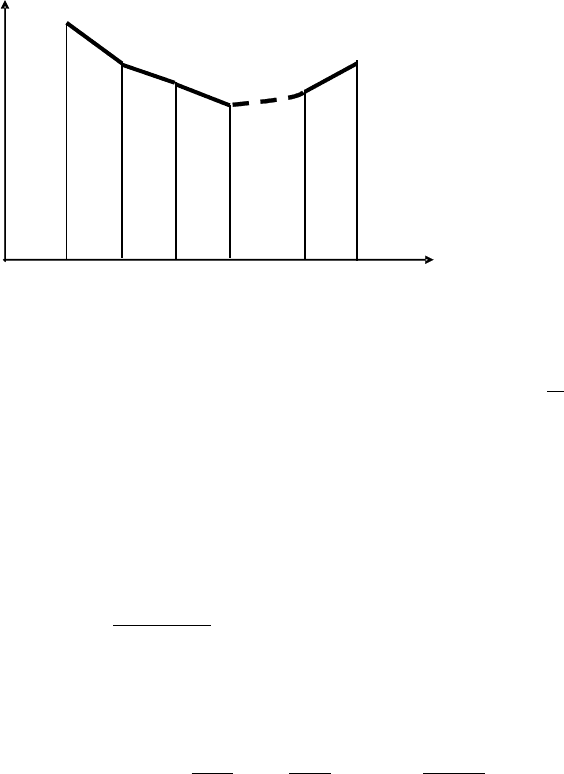
∫
′
=
2
1
211
x
x
dxyyxFI ),,().(
,
axy
=
)(
1
,
bxy
=
)(
2
рассматриваются не на произвольных кривых, а на ломанных (рис.11.1), состав-
ленных из заданного числа
n
прямолинейных звеньев, с заданными абсциссами вер-
шин
xx
∆+
0
,
xx
∆+
2
0
,...,
xnx
∆−+
)( 1
0
, где
)(
0
1
xx
n
x
n
−=∆
. В этом случае функ-
ционал (11.2) превращается в функцию ординат
121
−
n
yyy ,,,
вершин ломаной
∑
=
∆
′
=
n
i
iiin
xyyxFI
0
311 ),,().(
где
x
yy
y
ii
i
∆
−
=
′
+
1
.
Если на ломаной линии достигается экстремум, то все частные производные
должны быть равны нулю:
00 0 411
121
=
∂
∂
=
∂
∂
=
∂
∂
−
n
nnn
y
I
y
I
y
I
,,,).(
.
Ординаты
121
−
n
yyy ,,,
ломаной, которая доставляет экстремум функционалу
(11.3), находим из системы уравнений (11.4). Если затем перейти к пределу при
∞→
n
, то при некоторых ограничениях, налагаемых на функцию
F
, можно полу-
чить решение исходной вариационной задачи (11.2).
Можно показать, что для функционала (11.3) существует дискретный аналог
уравнений Эйлера. Рассмотрение членов суммы (11.3) показывает, что от
i
y
зависят
лишь два слагаемых этой суммы:
i
и
1
−
i
. Причём
i
-й член
),,(
iii
yyxF
′
содержит
i
y
непосредственно и в аргументе
50
y
0
y
1
y
2
y
n-1
y
n
x
0
x
0
+
∆
x
x
n-1
x
n
x
y
Рис. 11.1
