Кубота Н. Твердые ракетные топлива и взрывчатые вещества

Подождите немного. Документ загружается.

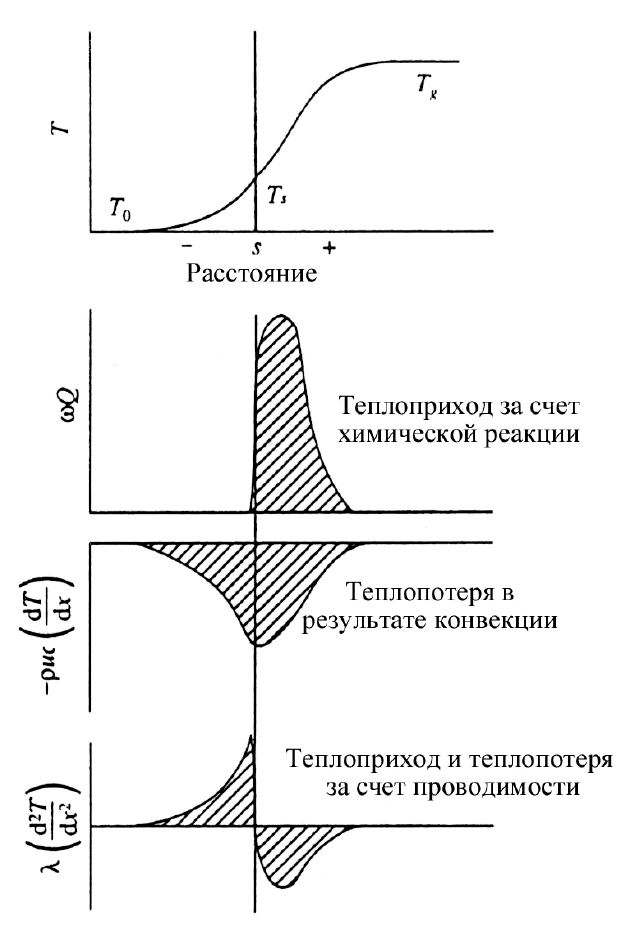
нуля в дальней точке. Теплоперенос в газовую фазу прекращается на значитель-

ном расстоянии от поверхности горения, где температура достигает максимума и

образуются конечные продукты сгорания.

Рис. 3.11. Схематическое представление процессов оттока теплоты

в волну горения

3.5.1.2 Тепловая структура в конденсированной фазе

Для описания процесса энергопереноса в конденсированную фазу сделано

несколько дополнительных допущений в вышеприведенных уравнениях [9, 10]:

(1)

эндотермических или экзотермических реакций не происходит в кон-

денсированной фазе (ниже поверхности горения);

(2)

светящаяся зона пламени не делает вклада в обратную теплопровод-

ность от газовой фазы к поверхности горения;

(3)

не происходит диффузии компонентов в конденсированной или газовой

фазе.

Уравнения (3.39) и (3.40) можно упростить следующим образом:

0=−

⎟

⎠

⎞

⎜

⎝

⎛

ppp

ρλ , (3.43)

=−−

r ω

(3.44)

Интегрирование уравнения (3.43) при граничных условиях:

Т = Т

при x = – ∞;

Т = Т

при x = 0

дает

Т(x) – Т

= (Т

– Т

) еxp (rx/α

), (3.45)

где α

– температуропроводность конденсированной фазы, определяемая как

= λ/ρ

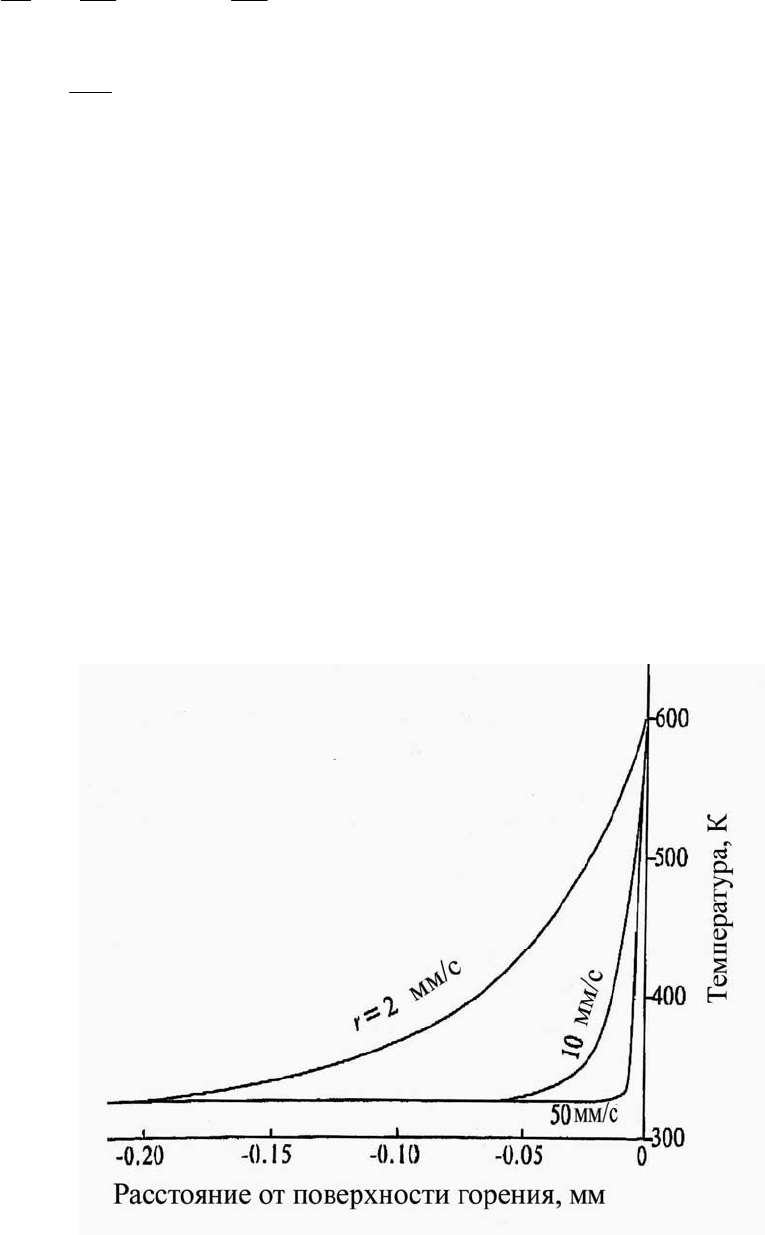
, то есть является независимой от температуры. На рис. 3.12 показаны

температурные профили в конденсированной фазе при r = 2 мм/с, 10 мм/с и

50 мм/с с допущениями, что T

= 325 К, T

= 600 К, λ

= 2,10 × 10

–4

кДж/с⋅м⋅К,

= 1600 кг/м

, с

= 1,47 кДж/кг К и α

= λ

/ρ

= 8,93 × 10

–8

/с. Толщина тепло-

вой волны в конденсированной фазе, определяемая как δ

= α

/r, составляет 45, 9

и 1,8 мк при r = 2, 10, 50 мм/с, соответственно. Температурный градиент в кон-

денсированной фазе увеличивается с увеличением скорости горения, то есть δ

уменьшается с увеличением скорости горения.

Рис. 3.12. Температурный профиль в конденсированной фазе

энергетического материала

3.5.1.3 Термическая структура в газовой фазе

Так как энергетические материалы состоят из нескольких химических ин-

гредиентов и каждая молекулярная структура является сложной, многочисленные

газообразные компоненты образуются на поверхности горения, и схемы их реак-

ций довольно сложны. Таким образом, определение скорости горения в газовой

фазе для каждого из компонентов j в процессе горения является довольно труд-

ным делом

. Трактовка реакции в газовой фазе, которая определяет температурный

градиент выше поверхности горения, Φ= (dТ/dx)

s,g

и обратный поток теплоты из

газовой в конденсированную фазу, Λ

= λ

Φ является отправной точкой, которая

приводит к уравнению скорости горения. Чтобы достичь фундаментального по-

нимания процесса обратного теплопотока в газовой фазе, допустим, что выделе-

ние тепла в газовой фазе задается ступенчатой функцией и имеет положительное

постоянное значение Q

. Модель характеризует обратный тепловой поток из га-

зовой фазы в конденсированную фазу и при интегрировании уравнения (3.41)

принимается граничное условие, что тепловой поток в бесконечности равен нулю:

()

∫

∞

−=Λ

/exp dxxucQ

ggggggg

ωλρ

(3.46a)

По аналогии с конденсированной фазой температуропроводность в газовой

фазе задается как α

= λ

/ρ

, то есть допускается, что она не зависит от темпера-

туры. Толщина тепловой волны в газовой фазе δ

определяется как δ

g =

/и

. Далее

уравнение (3.46а) может быть представлено:

()

∫

∞

=−=Λ

/exp dxxuQ

ggggg

ωα

(3.46b)

()

∫

∞

−

/exp dxxQ

ggg

ωδ

(3.46с)

В общем, скорости реакций сильно зависят от температуры, когда энергия

активации высока. Таким образом, предполагается, что два важнейших фактора,

влияющих на скорость реакции – температура и концентрация реагирующего ве-

щества имеют тенденцию взаимоисключать друг друга, так как реакция протекает

таким образом, что при повышении температуры концентрация реагирующих ве-

ществ уменьшается.

Кроме того, предполагается, что результирующая постоянная

скорость реакции выявлена только в ограниченной зоне, то есть между x = x

x = x

.(рис. 3.13) и что скорость реакции в газовой фазе можно выразить через

ступенчатую функцию. Таким образом, интегрируя уравнение (3.46с), получаем

уравнение

[]

()()

(

)

{

}

gggigggg

xxQ

δδωδ

/exp/exp −−−=Λ , (3.46d)

где [ω

] – константа, имеющая положительное значение для x

< x ≤ x

, а равная

в другом месте равна нулю; [ω

] необходимо рассматривать как среднее значение

в случае реальной скорости реакции, возникающей в газовой фазе.

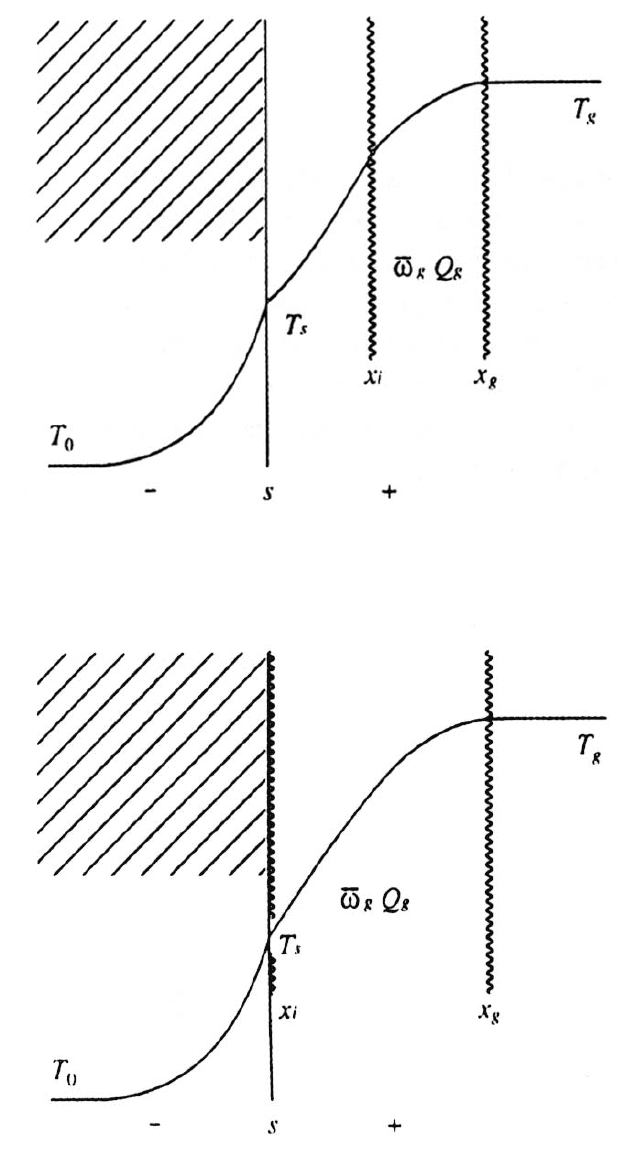
Рис. 3.13. Модель ступенчатой функции для реакции в газовой фазе,

которая начинается при x = x

и заканчивается при x = x

Рис. 3.14. Модель ступенчатой функции для реакции в газовой фазе,

которая начинается при x

= 0 и заканчивается при х = x

Если предположить, что химическая реакция, представленная как ступенча-

тая функция, начиная при x

= 0, то есть на поверхности горения, и заканчивается

при x = x

в газовой фазе, как показано на рис. 3.14, то уравнение (3.46d) можно

переписать следующим образом:

[]

()(){}

gggggg

δωδ

/exp1 −−=Λ (3.47)

Если член в экспоненциальном выражении x

>> 1, то упрощенное выра-

жение для теплового потока в обратном направлении от газовой в твердую фазу

получается [8]:

[ω

(3.48)

Эта асимптота имеет место всякий раз, когда тепло, передаваемое в обрат-

ном направлении к поверхности горения, является небольшим по сравнению с те-

плом, высвобождаемым в газовой фазе, из чего следует, что значение x

/δ

доста-

точно велико. Хотя уравнение (3.48) неточно, оно, однако, характеризует поведе-

ние скорости горения без введения математических сложностей и параметров ре-

акции.

3.5.1.4 Модель скорости горения

Если тепловой поток подается в обратном направлении из зоны II в зону I за

счет теплопроводности, то Λ

можно записать в следующем виде:

= λ

(dТ/dx)

s,р

= ρ

r(Т

– Т

), (3.49)

и тепловой поток, генерируемый в зоне конденсированной фазы на поверхности

горения Г

, равен

= ρ

, (3.50)

где индекс s означает поверхность горения, а р – зону реакции в конденсирован-

ной фазе на поверхности горения. Граничные условия для уравнения энергии в

конденсированной фазе и на поверхности горения, соответственно, задаются сле-

дующим образом:

Т = Т

при x = – ∞

= Λ

+ Г

при x = 0 (3.51)

Обычно скорость ω

одноступенчатой реакции

∑∑

′′

⎯→⎯

′

MvMv

может быть представлена как

()

∏

′

−

′′

===

hggii

kvv

ερ

ρω

, (3.52)

где М – обозначение произвольных химических компонентов, N – число парал-

лельных путей реакций в газовой фазе, k

– константа скорости реакции,

′

–

стехиометрические коэффициенты для компонентов i как реагирующих веществ и

j как продуктов реакции, соответственно. Поэтому обратный тепловой поток из

газовой фазы к поверхности горения получается из уравнений (3.42), (3.48) и

(3.52):

()

∑

∏

′

−

′′

=Λ

hggiiggg

kvvQ

ερδ

(3.53)

Предположим, что коэффициент температуропроводности на поверхности

раздела между конденсированной и газовой фазой, то есть на поверхности горе-

ния, представлен как

gpg

= . Тогда, используя уравнение неразрывности

массы между конденсированной и газовой фазой

ggp

, представленное

уравнением (3.1), определяют толщину тепловой волны δ

как

. Затем,

комбинируя уравнения (3.51) с (3.53) и решая относительно r, получаем

()

⎥

⎦

⎤

⎢

⎣

⎡

′

−

′′

−−

∑

∏

′

hggiig

psspp

kvvQ

cQTTc

ερ

(3.54)

Уравнение (3.54) является упрощенным уравнением для скорости горения.

Если скорости реакции в газовой фазе известны, то скорость горения задается че-

рез плотность газа (давление), температуру поверхности горения, начальную тем-

пературу топлива и физические свойства энергетического материала.

Температура поверхности горения связана со скоростью горения с помощью

уравнения Аррениуса, которое предполагает реакцию разложения

первого поряд-

ка для каждого вида реакционных компонентов на поверхности горения:

()

∑

−=

sjsjsj

RTEZr

/exp

, (3.55)

где K – число предполагаемых параллельных, независимых путей реакций гази-

фикации в конденсированной фазе. Уравнения (3.54) и (3.55) при сочетании могут

дать скорость горения и температуру поверхности горения для заданного ряда ус-

ловий.

Обычно реакции газовой фазы в моделях пламени предварительно переме-

шанных газов и газофазные реакции горения энергетических материалов, как

предполагают, являются

бимолекулярными и, следовательно, второго порядка.

Далее мы можем выразить уравнение (3.54) как

()

{}

(

){}

[]

2/1

pssppgggg

cQTTckQr −−=

ρρεα

(3.56)

Константа скорости реакции k

является функцией температуры и может

быть записана в следующем виде:

= Z

exр(–Е

/RТ

) (3.57)

Закон идеальных газов также может быть использован и связан с предпола-

гаемыми постоянными в пространстве р и Т

= р/R

(3.58)

Уравнения (3.57) и (3.58) при подстановке в уравнение (3.56) дают возмож-

ность получить уравнение для скорости горения для энергетических материалов

топлива при допущениях, приведенных выше:

()

/exp

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

pss

ggggg

cQTT

RTEZQ

, (3.59)

где Т

задается как

= Т

+ Q

/с

+ Q

/с

(3.60)

Скорость разложения на поверхности горения, то есть скорость горения,

может быть выведена из уравнения (3.55):

r = Z

еxр (–Е

/RT

) (3.61)

Нелинейный характер алгебраических уравнений (3.59) и (3. 61) подразуме-

вает необходимость их решения методом итераций.

3.5.2 Расстояние отбрасывания пламени

Если реагирующий газ, образующийся на поверхности горения энергетиче-

ского материала, реагирует медленно в газовой фазе и генерирует светящееся

пламя, то расстояние L

между поверхностью горения и фронтом светящегося

пламени называется расстоянием отбрасывания пламени. В газовой фазе, пока-

занной на рис. 3.9, температурный градиент, по-видимому, является небольшим, и

температура увеличивается относительно медленно. В этом случае тепловой по-

ток, передаваемый теплопроводностью, первый член уравнения (3.41) является

незначительным. Аналогично, скорость массовой диффузии, первый член уравне-

ния (3.42),

как предполагается, является небольшим по сравнению со скоростью

массовой конвекции, вторым членом уравнения (3.42).

Таким образом, получаем:

0=+−

ggggg

cu ωρ , (3.62)

0=−−

(3.63)

Скорость реакции для реакции m-порядка может быть задана (игнорируя

температурную зависимость ρ

()

ggg

RTEZ /exp −=

ρεω

(3.64)

Комбинируя уравнения (3.62) и (3.64), получаем

()

(

)

ggg

gggg

RTEZQuc

/exp/1

−=

−

ρε

(3.65)

Зависимость неразрывности (сплошности) потока массы между газовой фа-

зой и твердым телом можно представить в следующем виде:

= rρ

/ρ

(3.66)

Комбинируя уравнения (3.65) и (3.66) и используя закон идеального газа,

получаем

dT/dx = (1/c

r)Q

)

–m

exp(–E

/RT

) (3.67)

Скорость горения энергетического материала выражается как

r = ap

, (3.68)

где п – показатель степени в законе скорости горения, а – постоянная, завися-

щая от химического состава и начальной температуры топлива. Подставляя урав-

нение (3.68) в уравнение (3.67), получают

()()

(

)

gpg

pRTEZTRQacdxdT

−

−= /exp/1/

ερ

(3.69)

Температурный градиент dТ/dх в газовой фазе приблизительно равен

ΔТ

, где ΔТ

является изменением температуры в зоне газовой фазы. Таким об-

разом, расстояние отбрасывания пламени L

составляет:

()

ggg

gpgg

RTEZQ

RTacT

/exp −

−

, (3.70)

dmn

pp =

−

(3.70а)

3.5.3 Характеристики скорости горения энергетических материалов

3.5.3.1 Показатель степени в законе скорости горения

Обычно скорость горения энергетических материалов увеличивается ли-

нейно по мере увеличения давления при использовании логарифмических коор-

динат для уравнения (3.68) при постоянной начальной температуре Т

, где

r – скорость горения, р – давление. Таким образом, чувствительность к давлению

скорости горения при постоянной начальной температуре n определяется как

⎟

⎠

⎞

⎜

⎝

⎛

∂

= (3.71)

3.5.3.2 Температурная чувствительность скорости горения

Скорость горения любого энергетического материала зависит также от на-

чальной температуры материала, Т

, даже когда давление при горении поддержи-

вается постоянным. Температурная чувствительность скорости горения σ

опре-

деляется изменениями скорости горения при изменении Т

−

, (3.72а)

где r

и r

– скорости горения при Т

и Т

, соответственно, r – средняя скорость

между Т

и Т

. Таким образом, величина σ

, по-видимому, равна K

–1

. Дифференци-

альная форма уравнения (3.72а) записывается в виде

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

ln1

(3.72b)

Используя уравнение (3.68), получаем

(

)

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎥

⎦

⎤

⎢

⎣

⎡

∂

1ln

(3.72c)

Температурная чувствительность скорости горения, определяемая уравне-

нием (3.72a), является параметром значительной уместности энергетических ма-

териалов.

3.5.4 Анализ температурной чувствительности скорости горения

Чтобы понять фундаментальную концепцию причины температурной чув-

ствительности, анализ, проведенный в этом разделе, предполагает, что волна го-

рения гомогенна и состоит из стационарных одномерных последовательных реак-

ционных зон. Реакция в газовой фазе происходит с одноступенчатым температур-

ным подъемом от температуры горящей поверхности до максимальной темпера-

туры пламени. Теплопередача в структуре волны

горения энергетических мате-

риалов показана на рис. 3.10. Обратный тепловой поток из зоны III в зону II за

счет теплопроводности Λ

= λ

(dТ/dx)

s,g

задан уравнением (3.46), а обратный теп-

ловой поток из зоны II в зону I за счет теплопроводности, Λ

= λ

(dТ/dx)

s,р

задается

уравнением (3.49). Используя интегрированное уравнение энергии [уравнение

(3.51)] на поверхности горения, скорость горения можно представить так:

Φ=

(3.73)

Φ = (dТ/dx)

s,g

(3.74)

ϕ = Т

– Т

– Q

/с

(3.75)

, (3.76)

где α

– коэффициент температуропроводности на поверхности горения.

Уравнение (3.73) показывает, что скорость горения энергетических мате-

риалов определяется двумя параметрами: газофазный параметр Ф , который опре-

деляется физическими и химическими свойствами газовой фазы, а параметр кон-

денсированной фазы φ, который определяется физическими и химическими свой-

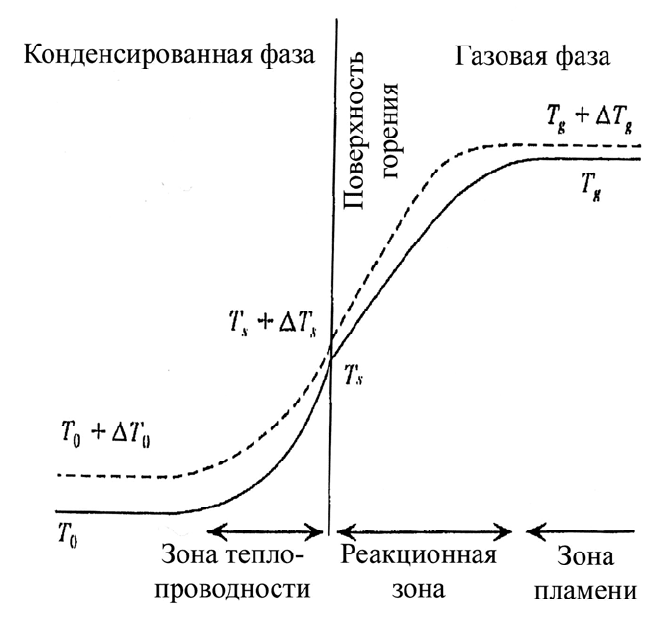
ствами конденсированной фазы. Когда начальная температура увеличивается от

до Т

+ ΔТ

, то температурный профиль соответствует представленному на

рис. 3.15. Температура горящей поверхности Т

также увеличивается до значения

+ ΔТ

, и конечная температура горения увеличивается с Т

до Т

+ ΔТ

Рис. 3.15. Температурные профили в волне горения при различных начальных

температурах энергетического материала

Когда логарифмическая форма уравнения скорости горения, заданная урав-

нением (3.73), дифференцируется относительно начальной температуры энерге-

тического материала при постоянном давлении, то получается следующее выра-

жение:

() ()

{

}

(

)

{

}

psspp

TcQTTcdTdxdTTr

000

//ln//ln/ln ∂−−∂−∂=∂∂

ρλ

(3.77)

Следовательно, физическое свойство α

– температуропроводность на горя-

щей поверхности не зависит от Т

и уравнение (3.77) записывается:

()()

∂

∂−∂Φ∂=

рр

TТ

/ln/ln

, (3.78)

где

()

/ln ∂Φ∂=Φ (3.79)

()

/ln ∂∂−=Ψ

(3.80)

Из уравнения (3.78) видно, что температурная чувствительность состоит из

двух параметров [11] Φ и Ψ: Φ – так называемая "температурная чувствитель-

ность газовой фазы", которая определяется параметрами газовой фазы, и

Ψ – так называемая "температурная чувствительность конденсированной фазы",

которая определяется параметрами конденсированной фазы.

Если предположим, что реакция в газовой фазе записывается уравнением

(3.48), то

обратный тепловой поток от газовой фазы к горящей поверхности опре-

деляют как

Φ = α

[ω

/r (3.81)