Кубота Н. Твердые ракетные топлива и взрывчатые вещества

11

Изменения температуры, давления и плотности в поле течения выражаются

как функции числа Маха:

2

0

2

1

1 М

T

T −

+=

γ

, (1.25)

1

2

0

2

1

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+=

γ

M

p

, (1.26)

1

2

0

2

1

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+=

γ

ρ

M (1.27)

1.2.2 Образование ударной волны

Предположим, что имеет место прерывное течение между областями 1 и 2,

как показано на рис. 1.2. Также предполагается, что имеет место одномерное ста-

ционарное течение без вязких внешних сил и химических реакций.

Уравнение сохранения массы записывается в виде:

ρ

1

u

1

= ρ

2

u

2

= m (1.28)

Уравнение сохранение количества движения записываем в виде

p

1

+ mu

1

2

= p

2

+mu

2

(1.29)

Уравнение сохранения энергии представлено с использованием уравнения

(1.20):

2

1

22

u

Tc

u

Tc

pp

+=+ , (1.30)

где обозначения 1 и 2 означают вход и выход потока. Подставляя уравнение (1.28)

в уравнение (1.29), получаем:

2

222

2

111

upup

ρρ

+=+ (1.31)

1 2

p

1

p

2

ρ

1

ρ

2

T

1

T

2

u

1

u

2

M

1

M

2

Ударная волна

Рис. 1.2. Распространение ударной волны

Используя уравнение (1.25), можно представить отношение температур в

зонах 2 и 1 через число Маха в этих зонах:

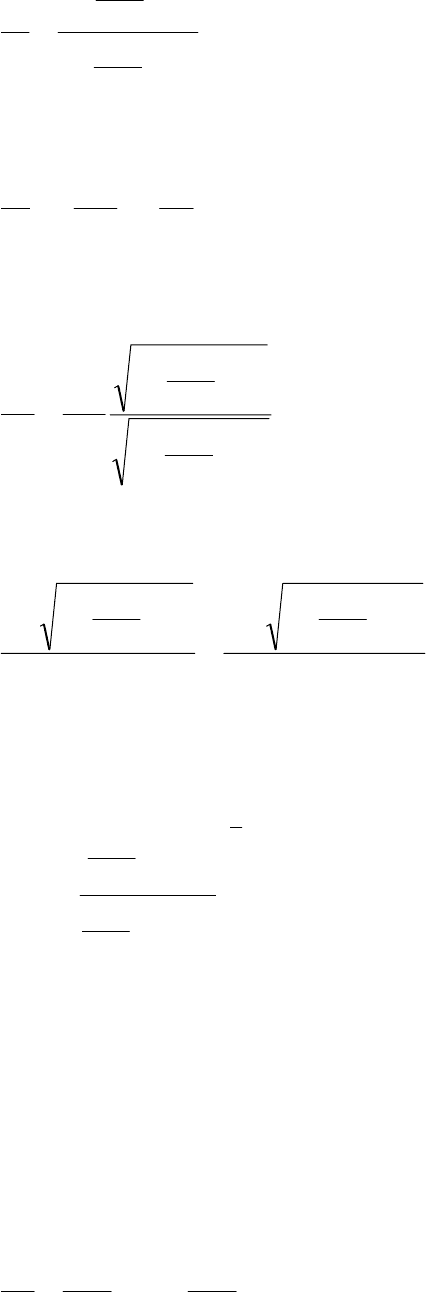
12

2

1

2

1

2

1

M

T

−

+

−

+

=

γ

(1.32)

Используя уравнения (1.5), (1.17) и (1.28), получаем:

2

1

2

1

2

1

2

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=

p

M

T

(1.33)

Комбинируя уравнения (1.33) и (1.32), получаем отношение давлений как

функцию

М

1

и М

2

:

2

1

2

1

2

1

2

1

M

p

−

+

−

+

=

γ

(1.34)

Комбинируя уравнения (1.16), (1.17) и (1.34), можно получить зависимость

чисел Маха на входе и выходе:

2

22

2

1

2

11

1

2

1

2

1

M

MM

M

MM

γ

+

−

+

=

+

−

+

(1.35)

Из уравнения (1.35) получаются два решения:

М

2

= М

1

(1.36)

2

1

2

1

2

1

2

1

2

1

2

⎥

⎦

⎤

⎢

⎣

⎡

−

+

−

=

M

γ

(1.37)

Из решения уравнения (1.36) очевидно, что непрерывное течение происхо-

дит из области 1 в область 2. Однако решение уравнения (1.37) указывает на су-

ществование отсутствия непрерывности давления, плотности и температуры меж-

ду областями 1 и 2. Этот разрыв называется "нормальной ударной волной", кото-

рая присутствует в поле течения и распространяется перпендикулярно направле-

нию течения. Обсуждения структур

нормальных ударных волн и сверхзвуковых

полей течения приведены в работах [4] и [5]. Подставляя уравнение (1.37) в урав-

нение (1.34), получаем соотношение давлений:

1

2

1

2

+

−

+

=

γ

M

p

(1.38)

Подставляя уравнение (1.37) в уравнение (1.33), получаем отношение тем-

ператур:

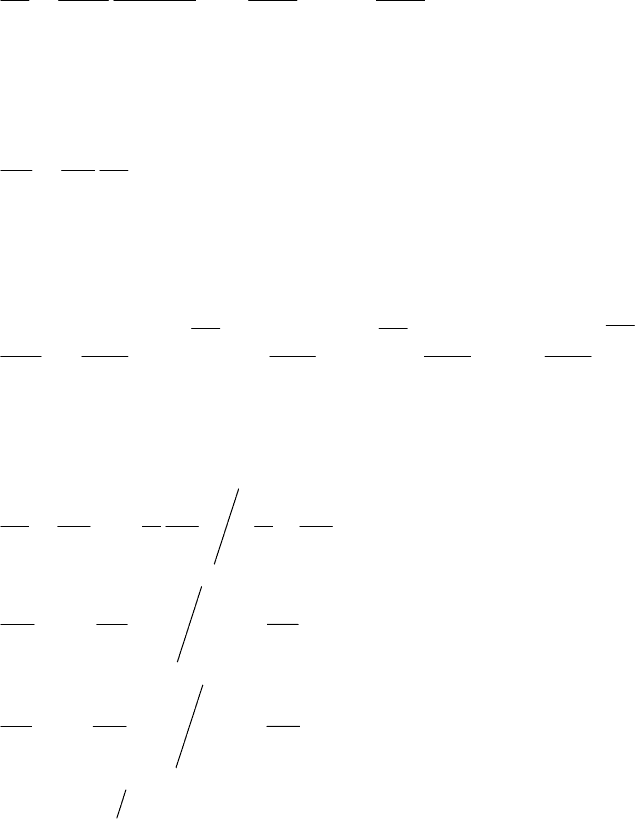
13

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+

−

= 1

1

2

1

)1(

)1(21

2

1

2

1

22

1

2

MM

M

T

γ

γγ

γ

(1.39)

Соотношение плотностей получается с использованием уравнений (1.38),

(1.39) и (1.8):

2

1

2

1

2

T

p

=

ρ

(1.40)

Используя уравнение (1.24) для входящего и выходящего потока и уравне-

ние (1.38), получаем отношение давлений стагнации:

γ

γγγ

−

−−

⎟

⎠

⎞

⎜

⎝

⎛

+

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−

+

⎟

⎠

⎞

⎜

⎝

⎛

+

=

1

2

1

2

1

2

1

01

02

1

2

1

2

1

MMM

p

(1.41)

Отношения температур, давлений и плотностей до входа и на выходе выра-

жаются следующими зависимостями:

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

+=

1

2

1

2

1

2

1

2

11

1

p

T

ζζ

, (1.42)

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−=

1

2

1

2

1

2

1

ρ

ζ

ρ

ζ

p

, (1.43)

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

+=

1

2

1

2

1

2

1

p

ζζ

ρ

,

(1.44)

где

()()

11 −+=

γ

ζ

. Система уравнений (1.42), (1.43) и (1.44) известна как

уравнение Ренкина-Гюгоньо для ударной волны без учета химических реакций.

Зависимость

p

2

/p

1

и ρ

2

/ρ

1

при γ=1,4 (например, в случае воздуха) показывает, что

давление на выходе увеличивается бесконечно, тогда как плотность выходящего

потока увеличивается приблизительно в 6 раз. Это очевидно из уравнения (1.43),

когда ,/

12

ζ

ρ

→ тогда

∞

→

12

/ pp .

Хотя система уравнений Ренкина-Гюгоньо (1.42) – (1.44) получается, когда

стационарная ударная волна создается в движущейся системе координат, то та же

самая зависимость получается для движущейся ударной волны в неподвижной

системе координат.

В неподвижной системе координат скорость движущейся ударной волны

составляет u

1

и скорость частицы u

p

тогда записывается как

21

uuu

p

−= .

Отношения температур, давлений и плотностей являются одними и теми же

для движущейся и неподвижной системы координат. Изменение энтропии попе-

рек ударной волны характеризует ударную волну. Используя уравнение состояния

для идеального газа (уравнение 1.5), можно получить изменение энтропии:

() ( )

121212

/ln/ln ppRTTcss

gp

−=− (1.45)

14

Подставляя уравнения (1.38) и (1.39) в уравнение (1.45), получаем:

()

⎥

⎦

⎤

⎢

⎣

⎡

ζ

−

+γ

γ

+

⎥

⎦

⎤

⎢

⎣

⎡

ζ

+

+γ

=−

1

M

1

2

ln

c

1

M1

2

lncss

2

1

p

2

1

p12

(1.46)

Очевидно, что положительное изменение энтропии в области

М

1

>1 и отри-

цательное – в области

М

1

<1 для газов, когда 1< γ <1.67. Таким образом, уравне-

ние (1.46) имеет силу только тогда, когда

М

1

больше 1. Другими словами, разрыв-

ное течение реализуется только когда

М

1

> 1. Эта поверхность разрыва, перпенди-

кулярная направлению потока, является нормальной ударной волной. Число Маха

на выходе всегда меньше 1, и отношение давлений стагнации получается как

функция

М

1

с помощью уравнений (1.37) и (1.41). Отношения температур, давле-

ния и плотностей между ударной волной получаются как функции

М

1

с использо-

ванием уравнений (1.38-1.40) и уравнений (1.25-1.27). Характеристики нормаль-

ной ударной волны можно систематизировать следующим образом:

Фронт Ударная волна Позади

Скорость

u

1

> u

2

Давление p

1

< p

2

Плотность ρ

1

< ρ

2

Температура T

1

< T

2

Число Маха M

1

> M

2

Давление стагнации p

01

> p

02

Плотность стагнации ρ

01

> ρ

02

Температура стагнации T

01

= T

02

Энтропия S

1

< S

2

1.2.3 Сверхзвуковое течение в сопле

Когда газ движется из зоны стагнации через сопло при условии изоэнтро-

пийного изменения, изменение энтальпии характеризуется уравнением (1.23).

Скорость потока получается при подстановке уравнения (1.14) в уравнение (1.24):

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−=

Cp

Rg

p

Tcu

0

2

12 (1.47)

Подстановка уравнений (1.6) и (1.47) дает следующую зависимость:

2

1

0

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

=

−

γ

p

TRu

g

(1.48a)

Скорость истечения на выходе из сопла составляет:

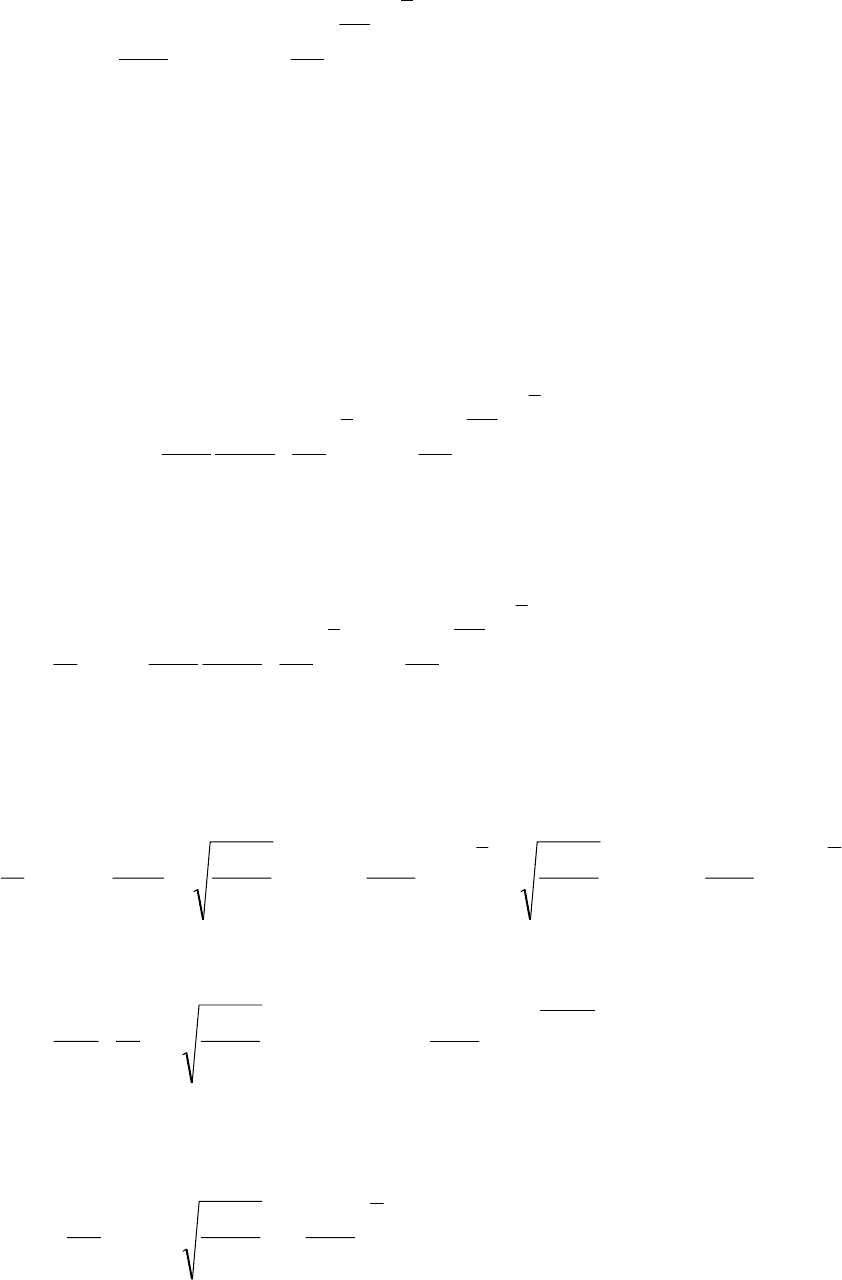
15

2

1

0

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

=

−

γ

p

TRu

e

ge

, (1.48b)

где подстрочный индекс e означает выход из сопла. Массовая скорость потока за-

дается законом сохранения массы при стационарном одномерном течении:

m

&

= ρ uA , (1.49)

где

m

&

– массовая скорость потока в сопле, ρ – плотность газа, А – площадь по-

перечного сечения сопла.

Подставляя уравнения (1.48), (1.5), (1.14) в уравнение (1.49), получаем:

2

1

0

2

00

0

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=

−

γ

p

TR

Apm

g

&

(1.50)

Таким образом, массовый поток определяется как m

&

/А.

2

1

0

2

00

0

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=

−

γ

p

TR

p

A

m

g

&

(1.51а)

Массовый поток также выражается как функция числа Маха, используя

уравнение (1.25) и (1.26):

2

0

2

1

2

0

2

1

2

1

ζ

γγγγ

ρ

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+=

⎟

⎠

⎞

⎜

⎝

⎛

−

+=== MMp

TR

MpM

TRTR

pu

u

A

m

ggg

&

(1.51b)

Дифференцирование уравнения (1.51b) дает выражение

()

12

31

22

0

2

1

11

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+−=

⎟

⎠

⎞

⎜

⎝

⎛

γ

γγ

MMp

TRA

m

dM

d

g

&

(1.51с)

Очевидно, что m

&

достигает максимума при М = 1. Максимальный массовый

поток ( m

&

/А)

max

получается, когда поперечное сечение равно А

*

:

2

0

max

1

2

ζ

γ

⎟

⎠

⎞

⎜

⎝

⎛

+

=

⎟

⎠

⎞

⎜

⎝

⎛

∗

p

TR

A

m

g

&

(1.52)

Таким образом, отношение А/А

*

получают как

16

2

1

21

ζ

γ

⎭

⎬

⎫

⎩

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

∗

M

A

(1.53)

Число Маха потока в сечении А получается с использованием уравнения

(1.53), когда задаются m, T

0,

p

0

, R

g

и γ.

Дополнительно получают Т, р и ρ при использовании уравнений (1.25),

(1.26) и (1.27). Дифференцирование уравнения (1.53) относительно числа Маха

описано уравнением (1.54)

21

2

1

2

1

21

ζ

γ

γγ

−

∗

⎭

⎬

⎫

⎩

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

+

++

−

=

⎟

⎠

⎞

⎜

⎝

⎛

M

A

dM

d

(1.54)

Уравнение (1.54) показывает, что А/А* достигает минимума при М = 1. Чис-

ло Маха потока увеличивается по мере уменьшения А/А*, когда М<1, и также

увеличивается, когда А/А* увеличивается и число Маха больше 1. Когда М = 1,

получается

зависимость А = А*, и она не зависит от γ. Очевидно, что А* является

минимальным поперечным сечением сопла, так называемым критическим сечени-

ем, где скорость потока становится равной скорости звука. Кроме того, скорость

увеличивается в дозвуковом потоке в сужающейся части и также увеличивается в

сверхзвуковом потоке расширяющейся части.

Скорость u

*

, температура Т

*

, давление р

*

и плотность ρ

*

в критическом се-

чении сопла получаются с использованием уравнений (1.16), (1.18), (1.19), (1.20):

TRu

g

γ=

∗

, (1.55)

1

2

0

+

=

∗

γ

T

, (1.56)

1

0

1

2

−

∗

⎟

⎠

⎞

⎜

⎝

⎛

+

=

γ

p

, (1.57)

1

0

1

2

−

∗

⎟

⎠

⎞

⎜

⎝

⎛

+

=

γ

ρ

(1.58)

Например, Т

*

/T

0

= 0,833, p

*

/p

0

= 0,528 и ρ

*

/ρ

0

= 0,664 получают, когда γ = 1,4.

Температура Т

0

в условиях стагнации уменьшается на 17%, а давление р

0

умень-

шается на 50% в критическом сечении (горловине) сопла. Давление уменьшается

быстрее, чем уменьшается температура, когда поток расширяется в сужающемся

сопле.

Максимальная скорость потока получается на входе в расширяющуюся

часть сопла. Когда на выходе из сопла создается вакуум, достигается максималь-

ная скорость (использование уравнения (1.48) и (1.6)):

17

0max

1

2

T

M

R

u

g

e

−

=

γ

(1.59)

Эта максимальная скорость зависит от молекулярной массы М

g,

, удельной

теплоемкости

γ и температуры стагнации Т

0

. Скорость увеличивается по мере то-

го, как

γ и М

g

уменьшаются и Т

0

увеличивается. Основываясь на уравнении (1.52),

упрощенное выражение для массовой скорости потока через критическое сечение

сопла А

t

(= А

*

) и давление в камере р

с

(= р

0

) может быть записано в следующем ви-

де:

ctD

pAcm =

&

, (1.60)

где с

D

– коэффициент разгрузки сопла (расширения)

ζ

γ

⎟

⎠

⎞

⎜

⎝

⎛

+

=

1

2

0

RT

M

c

g

D

(1.61)

1.3 Образование реактивных сил

1.3.1 Изменение количества движения и тяга

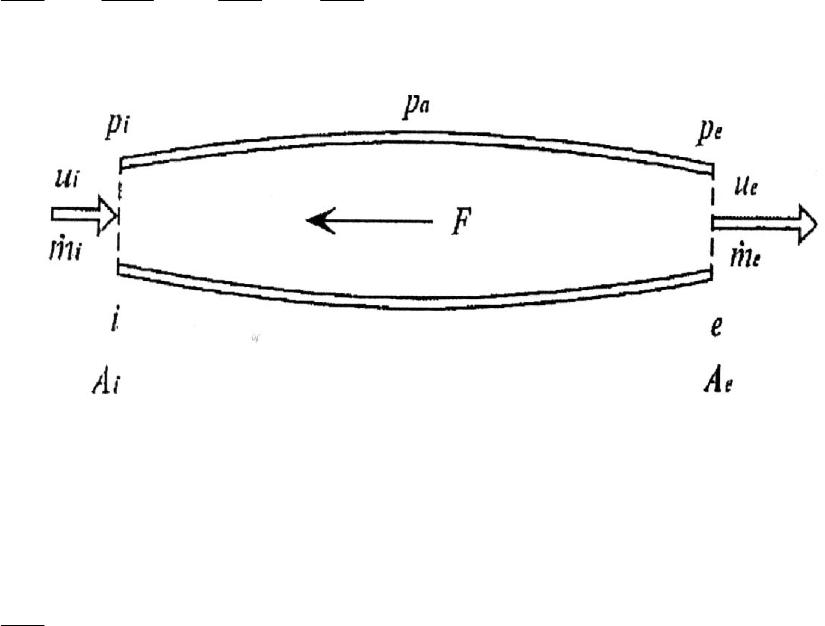
Предположим, что ракетная система, движущаяся в атмосфере, может быть

представлена так, как показано на рис. 1.3. Воздух поступает с переднего торца i ,

проходит через камеру сгорания с и выходит через выходное отверстие е. Тепло,

выделяющееся при сгорании высокоэнергетического материала, передается в ка-

меру сгорания. Баланс количества движения для создания тяги F может быть

за-

писан в следующем виде:

()( )

(

)

iiiieeeeiea

ApumApumAApF

+

−

+=−+

&&

, (1.62)

m

&

i

u

i

– количество движения, поступающее через сечение i;

m

&

i

u

е

– количество движения, выходящее через сечение е;

р

i

A

i

– сила, создаваемая давлением в сечении i;

р

е

А

е

– сила, создаваемая давлением, действующим в сечении е;

F + p

a

(A

e

–A

i

) – сила, действующая на внешнюю поверхность двигателя,

где u – скорость истечения,

m

&

– массовый поток, А – площадь поперечного се-

чения, индекс i относится к входу, а е – к выходу потока, а – атмосферное давле-

ние. Массовый поток высокоэнергетического материала m

p

, создаваемого в каме-

ре сгорания, задается разницей выходящего потока массы и входящего потока

массы m

&

е

– m

&

i

. В случае реактивного движения передний конец камеры закрыва-

ется (А

i

= 0) и поток, входящий в камеру сгорания, отсутствует (

m

&

I

= 0). Таким

образом, тяга, создаваемая в этом случае, равна

F =

е

m

&

u

e

+ A

e

(p

e

– p

a

), (1.63)

где m

&

p = m

&

g. Таким образом, тяга определяется скоростью потока и давлением

на выходе, когда задаются m

&

е

, А

е

и р

а

. Дифференцирование уравнения (1.63) отно-

сительно А

е

дает

18

ae

e

g

e

g

e

pp

dA

dp

A

dA

du

m

dA

dm

u

dA

dF

−+++=

&

(1.64)

Рис. 1.3. Изменение количества движения при реактивном движении

Уравнение количества движения на выходе из сопла записывается в виде

m

&

g

du

e

= –A

e

dp

e

и

g

md

&

= 0 при стационарном истечении из сопла. Из уравнения

(1.64) можно получить зависимость

ae

e

pp

dA

dF

−= (1.65)

Максимальная тяга получается при р

е

= р

а

, то есть в случае, когда давление

на выходе из сопла равно окружающему давлению.

Однако следует отметить, что уравнение (1.62) применимо к процессам ис-

течения в прямоточном воздушно-реактивном двигателе, а также в прямоточном

ракетном двигателе и в прямоточном воздушно-реактивном двигателе на твердом

топливе, потому что в этих случаях воздух поступает

через воздухозаборник и ус-

танавливается разность давлений между входом и выходом. Массовая скорость

потока из воздухозаборника

i

m

&

играет значительную роль в генерации тяги в слу-

чае прямоточного движения.

1.3.2 Ракетный двигатель

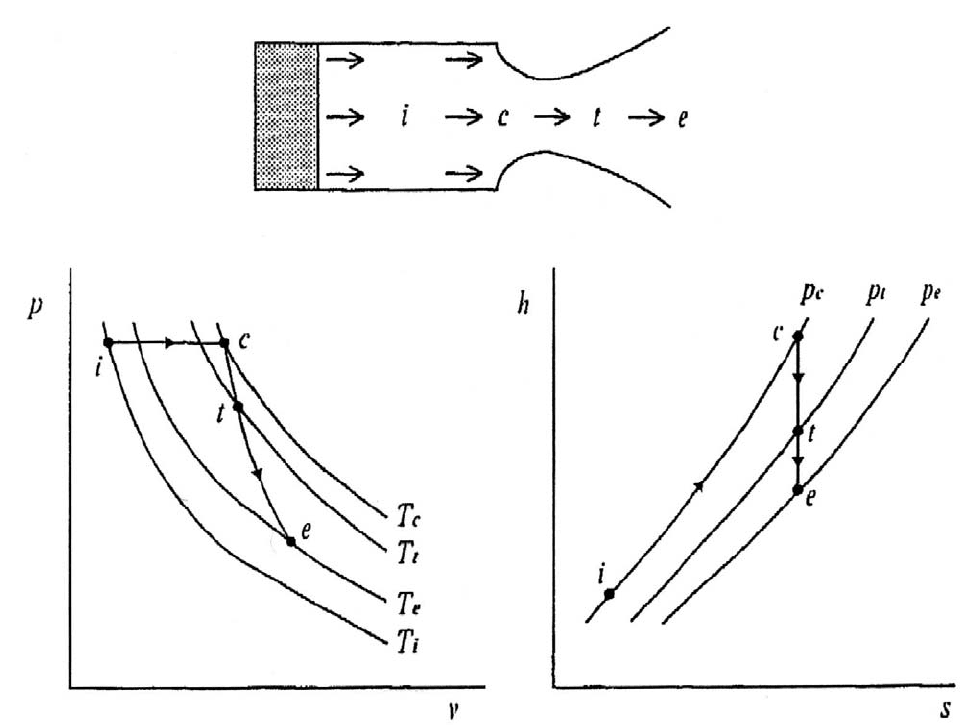
На рис. 1.4 представлена схема ракетного двигателя, состоящего из топлива,

камеры сгорания и сопла. Сопло обычно выполняется сходящимся-расходя-

щимся, чтобы ускорить движение продуктов сгорания от дозвукового до сверх-

звукового через горловину (критическое сечение) сопла. Термодинамически про-

цесс в ракетном двигателе показан также на рис. 1.4 в виде диаграмм давление-

объем и энтальпия

-энтропия [6].

19

Рис. 1.4. Диаграммы давление-объем и энтальпия-энтропия

Топливо, находящееся в камере сгорания, горит, генерирует продукты сго-

рания и увеличивает температуру от Т

i

до Т

с

при постоянном давлении р

с

.

Продукты сгорания расширяются через сужающееся сопло и создается давление

р

t

, температура достигает значения Т

t

в горловине сопла. Продукты сгорания про-

должают расширяться через расширяющуюся часть сопла и давление р

е

и темпе-

ратура Т

е

достигается на выходе из сопла. Если можно предположить, что (1) те-

чение одномерное и стационарное, (2) течение изоэнтропийное и (3) продукты

сгорания являются идеальным газом и отношение теплоемкостей является посто-

янным, то диаграммы зависимости р от v и h от s являются однозначно опреде-

ленными [6-9]. Изменение энтальпии, обусловленное горением топлива, составля-

ет

Δh = c

p

(Т

с

–Т

i

), (1.66)

где Δh – теплота реакции при сгорании топлива на единицу массы. Процесс

расширения с → t → е, приведенный на рис. 1.4, соответствует термодинамиче-

скому процессу, описанному в разделе 1.2.3 этой главы.

1.3.2.1 Коэффициент тяги

Тяга, создаваемая ракетным двигателем, описывается уравнением (1.63).

Подставляя уравнение (1.48b) и (1.52) в уравнение (1.63), получаем:

20

()

eac

c

e

ct

App

p

pAF −+

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

+−

=

−

+

2

1

2

1

2

1

2

γ

γγ

γ

(1.67)

Как видно из уравнения (1.65), максимальная тяга F

max

достигается при

р

е

= р

а

при данном отношении теплоемкостей газообразных продуктов сгорания:

2

1

2

max

1

2

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

+−

=

−

+

γ

γγ

γ

c

e

ct

p

pAF (1.68)

Уравнение (1.68) представляет собой упрощенное выражение тяги через

критическое сечение (горловину) сопла и давления в камере.

F = c

F

A

t

p

c

, (1.69)

где с

F

– коэффициент тяги, который определяют как

t

e

c

ae

c

e

F

A

p

pp

p

c

−

+

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

+−

=

−

+

2

1

2

1

2

1

2

γ

γγ

γ

(1.70)

Максимальный коэффициент тяги с

F

,

max

определяют как

2

1

2

max,

1

2

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

+−

=

−

+

γ

γγ

γ

c

e

F

p

c (1.71)

Если коэффициент расширения сопла стремится к бесконечности, то отно-

шение давлений р

с

/р

а

также стремится к бесконечности. Тогда максимальный ко-

эффициент тяги будет равен:

2

1

2

max,

1

2

1

2

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

+−

=

−

+

γ

γγ

γ

F

c (1.72)

Например, с

F, max

равен 2,246 для γ=1,20 и 1,812 для γ=1,40.

1.3.2.2 Характеристическая скорость

Характеристическая скорость с

*

определяется как

g

ct

m

pA

c

&

=

∗

(1.73)

Кубота Н. Твердые ракетные топлива и взрывчатые вещества

Подождите немного. Документ загружается.