Коврижных А.Ю., Конончук Е.А. и др. Прикладное программное обеспечение для решения экономических задач

Подождите немного. Документ загружается.

121

Известен план выпуска изделий: 60, 50, 35, 40 единиц соответственно.

Требуется найти затраты каждого вида сырья при заданном плане выпуска

изделий.

Решение

. Составим матрицу A и вектор q :

⎟

⎠

⎞

⎜

⎝

⎛

8654

2327

6521

5432

q =(60,50,35,40).

Для отыскания затрат каждого вида сырья требуется перемножить матрицы

и A. Получится матрица-строка b=

q A, где b[i]─затраты i-го вида сырья.

⎟

⎠

⎞

⎜

⎝

⎛

8654

2327

6521

5432

)40,35,50,60(b

=(120+50+245+160, 180+100+70+200, 240+250+105+240, 300+300+70+320)=

=(575, 550, 835, 990)

Посмотрим, как находятся затраты каждого вида сырья с помощью Maple.

Подключим пакет linalg.

with(linalg):

Создадим матрицу A

A:=matrix(4,4,[[2,3,4,5],[1,2,5,6],[7,2,3,2],[4,5,6,8]]);

:= A

⎡

⎣

⎢

⎤

⎦

⎥

2345

1256

7232

4568

Создадим матрицу-строку, соответствующую вектору

q:=matrix(1,4,[ 60,50,35,40]);

:= q []60 50 35 40

Функция multiply(U,V) умножает матрицу U на матрицу V.

Найдем матрицу b=

b:= multiply(q,A);

122

:= b []575 550 835 990

Задача 3.

Пусть затраты 4-х видов сырья на выпуск 4-х видов продукции определяются

таблицей 3. План выпуска продукции такой же, как в задаче 2. Требуется

найти

•

затраты на сырье, необходимое для производства одного изделия для

каждого вида продукции, и на перевозку этого сырья

•

общие затраты на сырье и его транспортировку

если известны себестоимости каждого вида сырья и его доставки

(соответственно 4, 6, 5, 8 и 2, 1, 3, 2 ден.ед.).

Решение. Составим матрицу себестоимостей сырья и его доставки

⎟

⎠

⎞

⎜

⎝

⎛

2312

8564

C .

Тогда, чтобы ответить на первый вопрос, нужно умножить матрицу A на

транспонированную матрицу

C :

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

47140

2971

3189

2986

8654

2327

6521

5432

Суммарные затраты на сырье и его доставку при векторе-плане выпуска

продукции

q определяются произведением вектора q на матрицу

AC :

)6185,17695(

47140

2971

3189

2986

)40,35,50,60(

⎟

⎠

⎞

⎜

⎝

⎛

ACq .

С помощью Maple получим:

with(linalg):

A:=matrix(4,4,[[2,3,4,5],[1,2,5,6],[7,2,3,2],[4,5,6,8]]);

:= A

⎡

⎣

⎢

⎤

⎦

⎥

2345

1256

7232

4568

123

> C:=matrix(2,4,[[4,6,5,8],[2,1,3,2]]);

:= C

⎡

⎣

⎢

⎤

⎦

⎥

4658

2132

q:=matrix(1,4,[ 60,50,35,40]);

:= q []60 50 35 40

Функция transpose(M) возвращает транспонированную матрицу. Произведе-

ние матриц A и

C обозначим через G.

G:= multiply(A, transpose(C));

:= G

⎡

⎣

⎢

⎤

⎦

⎥

86 29

89 31

71 29

140 47

Таким образом, найдены затраты на сырье, необходимое для производства

одного изделия для каждого вида продукции, и на перевозку этого сырья.

Пусть n─вектор, указывающий общие затраты на сырье и его

транспортировку, т. е.

ACqn = .

n:= multiply(q,G);

:= n []17695 6185

2. Использование систем линейных уравнений.

Задача 4. Прогноз выпуска продукции по запасам сырья.

Предприятие выпускает три вида продукции, используя сырье трех типов.

Необходимые характеристики производства указаны в таблице 3.

Расход сырья по видам продукции,

вес.ед./изд.

Вид

сырья

1 2 3

Запас сырья,

вес.ед.

1 6 4 5 2400

2 4 3 1 1450

3 5 2 3 1550

Таб. 3.

124

Требуется определить объем выпуска продукции каждого вида при

заданных запасах сырья.

Решение

. Обозначим неизвестные объемы выпуска продукции через

321

,, xxx . Тогда при условии полного расхода запасов для каждого вида сырья

можно записать балансовые соотношения, которые образуют систему трех

уравнений с тремя неизвестными:

⎪

⎩

⎪

⎨

⎧

=++

1550325

145034

2400546

321

xxx

Решая эту систему уравнений любым способом (например, по правилу

Крамера или методом Гаусса), находим, что при заданных запасах сырья

объемы выпуска продукции составят по каждому виду соответственно

100,250,150

321

=== xxx .

Для использования системы Maple для решения системы вспомним, что

нужно составить матрицу из коэффициентов системы

⎟

⎠

⎞

⎜

⎝

⎛

325

134

546

, вектор-столбец свободных членов системы

⎟

⎠

⎞

⎜

⎝

⎛

1550

1450

2400

Тогда вектор-решение

⎟

⎠

⎞

⎜

⎝

⎛

определится по формуле bAx

1−

= , где

1−

A ─

матрица, обратная к матрице A, для отыскания которой в системе Maple

имеется функция inverse(A).

with(linalg):

A:=matrix(3,3,[[6,4,5],[4,3,1],[5,2,3]]);

:= A

⎡

⎣

⎢

⎤

⎦

⎥

645

431

523

b:= vector(3,[2400,1450,1550]);

:= b [],,2400 1450 1550

x:= multiply(inverse(A),b);

[],,150 250 100

125

4. Графики функций и их приложения

Задача 5. Кривые спроса и предложения. Точка равновесия.

Рассмотрим зависимость спроса D и предложения S от цены P. Чем меньше

цена, тем больше спрос при постоянной покупательной способности

населения. Обычно зависимость D от P имеет вид ниспадающей кривой,

которую можно задать формулой

cPD

+= , где c, a ─ константы, a<0.

Предложение растет с увеличением цены на товар, и потому зависимость S

от P имеет форму

dPS

+= , где d, b ─ константы, b≥1.

Для экономики представляет интерес условие равновесия, т. е. когда спрос

равен предложению. Это условие дается уравнением D(P)=S(P) и

соответствует точке пересечения кривых D и S. Значение P

, при котором

кривые пересекаются, называется равновесной ценой. Найдем приближенно

значение равновесной цены при a=-1/2, b=2, c=2 ,d=1, 0.1<P<3.

Рассмотрим графики этих кривых при a=-1/2, b=2, c=2 ,d=1, 0.1<P<3.

Решение

. Графики D(P) и S(P) нетрудно получить с помощью программы

Maple. Они строятся так:

Зададим параметры a, b, c, d:

a:=-0.5: b:=2: c:=2: d:=1:

Определим функции D(P) и S(P):

D(P):=P^a + c: S(P):= P^b + d:

Для построения графиков используется функция plot

plot([D(P), S(P)], P=0.1..3, color=black);

Получим графики D(P) и S(P):

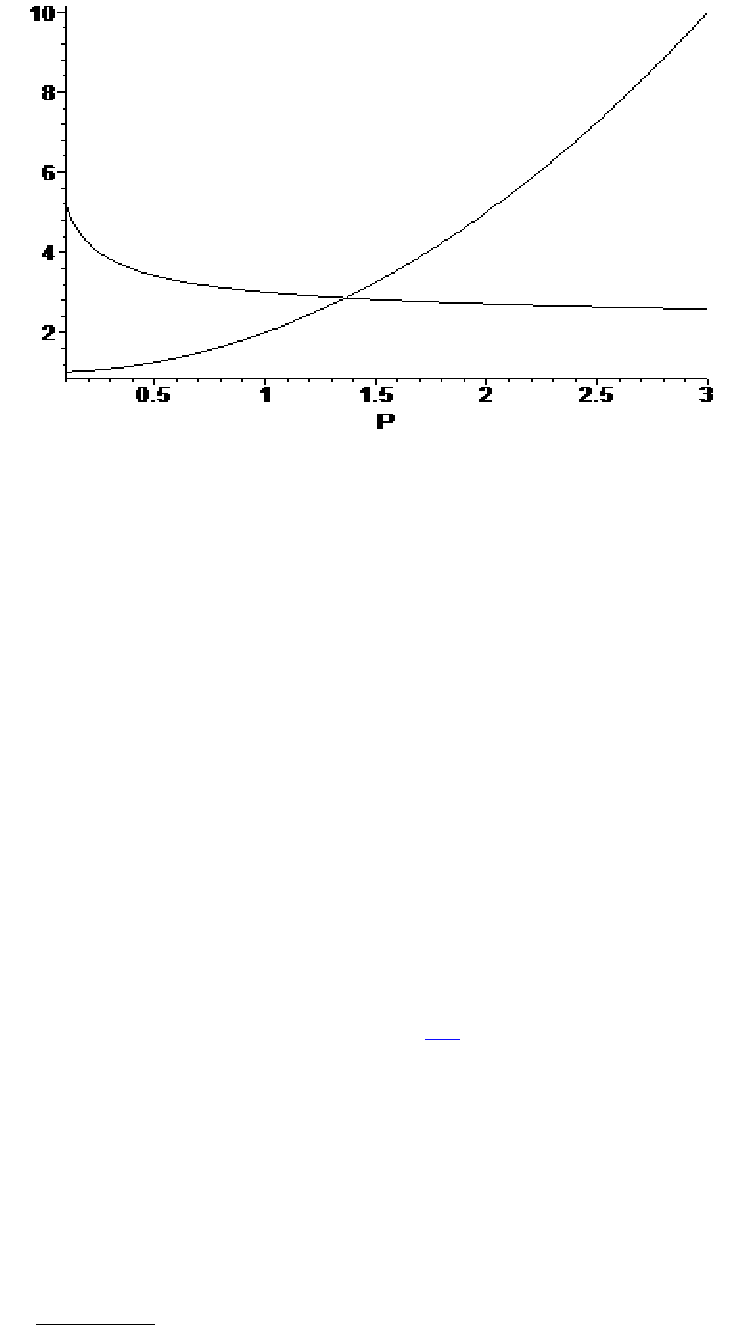
126

По графику нетрудно определить приближенное значение P

. Равновесная

цена приближенно равна 1,35.

Заметим, что с помощью программы Maple легко провести исследование

поведения кривых спроса D и предложения S при разных значениях

параметров a, b, c, d и посмотреть, как при этом меняется значение

равновесной цены P

Для того, чтобы найти значение равновесной цены P

более точно, нужно

решить уравнение D(P)=S(P). В системе Maple для отыскания действительных

решений уравнения используется функция fsolve

a:=-0.5: b:=2: c:=2: d:=1:

D(P):=P^a + c: S(P):= P^b + d:

eq:=D(P)=S(P);

:= eq = +

2 + P

fsolve(eq,P);

1.362598578

4. Использование понятия производной

Задача 6. Объем продукции u (усл.ед.) цеха в течение рабочего дня

представляет функцию

425755

++−−= tttu

, где t ─ время (ч). Найти

производительность труда через 2 часа после начала работы.

127

Решение.

Пусть функция u=u(t) выражает количество произведенной продукции u за

время t. Необходимо найти производительность труда в момент t

За период времени от t

до t

+∆t количество произведенной продукции

изменится от значения u(t

) до значения u(t

+∆t). Тогда средняя

производительность труда за этот период времени равна

tuttu

∆

−

∆+ )()(

Производительность труда в момент t

можно определить как предельное

значение средней производительности

tuttu

∆

−

∆

→∆

)()(

lim

, а это производная

)(

Таким образом, чтобы найти производительность труда через 2 часа после

начала работы, вычислим производную

(

)

=++−−=

23'

425755 tttu

75103

+−− tt и найдем ее значение при t=2. Получим, что

производительность труда через 2 часа после начала работы равна 43 усл.ед./ч.

В системе Maple производные вычисляются очень легко. Для отыскания

производной используется функция diff. Функция diff (f(x),x) вычисляет

производную от f(x) по переменной x . Функция Diff используется для

математической записи значка производной: Diff (f(x),x) выводит на экран

)(xf

x∂

∂

Diff (-t**3-5*t**2+75*t+425,t)= diff (-t**3-5*t**2+75*t+425,t);

∂

()− − + + t

5 t

75 t 425 − − + 3 t

10 t 75

Для вычисления значения производной при конкретном значении t присвоим

переменной y1 выражение, равное производной.

y1:=diff (-t**3-5*t**2+75*t+425,t);

:= y1

−

+ 3 t

10 t 75

Вычислим ее значение при t, равном 2.

subs(t=2,y1);

128

Задача 7. Зависимость между себестоимостью единицы продукции y (тыс.

руб.) и выпуском продукции x (млн. руб.) выражается функцией y=-0,5x +80.

Найти эластичность себестоимости при выпуске продукции, равном 60 млн.

руб.

Решение

. Эластичностью функции )( yE

называется предел отношения

относительного приращения функции y к относительному приращению

переменной x при

0→

∆

x :

.limlim)(

⋅=

∆

⎟

⎠

⎞

⎜

⎝

⎛

∆∆

→∆→∆

Эластичность функции показывает приближенно, на сколько процентов

изменится функция y=f(x) при изменении независимой переменной x на 1%.

В задаче 7 эластичность себестоимости определяется так:

160

)5,0(

805,0

)(

−

=−

+−

При x=60 эластичность равна -0,6, т.е. при выпуске продукции, равном 60

млн. руб., увеличение его на 1% приведет к снижению себестоимости на 0,6%.

С помощью системы Maple получим

y(x):=-0.5*x+80;

:= ()y

−

+ .5

y1:= diff(y(x),x);

:= y1 -.5

E:=x/y(x)*y1;

:= E −.5

− + .5 x 80

Чтобы упростить полученное выражение используется функция simplify

simplify(%);

− x 160.

Чтобы найти эластичность себестоимости при выпуске продукции, равном 60

млн. руб., определим переменную E1, равную полученному выражению.

E1:= %;

129

:= E1

− x 160.

subs(x=60.,E1);

-.6000000000

5. Задачи на экстремум.

Задача 8. Капитал в 1 млрд. рублей может быть размещен в банке под 50%

годовых или инвестирован в производство, причем эффективность вложения

ожидается в размере 100%, а издержки задаются квадратичной зависимостью.

Прибыль облагается налогом в p%. При каких значениях p вложение в

производство является более эффективным, чем чистое размещение капитала в

банке?

Решение.

Пусть x (млрд. рублей) инвестируется в производство, а 1-x −

размещается под проценты. Тогда размещенный капитал через год станет

равным

()

⎟

⎠

⎞

⎜

⎝

⎛

+−

100

11 x

= x

−

, а капитал, вложенный в производство:

⎟

⎠

⎞

⎜

⎝

⎛

100

=2x. Издержки составят

)1(

αα

x , т.е. прибыль от вложения в производство

2 xxC

−=

. Налоги составят

()

100

−

, т.е. чистая прибыль окажется равной

()

100

1 xx

−

⎟

⎠

⎞

⎜

⎝

⎛

−

Общая сумма через год составит

()

=−

⎟

⎠

⎞

⎜

⎝

⎛

−+−=

100

)( xx

xxA

100

⎟

⎠

⎞

⎜

⎝

⎛

−−

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

−+

. Требуется найти максимальное значение этой

функции на отрезке [0;1].

Найдем

⎟

⎠

⎞

⎜

⎝

⎛

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−=

100

12)(

130

Она равна нулю при

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

100

. 0

100

12)(

⎟

⎠

⎞

⎜

⎝

⎛

−−=

, т.е. согласно

второму достаточному условию экстремума

x − точка максимума.

Чтобы

x принадлежало отрезку [0;1], необходимо выполнение условия

⎟

⎠

⎞

⎜

⎝

⎛

−<−

⎟

⎠

⎞

⎜

⎝

⎛

−<

100

120

. Отсюда

Таким образом, если

25≥p , то выгоднее ничего не вкладывать в

производство и разместить весь капитал в банк. Если

p , то можно

показать, что при

)0(

100

)(

xA =>

⎟

⎠

⎞

⎜

⎝

⎛

−

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

−

т.е. вложение в производство является более выгодным, чем чистое

размещение в банке под проценты.

С помощью системы Maple получим следующее.

Для отыскания точек локального экстремума воспользуемся тем, что в точке

экстремума производная обращается в 0. Выполним следующие действия:

определим функцию

)(xA

(α=alp); переменной dA присвоим значение

производной от функции A(x); с помощью функции solve решим уравнение

0)(

=xA и найдем точку экстремума

x ; найдем максимальное значение

функции

)(xA , равное )(

xA .

A:=(x)->(1-x)*3/2+(2*x-alp*x^2)*(1-p/100);

:= A → x − +

x () − 2 x alp x

⎛

⎝

⎜

⎞

⎠

⎟

− 1

100

dA:=diff(A(x),x);

:= dA − +

() − 22alp x

⎛

⎝

⎜

⎞

⎠

⎟

− 1

100

x0:=solve(dA,x);