Конспект лекцій - Економетричне моделювання

Подождите немного. Документ загружается.

МЕТОД ВІДХИЛЕНЬ

6.1. Попередні перетворення вихідних даних

Раніше, при розбитті даних на однорідні сукупності, потрібно

було провести перетворення даних. У процедурі, що пропонується ни-

жче, потрібно ввести додатковий розподіл ознак на стимулятори, де-

стимулятори та номінатори. У загальному випадку вони визначаються

таким чином.

Ознака X називається стимулятором, якщо

(

)

(

)

jiji

nnxx f⇒≥ . (6.1)

Тобто, якщо значення ознаки для одного об’єкта більше за

значення цієї ознаки для іншого об’єкта виплаває домінування першо-

го об’єкта над іншим:

(

)

(

)

jiji

nnxx p⇒≥ , (6.2)

для номінатора:

(

)

()

jijik

jikji

nnxxx

⇒≥≥

, (6.3)

або:

(

)

()

jijik

jikji

nnxxx

⇒≥≥

(6.4)

Тобто, спочатку ознака веде себе, як стимулятор (дестимулятор),

а після досягнення деякого значення – як дестимулятор (стимулятор).

Вищезгадані типи ознак уведені для того, щоб врахувати їхній

“економічний” зміст. Наприклад, ознака, що виражає продуктивність

праці, є стимулятором, а ознака, яка виражає собівартість продукції –

дестимулятором. Розглянемо ознаку, що описує якість виробленого

виробу. При виробництві цигарок встановлений певний рівень вологості.

Поки цей рівень не досягнутий, ознака має характер стимулятора; оп-

тимальною точкою є граничний (плановий) рівень вологості. Далі

ознака поводиться як дестимулятор.

Для того щоб проводити подальший аналіз, потрібно перетво-

рити дестимулятори в стимулятори. Ця операція виробляється відповід-

но до однієї з формул:

−

, (6.5)

' =

. (6.6)

Номінатори заміняються ознаками, що мають близьку змістовну

інтерпретацію, але у той самий час є стимуляторами або дестимуляторами.

Перетворення дестимуляторів у стимулятори необхідно тому,

що у пропонованому далі методі використовується ізоморфічне пере-

творення ознак. Воно дає позитивні результати тільки тоді, коли дослі-

джувана сукупність ознак складається зі стимуляторів. У цьому випад-

ку спостерігається так звана позитивна кореляційна залежність: зрос-

тання значень однієї ознаки викликає зростання значень інших ознак.

6.1. Алгоритм методу відхилень

Ідея методу полягає в переході від багатомірних об’єктів до

двовимірних. Це дає можливість графічно зобразити результат і про-

вести попередній візуальний розподіл сукупності об’єктів на однорідні

підмножини.

Алгоритм методу укладається в послідовність таких кроків.

Крок 1. Перетворення дестимуляторів у стимулятори.

Крок 2. Визначення полюсів сукупності. Полюсом є точка, яка

має найбільші (верхній полюс) або всі найменші (нижній полюс) зна-

чення ознак. При цьому така точка може не входити в сукупність даних.

* * *

Позначимо верхній полюс через

P (x , x , …, x

B n1 2

), а нижній

через

P (x , x

H 1* 2*

, …, x ).

Крок 3.

Перенос системи координат у нижній полюс. При цьо-

му значення вихідних даних перетворюється за формулою:

u = x

ij ij

– x

(6.7)

Слід зауважити, що координати нижнього та верхнього полю-

сів також перетворюються відповідно до (6.7), однак для зручності

позначення їх координат ми залишимо без змін.

Крок 4. Здійснення побудови осі сукупності даних. Вісь має

таке рівняння:

= x ·t, (6.8)

де

t – параметр прямої.

Ця пряма являє собою найбільшу вісь сукупності в багатови-

мірному просторі. Відхилення від точок-спостережень від цієї осі да-

ють інформацію про їх розташування.

Крок 5. Знаходження прямокутних проекцій точок на вісь. Поз-

начимо їх через

R = (y y …, y

i i1

,). Координати проекції обчислю-

ються за формулою:

= x · t

j i

, (6.9)

∑

ijj

)(

де

. (6.10)

Крок 6.

Визначення відхилень точок-об’єктів від осі сукупнос-

ті. Будемо вважати, що лінійне упорядкування об’єктів

відповідає

упорядкуванню проекцій

цих об’єктів. Отже, воно збігається з чер-

говістю розташування точок

на осі сукупності, тобто з порядком, що

відповідає відстаням точок від нижнього полюса

. У ролі відхилень

виступають показники:

2/1*

2/1

]))([(

iiii

RPRPW

PRPRM

−−=

(6.10)

Компоненти цих показників обчислюються за формулами:

.)(

;

∑

−=

sjsjs

sjs

yuw

(6.11)

Перший показник задає відстань точок-проекцій від нижнього

полюса ( в новій системі – від початку координат), а другий – відстань

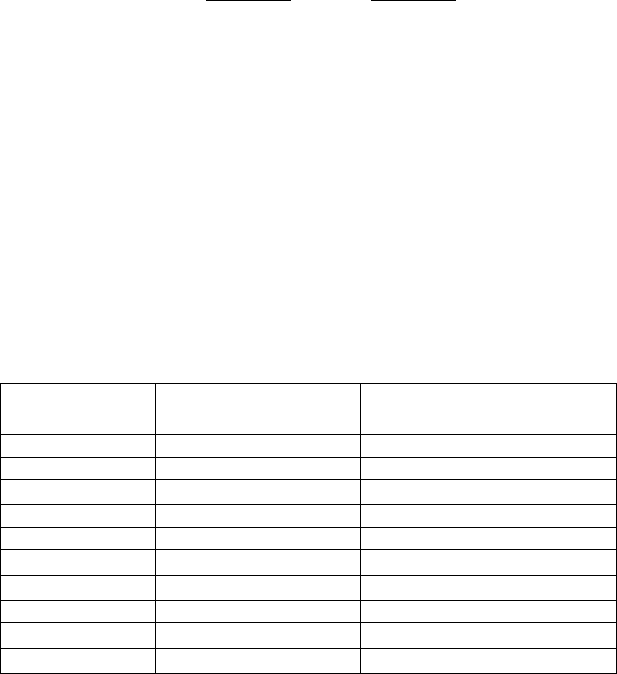
між точками-об’єктами та їх прямокутними проекціями на вісь сукуп-

ності. Величини

M* та W* рекомендується нормувати, щоб їх значен-

ня лежали в межах від 0 до 1.

}{

max

}{

max

m ==

(6.13)

Крок 7. Побудова в площині MOW діаграми розсіювання ознак.

За видом визначається слід розподілу ознак. Помітимо, що для бага-

томірних величин важко визначити знак ( + чи –) для відхилень точок

сукупності. Тому діаграма розсіювання зображається лише в першому

квадранті системи координат

MOW. Враховуючи цю особливість; фор-

ма сліду розподілу буде визначена наближено.

Приклад 6.1

Нехай відомі такі дані по 10 підприємствам: X

– продуктив-

ність праці,

– індекс зниження собівартості продукції. Потрібно

розбити сукупність даних на однорідні підмножини. Вихідні дані на-

ведені у таблиці 6.1.

Таблиця 6.1

Продуктивність Індекс зниження

Підприємство, n

праці,

собівартості продукції,

1 2

1 5,88 52,6

2 6,3 46,6

3 8,17 172,1

4 9,12 56,5

5 9,26 204,2

6 9,35 62

7 9,38 209,6

8 9,87 53,1

9 10,81 236,7

10 12,11 222,6

Розв’язування

Виконаємо розрахунки відповідно до алгоритму, наведеного в

описі методу. Вихідні дані є стимуляторами, тому крок 1 пропускаємо.

Результати виконання кроків 2, 3 та 4 занесемо до таблиці 6.2. Діагра-

ма розсіювання точок-об’єктів зображена на рис 6.1. На ній же зобра-

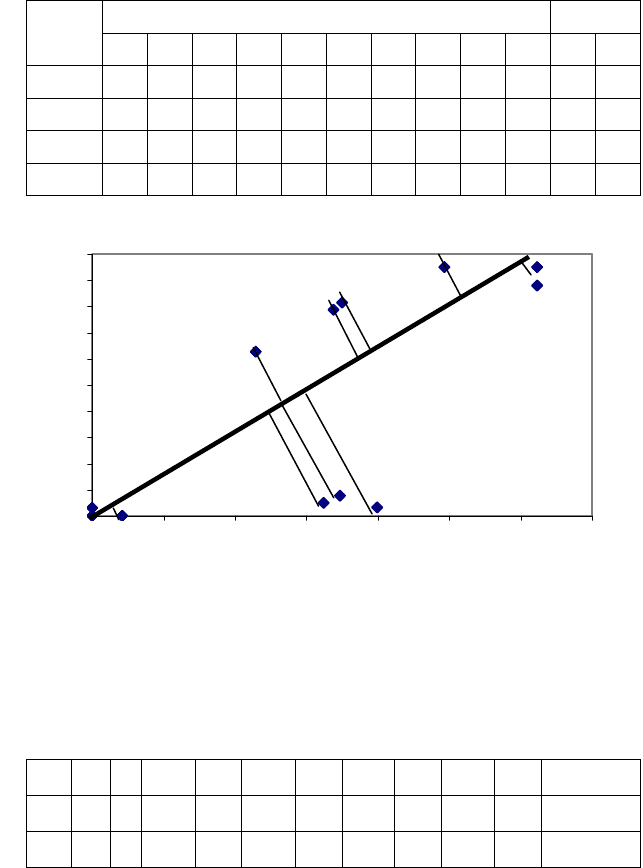
зимо вісь сукупності, яка проходить через точки верхнього та нижньо-

го полюсів.

Таблиця 6.2

Об’єкт Полюс

Ознака

1 2 3 4 5 6 7 8 9 10

Р Р

н в

X 5,88 6,3 8,17 9,12 9,26 9,35 9,38 9,87 10,8112,11 5,88 12,11

X 52,6 46,6 172,1 56,5

04,2 62

09,6 53,1

36,7

22,6 46,6

36,7

U 0 0,42 2,29 3,24 3,38 3,47 3,5 3,99 4,93 6,23 0 6,23

U 6 0 125,5 9,9 157,6 15,4 163 6,5 190,1 176 0 190,1

100

120

140

160

180

200

01234567

Рис. 6.1 – Діаграма розсіювання точок-об’єктів даних

Знайдемо координати проекцій на вісь сукупності (формула 6.9).

Для цього обчислимо величини

за формулою (6.10). Необхідні для

цього розрахунки занесемо до таблиць 6.3 та 6.4.

Таблиця 6.3

·U

0 2,62 14,27 20,19 21,06 21,62 21,81 24,86 30,71 38,81

(х

)

+ ( х

)

·U

1140,6 0 23857,551881,9929959,762927,54 30986,3 1235,6536138,0133457,6 36176,82

0,03 0,00 0,66 0,05 0,83 0,08 0,86 0,03 1,00 0,93

Обчислимо відхилення точок-спостережень від осі сукупності (фор-

мула 6.11). Результати обчислень занесемо до таблиці 6.4 разом з координа-

тами проекції на вісь сукупності координати проекцій точок-спостережень на

вісь сукупності. Значення показників

M та W пронормуємо.

Таблиця 6.4

2 2 2

M* M (U

s s 1

-Y (U

)

-Y W* W

)

s s

0,04 35,92 35,96 6 0,03 0,04 0 0,2 0,05

0 0 0 0,01 0 0,18 0 0,42 0,11

16,9 15735,27 15752,17 125,51 0,66 3,32 0 1,82 0,48

0,11 99,91 100,02 10 0,05 8,48 0,01 2,91 0,77

26,66 24819,35 24846 157,63 0,83 3,18 0 1,78 0,47

0,26 240,16 240,42 15,51 0,08 8,77 0,01 2,96 0,79

28,51 26549,35 26577,86 163,03 0,86 3,39 0 1,84 0,49

0,05 43,87 43,92 6,63 0,03 14,23 0,02 3,77 1

38,8 36121,83 36160,63 190,16 1 1,69 0 1,3 0,34

33,27 30981,33 31014,6 176,11 0,93 0,21 0 0,46 0,12

Max = 190,16 Max = 3,77

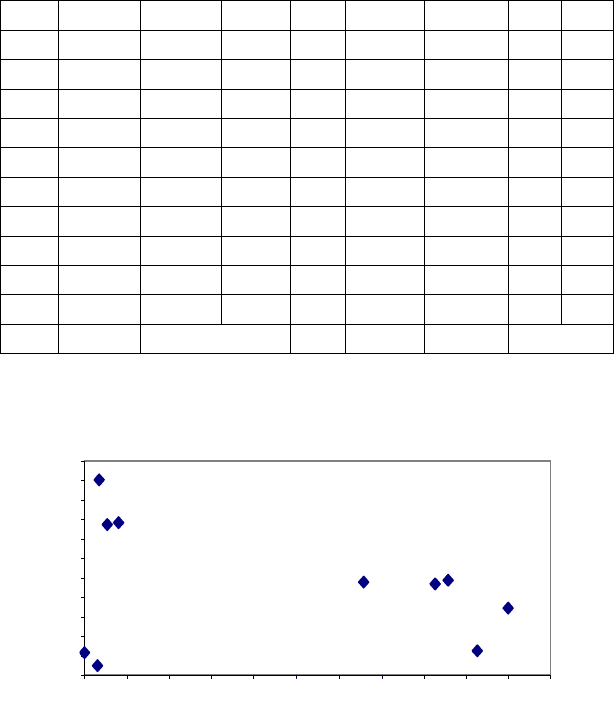
Зобразимо точки-об’єкти в системі координат

MOW (рис. 6.2).

У результаті за виглядом одержаного зображення можна зробити та-

кий висновок про однорідність даних.

0,00

0,10

0,20

0,30

0,40

0,50

0,60

0,70

0,80

0,90

1,00

1,10

0,00 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00 1,10

Рис. 6.2 – Зображення об’єктів в системі координат MOW

Вся сукупність розбивається на 4 ізоморфічно однорідних під-

множини:

= { n

, n

};

= { n

, n

};

= { n

, n

};

= { n

, n

6.3. Діаграма Чекановського

Ідея методу полягає в побудові на основі матриці відстаней

між об’єктами діаграми і перетворення її до виявлення скупчень

об’єктів. Кожне таке скупчення буде являти собою ізоморфічно одно-

рідну підмножину даних.

Алгоритм методу полягає в наступному.

Перших три кроки аналогічні методу відхилень. Всі подальші

обчислення проводяться на основі перетворених даних

, одержаних

за формулою (6.7).

Крок 4. Ізоморфічне перетворення величин u

за формулою 5.7:

Крок 5. Обчислення за значеннями величин z

матриці відста-

ней між точками

.Відстань між об’єктами знаходиться за формулою

евклідової метрики (формула 5.9)

Крок 6. Побудова за матрицею відстаней діаграми Чекановсь-

кого. Значення матриці відстаней розбиваються на класи з наперед

визначеними інтервалами можливих значень. Найпростішим , а тому і

найбільш часто застосовуваним є розбиття на два класи. Кожному зі

значень матриці відстаней ставиться у відповідність графічний сим-

вол: класу з меншими числовими значеннями відповідає один символ,

наприклад “

×”, а класу з великими значеннями – інший, наприклад,

символ “

”. Головною проблемою при цьому є вибір критичного зна-

чення відстані

d*, за яким здійснюється розподіл на великі та малі зна-

чення. У ролі такого значення можна обрати величину, обчислену за

правилами побудови радіуса для методу куль (див. т. 5). У результаті

буде отримана невпорядкована діаграма Чеканоського.

Крок 7. Упорядкування діаграми шляхом перестановки її ряд-

ків і стовпців. При цьому знаки “

×” по можливості необхідно зосере-

дити уздовж головної діагоналі. У результаті будуть одержані скуп-

чення цих знаків, які свідчать про однорідність відповідних об’єктів.

Крок 8. Визначення за діаграмою однорідних підмножин

об’єктів.

Якщо ж не вдається одержати упорядковану діаграму і симво-

ли “

×” залишаються розкиданими по всій таблиці, то виходить, що

попередньо виділені підмножини містять сильно розрізняються

об’єкти і ізоморфічно неоднорідні.

Приклад 6.2

Для даних (приклад 6.1) провести розбиття на ізоморфічно од-

норідні сукупності даних за допомогою діаграми Чекановського.

Розв’язування

Для даних таблиці 6.2 (змінні U

та U

) побудуємо матрицю

відстаней, яку занесемо до таблиці 6.5. Визначимо межу відстані для

поділу значень матриці на класи, рівну

d* = 7,26.

Таблиця 6.5

1 2 3 4 5 6 7 8 9 10

1 0,00 2,14 22,43 14,61 29,50 15,71 30,55 17,97 37,88 39,88

2 2,14 0,00 22,55 12,81 29,46 13,98 30,50 16,12 37,64 39,31

3 22,43 22,55 0,00 19,74 7,26 19,10 8,29 21,26 16,04 19,64

4 14,61 12,81 19,74 0,00 24,62 1,38 25,54 3,43 30,98 30,79

5 29,50 29,46 7,26 24,62 0,00 23,70 1,05 25,33 8,84 13,20

6 15,71 13,98 19,10 1,38 23,70 0,00 24,60 2,77 29,85 29,51

7 30,55 30,50 8,29 25,54 1,05 24,60 0,00 26,18 7,87 12,49

8 17,97 16,12 21,26 3,43 25,33 2,77 26,18 0,00 30,89 30,00

9 37,88 37,64 16,04 30,98 8,84 29,85 7,87 30,89 0,00 6,31

10 39,88 39,31 19,64 30,79 13,20 29,51 12,49 30,00 6,31 0,00

За даними матриці відстаней побудуємо діаграму Чекановсь-

кого (рис 6.3). Перший рядок та перший стовпчик діаграми містять

номери об’єктів.

1 2 3 4 5 6 7 8 9 10

1 X X

2 X X

3 X X

4 X X X

5 X X X

6 X X X

7 X X

8 X X X

9 X X

10 X X

Рис. 6.3 – Невпорядкована діаграма Чекановського

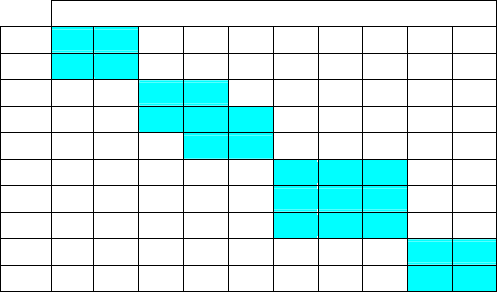
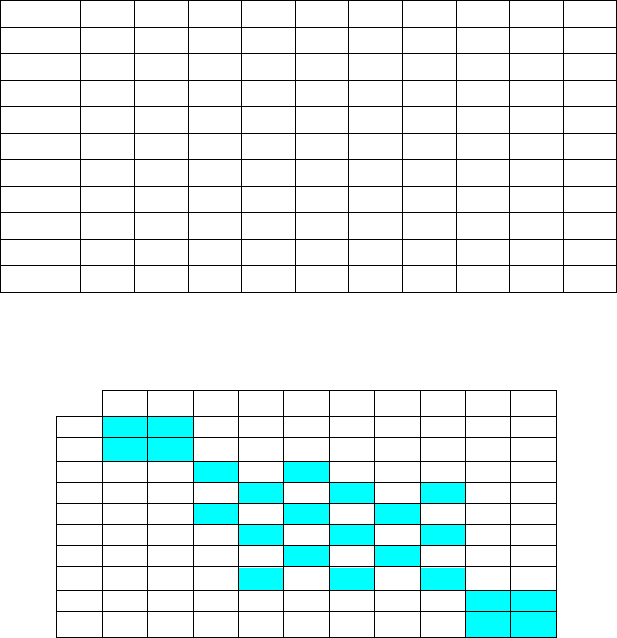
Впорядкуємо діаграму, переставивши рядки і стовпчики так,

щоб мало місце скупчення знаків “

Х” вздовж головної діагоналі діаг-

рами. Результат наведено на рис. 6.4.

1 2 3 5 7 4 6 8 9 10

X X

X X X

X X

X X X

X X

Рис. 6.4 – Впорядкована діаграма Чекановського

Як видно з діаграми, сукупність розбилась на чотири однорідні

підмножини:

= { n

, n

};

= { n

, n

};

= { n

, n

};

= { n

, n

Цей результат збігається з тим, який був одержаний за мето-

дом відхилень.

Питання для самоперевірки

1. Що собою являють стимулятори, дестимулятори та номіна-

тори?

У чому полягає сутність методу відхилень?

Охарактеризуйте основні кроки методу відхилень.

У чому полягає сутність побудови діаграми Чекановського?

Для чого потрібне впорядкування діаграми Чекановського?

ЗМЕНШЕННЯ КІЛЬКОСТІ

ВИХІДНИХ ОЗНАК

7.1. Види і властивості діагностичних ознак

У попередніх розділах як об’єкт аналізу розглядались реалізації

ознак. Тепер об’єктом аналізу будуть самі ознаки. Сукупності властивос-

тей

Ф, реалізації яких об’єднуються в матриці X = (x

) розмірності m × n,

називаються сукупностями вихідних ознак. Ознаки досить часто зв’язані

між собою і тому несуть ту саму або подібну інформацію про досліджу-

вані явища і процеси. Буває корисно скоротити число розглянутих

ознак, але так, щоб, з одного боку, кількість діагностичних ознак була

невеликою, а з іншого боку – не відбулося значної втрати інформації.

Виконання обох вимог можливо, коли діагностичні ознаки взаємонеза-

лежні, а ознаки, що не входять у число діагностичних, від них залежать.

Іноді висуваються додаткові вимоги, щоб діагностичні ознаки володіли

високою поділяючою здатністю і не залежали від зовнішніх впливів.

При цьому під діагностичними ознаками будемо розуміти ознаки, які

найбільш повно описують досліджуване явище чи процес і в результаті

аналізу залишились для побудови економетричної моделі.

Однак дві перших умови є найважливішими, тому методам

одержання діагностичних ознак із заданими властивостями приділя-

ється багато уваги. Усі методи поділяються на дві основні групи. До

першої групи відносяться ті, що дають неповну редукцію ознак. Їхнє

використання дозволяє значно скоротити кількість ознак, однак у су-

купності завжди залишається більш однієї ознаки. У другу групу вхо-

дять методи повної редукції ознак. З їхньою допомогою кількість

ознак зменшується до однієї.

Отже, нехай для дослідження відібрано

n ознак X

, X

, …, X

Неповну редукцію можна робити двома способами. Перший спосіб при-

водить до одержання так званих індивідуальних діагностичних ознак,

якими є деякі з вихідних ознак. Сукупність

Ф скорочується до сукупності:

{

}

XXXΦ ,...,,

′

, (7.1)

причому

p < n.

Другий спосіб полягає в побудові якихось синтетичних вели-

чин. Тоді сукупність

Ф зменшується, а її елементи перетворюються, і в

результаті одержуємо сукупність: