Конспект лекцій - Економетричне моделювання

Подождите немного. Документ загружается.

Залежність між характеристиками

X та Y моделюється як пра-

вило у вигляді функції

Y = f(X). “Стандартне” трактування цієї рівності

означає, кожному можливому значенню

X відповідає єдине визначене

значення

Y. На практиці встановлення залежності ускладнюється на-

явністю таких чинників:

− великою кількістю пояснюючих змінних;

− помилками спостереження змінних;

− неповною інформацією про вигляд залежності;

– обмеженістю кількості спостережень.

Тому результати оцінки залежностей носять наближений характер.

Розрізняють такі види статистичних залежностей.

1. Точні. Такі залежності будуються як інтерполяційні функції.

Завдання інтерполяції полягає у побудові за заданим набором значень

(x , y ), (x , y

1 1 2 2

), … , (x

, y

) деякої точної функціональної залежності.

Така постановка завдання часто зустрічається в інженерній практиці,

однак в економічних розрахунках належна увага їй не приділяється.

2. Апроксимовані. У деяких випадках вигляд залежності Y = f(X)

відомий, але через її складність або з інших причин не відповідає

поставленим цілям дослідження. У таких випадках вихідну функцію

замінюють іншою, як правило поліноміальною. Цей процес називаєть-

ся апроксимацією. Нова функція відображає початкову залежність між

ознаками вже неточно. У зв’язку з розширення сфери застосування

комп’ютерів, проблема апроксимації стає все менш актуальною.

3. Нормалізовані. При встановленні залежності

Y = f(X , X , ... , X

) (1.7)

1 2

зазвичай приймається, що результуючий показник залежить лише від

чинників

X , X

1 2

, ... , X

. Однак внаслідок припущення про цілісність

об’єктів, що вивчаються, потрібно вважати, що всі характеристики

економічних об’єктів взаємопов’язані, тому на результат впливає наба-

гато більше чинників, ніж враховано в моделі. Тому виникає необхід-

ність розподілу чинників на “істотні”

, X

, ... , X

, що прямо врахо-

вуються в моделі, і “неістотні”

n + 1

, X

n + 2

, ... , вплив яких доводиться

ігнорувати. Нормалізовані залежності відображають вплив істотних

чинників у припущенні значень неістотних. Як правило, значення цих

чинників вважаюся “середніми” у тому чи іншому сенсі цього слова.

При побудові прогнозного значення результуючого показника нові

значення неістотних чинників стають невідомими і заміна їх на середні

значення негативно впливає на точність прогнозу.

4. Регресійні. В таких залежностях також здійснюється поділ

чинників на істотні та неістотні. Однак вплив неістотних чинників

формалізується шляхом подання як невизначених величини. Тоді їх дія

агрегується в один невизначений чинник

e, який називається помил-

кою спостереження. Задання тоді зводиться до пошуку залежності виду:

Y = f(X , X , ... , X

, e). (1.8)

1 2

Звичайно, при цьому потрібно вводити додаткові припущення

не лише про вид залежності

Y від e, але і про характер невизначеності

e. Найбільш розповсюдженою є імовірнісна формалізація, коли e трак-

тується як випадкова величина з деяким, як правило нормальним, за-

коном розподілу. Залежність у такому випадку записується у вигляді:

Y = f(X , X , ... , X

) + e, (1.9)

1 2

де

e має ненормальний розподіл з нульовим середнім значен-

ням і дисперсією

, X , ... , X

), яка в загальному випадку невідо-

ма, і тому підлягає оцінюванні поряд з самою функцією.

1.4. Основні етапи побудови економетричної моделі

Побудова економетричної моделі – центральна проблема будь-

якого економетричного дослідження, оскільки її якість визначає до-

стовірність та обґрунтованість результатів аналізу розвитку та прогно-

зу соціально-економічних процесів і явищ.

У загальному випадку процедуру побудови економетричної

моделі можна розділити на послідовність взаємопов’язаних етапів:

1. Аналіз специфічних властивостей досліджуваних процесів

та явищ і обґрунтування класу моделей, що є найбільш придатними

для їх опису. На даному етапі потрібно:

− обрати раціональний склад змінних, які увійдуть в модель і

визначити їх кількісні характеристики;

− розбити сукупність об’єктів на однорідні групи;

− обґрунтувати тип і форму моделі, яка виражається мате-

матичним рівнянням.

2. Оцінка параметрів обраної моделі на основі вихідних даних.

3. Перевірка якості побудованої моделі та обґрунтування ви-

сновку щодо її подальшого використання в дослідженнях.

При формуванні вихідної інформації для побудови моделі до-

сить важливим є відбір показників, адекватних сутності досліджуваних

явищ. У ході змістовного аналізу явище часто розглядається на якіс-

ному рівні. Однак при побудові моделі використовуються набори по-

казників, які виражають досліджувані властивості кількісними харак-

теристиками. Тому потрібно, щоб цей вираз був якомога точнішим.

Невірний вибір показників може негативно вплинути на якість

побудованої моделі. Тому проблема відбору “оптимальних” факторів як

правило вирішується на основі змістовного та кількісного аналізів тен-

денцій досліджуваних процесів та явищ. На етапі змістовного налізу

вирішується доцільність включення в модель тих чи інших чинників,

виходячи із “здорового глузду” та даних економічної теорії. Наприк-

лад, побудова функції Кобба-Дугласа здійснюється у припущенні, що

об’єм виробництва в основному залежить від розміру основних фондів

та кількості витраченої праці. Крім того, потрібно врахувати, що одна і

та сама властивість може виражатись декількома чинниками, щільно

пов’язаними між собою. Тому включення їх в модель одночасно є не-

доцільним і навіть необов’язковим, тому що одна і та сама характерис-

тика буде врахована декілька раз.

Кількісний аналіз дозволяє відібрати найбільш підхожі неза-

лежні чинники на основі взаємозв’язку між ними та їх впливу на ре-

зультуючий показник. Як правило, ступінь зв’язку між показниками

може виражатись значенням коефіцієнта кореляції – чим він ближчий

за абсолютним значенням до одиниці, тим зв’язок щільніший. Тому

потрібно відбирати ті чинники, які мають високий коефіцієнт парної

кореляції з результуючим показником, і невисокі між собою. При цьо-

му може виникнути проблема хибної кореляції – високе значення кое-

фіцієнта може визначатись випадковим збігом в тенденціях розвитку

показників при відсутності між ними логічно обґрунтованих взаємо-

зв’язків. Тому при відборі чинників для побудови моделі потрібно до-

тримуватись таких рекомендацій:

1) кількість чинників, що включається в модель, не повинна

бути великою, тому що їх збільшення може виражати не закономірнос-

ті розвитку на фоні випадковості, а саму випадковість;

2) простота моделі в значній степені гарантує її адекватність.

Складна модель може швидше виражати другорядні взаємозв’язки між

змінними замість основних.

Сукупності даних досить часто виявляються неоднорідними.

Наприклад, при вивченні закономірностей, що виявляються в групі

країн або в групі підприємств (нехай навіть однієї і тієї ж самої галузі),

завжди може виявитися, що сукупність складається не тільки з оди-

ниць, що мало відрізняються одна від одної. Так, країни можуть бути

високо- і малорозвинені; а підприємства – або великі та малі, або ті,

що мають сучасне і застаріле технічне оснащення. У подібних випад-

ках було б неправильно виходити з того, що дані відносяться до однієї

і тієї ж самої популяції. Такого роду аналіз необхідний, тому що мож-

на припустити, що в кожній з цих груп досліджувані явища можуть

формуватися інакше і залежати від різних факторів. Єдина функція

регресії, розрахована для всієї сукупності об’єктів, буде описувати

досліджувану залежність найкраще “у середньому”, а картина дійсності,

що вийшла, буде не зовсім правильною, якщо взагалі не перекрученою.

У такому випадку регресійна залежність будується окремо для

кожної однорідної підмножини даних.

Задача вибору підходящої форми функції регресії не становить

особливих труднощів у випадку двовимірних ознак. З уведенням біль-

шого числа пояснюючих змінних істотно збільшуються “масштаби”

труднощів. У цьому випадку вже не можна охарактеризувати якість

побудови функціональної залежності до розподілу емпіричних точок

за допомогою широко розповсюдженої, так званої, візуальної оцінки.

Розглядаючи проблему вибору функціональної залежності,

слід зауважити, що у практиці економетричних досліджень використо-

вується досить широке коло залежностей:

а) лінійна:

eXXXY

...

22110

, (1.10)

б) права напівлогарифмічна:

eXXXY

⋅

ln...lnln

22110

, (1.11)

в) степенева:

eXXXY

+++++α=

αα

...

210

, (1.12)

г) гіперболічна:

eXXXY

+++++α=

αα

/1.../1/1

210

, (1.13)

д) обернена лінійна (функція Торнквіста):

eXXXY

+++++α=

αα

/1.../1/1/1

210

. (1.14)

Більшість функцій шляхом перетворень може бути зведена до

лінійної форми (1.9). Конкретний вигляд функціональної залежності як

правило виражає деяку змістовну концепцію, яка відображає характер

взаємозв’язку між показниками. Наприклад, степенева залежність ґру-

нтується на припущенні про сталість часткової еластичності результу-

ючого показника (наприклад, виробництва) по кожному чиннику (ре-

сурсу). Нагадаємо, що часткова еластичність показує, на скільки відсо-

тків зміниться результуючий показник при зміні чинника на 1 % при

сталих значеннях інших чинників.

Методи оцінювання параметрів моделі залежать від того, яку

саме форму приймає модель. У більшості випадків найбільш пошире-

ним є метод найменших квадратів та його модифікації.

Вибір кращого варіанта економетричної моделі здійснюється

шляхом порівняння відповідних їх якісних характеристик, які обчис-

люються як за вихідними значеннями показників, так і за розрахунко-

вими значеннями, одержаними після побудови моделі. У загальному

випадку якість моделі оцінюється за двома групами характеристик.

Перша містить показники та критерії, що виражають “ступінь” відпо-

відності побудованої моделі основним закономірностям процесу чи

явища, яке вона описує. Сюди можна віднести критерій Стьюдента,

який використовується для оцінки значущості впливу кожного з чин-

ників на результуючий показник. Відповідність моделі процесу можна

оцінити на основі аналізу властивостей помилки

e. Якщо модель пра-

вильна, то значення помилки носять випадковий характер. “Невипад-

ковість” помилки може пояснюватись неправильно обраною формою

моделі, неправильно обраним методом оцінки її параметрів, а також

автокореляцією між сусідніми значеннями помилки.

Друга група містить показники та критерії, що оцінюють точ-

ність її апроксимації спостережених значень результуючого показника

Y. Сюди відносять коефіцієнт множинної кореляції R, коефіцієнт детер-

мінації

D, та критерій Фішера F. Коефіцієнт множинної кореляції по-

казує ступінь наближення розрахованих значень результуючого показ-

ника до його емпіричних значень. Він змінюється в межах від 0 до 1.

Чим ближче його значення до 1, тим краща модель. Коефіцієнт детер-

мінації також змінюється в межах від 0 до 1. Його величина показує

частку мінливості змінної

Y, яка пояснюється включеними у модель

чинниками

. “Вдала” модель повинна пояснювати якомога більшу

частку мінливості. Фактично, коефіцієнт детермінації є універсальним

показником ступеня щільності статистичного зв’язку між чинниками

та змінною Y. Критерій Фішера також використовується для визна-

чення надійності всієї моделі шляхом порівняння міри її помилки з

величиною міри розсіювання значень

відносно середнього значення

. Цей критерій може також виступати для обґрунтування включення

в модель всієї сукупності змінних.

1.5. Якість оцінок параметрів економетричних моделей

Економетрична модель вважається побудованою, якщо визна-

чені її параметри. Таким чином, обчислені значення

, a

, … , a

можна

розглядати як оцінки істинних значень параметрів моделі

, α

, ... , α

залежних загальному випадку від вихідних даних і застосованого ме-

тоду оцінювання. Ці оцінки є випадковими величинами. Їх випадковий

характер можна інтерпретувати наступним чином. Значення побудова-

ної залежності

Ŷ = f(X), одержані при відомому наборі значень a

, a

, … , a

можна розглядати як оцінки, що наближають емпіричні значення

Якість цього наближення, а отже і якість оцінок

, a

, … , a

повин-

на узгоджуватись з властивостями випадкової помилки

= y – ŷ

i i

Таким чином, кожній вибірковій послідовності помилок

ставиться у

відповідність “свій” набір параметрів, і навпаки. Одержану будь-яким

способом оцінку

параметра α

можна розглядати як вибіркову ви-

падкову величину, що являє собою суму істинного значення і помилки:

= α + Δa . (1.15)

i i

Теорія статистичного оцінювання визначає якість оцінок за

властивостями незміщеності, ефективності, асимптотичної незміщенос-

ті, асимптотичної ефективності, змістовності.

Оцінка параметра називається незміщеною, якщо істинне зна-

чення параметра рівне математичному сподіванню оцінки:

M[a ] =

. (1.16)

i i

Іншими словами, математичне сподівання помилки оцінки:

M[Δa ] = 0. (1.17)

Оцінка називається ефективною, якщо вона характеризується

найменшою дисперсією серед інших аналогічних оцінок, одержаних

іншими методами.

Часто властивість незміщеності виконується лише при достат-

ньо великих об’ємах вибірки. У таких випадках говорять про асимп-

тотичну незміщеність. Іноді її виражають у імовірносному вигляді:

1}|{|lim =ε<α−

∞→

, (1.18)

де

P{*} означає імовірність події, обмеженої дужками. Вираз

(1.18) означає, що границя по імовірності від послідовності

дорів-

нює

. Оцінки, мають таку властивість, називаються змістовними.

Вираз (1.18) в літературі часто записується ще таким чином:

.)lim(

aP α= (1.19)

Наявність асимптотичних властивостей в оцінок параметрів

свідчить про їх більш високу якість порівняно з альтернативними варі-

антами оцінок, які такими властивостями не володіють. Можна припу-

стити, що збільшення об’єму вибірки призведе до зменшення похибки

оцінки параметрів. Однак це буде істинним лише у тому випадку, коли

вибірка не втрачає своєї однорідності, тобто, закономірності у збіль-

шеній вибірці відповідають закономірностям початкової.

Таким чином, різні методи визначення параметрів економет-

ричних моделей можуть призводити до оцінок , що відрізняються за

своїми кількісними характеристиками. При цьому погіршення власти-

востей оцінки іноді обумовлюється тим, що застосування того чи ін-

шого методу не відповідають властивостям досліджуваного процесу.

Питання для самоперевірки

1. Що в економетриці розуміють під ознакою?

2. Охарактеризуйте складові економетричної моделі.

3. За якими ознаками можна класифікувати економетричні мо-

делі?

4. Охарактеризуйте основні етапи побудови економетричної

моделі.

5. В чому сутність “хибної кореляції”? Як її уникнути?

6. Як оцінити якість економетричної моделі?

7. Як оцінити якість одержаних параметрів економетричної

моделі?

МЕТОДИ ОЦІНКИ ПАРАМЕТРІВ

ЛІНІЙНИХ ЕКОНОМЕТРИЧНИХ МОДЕЛЕЙ

2.1. Метод найменших квадратів

1. Загальні відомості про застосування методу. Метод най-

менших квадратів (МНК) є одним з найбільш розповсюджених методів

оцінки параметрів лінійної моделі через свою простоту та ефектив-

ність. Він не висуває жорстких вимог до закону розподілу помилок

моделі. Внаслідок цього оцінки коефіцієнтів моделі не залежать від

фактичного або прийнятого закону розподілу. Разом з тим стосовно

помилок

висуваються наступні припущення:

– помилка має нульове математичне сподівання, M[e ] = 0;

– її дисперсія скінчена і стала (хоча і невідома),

σ = const;

– автокореляційні зв’язки в ряду помилки відсутні. Під авто-

кореляцією розуміють зв’язок між значеннями

та “зсунутими” зна-

ченнями

i-j

;

– ряд значень помилки статистично не пов’язаний з рядами

значень незалежних змінних моделі.

Нехай в загальному випадку лінійна модель має вигляд:

eXXXY

...

22110

, (2.1)

або в матрично-векторному вигляді:

eXaY

. (2.2)

Знайдені за допомогою МНК оцінки

a , a

0 1

, … , a

забезпечу-

ють мінімум наступної квадратичної форми на множині всіх інших

комбінацій таких оцінок:

∑∑

α−−α−α−α−==

niniii

xxxyes

22110

)...(

. (2.3)

Для обчислення параметрів моделі потрібно взяти часткові по-

хідні і прирівняти їх до нуля. Тим самим ми одержимо так звану сис-

тему нормальних рівнянь, яка має вигляд:

][][ YXaXX

= . (2.4)

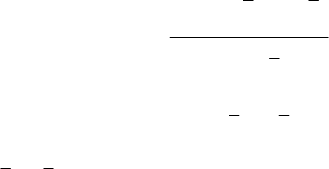
Розв’язавши систему, знайдемо потрібні оцінки параметрів

моделі:

][][

YXXXa

TT −

= . (2.5)

Якщо модель має лише одну незалежну змінну, то для знахо-

дження її параметрів можна скористатись іншими формулами, які є

більш зручними для практичного застосування:

)(

))((

∑

−

−−

xxyy

(2.6)

xaya

−

– відповідні середні. та

де

Отже, за формулою (2.5) вектор параметрів можна одержати

завжди крім випадку, коли матриця

X] є виродженою, а отже обер-

неної до неї не існує. А виродженою матриця буде в одному з двох

випадків:

– коли чинники взаємозалежні (тобто, парні коефіцієнти коре-

ляції між чинниками близькі за абсолютною величиною до 1). Тоді

стовпчики матриці X є лінійно залежними. Цей ефект одержав назву

мультиколінеарності;

– коли кількість спостережень менша за кількість оцінюваних

параметрів моделі (

m < n).Тоді в системі нормальних рівнянь кіль-

кість невідомих більша за кількість рівнянь.

Слід зауважити , що у випадку мультиколінеарності матриця

[

X] може мати властивість поганої обумовленості, тобто, вона буде

“близькою” до виродженої, але не виродженою. Тоді для оцінки пара-

метрів моделі потрібно розв’язати систему нормальних рівнянь виду

(2.4) іншим методом, наприклад, Жордана-Гауса.

Наостанку зазначимо, що оцінки параметрів лінійної моделі,

одержані за допомогою МНК для детермінованих вихідних даних,

будуть мати властивості незміщеності та ефективності.

2. Стохастичні незалежні змінні. Однак в економетричних

дослідженнях в ролі значень чинників доводиться використовувати

дані, які не можна інтерпретувати як детерміновані величини, оскільки

вони є результатами вибіркових спостережень. Прикладами таких да-

них є середній дохід на одну особу, середнє споживання на одну особу

тощо. Їх значення визначаються за деякою вибіркою індивідуумів з

генеральної сукупності мешканців. Аналогічна ситуація може статись,

коли в ролі вихідних даних використовуються значення, що характе-

ризують випадково відібрані елементи генеральної сукупності. Наприк-

лад, серед малих підприємств певної галузі формується вибірка її ха-

рактеристики відібраних підприємств розглядаються як значення чин-

ників. У таких випадках ці знання інтерпретуються як випадкові вели-

чини з певним законом розподілу. Одержані за допомогою МНК оцін-

ки параметрів моделі при цьому будуть володіти лише властивостями

асимптотичної незміщеності та ефективності.

3. Властивості фактичної помилки економетричної моделі. Далі

будуть наведені властивості фактичної помилки

, які завжди вико-

нуються при використання МНК.

1. Сума значень фактичної помилки дорівнює нулю.

∑

−

€

(

iii

yye

. (2.7)

2. Добуток транспонованої матриці спостережень на вектор

фактичної помилки рівний нульовому вектору:

e = 0. (2.8)

Ця властивість свідчить про відсутність кореляційного зв’язку

між чинниками та фактичною помилкою.

3. Сума добутків помилки на відхилення розрахованих значень

результуючого показника від його середнього значення дорівнює нулю:

€

( =

−

∑

yye

. (2.9)

Зазначені властивості випливають безпосередньо з припущень

щодо можливості застосування МНК. Тому їх наявність у фактичної

помилки не є доведенням наявності цих самих властивостей у “істин-

ної” помилки моделі. Однак відсутність якоїсь з цих властивостей свід-

чить про погану якість побудованої моделі.

Перевірку сталості дисперсії помилки моделі можна виконати

за одержаними фактичними значеннями помилки

застосуванням

двостороннього критерію Фішера. В такому випадку інтервал значень

результуючої змінної

Y впорядковується і розбивається на три части-