Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.

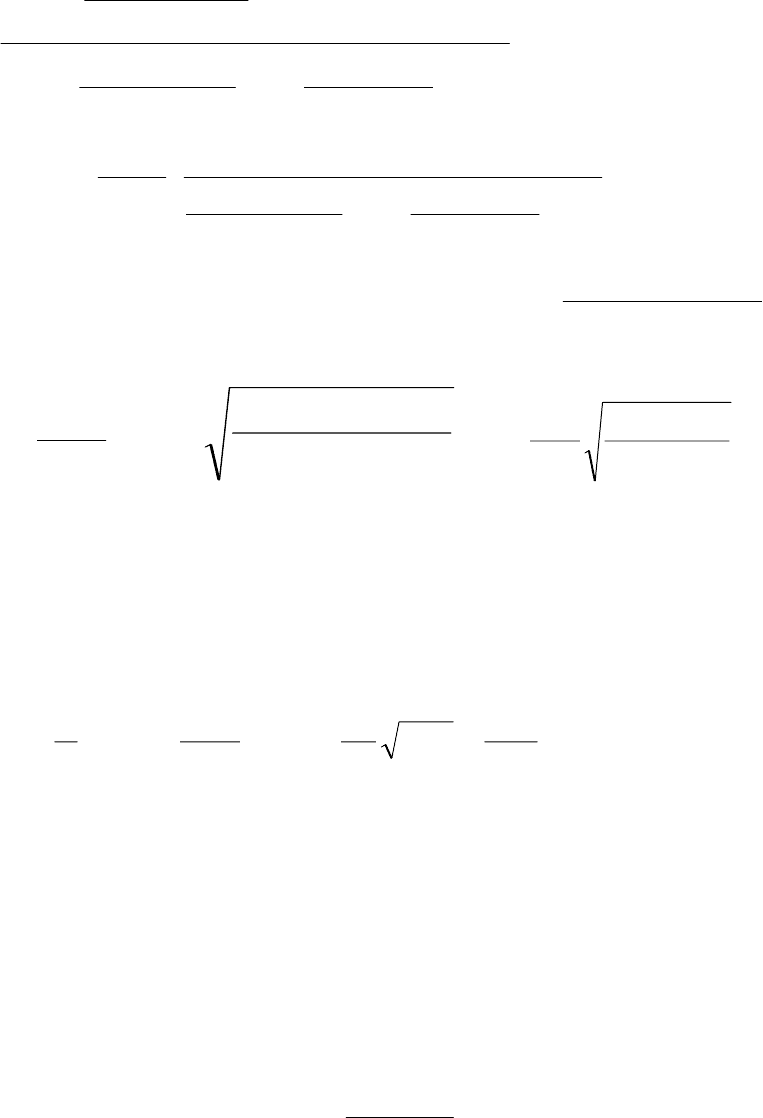
Таким образом, передаточная функция устройства, изображенно-
го на рис. 3.12, а, будет равна
Wp W pW p() () ()=
=
1 экв
()
()
,
12
1
1
1
1
1
22
63
2542
2
6
21542
61
52
63
2542
2
6
21542
63
13
5
2
131
3
+ξ+
=
=
++
⋅=
=
++
+
+
−
=
TppT
k
p
RR
CRRR
p
R
CCRRR
RR
RR
p
RR
CRRR
p
R
CCRRR
RR
pCRRR
pCRR
R
где
61
52
RR
RR
k =
,
6
21542
R
CCRRR
T =
,
26
1542
3
2
1
CR
CRRR
R
=ξ
.
Рассмотренное устройство позволяет легко реализовать как ко-
лебательное, так и апериодическое звено второго порядка. Если, на-
пример, принять
CCCRRRR
=
=
=
=
=
21652
,
, то при известных
значениях
T
k
, и
ξ
можно определить номиналы остальных элемен-
тов:
C
T
RRR
R
C
T
R
R
k
R
ξξ
22
1
, ,
43
2
2
41
==== . (3.5)
3.2.2.3. Консервативное звено
Это звено получается при мнимых полюсах передаточной функ-
ции (3.1) и его можно рассматривать как частный случай колебатель-
ного звена при
0=
ξ
. Выражения для передаточной и некоторых
частотных функций звена будут иметь вид:
1
)(
22
+
=
pT
k
pW
,

22
1
)(
T
k
jW
ω
−
=ω ,
22
1
)(
T
k
A
ω−
=ω
,
22
1lg20lg20)( TkG ω−−=ω .
≥ωπ−
<ω
=
ω−
ξω
−=ωϕ
→ξ
.
1
,
1
0
1
2
arctglim)(
при
при
22
0
T
T
T
T
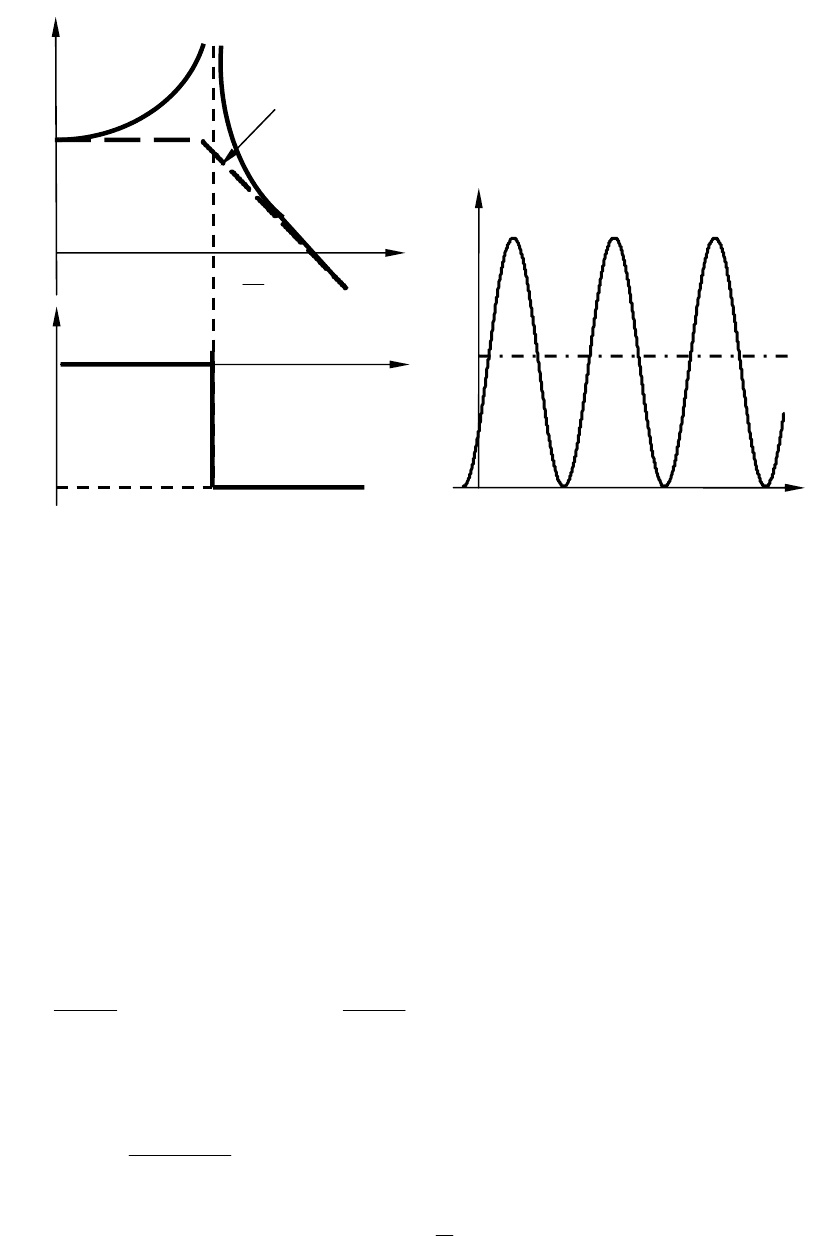
На рис. 3.13,
а изображены логарифмические частотные характе-
ристики консервативного звена. Точная ЛАЧХ (сплошная линия)
терпит разрыв непрерывности второго рода на частоте сопряжения
T
1
c
=
ω
, асимптотическая ЛАЧХ (пунктирная линия) такая же, как у
колебательного звена. ЛФЧХ в точке
c
ω
терпит разрыв непрерывно-
сти первого рода (фаза скачком изменяется от 0 до
π
−
).
Переходная функция консервативного звена может быть получе-
на по формуле (2.10) при мнимых полюсах
T
j
p ±=
2,1
и имеет вид
−=
T
t
kth cos1)(
.
На рис 3.13,
б показана переходная характеристика консерватив-
ного звена, она представляет собой незатухающие автоколебания
частотой
T
1
и амплитудой
k
.
Консервативное звено на пассивных четырехполюсниках не реа-
лизуется.
Если обратиться к приведенному выше примеру (см.
рис.2.6), то должны отсутствовать потери в контуре, т.е. выполняться
условие
0
1
=R , что физически невозможно. В устройстве, схема ко-
торого приведена на рис.3.12,
а, в соответствии с формулами (3.5)
получение консервативного звена возможно при
∞=
3
R . Для этого
резистор
3
R просто нужно удалить из устройства.
3.3. Особые звенья линейных САУ
3.3.1 Неминимально-фазовые звенья
В ряде устройств, например, при мостовых соединениях, процес-
сы описываются дифференциальным уравнением, имеющим отрица-
тельные коэффициенты в правой части:
−=+
dt
tdx
txkty
dt
tdy
T
)(
)()(
)(
τ
.
Передаточная функция такого звена будет иметь вид
1
)1(
)(
+
−
=
Tp
pk
pW
τ
,
т.е. имеет положительный нуль
τ
1
0
=p .
Такие звенья относятся к устойчивым неминимально-
фазовым звеньям первого порядка, их характеристики похожи на ха-
рактеристики инерционного форсирующего звена.
Рис.3.13. ЛАЧХ, ЛФЧХ (а), переходная характеристика (б)
консе
р
вативного звен
а
h(t)
k
0 t
б
G(ω)
- 40 дБ/дек
G
0
0
T
1
lg
lgω
ϕ(ω) lgω
π−
а
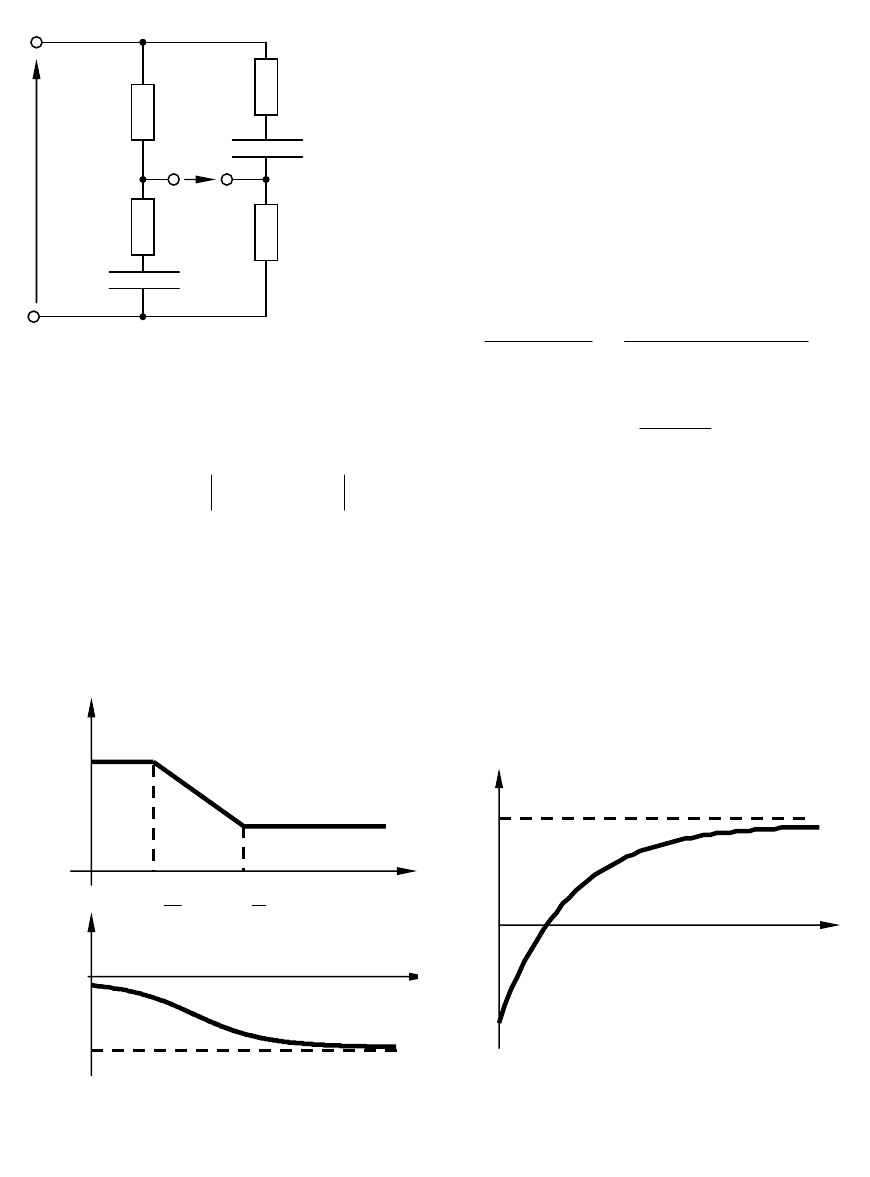
Пример 3.4.
На рис. 3.14 приведена мостовая
схема, в которой выполняется соотно-
шение
12
RR >> . Для нее будет иметь
место соотношение:
(
)
[
]
()
[]
),(1
)(1
вых21
вх21
pUCpRR
pUCpRR
+−=
=
+
+
т.е.
(
)
()
,
1
1
1
1
)(
)(
)(
21
21
вх
вых
Tp
p
k
CpRR
CpRR
pU
pU
pW
+
τ−
=
=
++
+−
==
где
()
(
)
CRRTCRRk
2121
, ,1
+
=
−=
τ
=
.
На рис. 3.14,
а показаны логарифмические частотные характери-
стики этого звена при
1>
k
. Его ЛАЧХ не отличается от ЛАЧХ
инерционного форсирующего звена при
T
<
τ
, а ЛФЧХ изменяется в
диапазоне
π
ϕ
−>>0 . Переходная характеристика (рис.3.14, б) име-
ет при
0=
t
скачок в отрицательном направлении.
Неустойчивые неминимально-фазовые звенья содержат в
передаточных функциях положительные полюсы. Примером такого
звена может служить асинхронный двигатель, работающий в режиме
максимального скольжения. Другой пример – охват минимально-
фазового звена положительной обратной связью.
R
2 R1
С
u
вх
u
вых
R1 R2
С
Рис.3.14. Пример
неминимально-фазового
у
стойчивого звена
G(ω)
G
0
0
T
1
lg
τ
1
lg
lgω
ϕ(ω)
0 lg
ω
π
−
а
h(t)
k
0
t
τ
k
−
б
Рис.3.15. Характеристики устойчивого неминимально-фазового звена
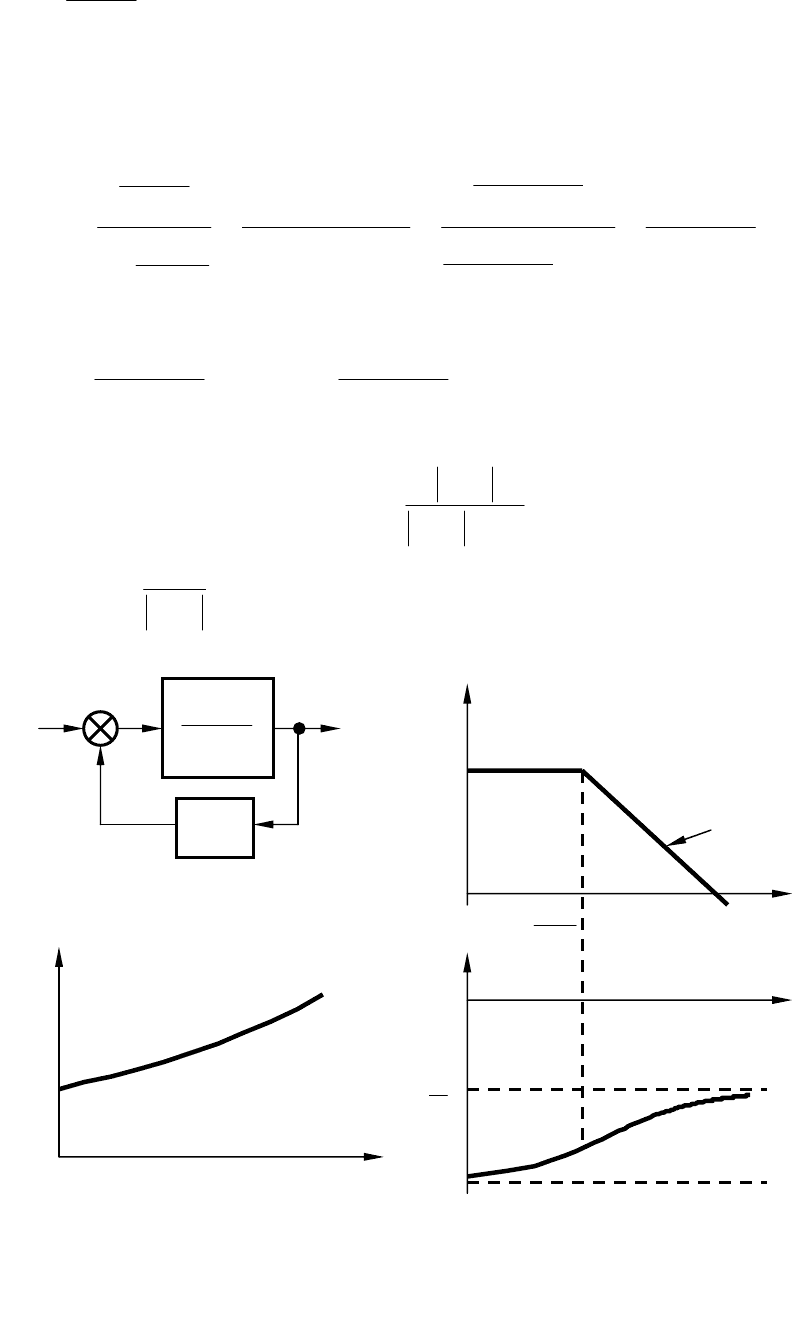
Пусть инерционное звено с передаточной функцией
1
)(
+
=
Tp
k
pW
охвачено положительной обратной связью с коэффи-
циентом передачи
oc
k (рис.3.16, а). Передаточная функция получив-
шегося эквивалентного звена будет иметь вид:
1T
1
1
1
1
1
1
1
)(
экв
экв
oc
oc
oc
oc
экв
+
=
+
⋅−
⋅−
=
⋅−+
=
+
⋅
−
+
=
p
k
p
kk
T
kk
k
kkTp
k
Tp
kk
Tp
k
pW
,
где
oc
экв
oc
экв
1
,
1 kk
T
T
kk
k
k
⋅−
=
⋅−
=
.
При
1
oc
>⋅ kk
величины
эквэкв
, Tk
становятся отрицательными
и передаточная функция
1T
)(
экв
экв
экв
−
=
p
k
pW
становится такой, что
ее полюс
экв
1
T
1
=p
будет положительным.
x y
a
1+Tp
k
oc
k
h(t)
2
k
0
t
б
G(
ω
)
G
0
-20 дБ/дек
0 lg
ω
экв
1
lg
T
ϕ(ω)
0
lgω
1
2
π
−
π
−
в
Рис.3.16. Неустойчивое неминимально-фазовое звено (а) и его
характеристики (
б, в)

На рис. 3.16, б приведена переходная характеристика этого звена,
она неограниченно нарастает, начиная со значения
k
h 2)0( =
, по-
скольку рассчитывается по формуле
+=
T
t
ekth 1)(
. ЛАЧХ неус-
тойчивого неминимально-фазового звена такая же, как и у инерцион-
ного звена, а ЛФЧХ, рассчитываемая по выражению
T
ω
π
ω
ϕ
arctg)( +−= , возрастает со значения
π
−
до
2
π
− (см. рис.
3.16,
в).
3.3.2. Звено чистого запаздывания.
Это звено относится к трансцендентным, его передаточная функ-
ция имеет вид:
.)(
τ
−
=
p
kepW
Получим расчетные формулы для частотных характеристик зве-
на:
[
]
)sin()cos()( ωτ−ωτ==ω
ω
τ
−
jkkejW
j
,
)sin()( ),cos()(
ω
τ
−
=
ω
ω
τ=ω
k
Q
k
P
,
,)(sin)(cos)(
22
kkA =ωτ+ωτ=ω
[]
.)tg(arctg
)cos(
)sin(
arctg)( ωτ−=ωτ−=
ωτ
ω
τ
−
=ωϕ
Годограф АФЧХ (рис.3.17,
а) представляет собой окружность ра-
диуса
k
с центром в начале координат. АЧХ (а, следовательно, и
ЛАЧХ) звена чистого запаздывания такая же, как у пропорциональ-
ного звена. ФЧХ
)(
ω
ϕ
линейно убывает с ростом частоты, а ЛФЧХ
(рис.3.17,
б) криволинейна за счет логарифмического масштаба по
оси
ω
.
Звено чистого запаздывания без искажения воспроизводит на вы-
ходе входную величину, как и идеальное пропорциональное звено,
но с той разницей, что выходная величина запаздывает относительно
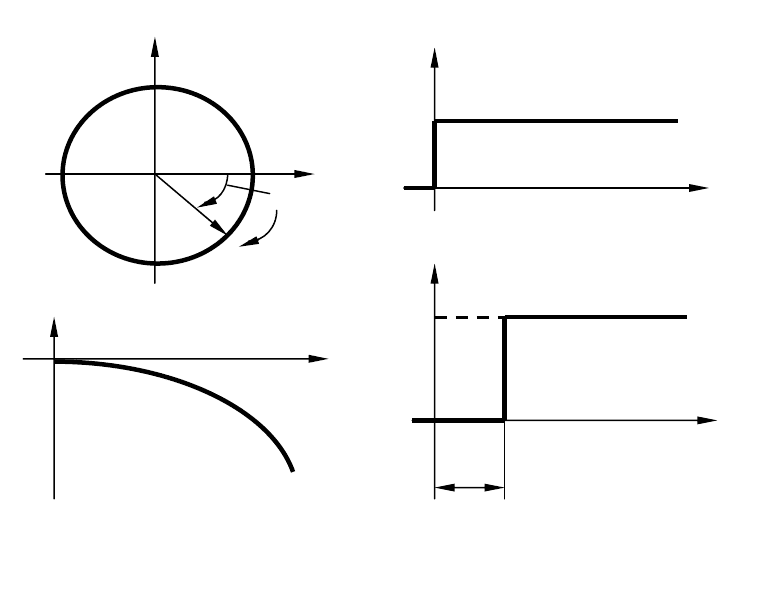
входной на постоянное время
τ
(см. рис.3.17, в, г). Переходная функ-
ция такого звена имеет вид:
)(1)( τ−⋅=
t
k
t
h .
В качестве примера звеньев чистого запаздывания можно назвать
длинную электрическую линию без потерь, механические устройст-
ва, имеющие люфты и т.д.
4. УСТОЙЧИВОСТЬ САУ
4.1. Передаточные функции линейных непрерывных
САУ
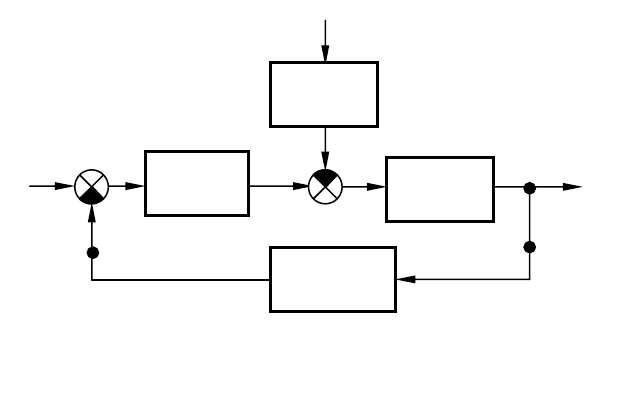
На рис. 4.1 приведена структурная схема простейшей однокон-
турной САУ. Ее можно получить, преобразуя структуру заданной
системы по правилам, приведенным в разделе 2.5 и в соответствую-
щей литературе.
P(ω)
k
-k k Q
(ω)
ϕ(ω)
ω
а
ϕ(ω)
0
lgω
б
1(t)
1
0
t
в
h
(t)
k
0 t
τ
г
Рис.3.17. Частотные (а, б) и временные (в, г) характеристики
звена чистого запаздывания
В соответствии с принципом суперпозиции, справедливым для
линейных непрерывных САУ, данная система характеризуется сле-
дующими передаточными функциями:
4.1.1. Передаточная функция разомкнутой
системы по задающему воздействию
)(
рg
pW . Ее
можно получить, разомкнув САУ в точке 1 и положив
0=
f
, тогда
)()()()(
21рg
1
pWpWp
i
WpW
k
i
⋅==
∏
=
,
где
k
- количество звеньев, расположенных между точкой приложе-
ния задающего воздействия и выходом САУ.
4.1.2. Передаточная функция разомкнутой
системы по возмущающему воздействию
)(
рf
pW
. Ее получают аналогично, размыкая САУ в точке 1 при
0=g
:
)()()(
32рf
1
)( pWpWpW
m
i
p
i
W ⋅==
∏
=
,
где
m - количество звеньев, расположенных между точкой приложе-
ния возмущающего воздействия и выходом САУ.
f
g y
2 1
Рис.4.1. Структурная схема одноконтурной САУ
W
1
(p)
W
ОС
(p)
W
3
(p)
W
2
(p)

4.1.3. Передаточная функция разомкнутой
цепи
)(
рц
pW . Эта передаточная функция получается при размы-
кании системы в точке 2 и обхода всего контура регулирования от
точки приложения задающего воздействия до точки 2. Тогда
)()()()()()(
ос21осрgрц
pWpWpWpWpWpW
⋅
⋅
=
⋅= .
4.1.4. Передаточная функция замкнутой сис-
темы по задающему воздействию )(
зg
pW . В соот-
ветствии с правилом охвата звена отрицательной обратной связью,
получим:
,
)(
)(
)()()(1
)()(
)(1
)(
)(
)(1
)(
)()(1
)(
)(
ос21
21
рц
ос
рц
рц
рg
осрg
рg
зg
pA
pB
pWpWpW
pWpW
pW
pW
pW
pW
pW
pWpW
pW
pW
=
⋅⋅+
⋅
=
=
+
=
+
=
⋅+
=
где
01
1
1
)( bpbpbpbpB
m
m
m
m
++⋅⋅⋅++=
−
−
– полином числителя
передаточной функции,
01
1
1
)( apapapapA
n
n
n
n
++⋅⋅⋅++=
−
−
– характеристический
полином САУ, причем
mn ≥ .
4.1.5. Передаточная функция замкнутой сис-
темы по возмущающему воздействию )(
зf
pW .
Аналогично рассуждая, получим
)(
)(
)(1
)(
)()(1
)(
)(
рц
рf
осрg
рf
зf
pA
pC
pW
pW
pWpW
pW
pW =
+
=
⋅+
=
,
где
01
1
1
)( cpcpcpcpC
r
q
r
q
++⋅⋅⋅++=
−
−
– полином числителя
этой передаточной функции, причем также
r
n ≥ .
Следует отметить, что передаточные функции разомкнутой сис-
темы
)(
рg
pW и )(
рf
pW самостоятельного значения не имеют, в то
время как остальные передаточные функции играют существенную
роль при исследовании характеристик САУ.
