Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.


Для случая обратной связи при выводе эквивалентной передаточ-
ной функции замкнутого участка
)(
э
pW используем обозначения,
приведенные на рис.2.10, в.
Обратная связь называется отрицательной, если
)()()(
oc
txtxt
−
=
ε
,
как показано на схеме, и положительной, если
)()()(
oc
txtxt
+
=
ε
.
Если
{}
)()( txpX L= ,
{
}
)()( typY L
=
,
{}
)()( tpE ε= L ,
{}
)()(
ococ
txpX L= , то в случае отрицательной обратной связи с уче-
том указанных направлений распространения сигналов получим:
[
]
[]
),()()()(
)()()()()()(
1oc
1oc1
pWpWpYpX
pWpXpXpWpEpY
⋅⋅−=
=
⋅
−
=
⋅
=
или
)()()()()()(
11oc
pWpXpWpWpYpY
⋅
=
⋅
⋅
+ .
Отсюда получаем передаточную функцию
)()(1
)(
)(
)(
)(
1oc
1
э
pWpW
pW
pX
pY
pW
⋅+
==
.
Для положительной обратной связи в знаменателе формулы знак
“плюс” меняется на “минус”.
Указанные три вида преобразования структурных схем являются
наиболее часто встречающимися. Для остальных случаев сформули-
руем основной принцип преобразования и поясним несколькими
примерами. При преобразовании структурной схемы передача сигна-
ла по выбранному направлению не должна меняться.
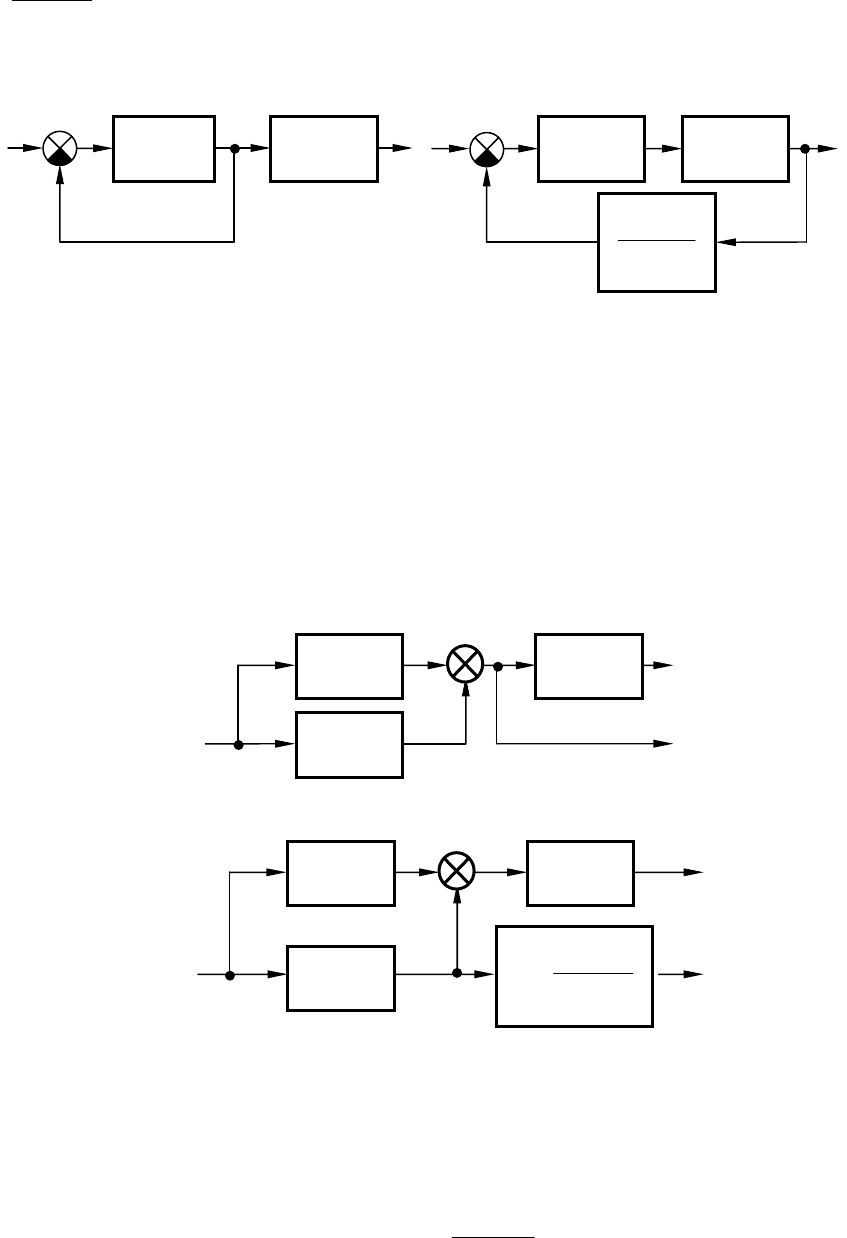
Например, в структурной схеме на рис.2.11, а необходимо пере-
нести узел через звено с передаточной функцией
)(
2
pW .
Чтобы передача сигнала по цепи обратной связи не изменилась,
необходимо ввести фиктивное звено с передаточной функцией
)(
1
2
pW
, как показано на рис.2.11, б.
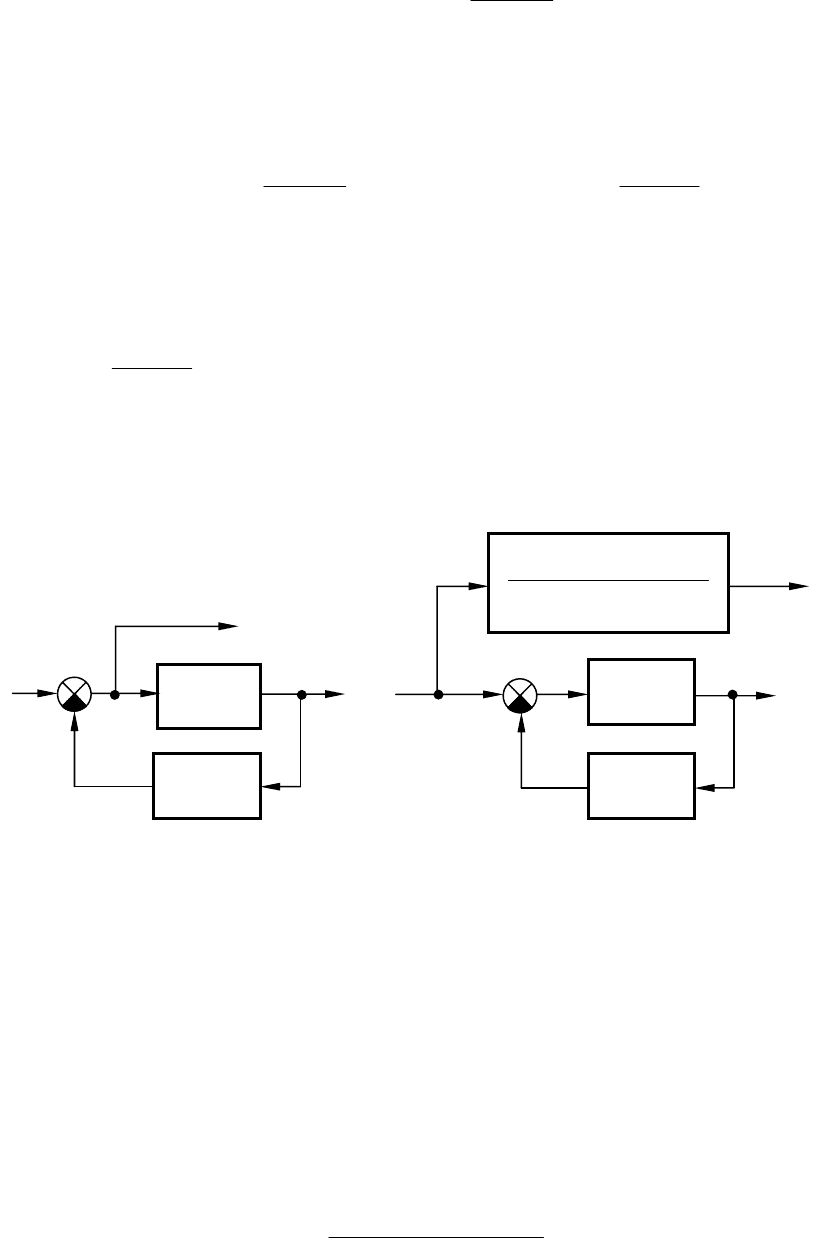
В более сложных случаях в процессе преобразования необходимо
производить определенные расчеты. Например, в схеме на рис.2.12, а
узел 1 необходимо перенести на выход звена с передаточной функ-
цией
)(
2
pW
.
Установим связь между величинами
)(
p
Y
и )(
2
pX .
На входе звеньев с передаточными функциями
)(
1
pW и )(
2
pW
действует сигнал
)(
)(
)(
2
2
pW
pX
pX =
.
На выходе звена с передаточной функцией
)(
1
pW
а б
Рис.2.11. Преобразование структурной схемы (пример 1)
W
1
(p) W
2
(p) W
1
(p) W
2
(p)
)(
1
2
pW
x
1
1
x x
2
y
a
x
1
x x
2
y
б
Рис. 2.12. Преобразование структурной
схемы (пример 2)
)(
)(
1
2
1
pW
pW
+
W
1
(p)
W
2
(p)
W
3
(p)
W
1
(p)
W
2
(p)
W
3
(p)
)(
)(
)(
)()()(
1
2
2
11
pW
pW
pX
pWpXpX ⋅=⋅=
.
На выходе сумматора в узле 1
+⋅=⋅+=
)(
)(
1)()(
)(
)(
)()(
2
1
211
2
2
2
pW
pW
pXpW
pW
pX
pXpY
.
Отсюда видно, что в рассматриваемом примере при переносе узла
необходимо ввести фиктивное звено с передаточной функцией
)(
)(
1)(
2
1
pW
pW
pW +=
, как показано на рис. 2.12, б.
При переносе узла в схеме на рис.2.13, а с выхода сумматора на
его положительный вход найдем передаточную функцию фиктивного
звена без дополнительных пояснений.
{}
{
}
,)()( ,)()( tpEtxpX
ε
LL
=
=
{
}
)()(
ococ
txpX L
=
,
),()()(
oc
pXpXpE
−
=
),()()()(
oc1oc
pWpWpEpX
⋅
⋅
=
),()()()()(
oc1
pWpWpEpXpE
⋅
⋅
−
=
)()(1
)(
)(
oc1
pWpW
pX
pE
⋅+
=
.
ε
ε
x y x y
x
oc
x
oc
а б
Рис.2.13. Преобразование структурной схемы (пример 3)
W
1
(p)
W
ос
(p
)
W
1
(p)
W
ос
(p)
)()(1
1
oc1
pWpW+

3. ТИПОВЫЕ ЗВЕНЬЯ САУ
3.1. Понятие типового звена. Классификация типо-
вых динамических звеньев САУ
В общем случае какой-либо объект в теории автоматического
управления описывается передаточной функцией, содержащей поли-
номы от
p
произвольного порядка в числителе и знаменателе. Но
если передаточная функция объекта содержит только простой мно-
житель в числителе (знаменатель при этом представляет собой дейст-
вительное число) либо только простой множитель в знаменателе
(числитель представляет собой действительное число), то объект на-
зывается
типовым динамическим звеном (или просто типовым зве-
ном).
Из курса алгебры известно, что полином любого порядка можно
разложить на простые множители. То есть любую САУ можно пред-
ставить в виде последовательного соединения типовых звеньев. С
другой стороны, реальные звенья САУ могут иметь самую разнооб-
разную физическую основу (электронные, механические, гидравли-
ческие, электромеханические и т.п.) и конструктивное выполнение,
но иметь одинаковые передаточные функции и являться одинаковы-
ми типовыми звеньями. Поэтому знание характеристик звеньев столь
же необходимо для расчетов в ТАУ, как знание таблицы умножения в
арифметике.
Все линейные типовые звенья условно разделяют на три группы.
В зависимости от характера нулей или полюсов передаточной функ-
ции. Поэтому различают:
- Минимально- фазовые звенья. Передаточные
функции этих звеньев могут содержать в своей структуре как нули,
так и полюсы, причем полюсы могут иметь отрицательные вещест-
венные части, быть нулевыми или чисто мнимыми. Поэтому фазовая
характеристика таких звеньев изменяется в диапазоне
2
)(
π
ωϕπ
<≤−
или от -180° до 90°. Среди минимально фазовых
звеньев иногда выделяют позиционные звенья, которые харак-
теризуются тем, что в каждом из них, кроме консервативного, при
подаче на вход постоянной величины с течением времени устанавли-
вается постоянное значение выходной величины.
- Неминимально- фазовые звенья. Их передаточ-
ные функции имеют нули (устойчивые звенья) или полюсы

(неустойчивые звенья), расположенные в правой комплексной
полуплоскости.
- Звенья с распределенными параметрами.
Среди этих звеньев выделяют трансцендентные и ирра-
циональные звенья. В звеньях с распределенными параметрами
количество нулей и полюсов в передаточных функциях может стре-
миться к бесконечности. Передаточные функции трансцендентных
звеньев представляют собой трансцендентные выражения (пример –
звено чистого запаздывания, являющееся предметом нашего даль-
нейшего рассмотрения), а передаточные функции иррациональных
звеньев описываются иррациональными выражениями (примерами
таких звеньев могут служить различные тепловые и диффузионные
объекты, в частности, радиационная печь, передаточная функция ко-
торой имеет вид
p
k
pW
=)( ).
Трансцендентные и иррациональные звенья часто относят к осо-
бым звеньям линейных САУ, анализ динамических свойств таких
систем требует рассмотрения вспомогательных вопросов.
3.2. Минимально-фазовые звенья
3.2.1 Звенья первого порядка
Звенья первого порядка содержат только один нуль или полюс в
своих передаточных функциях или вовсе не содержат таковых.
3.2.1.1. Пропорциональное (безынерционное)
звено
Описывается уравнением и имеет передаточную функцию
)()(
t
x
k
t
y
⋅
=
,
.)(
k
p
W
=
Параметр в общем случае
k
называется коэффициентом пере-
дачи
звена и может иметь любую размерность. В частных случаях,
когда
k
является величиной безразмерной, принято пользоваться
термином “коэффициент усиления”.
Частотные и временные функции звена:
,)()()(
k
P
A
j
W
=
ω
=
ω
=
ω

,0)(
=
ω
ϕ
,0)(
=
ω
Q
,lg20)(
k
G
=
ω
)()(
t
t
w
δ
=
.
Примерами таких звеньев могут служить механические связи,
электронные усилители сигналов на низких частотах и др.
Схема на рис.2.7, б, если
1вх
)( RpZ
=
и
2oc
)( RpZ
=
, также будет
являться пропорциональным звеном, поскольку
1
2
)(
R
R
pW −= .
3.2.1.2. Интегрирующее (идеальное) звено
Уравнение и передаточная функция звена:
∫
=
t
dttxkty
0
)()( ,
.)(
p
k
pW =
В случае интегрирующего звена параметр
k
является коэффици-
ентом передачи звена по скорости, численно равным скорости изме-
нения выходной величины при единичном значении входной величи-
ны.
Частотные и временные функции звена:
,)(
ω
−=ω
k
jjW ,0)(
=
ω
P
,)(
ω
−=ω
k
Q ,)(
ω
=ω
k
A
,
2
)(
π
−=ωϕ
,lg20lg20)( ω
−
=
ω
k
G
,)(
t
k
t
h
⋅
=
.)(
k
t
w
=

Построенные по указанным функциям характеристики звена изо-
бражены на рис. 3.1.
Схема на рис.2.7, б будет являться интегрирующим звеном, если
RpZ =)(
вх
, а цепь обратной связи организована конденсатором
(рис. 3.1, е), т.е.
Рис. 3.1. Частотные (а – в), временные (г, д) характеристики
интегрирующего звена и его реализация на операционном
у
силителе
(
е
)
P(
ω
)
0 Q(
ω
)
ω
а
A(
ω
)
0
ω
б
G(
ω
)
20lgk 20 -20 дБ/дек
0 1 lg
ω
ϕ
(
ω
)
0 lg
ω
2
π
−
в
h(t) w(t)
k
α =arctg k
0 t 0 t
г д
C
R
е

Cp
pZ
1
)(
oc
=
.
На самом деле, согласно формуле (2.8) передаточная функция
схемы будет иметь вид
,
11
)(
p
k
TpRCp
pW −=−=−=
где
RC
T
k
11
==
.
При использовании в рассматриваемой схеме реального операци-
онного усилителя переходная характеристика не может иметь значе-
ния, превышающие напряжение питания. Но если предположить
операционный усилитель идеальным, то и реализованное здесь ин-
тегрирующее звено будет идеальным.
3.2.1.3. Дифференцирующее (идеальное) звено
Уравнение и передаточная функция звена:
,
)(
)(
d
t
tdx
kty
=
.)( p
k
pW
⋅
=
Выходная величина пропорциональна скорости изменения вход-
ной величины.
Если входная и выходная величины имеют одинаковую размер-
ность, то коэффициент
k
измеряется в секундах. В этом случае его
принято обозначать через
T
и называть постоянной времени диффе-
ренцирующего звена.
Выражение для основных функций:
,)(
ω
=
ω
jk
j
W
,0)(
=
ω
P
,)(
k
Q
ω
=
ω
,)(
k
A
ω
=
ω
,
2
)(
π
=ωϕ ,lg20lg20)(
ω
+
=
ω
k
G
).()(
t
t
h
δ
=
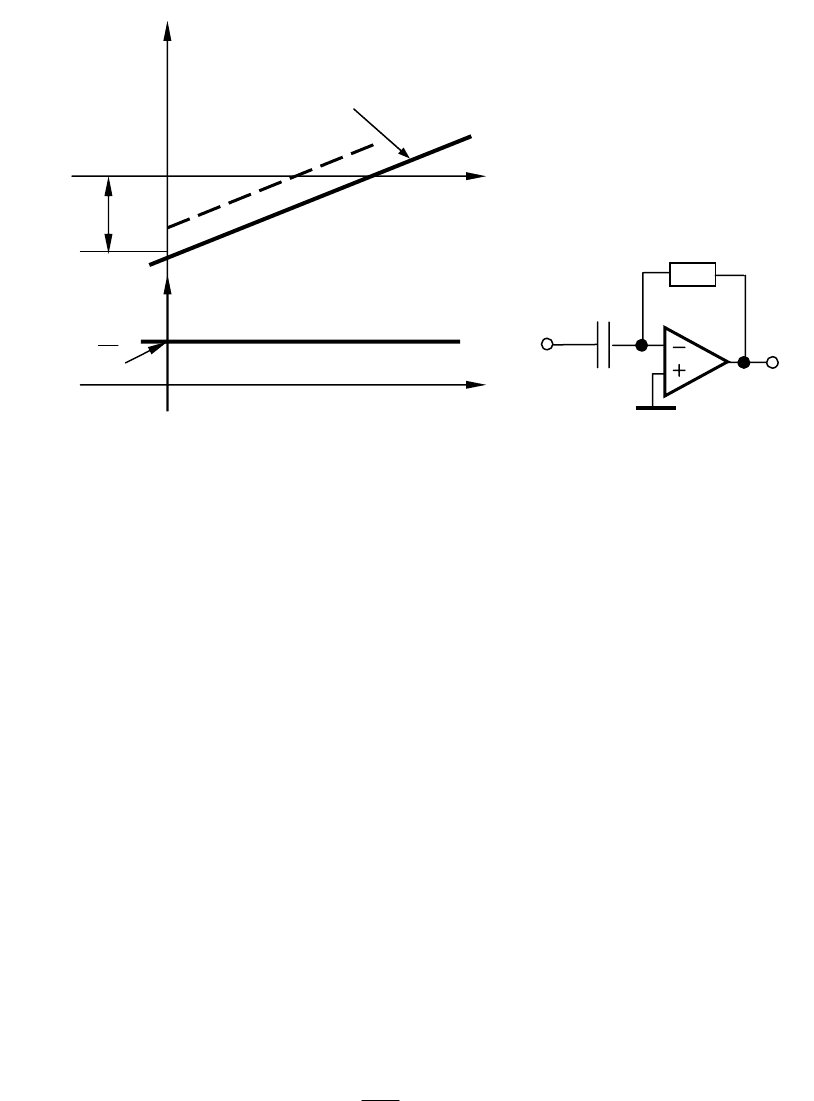
Как передаточная функция, так соответственно и частотные ха-
рактеристики дифференцирующего звена обратны передаточной
функции и соответствующим характеристикам интегрирующего зве-
на.
Логарифмические частотные характеристики рассматриваемого
звена приведены на рис.3.2, а.
При построении ЛАЧХ удобно отложить точку с координатами
1lg =ω , провести через нее прямую с наклоном плюс 20 дБ/дек, за-
тем отложить на оси
)(ω
G
отрезок kG lg20
0
=
(поскольку, как пра-
вило,
,1<
k
точка
0
G будет находиться ниже оси ωlg ) и провести
параллельную прямую.
О том, что звено с представленным математическим описанием
является идеальным, говорит, к примеру, переходная функция. Ни в
каком реальном устройстве невозможно получить мгновенный ска-
чек выходной величины бесконечной амплитуды.
Реальные дифференцирующие звенья обладают конечной инер-
ционностью, вследствие чего осуществляемое ими дифференцирова-
ние не является точным. На рис.3.2, б изображен вариант реализация
дифференцирующего звена ни операционном усилителе с конденса-
тором
C
во входной цепи и резистором R в цепи обратной связи.
Тогда
Cp
pZ
1
)(
вх
= , RpZ
=
)(
ос
,
Рис. 3.2. Частотные характеристики (а) дифференцирующего
звена и его реализация на операционном усилителе (б)
G(
ω
)
+20дБ/дек
0 1 lg
ω
20lgk -20
ϕ(
ω
)
+
π
2
0 lg
ω
а
R
C
б

kpTpRCp
pZ
pZ
pW −=−=−=−=
)(
)(
)(
вх
oc
.
Неидеальность реализации звена определена напряжением пита-
ния усилителя, его выходное напряжение будет конечной величиной.
3.2.1.4. Инерционное звено (апериодическое
звено первого порядка)
Описывается дифференциальным уравнением
).()(
)(
tkxty
d
t
tdy
T
=+
Перейдя к изображениям, получим:
)()()1(
p
k
X
p
Y
Tp
=
+
,
Передаточные и частотные функции:
;
1)(
)(
)(
+
==
Tp
k
pX
pY
pW
;
1
)1(
)1)(1(
)1(
1
)(
22
T
Tjk
TjTj
Tjk
Tj
k
jW
ω+
ω−
=
ω−ω+
ω
−
=
+ω
=ω
;
1
)(Re)(
22
T
k
jWP
ω
+
=ω=ω
;
1
)(Im)(
22
T
kT
jWQ
ω
+
ω
−=ω=ω
;
1
)(
22
T
k
A
ω+
=ω
;arctg
)(
)(
arctg)( T
P
Q
ω−=
ω
ω
=ωϕ
.1lg20lg20)(lg20)(
22
TkAG ω+−=ω=ω
Ни рис. 3.3 приведены основные частотные характеристики инер-
ционного звена. Годограф АФЧХ (рис.3.3, а) имеет вид полуокруж-
ности радиуса
2
k
с центром в точке
0,
2
j
k
, расположенной в чет-
вертом квадранте комплексной плоскости. АЧХ (рис. 3.3, б) моно-
