Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления
Подождите немного. Документ загружается.

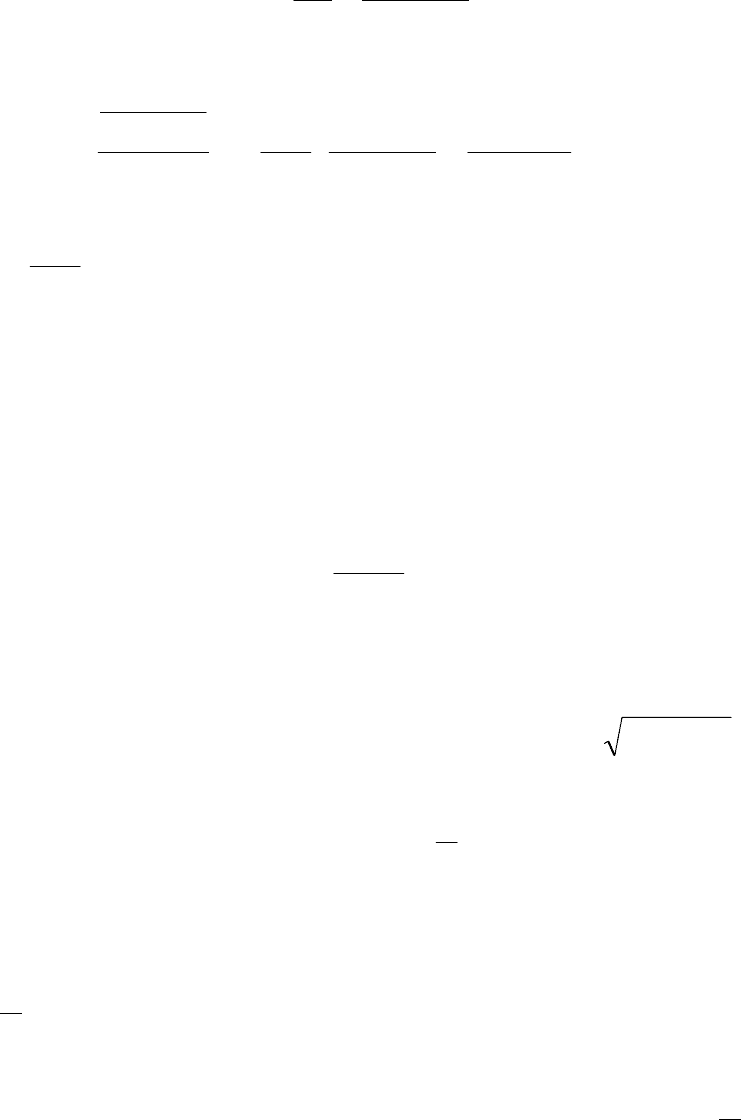
На рис. 3.7, в приведена реализация изодромного звена на опера-
ционном усилителе. Для такой схемы
Cp
CpR
Cp
RpZRpZ
11
)( ,)(
2
2ос1вх
+
=+== . Передаточная функция
()
p
pk
p
CpR
CRR
Cp
CpR
pW
111
1
)(
2
11
2
+τ
=
+
⋅−=
+
−=
,
где
CR
k
1
1
=
, CR
2
=
τ
.
3.2.1.8. Реальное дифференцирующее звено
Такое звено является последовательным соединением дифферен-
цирующего и инерционного звеньев, его передаточная функция
имеет вид
1
)()()(
индифф
+
=⋅=
Tp
kp
pWpWpW
.
ЛАЧХ и ЛФЧХ складываются, т.е.
1lg20lg20lg20)()()(
22
индифф
+−+=+= TkGGG
ωωωωω
,
()
T⋅−=+=
ω
π
ωϕωϕωϕ
arctg
2
)()()(
индифф
.
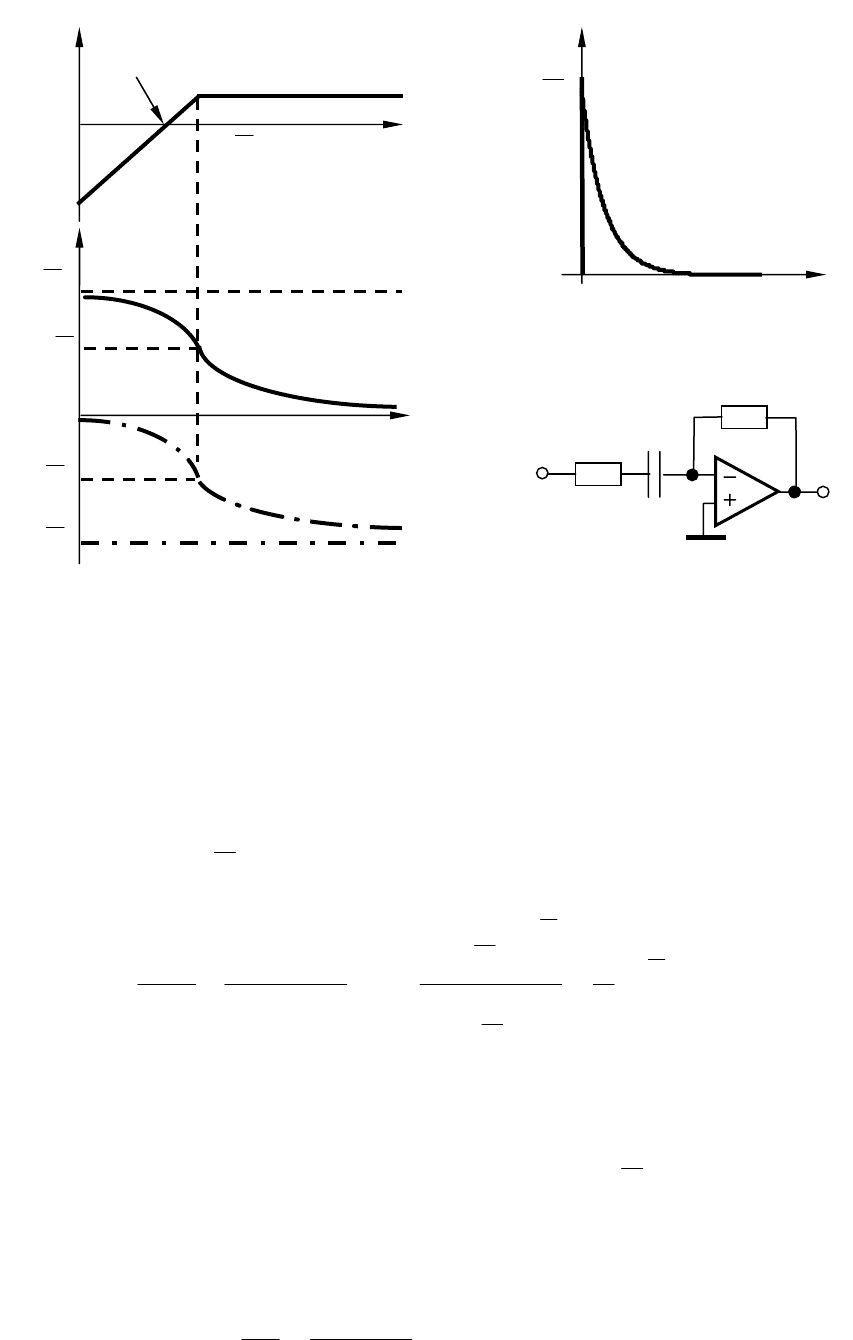
На рис. 3.8 а, приведены логарифмические частотные характери-
стики реального дифференцирующего звена. До частоты сопряжения
T
1
c
=ω ЛАЧХ проходит с наклоном +20 дБ/дек, а после нее – гори-
зонтально. Суммарная ЛФЧХ представляет собой ЛФЧХ инерци-
онного звена, смещенную за счет интегрирующего звена на угол
2
π
.
Расчетное выражение для переходной функции этого звена может
быть получено по формуле (2.14) при
kpp
B
=
)( , 1)(
+
= Tpp
A
,
T
p
A
=
′
)(
,
T
p
1
1
= :
T
t
T
t
tp
e
T
k
T
T
e
T
k
pAp
epB
A
B
th
−
−
=
−
−
+=
′
+=
1
1
0
)(
)(
)0(
)0(
)(
11
1
1
.
На рис.3.8, б приведена переходная характеристика звена. Она
спадает по экспоненте до нуля от значения
T
k
h =)0(
.
На рис. 3.8, в приведена реализация реального дифференцирую-
щего звена на операционном усилителе. Для такой схемы
,
11
)(
1
1вх
Cp
CpR
Cp
RpZ
+
=+=
2ос
)( RpZ
=
.
Рис. 3.8. ЛАЧХ и ЛФЧХ (а), переходные характеристика (б),
реального дифференцирующего звена и его реализация
на операционном усилителе (в)
G(
ω
)
+20дБ/дек
0
T
1
lg
lg
ω
G
0
π
2
ϕ(ω)
π
4
lg
ω
0
4
π
−
2
π
−
а
R2
R1 C
в
h(t)
T
k
0 t
б

Передаточная функция
11
1
)(
1
2
1
2
+
⋅
=
+
⋅−=
+
−=
Tp
pk
CpR
CpR
Cp
CpR
R
pW
,
где
CRk
2
= , CRT
1
= .
3.2.2. Звенья второго порядка.
В общем случае звено второго порядка описывается уравнением
)()(
)()(
2
2
2
1
tkxty
dt
tdy
T
d
t
tyd
T =++
,
или в операторной форме записи
).()()1(
2
22
1
pkXpYpTpT =++
Отсюда определяем передаточную функцию:
.
1
)(
2
22
1
++
=
pTpT
k
pW
(3.1)
В зависимости от характера полюсов передаточной функции (3.1)
(корней уравнения
01
2
22
1
=++ pTpT ) различают апериодическое
звено второго порядка, колебательное и консервативное звенья.
3.2.2.1. Апериодическое звено второго порядка
Это звено имеет место при отрицательных вещественных полю-
сах передаточной функции (3.1), которую в этом случае можно пред-
ставить в виде:
()()
11
1
)(
43
2
22
1
++
=
++
=
pTpT
k
pTpT
k
pW
, (3.2)
где эквивалентные постоянные времени
43
, TT рассчитываются по
соотношению
2
1
2
22
4,3
42
T
TT
T −±=
. (3.3)
Анализируя выражение передаточной функции (3.2), можно сде-
лать вывод о том, что апериодическое звено второго порядка состоит
из двух инерционных (апериодических) звеньев с эквивалентными
постоянными времени
43
, TT , поэтому логарифмические частотные
характеристики этих инерционных звеньев складываются.
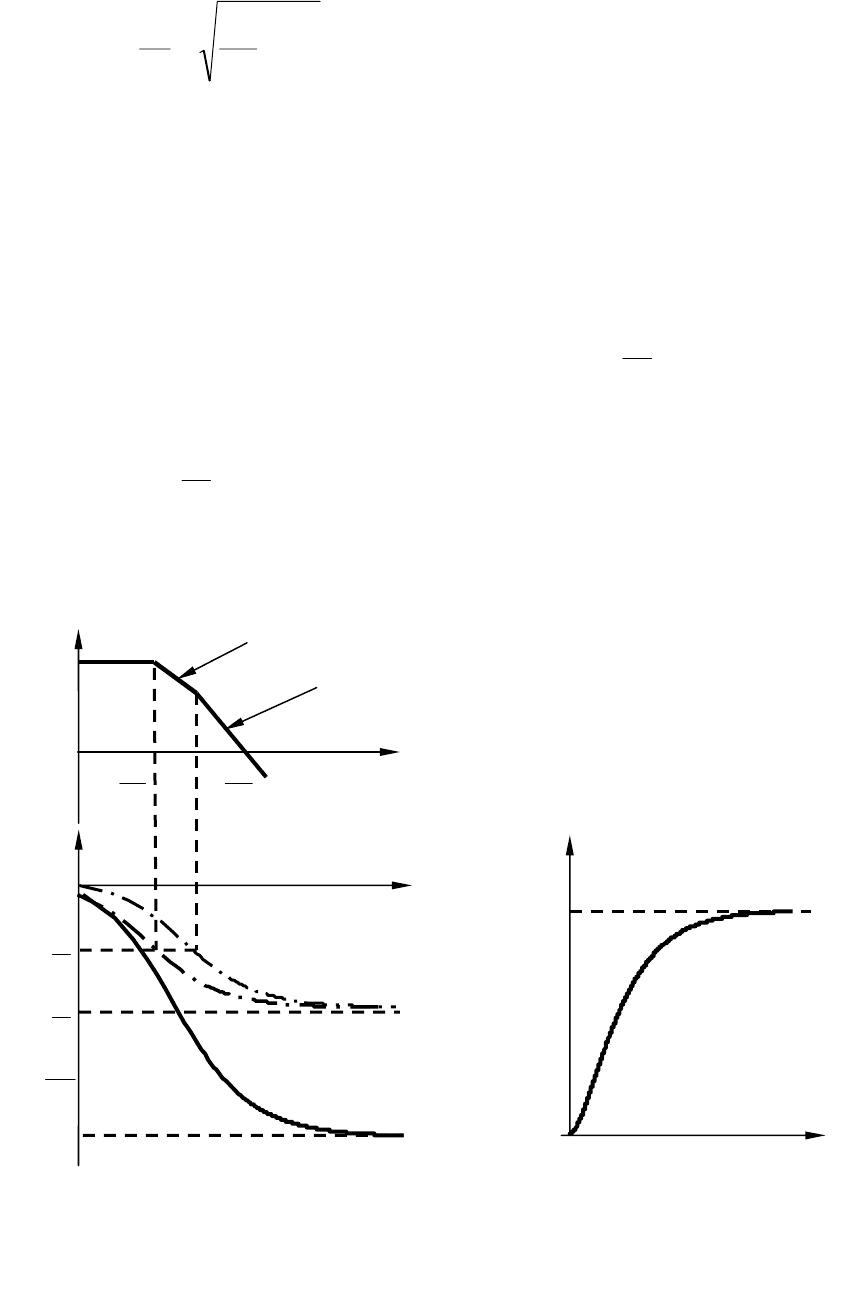
На рис. 3.9, а показаны ЛАЧХ и ЛФЧХ апериодического звена
второго порядка. До частотны сопряжения
3
c1
1
T
=ω
ЛАЧХ горизон-
тальна на уровне
kG lg20
0
=
, после этой частоты до частоты сопря-
жения
3
c2
1
T
=ω
имеет наклон –20 дБ/дек, а после
c2
ω проходит с
наклоном –40 дБ/дек. ЛФЧХ асимптотически приближается к значе-
нию
π− .
G(
ω
) -20дБ/дек
G
0
-40дБ/дек
0
3
1
lg
T
4
1
lg
T
lg
ω
ϕ(ω)
0
lg
ω
4
π
−
2
π
−
4
3
π
−
π
−
а
Рис. 3.9. ЛАЧХ и ЛФЧХ (а), переходная характеристика (б),
апериодического звена второго порядка
h(t)
k
0 t
б

По формуле (2.14) получим расчетное выражение для переходной
функции апериодического звена второго порядка. Для него
k
B
p
B ==)( ,
(
)
(
)
11)(
43
+
+
= pTpTpA
,
4343
2)( TTpTTpA ++
=
′
,
3
1
1
T
p −=
,
4
2
1
T
p −=
, тогда
.1
)(
)(
)(
)(
)0(
)0(
)(
4
3
21
34
4
34
3
22
2
11
1
−
−
−
+=
=
′
+
′
+=
−
−
T
t
T
t
tptp
e
TT
T
e
TT
T
k
pAp
epB
pAp
epB
A
B
th
Переходная характеристика звена показана на рис. 3.9, б, ее ха-
рактерная особенность – наличие точки перегиба вследствие сумми-
рования двух экспоненциальных составляющих.
3.2.2.2. Ко л е б а т е л ь н о е звено
Это звено получается при комплексных сопряженных полюсах
передаточной функции (3.1). Передаточную функцию звена удобнее
записывать в виде:
12
)(
22
+ξ+
=
TppT
k
pW
,
где
1
TT = , а параметр
1
2
2T
T
=ξ
называется коэффициентом демп-
фирования. Для колебательного звена
10
<
ξ
<
. Можно также отме-
тить, что при
1≥ξ полюсы передаточной функции (3.1) становятся
вещественными и звено будет апериодическим второго порядка.
Получим формулы для частотных характеристик колебательного
звена:
(
)
(
)
222
2
22
22
22
41
21
21
)(
TT
TjTk
TjT
k
jW
ωξ+ω−
ξω−ω−
=
ξω+ω−
=ω
,

(
)
(
)
222
2
22222
2
22
22
41
2
)( ,
41
1
)(
TT
T
kQ
TT
T
kP
ωξ+ω−
ξω
−=ω
ωξ+ω−
ω−
=ω
,
(
)
222
2
22
41
)()(
TT
k
jWA
ωξ+ω−
=ω=ω
,
(
)
222
2
22
41lg20lg20)( TTkG ωξ+ω−−=ω ,
22
1
2
arctg
)(
)(
arctg)(
T
T
P
Q
ω−
ξ
ω
−=
ω
ω
=ωϕ .
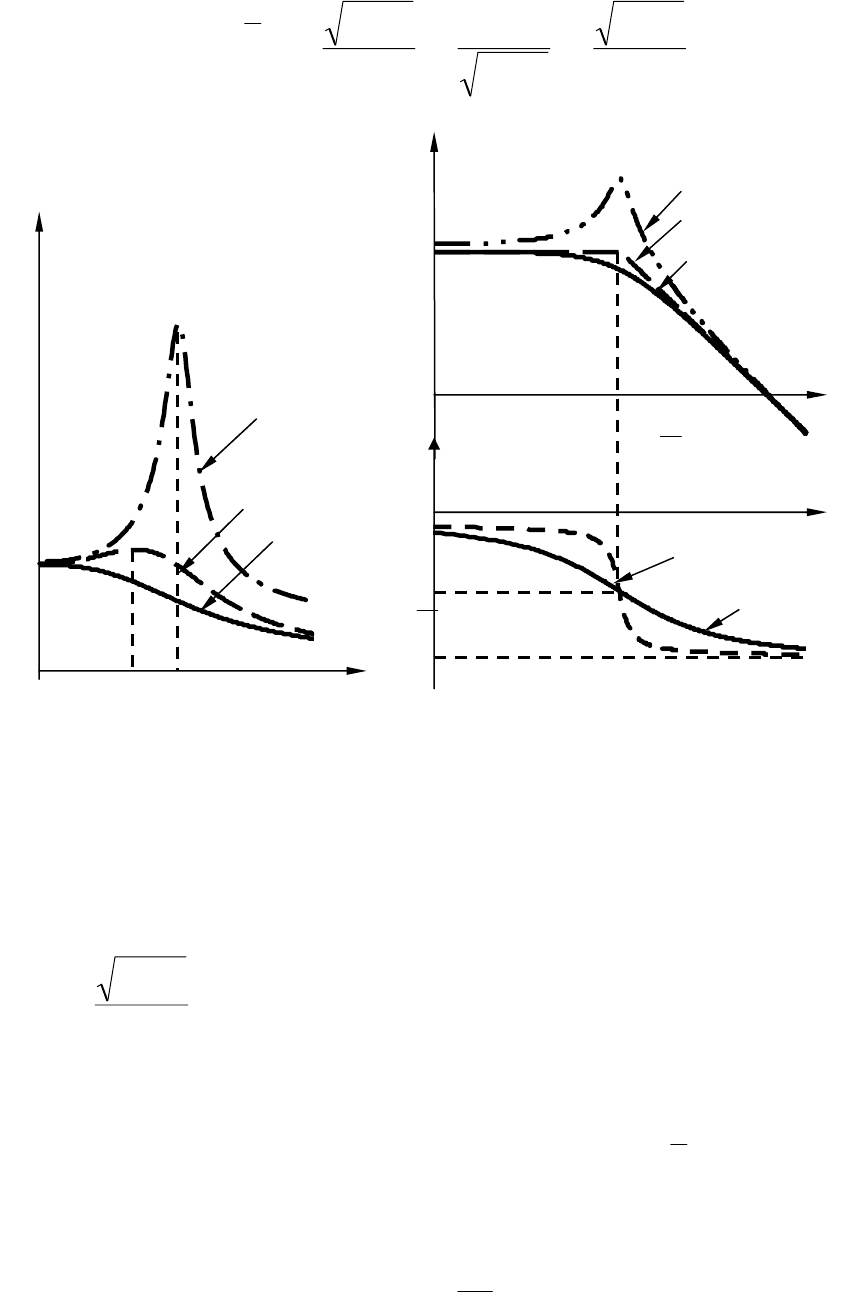
Частотные характеристики колебательного звена приведены на
рис. 3.10. Они существенно зависят от величины коэффициента
демпфирования
ξ
. При 707,01 >
ξ
> АЧХ )(
ω
A
(рис. 3.10, а) моно-
тонно уменьшается с увеличением частоты. При
707,0
<
ξ
на ней по-
является «горб», который увеличивается по мере уменьшения
ξ
. На
ЛАЧХ (рис.3.10, б) «горб» проявляется при
5,0
<
ξ
, при больших
значениях коэффициента демпфирования ЛАЧХ приближается к ее
асимптотическому варианту (имеет нулевой наклон до частоты со-
пряжения
T
1
c
=ω и наклон – 40дБ/дек после этой частоты). Вели-
чина «горба» на частоте
2
к
21
1
ξω
−=
T
может быть оценена по со-
отношению [6]:
ξ
≈
ξ−ξ
=
2
1
lg20
12
1
lg20
2
H .
Переходная функция колебательного звена может быть получена
по формуле (2.14) при комплексных сопряженных полюсах
T
p
1
2
2,1
−ξ±ξ−
=
(при 1
<
ξ
выражение 1
2
−ξ становится меньше
нуля):
ξ−
ξ−
ξ
+
ξ−
−=
ξ
−
t
T
t
T
ekth
T
2
2
2
1
sin
1
1
cos1)(
. (3.4)
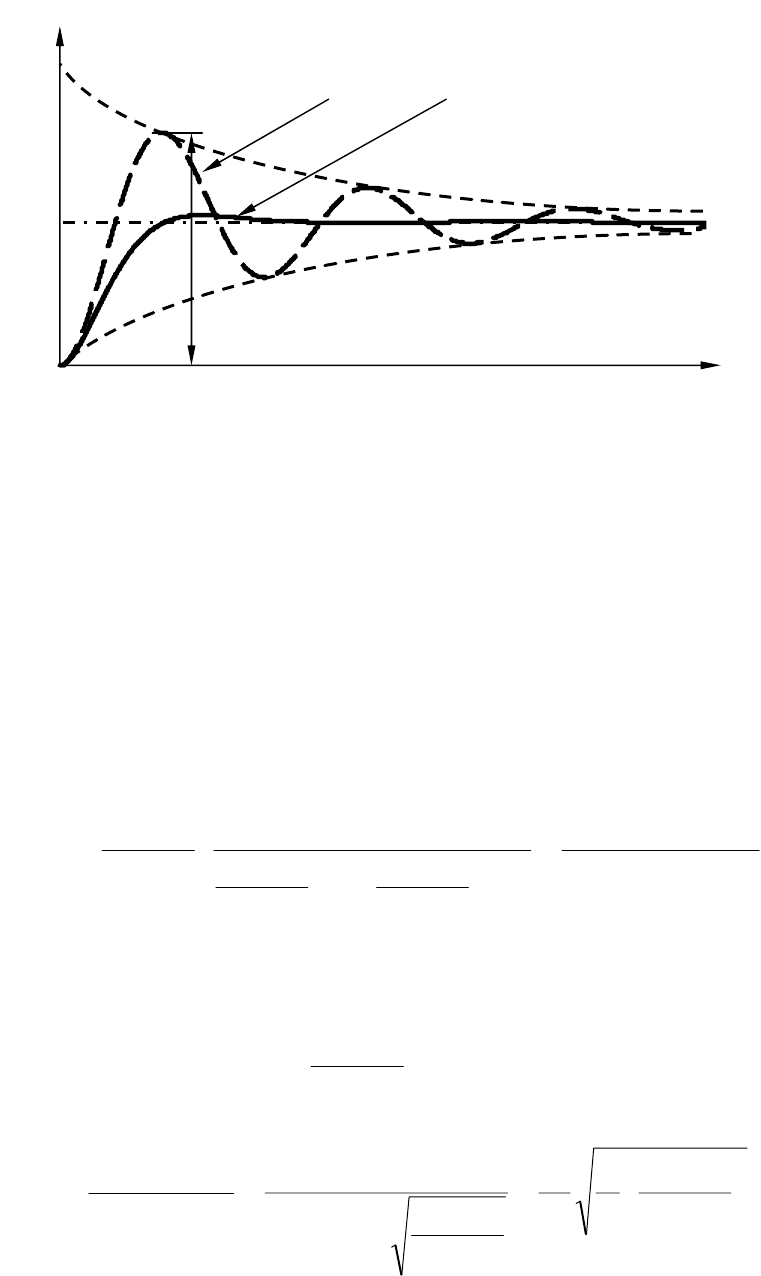
На рис. 3.11 по казаны переходные характеристики колебательно-
го звена, рассчитанные по выражению (3.4) для различных значений
коэффициента демпфирования
ξ
. Частота собственных колебаний
переходной характеристики оценивается по выражению
T
2
к
1
ξ
ω
−
=
и равна мнимой части полюсов
2,1
p . Ее можно также
определить и по АЧХ (см. рис. 3.10, а, частоты
к1
ω
и
к2
ω
, соответ-
ствующие максимальным значениям на АЧХ). Огибающая (см. пунк-
тир на рис. 3.10) определяется формулой
t
T
keth
ξ
−
=)(
0
. Время пере-
ходного процесса на практике оценивается соотношением
ξ
T
t
пп
3
≈
.
A(ω)
ξ → 0
ξ < 0,707
ξ > 0,707
k
0
ω
к1
ω
к2
ω
а
G(
ω
)
ξ < 0,5
- 40 дБ/дек
G
0
ξ > 0,5
lg
ω
0
T
1
lg
ϕ(ω) lgω
ξ < 0,5
2
π
− ξ > 0,5
π
−
б
Рис.3.10. Частотные характеристики колебательного звена
Примером звена второго порядка может служить колебательный
контур (см. схему на рис. 2.6 и вывод передаточной функции в при-
мере 2.5).
Пример 3.2.
Определить, при каком соотношении параметров элементов схе-
мы колебательный контур (см. рис. 2.6) является колебательным зве-
ном.
Запишем полученную в примере 2.5 передаточную функцию с
использованием коэффициента демпфирования:
.
12
1
1
)(
22
21
21
2
21
2
21
2
+ξ+
=
+
+
+
+
+
=
TppT
k
p
RR
CRR
p
RR
LCR
RR
R
pW
Отсюда выразим коэффициент демпфирования:
;2
21
21
T
RR
CRR
ξ
=
+
()
()
+
=
+
+
=
+
=ξ
21
21
21
2
21
21
21
21
2
2
2 RR
R
L
CR
RR
LCR
RR
CRR
RRT
CRR
.
Звено будет колебательным, если
1
<
ξ
, т.е.
h(t)
ξ = 0,15 ξ = 0,7
k
h
max
0 t
Рис. 3.11. Переходные характеристики колебательного звена

2
21
2
1
<
+ RR
R
L
C
R
.
В противном случае, т.е. при
2
21
2
1
≥
+ RR
R
L
C
R
контур будет являться апериодическим звеном второго порядка.
Следует обратить внимание на то, что лишь с позиций математи-
ческого описания схему можно представить как последовательное
соединение двух апериодических звеньев первого порядка. Расчле-
нить же принципиальную схему на два участка, каждый из которых
был бы соответствующим апериодическим звеном первого порядка,
невозможно.
Пример 3.3.
Вывести передаточную функцию и определить ее параметры для
устройства, схема которого приведена на рис 3.12, а.
Устройство выполнено на операционных усилителях, реализую-
щих инерционное, интегрирующее и пропорциональное звенья (см.
разделы 3.2.1.1, 3.2.1.2, 3.2.1.4).
На выходе усилителя У1 происходит
преобразование и суммирование напряжений по каждому из его вхо-
дов. Его передаточные функции относительно входного напряжения
U
вх
и напряжения обратной связи U
oc
представляются выражения-
ми
() ()
1
)( ,
1
)(
132
3
2
131
3
1
+
−=
+
−=
pCRR
R
pW
pCRR
R
pW
.
Полученный сигнал проходит через последовательно включенное
интегрирующее звено на усилителе У2, с передаточной функцией
pCR
pW
24
3
1
)( −=
.
Выход усилителя У2 образует выход устройства и сигнал с него
через усилитель У3 с передаточной функцией
5
6
4
)(
R
R
pW −= поступа-
ет на второй вход усилителя У1.
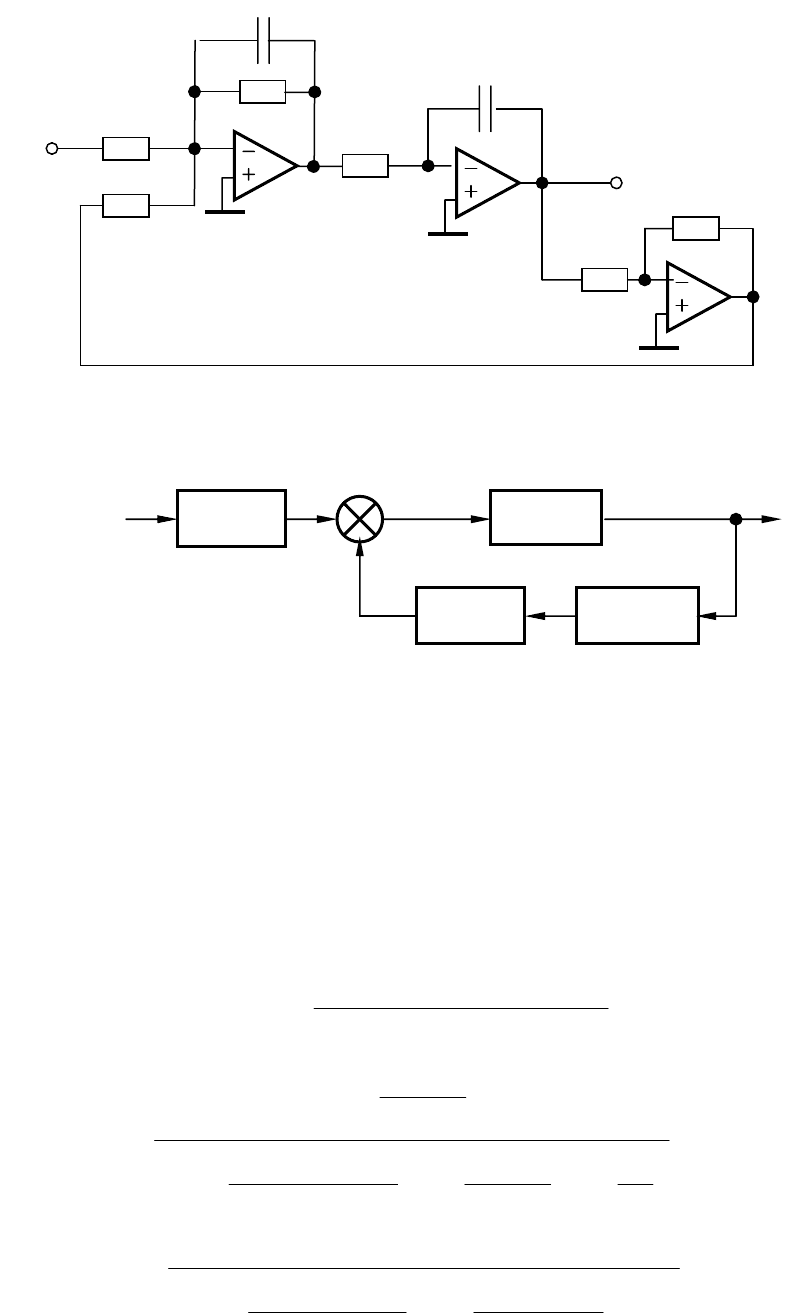
На рис. 3.12, б приведена структурная схема, соответствующая
устройству, изображенному на рис.3.12, а. Эквивалентная переда-
точная функция участка схемы, охваченного обратной связью, рас-
считывается по выражению
:
=
⋅⋅−
=
)()()(1
)(
)(
431
3
экв
pWpWpW
pW
pW
()
=
−⋅
−⋅
+
−−
−
=
5
6
24132
3
24
1
1
1
1
R
R
pCRpCRR
R
pCR
(
)
.
1
1
63
2542
2
6
21542
63
1352
++
+
=
p
RR
CRRR
p
R
CCRRR
RR
pCRRR
C1
R3
C2
U
вх
R1 У1 R4
R2 У2
U
вых
R6
R5
У3
а
Рис. 3.12. Устройство на операционных усилителях (а) и его
ст
ру
кт
ур
ная схема
(
б
)
б
)(
1
pW
)(
3
pW
)(
1
pW )(
oc
pW
Up
вх
()
Up
вы
х
()
Up
oc
()
