Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

т. е. в этом случае выполняется соотношение (2.23):

ко = А ехр (— Я/ЛГ).

Разделив приближенное выражение (2.23) на исходное (более точное)

выражение к

= А

ехр (—EJRT), получим:

к/ко = (Г/Г)" ехр (1 -- f /Т) п. (2.28)

Если среднюю температуру Г выбрать как среднее геометрическое

и Г

, т. е.

Т = (TIT

то при п = 1 и = 2 для отношения (2.28) будем иметь при Т =

значение 0,93 и при Т = Т

— 0,95; т. е. в этом случае приближенная

формула (2.23) отличается от более точной

при Г > Т максимум на 5% и при Т ^

Т —

на 7%. При п = 2 ошибка больше и состав-

ляет соответственно 10—13% при TJT

= 2

и 12—17% при п=1 и TJ1\ = 3.

Таким образом, в не очень большом тем-

пературном интервале при обычных ошибках

опыта значения константы скорости, вычис-

ляемые по простой формуле Аррениуса (2.23)

и формуле, в которой учитывается зависи-

мость предэкспоненциального множителя от

температуры, могут оказаться неразличи-

мыми.

Зависимость скорости химической реак-

ции от температуры является хорошо из-

вестным экспериментальным фактом. Обыч-

но скорость реакции растет с повышением

температуры. В качестве примера на рис. 2

показана зависимость констант скоростей

прямой и обратной реакций Н

+ J

^ 2НJ

от температуры в интервале 283—508°С (по

данным Боденштейна [513]). В координатах 1 gk — 1 IT опытные точки

ложатся на прямые, что свидетельствует о соблюдении закона Аррениуса

для обеих реакций. Из наклона прямых

^ * (2.29)

i,4 4,6 1

<ЦТ-10

Рис. 2. Температурная зави-

симость констант скорости ре-

акции образования к (1) и раз-

ложения к' (2) иодистого водо-

рода [513]

d (1 /Г)

Боденштейн вычислил следующие значения энергии активации: Е (пря-

мая реакция) = 40 ккал/молъ и Е' (обратная реакция) = 44 ккал/молъ

Наглядное представление о температурном ходе реакции дает ее тем-

пературный коэффициент г]

, определяемый отношением констант ско-

рости реакции при двух температурах, отличающихся одна от другой на

некоторую небольшую величину 2ДТ (например, АТ = 5°)

Г]

= k

T+AT

. (2.30)

Вычисляя температурный коэффициент по формуле (2.23), получим:

2Д7'

—

ехр

R г2

ехр

Е 2АТ

Я Т*

(2.31)

В дальнейшем в случае всех энергетических величин, относящихся к молярным

количествам, вместо кал/молъ или ккал/молъ будем писать кал или соответ-

ственно ккал.

Как видно из этой формулы, температурный коэффициент простой реакции

при Е > 0 всегда должен быть больше единицы и должен уменьшаться

с увеличением температуры, стремясь к единице при Т ->- оо. Так, зна-

чения температурного коэффициента реакции Н

+ J

— 2HJ при 600,

650 и 700° К (вычисленные для

Т — 5°) равны соответственно 1,78;

1,65 и 1,51.

При энергии активации, равной нулю, температурный коэффициент

реакции, скорость которой выражается законом Аррениуса (что не всегда

имеет место), очевидно, равен единице.

В общем случае при энергии активации экзотермического направления

реакции Е ;> 0, энергия активации обратной (эндотермической) реакции

jЕ" = # + где Q — тепловой эффект реакции. В случае Е = 0 энергия

активации Е

равна эндотермике реакции, E

= Q. Энергию активации

экзотермического направления реакции иногда называют истинной энер-

гией активации.

Как увидим ниже, элементарная реакция (при учете активации мо-

лекул, т. е. экспоненциального члена в формуле Аррениуса), Как прави-

ло, осуществляется далеко не при каждом соударении.

Отношение предэкспоненциального множителя в формуле Аррениуса

к частоте столкновений (равной числу столкновений в 1 см

в 1 сек, делен-

ному на произведение концентраций сталкивающихся частиц) называется

стерическим.множителем (Р). Как правило, Р является величиной, мень-

шей единицы, и лишь в редких случаях имеет значение, близкое к еди-

нице

Кроме реакций, характеризующихся температурным коэффициентом

т]т = 1, известны реакции, для которых эффективный температурный

коэффициент оказывается меньше единицы, что формально отвечает Е <

<С 0. К таким реакциям в основном относятся реакции рекомбинации, ко-

торые будут рассмотрены в главе VI.

Согласно термодинамике, константа равновесия может быть представ-

лена в виде:

= ехр (ASpR) ехр (- Q°

IRT) (2.32)

или соответственно в виде:

= ехр (AS

JR) ехр (- Qj/ЛГ), (2.33)

где AS

— изменение энтропии в результате реакции; 0% и Ql — теплоты

реакции соответственно при постоянном давлении и постоянном объеме

(при Т = 0°К), причем

Q°

— Q°

=AvRT и —

AS°

= AvR In RT (2.34)

(Av — изменение числа молей).

Из (2.33) и выражения К

= k/k' следует, что если теплота реакции

связана с разностью энергий активации прямой и обратной реакций

£Г0 __ £0

то между предэкспоненциальными множителями А и А' в аррениусов-

ском выражении констант скорости (2.23) и величиной AS

имеет место

соотношение:

RLN(A/A') = AS°. (2.35)

Это соотношение часто используется для нахождения величины А/А\

поскольку энтропия газа может быть выражена через суммы состояний,

вычисляемые из спектроскопических и других данных.

Здесь мы рассматриваем закон Аррениуса как выражающий установ-

ленную на опыте зависимость константы скорости реакции от температу-

ры в некотором температурном интервале. Между тем, ряд соображений,

в основном базирующихся на статистической теории, указывают на при-

ближенный характер закона Аррениуса (см., например, [1041]). Этот вопрос

подробно будет рассмотрен в главах III, V и VII.

§ 3. СЛОЖНЫЕ РЕАКЦИИ

Мы различаем простые и сложные химические реакции.

Простыми реакциями мы назвали такие реакции, стехиометрический

порядок которых совпадает с их истинным порядком и скорость которых

выражается законом действующих масс.

Вместе с тем любая простая химическая реакция (т. е. реакция, не

осложненная вторичными процессами) за редкими исключениями пред-

ставляет собой многостадийный процесс. В случае реакций, идущих с энер-

гией активации, какими является подавляющее большинство химических

реакций, эта многостадийность обусловлена тем, что кроме химического

превращения активных молекул в механизм этих реакций входят физиче-

ские процессы активации и дезактивации. В случае реакций присоедине-

ния и рекомбинации свободных радикалов, не требующих предваритель-

ной активации, механизм реакции слагается из процессов образования,

распада и стабилизации квазимолекул.

Как уже отмечалось ранее, совпадение наблюдаемого порядка реак-

ции с.ее стехиометрическим порядком является необходимым, хотя и не-

достаточным критерием того, что данная реакция представляет собой про-

стую реакцию. Всякое отклонение наблюдаемого порядка реакции от

стехиометрического нужно рассматривать как бесспорный признак того,

что данная реакция не принадлежит к числу простых реакций, а является

сложной реакцией. С точки зрения ее внутреннего механизма сложная ре-

акция представляет собой совокупность простых химических реакций

мл и элементарных процессов, следующих один за другим или совершаю-

щихся параллельно.

Реакции с последовательными стадиями

Для кинетики многих сложных реакций характерно наличие двух или

нескольких химических стадий, следующих одна за другой. Такие реак-

ции можно назвать реакциями с последовательными стадиями. Эти реак-

ции, очевидно, представляют собой такие двух- или многостадийные реак-

ции, в первой стадии которых образуется вещество, способное к дальней-

шему химическому превращению, осуществляющемуся в последующие

стадии реакции. Такие вещества называются промежуточными веществами,

В качестве одного из примеров последовательных реакций укажем реак-

цию между парами натрия и парами сулемы HgCl

, наблюдающуюся в так

называемых высокоразреженных пламенах (см. § 6), т. е. реакцию

2Na + HgCl

=2NaCl + Hg.

Детальное исследование этой реакции (и аналогичных ей реакций) при-

водит к заключению, что механизм ее представляет совокупность двух по-

следовательных стадий:

Na + HgCl

=NaCl + HgCl,

HgCl + Na=NaCl + Hg.

Отметим, что двухстадийыость этих реакций наглядно проявляется в су-

ществовании двух зон реакции: зоны максимального выхода продукта

реакции и зоны максимального выхода света (см. § 6). Промежуточным

веществом в рассмотренной реакции является одновалентный радикал

HgCl.

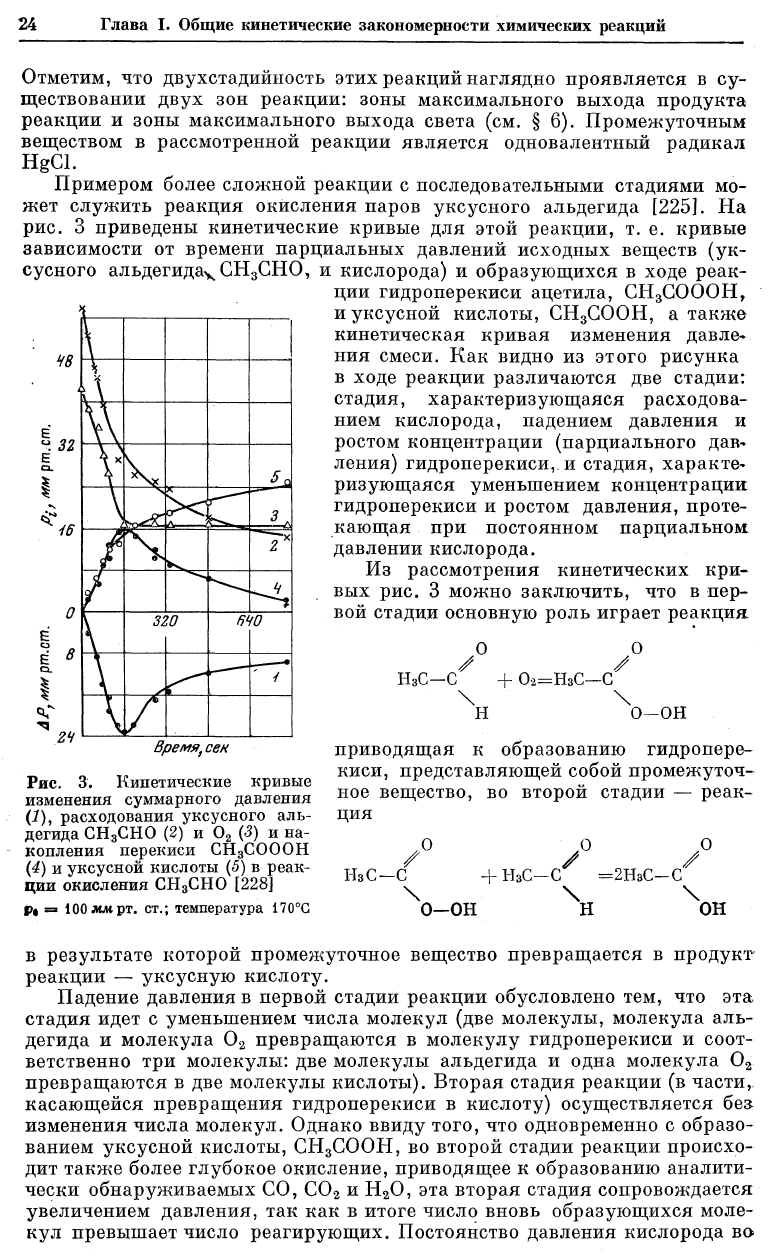
Примером более сложной реакции с последовательными стадиями мо-

жет служить реакция окисления паров уксусного альдегида [225]. На

рис. 3 приведены кинетические кривые для этой реакции, т. е. кривые

зависимости от времени парциальных давлений исходных веществ (ук-

сусного альдегида

СН

СНО, и кислорода) и образующихся в ходе реак-

ции гидроперекиси ацетила, СН

СОООН,

и уксусной кислоты, СН

СООН, а также

кинетическая кривая изменения давле-

ния смеси. Как видно из этого рисунка

в ходе реакции различаются две стадии:

стадия, характеризующаяся расходова-

нием кислорода, падением давления и

ростом концентрации (парциального дав-

ления) гидроперекиси, и стадия, характе-

ризующаяся уменьшением концентрации

гидроперекиси и ростом давления, проте-

кающая при постоянном парциальном,

давлении кислорода.

Из рассмотрения кинетических кри-

вых рис. 3 можно заключить, что в пер-

вой стадии основную роль играет реакция

о.

У >

ч \

НзС-С + 0-2=НзС—С

о—он

Время,

се и

Рис. 3. Кинетические кривые

изменения суммарного давления

(i), расходования уксусного аль-

дегида СН

СНО (2) и 0

(3) и на-

копления перекиси СН

СОООН

(4) и уксусной кислоты (5) в реак-

ции окисления СН

СНО [228]

Pi = ЮОлшрт. ст.; температура 170°С

приводящая к образованию гидропере-

киси, представляющей собой промежуточ-

ное вещество, во второй стадии — реак-

ция

/О О О

/ / /

Из

С —С

+ НзС-С =2НзС—С

\ \ \

о-он н он

в результате которой промежуточное вещество превращается в продукт-

реакции — уксусную кислоту.

Падение давления в первой стадии реакции обусловлено тем, что эта

стадия идет с уменьшением числа молекул (две молекулы, молекула аль-

дегида и молекула 0

превращаются в молекулу гидроперекиси и соот-

ветственно три молекулы: две молекулы альдегида и одна молекула 0

превращаются в две молекулы кислоты). Вторая стадия реакции (в части,

касающейся превращения гидроперекиси в кислоту) осуществляется без

изменения числа молекул. Однако ввиду того, что одновременно с образо-

ванием уксусной кислоты, СН3СООН, во второй стадии реакции происхо-

дит также более глубокое окисление, приводящее к образованию аналити-

чески обнаруживаемых СО, С0

и Н

0, эта вторая стадия сопровождается

увеличением давления, так как в итоге число вновь образующихся моле-

кул превышает число реагирующих. Постоянство давления кислорода во

второй стадии реакции свидетельствует о том, что превращение гидро-

перекиси в уксусную кислоту (и продукты глубокого окисления) в этой

стадии реакции происходит без участия свободного кислорода.

Заметим, что написанная выше схема реакции окисления уксусного

альдегида в кислоту формально соответствует одной из схем окисления*

фигурирующих в переписной теории окисления Баха — Энглера (см. [384]).

Согласно этой теории, первая стадия окислительной реакции заключается

в образовании «мольоксида» М0

, представляющего собой продукт пря-

мого присоединения молекулы кислорода к молекуле горючего:

м + О

=М

«Мольоксид» в результате изомеризации превращается в обычную пере-

кись, например,

НзС—С + 0

= НзС—СН О—Н

С—С

\ \ / \

Н О - о—он

Вторая стадия окислительной реакции, по Энглеру [384], следует схеме:

М0

4* М==2МО,

отвечающей в нашем примере реакции

НзС-С + НзС—С = 2Н

С-С

\ \ \

О—ОН Н ОН

Что касается действительного механизма реакции окисления уксус-

ного альдегида, то подобно реакциям окисления всех вообще органиче-

ских веществ она протекает по сложному механизму, в котором главную

роль играют свободные радикалы (радикальный механизм) (см. [890

891, 1222, 1263]).

Из сложных реакций с ярко выраженной стадийностью укажем еще

реакцию окисления водорода, проводимую в условиях быстрой струи.

Согласно данным анализа, продуктами этой реакции являются вода и пе-

рекись водорода, причем содержание последней в продуктах реакции резко

падает с увеличением времени пребывания смеси в зоне реакции (т), как

это видно, в частности, из рис. 4 [173]. При достаточно малых временах

контакта содержание Н

достигает 85% от общего количества продук-

тов, из чего можно заключить, что первичным продуктом окисления во-

дорода в условиях рассматриваемых опытов является перекись водорода,

превращающаяся в воду в последующие стадии реакции. Механизм окис-

ления водорода будет рассмотрен ниже (§ 43).

Для выяснения кинетических особенностей реакций с последователь-

ными стадиями рассмотрим общий случай последовательной реакции, в ко-

торой вещество А превращается в В, которое в свою очередь превращается

в продукт реакции С,

А —»В С.

Детали кинетики реакций этого типа, естественно, зависят от механизма

каждой из стадий. Однако, имея в виду получение общей кинетической

характеристики реакций, протекающих через последовательные стадии,.

можем ограничиться рассмотрением простейшего случая, когда каждая из

двух стадий реакции представляет собой мономолекулярный про-

цесс. Хороший пример последовательных процессов, каждый из которых

подчиняется мономолекулярному закону, представляют процессы

радиоактивного превращения, наблюдающиеся в радиоактивных

рядах.

Обозначая константы скорости мономолекулярного превращения А

в В и В в С соответственно через к

и /с

, напишем уравнения реакций в

виде:

d[ А]

d[ В]

d[ С]

= [А],

= A:i [А] — [В], (3.1)

/£2

[В].

Вводя, далее, обозначения х= [А]/[А]

, у = [В]/[А]

и z = [С]/[А]

, где

|А]

— начальная концентрация исходного вещества А, эти уравнения

перепишем в следующем более простом виде:

dx dy dz

-"1ь=

klX

> ИТ =

klX

- ~Jt = (

Решая эти уравнения, получим:

х = ехр (— kit),

къ — кг

ехр klt

ехр

3,3

)

ехр

ы)

+ "л^ЛГ

ехр

ы)

Изменение величин х, у и z во времени, рассчитанное по формулам (3.3)

показано на рис. 5 (для к

\к

— 0,1; 1 и 10). Нетрудно видеть, что равенст-

во нулю производной dyldt = 0 достигается при том же времени t, что и

равенство нулю d^zldt

. Это значит, что кривая у = у (t) имеет максимум

при том же t, при котором кривая z = z (t) имеет точку перегиба. Время

достижения максимума

Подставляя т в выражение для относительной концентрации промежуточ-

ного вещества В, получим

Из анализа этого выражения следует, что величина у

тах

, малая при ма-

лых значениях отношения kjk

, растет при увеличении этого отношения,

проходя через значение е"

при kjk

= 1 и сколь угодно приближаясь

к единице при больших к

/к

(см. также рис. 6). В этом, последнем случае

вследствие большой скорости первой стадии реакции (А ->- В) и малой ско-

рости второй стадии (В

—>•

С), обе стадии оказываются разделенными во

времени, и реакция протекает так, что сначала все или практически все

исходное вещество А превращается в промежуточное вещество В, после

чего последнее превращается в продукт реакции С.

Таким образом, скорость образования продукта реакции, характери-

зующая скорость суммарной реакции, в этом случае определяется ско-

ростью наиболее медленной второй стадии реакции (лимитирующая ста-

дия), так как к

. Лимитирующая роль наиболее медленной стадии

реакции проявляется также и в обратном случае, когда к

. Дейст-

вительно, на основании (3.3) имеем

w-2

= Ыу =

___

{1 — ехр [—

(к* -г-

t]} wi,

откуда при к

и достаточно большом fe

получается w

= щ. Следо-

вательно, и в этом случае скорость образования продукта реакции, т. е.

скорость суммарной реакции, определяется скоростью ее самой медлен-

ной стадии. Эта закономерность является общей для всех сложных реак-

ций, осуществляющихся в две или несколько последовательных стадий.

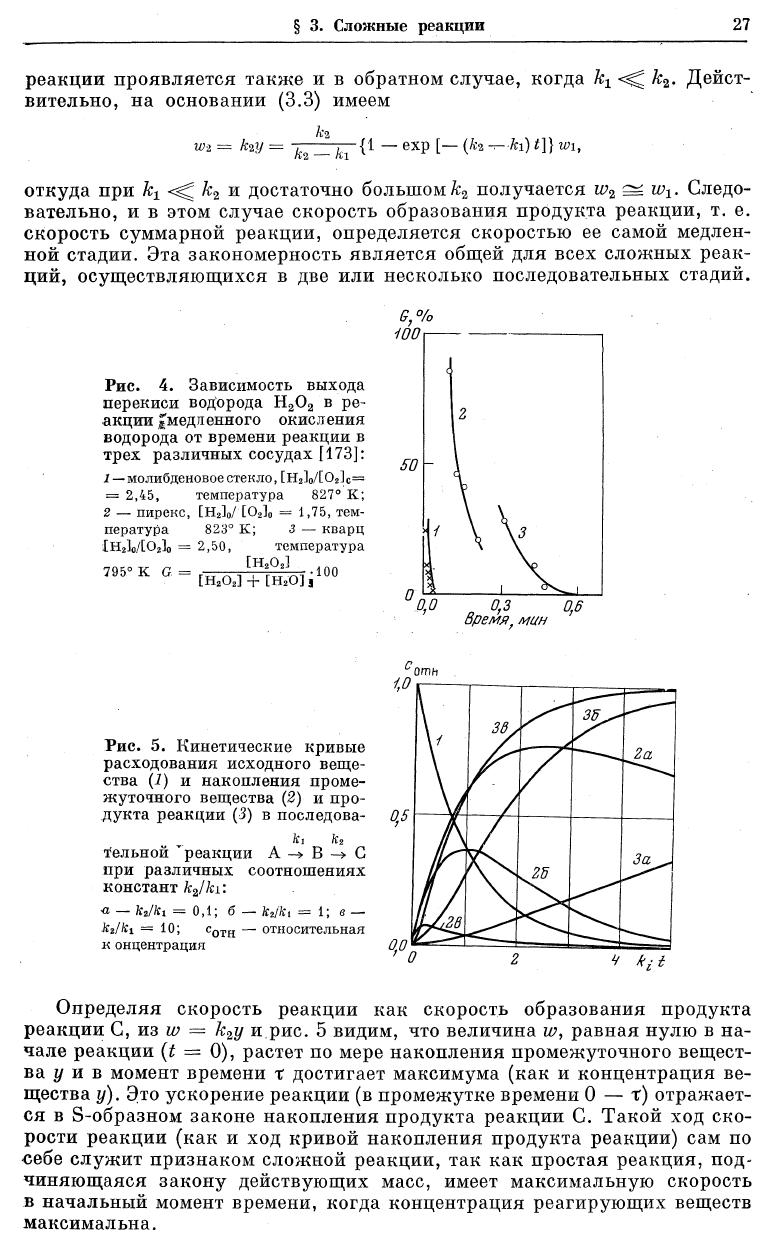
Рис. 4. Зависимость выхода

перекиси водЪрода Н

в ре-

акции £мед пенного окисления

водорода от времени реакции в

трех различных сосудах [173]:

1 —

молибденовое стекло, [Н

]о/[0

]с=

= 2,45, температура 827° К;

2 — пирекс, [Н

]

/ [О

]

= 1,75, тем-

пература 823° К; 3 — кварц

1Н

]о/[0

]о = 2,50, температура

[Н

795° К G =

[Н

] +

[Н

100

0,3 0.6

Время, мин

1,0

Рис. 5. Кинетические кривые

расходования исходного веще-

ства (i) и накопления проме-

жуточного вещества (2) и про-

дукта реакции (3) в последова-

ла к

тельной 'реакции А В G

при различных соотношениях

констант к

/кг.

— кг/кх

= 0,1; б

— kz/ki

1; в —

/ki ==10; с

отн

— относительная

к онцентрация

0,5

0.0*

36/

(L&ie

За^.

ч к j t

Определяя скорость реакции как скорость образования продукта

реакции С, из w = к

у и рис. 5 видим, что величина w, равная нулю в на-

чале реакции (t = 0), растет по мере накопления промежуточного вещест-

ва у и в момент времени х достигает максимума (как и концентрация ве-

щества у). Это ускорение реакции (в промежутке времени 0 — т) отражает-

ся в S-образном законе накопления продукта реакции С. Такой ход ско-

рости реакции (как и ход кривой накопления продукта реакции) сам по

себе служит признаком сложной реакции, так как простая реакция, под-

чиняющаяся закону действующих масс, имеет максимальную скорость

в начальный момент времени, когда концентрация реагирующих веществ

максимальна.

Нужно, однако, сказать, что при высокой химической активности

промежуточного вещества В (по сравнению с исходным веществом А) и,

следовательно, к

реакции с последовательными стадиями, как пра-

вило, протекают так, что максимум скорости реакции достигается на пер-

вых ее стадиях, т. е. практически в начальный момент времени t = 0.

Поэтому кинетика накопления продукта реакции с последовательными

стадиями в таких случаях отвечает монотонному уменьшению скорости

реакции от максимального значения (при £^0), т. е. отсутствию за-

метного перегиба на кривой z = z (t).

Метод квазистационарных концентраций

Второе слагаемое в выражении для скорости изменения концентрации

промежуточного вещества

чг =

kix

равное нулю в начале реакции и увеличивающееся со временем (так как

dyldt 0), в некоторый момент времени становится равным первому сла-

гаемому (уменьшающемуся по мере расходования исходного вещества А).

В этот момент времени (т) будем иметь dyldt = 0. Начиная с этого момента

при достаточно большом к

величина dyldt автоматически поддерживается

вблизи нуля. Поэтому можно считать, что при t т приближенно выпол-

няется равенство dyldt

0, вследствие чего одно из двух независимых диф-

ференциальных уравнений реакции (3.2) (третье уравнение, ввиду dxldt +

+ dyldt + dzldt = 0, не является независимым), а именно уравнение-

dyldt = к

х — к

у, мы можем заменить алгебраическим уравнением

х — к

у = 0, что приводит к существенному упрощению математической

задачи вычисления концентраций х, у и z. В рассматриваемом нами слу-

чае приближенные значения концентраций запишутся в виде:

—

ехр (— k\t)

у = (ki/k*) ехр (— kit), z = 1 — ехр (— kit). (3.5>

Сравнивая уравнения (3.5) и (3.3), легко видеть, что приближенные зна-

чения концентраций тем ближе к их точным значениям (3.3), чем больше

константа к

превышает к

. При k

^>k

те и другие совпадают.

Примененный здесь прием, широко используемый в химической кине-

тике, известен под названием метода квазистационарных концентраций.

Этот метод как метод приближенного решения кинетических уравнений

впервые был четко сформулирован Боденштейном [514], хотя в неявном

виде использовался и в более ранних работах других авторов. В дальней-

шем метод квазистационарных концентраций был обобщен Семеновым

[308] и распространен на случай, когда концентрации не всех (обычна

всех, кроме одного) активных центров являются стационарными. Обоб-

щенный метод Семенова иногда называют методом частичных стационарных

концентраций. Метод квазистационарных концентраций оказался осо-

бенно плодотворным при исследовании цепных реакций (см. главу XI).

Отметим также, что часто для реакций, идущих при участии несколь-

ких активных промежуточных веществ, принимаются обладающими ста-

ционарными концентрациями те активные частицы, концентрации кото-

рых малы по сравнению с концентрациями других активных частиц. Этот

вопрос на примере реакции брома с водородом был проанализирован в

работах [1487]. Авторы этих работ показывают, что неправильное в общем

случае заключение о связи стационарности с малостью концентраций в дан-

ной реакции практически всегда выполняется.

Детальное рассмотрение условий применимости метода стационарных

концентраций предпринималось рядом авторов для реакций различных

типов. См., например, работы [305, 365, 846, 958, 1327, 1407]. Были най-

дены случаи, когда условие стационарности заведомо не выполняется

(см., например, [992]).

Представляет интерес найти время установления стационарной концент-

рации (т). Рассмотрим с этой целью реакцию термического распада

озона. Механизм этой реакции слагается из следующих элементарных

процессов [474]:

0з + М^0 + 0

+ М (Ал, к-1)

0 + 0З = 20

(Ла),

где М — любая частица; к

, и к

— константы скорости соответствую-

щих процессов.

Промежуточным веществом здесь является атомарный кислород,

концентрация которого изменяется согласно уравнению:

к± [М]

] -

[А-1 [М]

] + ft

[Оз]] [О].

В начальный период реакции, когда концентрация озона еще мало отли-

чается от начальной концентрации [О

]

, интегрирование этого уравне-

ния дает:

[О] = [0]

стац

[1-ехр (--*/*)],

где [0]

стац

- ^ШНОзЬт ит- l/(^—i [М][0

] + Л

[О

]

Вычисление по последней формуле [135] дает т < 10сек (Т = 475° К).

К аналогичному результату приводит также расчет кинетики разложения

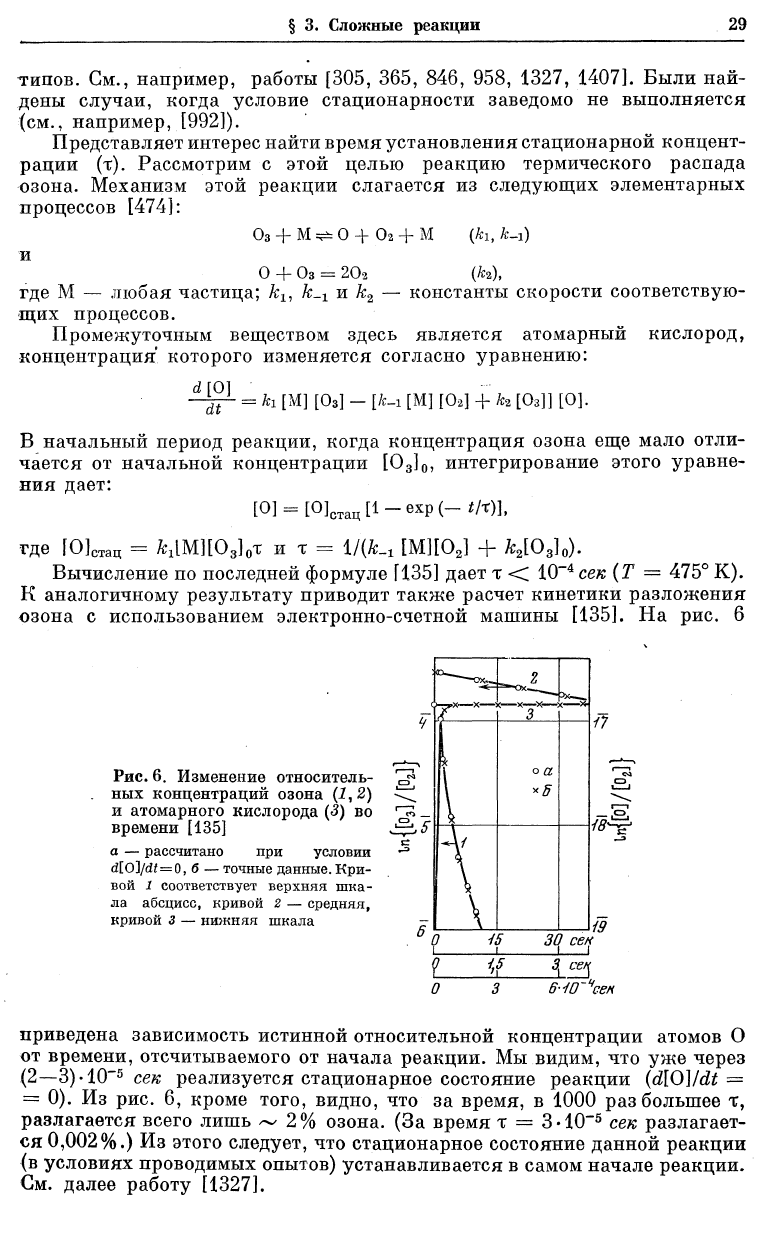
озона с использованием электронно-счетной машины [135]. На рис. 6

Рис. 6. Изменение относитель-

ных концентраций озона (1,2)

и атомарного кислорода (<?) во

времени [135]

а — рассчитано при условии

d[0]/df = 0, б — точные данные. Кри-

вой 1 соответствует верхняя шка-

ла абсцисс, кривой 2 — средняя,

кривой 3 — нижняя шкала

приведена зависимость истинной относительной концентрации атомов О

от времени, отсчитываемого от начала реакции. Мы видим, что уже через

(2—3)-10~

сек реализуется стационарное состояние реакции (d[0]/dt =

= 0). Из рис. 6, кроме того, видно, что за время, в 1000 раз большее т,

разлагается всего лишь ~ 2% озона. (За время т = 3-Ю"

сек разлагает-

ся 0,002%.) Из этого следует, что стационарное состояние данной реакции

(в условиях проводимых опытов) устанавливается в самом начале реакции.

См. далее работу [1327].

Параллельные реакции

Наряду с реакциями, протекающими через последовательные стадии,

необходимо различать также параллельные реакции. Простейшим типом

параллельных реакций являются такие реакции, когда одно и то же ис-

ходное вещество А способно реагировать двумя или более независимыми

путями, приводящими к одинаковым или различным продуктам реакции.

Параллельно идущие реакции могут быть моно- и бимолекулярными..

Рассмотрим сначала две параллельные мономолекулярные реакции.

Обозначив константы скорости этих реакций через к

и будем иметь:

d[ Ci] d[C

]

"У"-MA] и = /с

[А]. (3.6)

Разделив одно из уравнений на другое и интегрируя, найдем:

[Сз]/[Са] = Ап/Ага, (3.7>

откуда следует, что концентрации (выходы) продуктов параллельно иду-

щих реакций относятся как константы скорости этих реакций. Так как

вещества С

и С

образуются в результате расходования исходного вещест-

ва А, имеем:

d [A] d [Ci] d ГСа]

- -зг- = + "V = +ш =

[ (

Следовательно, константа скорости суммарной реакции при параллель-

ном течении двух (или нескольких) реакций равна сумме констант скоро-

сти этих реакций:

к = к\

-f- Аг

(^или к = ^ k

J .

В качестве примера параллельных мономолекулярных реакций мож-

но указать распад гидроперекиси RCH

OOH, который может идти двумя

путями — либо с отщеплением молекулы воды и образованием альдеги-

да, RCH

OOH — RCHO + Н

0, либо с разрывом связи О — О.

В последнем случае образуются свободный гидроксил и алкоксильный

радикал RCH

0, в дальнейшем превращающийся в спирт.

Простейший случай параллельной бимолекулярной реакции может

быть представлен схемой:

А + В

Отношение выходов продуктов в таких реакциях, так же как в рассмотрен-

ном выше примере мономолекулярных параллельных реакций, равно от-

ношению констант скорости параллельных реакций.

Так, для скоростей образования продуктов имеем:

d [Ci] d [С

]

= ki [А] [В] И -к_1

[А

][В], . (3.9)

откуда

£GiI/[Ga] = Ап/Ага. (3.9а)