Колпаков Б.А., Лебедев Б.О. Техническая физика. Часть 1 - Теплофизические основы судовой энергетики
Подождите немного. Документ загружается.

172
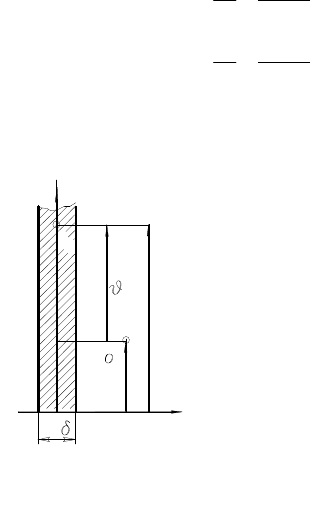
омывается с обеих сторон жидкостью или газом с температурой
c
t при
коэффициенте теплоотдачи
a
. Размеры пластины в направлении осей y
и z считаются неограниченными, а физические характеристики материа-
ла пластины - теплопроводность
l
, теплоёмкость с и плотность
r
- по-
стоянными.
Решение задачи представляется в виде:
),,(
),,(
BiFo f
tt
tt
BiFo f
tt
tt
c
cцц
c
cпп
2
1
=
-
-
=
=
-
-
=
q
q
q
q
(18.13)
где
цп
tt , - температуры на поверхности и в центральном сечении пла-
стины.
Отсутствие в формулах (18.13) линей-
ного симплекса объясняется тем, что в сред-
ней плоcкости и на поверхности пластины
температуры постоянны и изменяются толь-
ко в направлении оси x.
Теплота, передаваемая пластиной в ок-
ружающую среду за время
t
, равно измене-
нию внутренней энергии пластины за период
охлаждения.
Начальная внутренняя энергия пласти-
ны, отсчитанная от внутренней энергии при
температуре среды как от нуля, равна
rdqrd
ActtAcU
c
22
0
=-= )( (18.14)
Отношение теплоты, переданной за пе-
риод
t
, к начальной внутренней энергии пла-
стины определяется также безразмерными числами Био и Фурье:
),(/ FoBifUФ
30
=
t
(18.15)
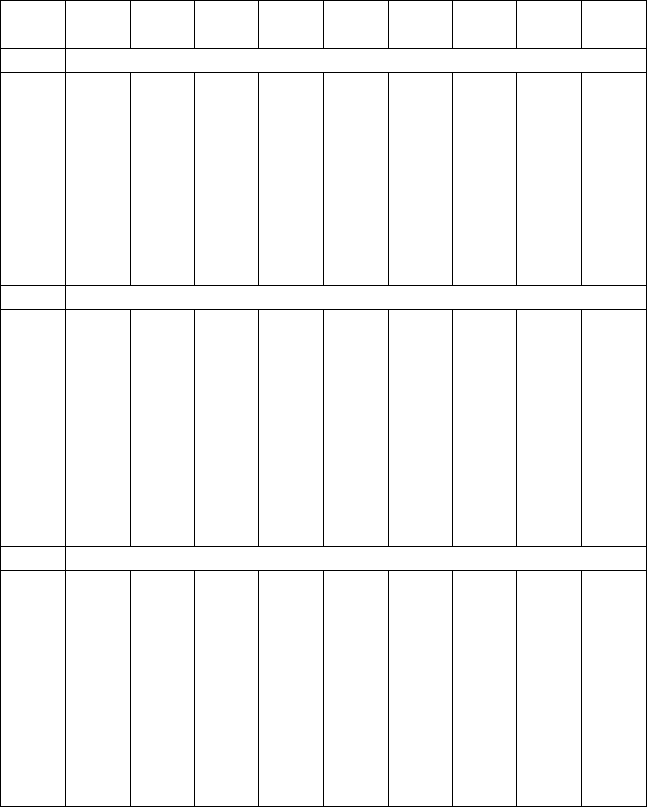
Конкретные решения уравнений (18.13,18.15) обычно представле-
ны в виде графиков или в табличной форме (cм. таблицу 18.1). При ре-
шении конкретной задачи вначале подсчитывают числовые значения
определяющих критериев, а затем, пользуясь таблицей, находят иско-
мые значения.
Рисунок 18.2
t
t
x
t
2
НГАВТ - Стр 201 из 239
Новосибирская Государственная Академия Водного Транспорта
173
Решения, аналогичные вышеизложенному, имеются для других
геометрических систем - цилиндрических тел, шаров и др.
Таблица 18.1 - Расчётные зависимости для пластины
Bi 0,00
1
0,01 0,1 0,5 1 4 10 20 50
Fo θ
п
/θ = f
1
(Fo,Bi)
0,05
0,1
0,5
1
2
5
10
20
50
1
1
1
1
0,99
0,98
0,96
1
0,99
0,99
0,98
0,95
0,90
0,82
0,61
1
0,97
0,92
0,83
0,62
0.37
0,14
0,01
1
0,87
0,70
0,46
0,13
0,02
0
1
0,78
0,54
0,31
0,03
0
1
0,98
0,56
0,25
0,06
0
1
0,97
0,46
0,16
0,02
0
1
0,96
0,41
0,13
0,01
0
1
0,95
0,39
0,12
0,01
0
Fo θ
ц
/θ = f
2
(Fo,Bi)
0,02
0,05
0,1
0,5
1
2
5
10
20
50
1
1
1
1
1
1
1
0,99
0,98
0,96
0,99
0,99
0,99
0,99
0,98
0,97
0,95
0,90
0,81
0,60
0,98
0,98
0,97
0,92
0,88
0,79
0,59
0,36
0,13
0,01
0,93
0,89
0,85
0,69
0,56
0,37
0,10
0,01
0
0,86
0,79
0,73
0,51
0,35
0,17
0,02
0
0,59
0,46
0,37
0,17
0,08
0,02
0
0,34
0,23
0,17
0,06
0,02
0
0,19
0,12
0,06
0,01
0
0,08
0,05
0,04
0,01
0
Fo Ф/θ = f
3
(Fo,Bi)
0,02
0,05
0,1
0,5
1
2
5
10
20
50
0,01
0,02
0,04
0,01
0,02
0,05
0,10
0,18
0,39
0,01
0,02
0,05
0,10
0,17
0,39
0,62
0,81
0,92
0,01
0,03
0,09
0,17
0,31
0,62
0,84
0,93
0,99
0,01
0,02
0,05
0,20
0,35
0,59
0,88
0,99
1
0,02
0,04
0,08
0,32
0,53
0,78
0,98
1
0,05
0,12
0,20
0,58
0,81
0,96
1
0,09
0,18
0,27
0,69
0,89
0,98
1
0,12
0,23
0,34
0,75
0,92
0,99
1
НГАВТ - Стр 202 из 239
Новосибирская Государственная Академия Водного Транспорта

174
18.4 Дифференциальные уравнения конвективного
теплообмена
Дифференциальные уравнения конвективного теплообмена учиты-
вают особенности гидродинамики потока и влияние различных факто-
ров на теплообмен между потоком и поверхностью твердого тела.
Гидродинамика потока описывается уравнением движения вязкой
жидкости (уравнением Навье-Стокса) и уравнением неразрывности
(сплошности) потока.
Уравнение движения учитывает влияние сил инерции (левая часть
уравнения), сил вязкостного трения (третье слагаемое в правой части),
сил статического давления (второе слагаемое в правой части) и гравита-
ционных сил (первое слагаемое в правой части). Оно определяет поле
скоростей во времени, а также в пространстве, и в проекции на ось х
имеет следующий вид:
).(
)
2
2
2
2
2
2
zyx
x
p
g
zyx
z
xx
x
z
x
y
x
x
›
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
¶w
w
¶
¶w
w
¶
¶w
¶t
¶w
r
+++-
=+++
›
(
(18.16)
где выделенное скобками в левой части выражение представляет собой
полную или субстанциальную (в пространственных и временных коор-
динатах) производную от скорости
tw
dD
x
/ . С учетом этого
x
x
dx
dp
g
d
D
wmr
t
w
r
2
Ñ+-= (18.16а)
Аналогично записываются уравнения в проекции на оси y и z:
y
y
dx
dp
d
D
wm
t
w
r
2
Ñ+-= (18.16б)
z
z
dx
dp
d
D
wm
t
w
r
2
Ñ+-= (18.16в)
В формулах (18.16):
r
- плотность вязкой жидкости,
zy›
www
,, -
проекции скорости на соответствующие оси x,y и z , p - давление,
m
-
коэффициент динамической вязкости.
НГАВТ - Стр 203 из 239
Новосибирская Государственная Академия Водного Транспорта

175
Уравнение сплошности выводится на основе закона сохранения
массы и говорит о том, что в любом сечении неразрывного потока жид-
кости или газа массовый расход имеет одно и то же значение:
0=+++
¶t
¶
¶
rw¶
¶
rw
¶
¶
rw¶
p
zyx
z
y
x
)(
)(
)(
(18.17)
В основу вывода дифференциального уравнения энергии для дви-
жущегося потока сжимаемой вязкой жидкости положен закон сохране-
ния энергии. Это уравнение определяет изменение температуры жидко-
сти во времени и в пространстве. В отличие от дифференциального
уравнения теплопроводности в уравнении энергии учитывается то об-
стоятельство, что в движущемся потоке температура изменяется не
только за счет нагревания или охлаждения, но и в связи с изменением
положения этой жидкости в пространстве. Этим объясняется появление
в правой части формулы (18.19) субстанциальной производной от ско-
рости:
zyx
z
t
y
t
x
tt
ta
w
¶
¶
w
¶
¶
w
¶
¶
¶t
¶
+++=Ñ
2
(18.19)
Дифференциальное уравнение, описывающее процесс теплообмена
на границе жидкости и стенки (16.3) , уже было применено ранее в п.
16.2.
18.5 Условия гидродинамического подобия
Для двух подобных систем, в которых протекают подобные про-
цессы, записываются уравнения движения
)
"
"
"
"
"
"
("
"
"
"
)"
"
"
"
"
"
"
"
"
("
"
"
"
),(
)(
2
2
2
2
2
2
2
2
2
2
2
2
zyx
x
p
g
zyx
zyx
x
p
g
zyx
xxx
z
x
y
x
x
xx
xxx
z
x
y
x
x
xx
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
¶w
w
¶
¶w
w
¶
¶w
r
¶t
¶w
r
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
w¶
w
¶
w¶
w
¶
w¶
r
t¶
w¶
r
+++-
=+++
¢
¢
+
¢
¢
+
¢
¢
¢
+
¢
¢
-
¢
=
¢
¢
¢
+
¢
¢
¢
+
¢
¢
¢
¢
+
¢
¢
¢
(18.20)
НГАВТ - Стр 204 из 239
Новосибирская Государственная Академия Водного Транспорта

176
Для подобных процессов
mt
wr
mmtt
wwrr
c cpp c
czzyyxx c c
p
l
=
¢
=
¢
=
¢
=
¢
=
¢
=
¢
=
¢
=
¢
/",/",/"
,/"/"/",/",/"
Если выразить переменные второй системы через переменные пер-
вой системы и множители подобного преобразования, то получится
)(
)(
©
2
2
2
2
2
2
2
2
zyxc
cc
x
p
c
c
gcc
zyxc
cc
с
сс
xxx
l
l
p
g
z
x
y
x
x
x
l
x
¢
¢
+
¢
+
¢
+
¢
¢
-
¢¢
=
¢
¢
¢
+
¢
¢
¢
+
¢
¢
¢
¢
+
¢
¢
¢
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
w¶
w
¶
w¶
w
¶
w¶
r
t¶
w¶
r
wm
r
wr
t
wr
(18.21)
Тождественность уравнений (18.20) и (18.21) возможно при сле-
дующем условии:
22
llpgl
cccccccccccсс ////
wmrwrtwr
====
Из равенства
l
ccccсс //
2
wrtwr
= получается индикатор подобия
1=
l
cсс /
tw
и число гомохронности
l
Но
wt
=
Из условия
gl
cccсс
rwr
=/
2
получается индикатор подобия
1
2
=
w
ccс
lg
/ , которому соответствует число Фруда
2
w
gl
Fr =
Следующее равенство
lpl
cccсс // =
2
wr
даёт индикатор подобия
1
2
=)/(
wr
ccс
p
и число Эйлера
2
rw
p
Eu =
Из условия
22
ll
ccccсс //
wmwr
= следует индикатор подобия
1=
mwr
cccс
l
/ и число Рейнольдса
,
n
w
l
Re =
НГАВТ - Стр 205 из 239
Новосибирская Государственная Академия Водного Транспорта
177
где
rmn
/= - кинематическая вязкость.
Из полученных чисел подобия определяющим в гидродинамиче-
ских задачах является число Эйлера
).,,( ReFrHo fEu = (18.22)
Для стационарных гидродинамических процессов, когда фактор
времени не имеет значения, выражение (18.22) упростится
)(Re fEu = (18.23)
При естественной конвекции скорость потока определить чрезвы-
чайно сложно, поэтому часто число Фруда преобразуют в более удобное
число Грасгофа, которое равно произведению числа Фруда на квадрат
числа Рейнольдса и отношение плотностей свободно движущейся сре-
ды:
t
gl
t
lgl
ReFrGr D×=D=-=
2
3
2
2
0
2
n
bb
n
w
w
rrr
)(/)( , (18.24)
где
b
- температурный коэффициент объемного расширения жидкости.
Замена отношения плотностей произведением температурного объ-
емного коэффициента на разность температур объясняется тем, что
причиной естественной конвекции является разность плотностей жидко-
сти, которая образуется из-за изменения температуры.
Анализ уравнения сплошности (18.17) показывает, что новых чисел
подобия, кроме тех, что получены из уравнений энергии, движения и
теплообмена, это выражение не дает.
18.6 Тепловое подобие
Ранее, в главе 16, было показано, что из дифференциального урав-
нения, описывающего процесс теплообмена на границе между жидко-
стью и стенкой, получается число Нуссельта
l
a
l
Nu =
Уравнения, описывающие процесс энергообмена в потоке жидко-
сти, для двух подобных систем
."
"
"
"
""
",
xx
x
tt
x
t
a
x
tt
x
t
a
w
¶
¶
¶t
¶
¶
¶
w
¶
¶
t¶
¶
¶
¶
+=
¢
¢
¢
¢
+
¢
¢
=
¢
¢
¢
2
2
2
2
Множители подобных преобразований равны
НГАВТ - Стр 206 из 239
Новосибирская Государственная Академия Водного Транспорта

178
t
tt
c caa ctt cxx
atl
==
¢
=
¢
=
¢
/",/",/",/"
Переменные второй системы выражаются через переменные пер-
вой системы и множители подобного преобразования:
x
l
tt
l
ta
x
t
c
cc
t
c
c
x
t
a
c
cс
w
¶
¶
t¶
¶
¶
¶
w
t
¢
¢
¢
+
¢
¢
=
¢
¢
¢
2
2
2
Условия подобия определяются равенством
lttlt
ccccccc //
wt
==
2
a
с
Из первого равенства следует индикатор подобия 1
2
=
la
ccс /
t
и
уже знакомое (см. п.18.3) число Фурье
2
l
a
Fo
t
=
Из второго равенства получается индикатор подобия
1=
al
cсс /
w
и число Пекле
a
l
Pe
w
=
При делении числа Пекле на число Рейнольдса получается новый
безразмерный комплекс - число Прандтля:
aPe/RePr /
n
==
Условия теплового подобия процессов в общем виде выглядит так:
)
0
ll/Pr,Fo,Re,Gr,(Ho, fNu = (18.25)
Для стационарных процессов числа подобия, имеющие в своем со-
ставе время, не являются определяющими, и уравнение (6.23) в этом
случае упрощается
)/(
0
llPr,Re,r,G fNu = (18.26)
При свободной конвекции, когда вынужденное движение отсутст-
вует, число Рейнольдса, характеризующее этот режим, отсутствует
)/,,(
0
llPrGr fNu = (18.27)
Конкретный вид критериальных зависимостей для различных слу-
чаев конвективного теплообмена дан ранее в главе 17 .
НГАВТ - Стр 207 из 239
Новосибирская Государственная Академия Водного Транспорта
179
19 Теплопередача при конвективном теплообмене
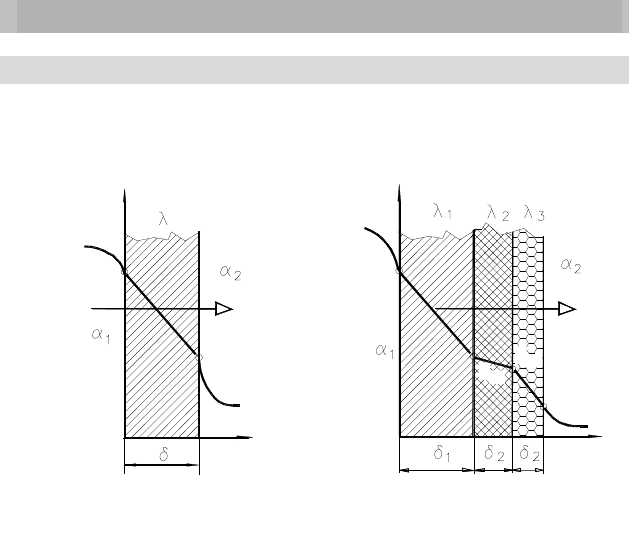
19.1 Теплопередача через плоскую стенку
Если плоская стенка толщиной
d
и теплопроводностью
l
разделяет
две жидкостные или газовые среды, имеющие разные температуры, то
при этом возникает тепловой поток от горячей среды к холодной (рису-
нок 19.1,а).
Плотность теплового потока, передаваемого от горячей среды к
стенке, составляет
)(
1
1
c
ttq -
1
=
a
, (19.1)
где
1
a
- коэффициент теплоотдачи от горячей среды к стенке,
1
t - темпе-
ратура горячей среды,
1c
t - температура стенки.
Если стенка не ограничена по высоте и ширине, то в условиях ста-
ционарного режима через любую изотермическую поверхность в стенке
будет передаваться один и тот же тепловой поток
dl
/)(
21 cc
ttq -= , (19.2)
где
2c
t - температура стенки со стороны холодной cреды.
Рисунок 19.1
t
t
t
q
x
c1
c2
a)
б)
c2
t
t
c1
t
x
q
t
t
c3
c4
1
2
t
t
t
2
t
1
НГАВТ - Стр 208 из 239
Новосибирская Государственная Академия Водного Транспорта

180
При теплоотдаче от стенки к холодной среде плотность теплового
потока равна
)(
222
ttq
c
-=
a
, (19.3)
где
2
a
- коэффициент теплоотдачи от стенки к холодной среде,
2
t - тем-
пература холодной cреды.
При решении уравнений (19.1-19.3) относительно разности темпе-
ратур, получается следующее:
222
21
111
a
ld
a
/
,/
,/
qtt
qtt
qtt
c
cc
c
=-
=-
=
-
(19.4)
Сложение левых и правых частей уравнений (19.4) позволяет опре-
делить зависимость плотности теплового потока от параметров теплопе-
редачи:
)(
///
21
21
21
11
ttк
tt
q -=
++
-
=
alda
, (19.5)
где коэффициент теплопередачи равен
21
11
1
alda
/// ++
=к (19.6)
В случае теплопередачи через n-слойную плоскую стенку (рисунок
19.1,б) коэффициент теплопередачи равен
å
=
=
++
=
ni
i
ii
к
1
21
11
1
alda
/)/(/
, (19.7)
где
ii
ld
, - толщина и теплопроводность i-го слоя.
Величина, обратная коэффициенту теплопередачи, называется пол-
ным термическим сопротивлением:
222111
111
aldlda
/...//// +++== кR (19.8)
Температуры на наружных поверхностях стенки определяются по
формулам
221
111
a
a
/
,/
)(
qtt
qtt
nc
c
+=
-
=
+
(19.9)
Для определения температуры на границе между i-м и (i+1)-м
слоями используется формула
НГАВТ - Стр 209 из 239
Новосибирская Государственная Академия Водного Транспорта
181
)/...//(
)( ii
qt
ic
t
ldlda
++-=
+ 111
1
11
(19.10)
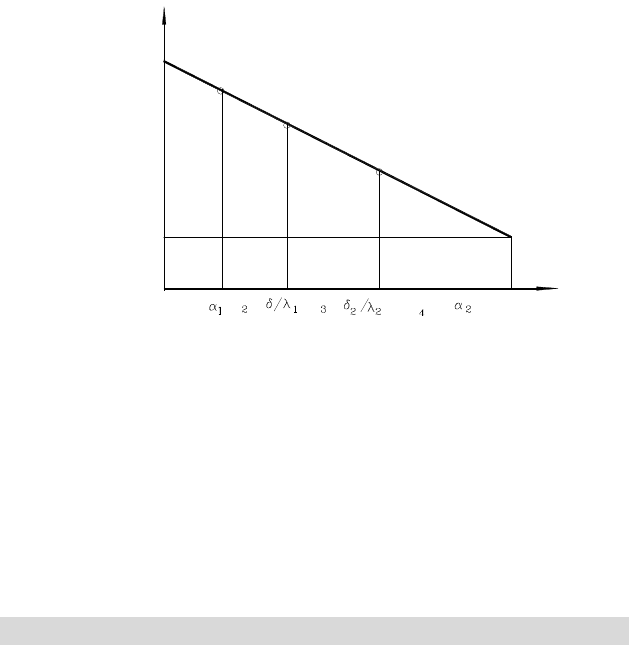
Температуры на стыках между слоями могут быть определены
графическим методом (рисунок 19.2). Для этого на горизонтальной оси
последовательно откладываются значения частных термических сопро-
тивлений
./.../,/,/
212231121
11
aldlda
====
+n1
R R R R , ( 19.11)
а на температурной оси откладываются значения температур горячей и
холодной сред. Точки 1 и 2 соединяются прямой линией. Пересечение
этой линии с восстановленными перпендикулярами с оси R дает значе-
ния искомых температур.
19.2 Теплопередача через цилиндрическую стенку
Особенность теплопередачи через цилиндрическую стенку заклю-
чается в том, что поверхности теплообмена снаружи и внутри трубы
различны. Исходя из схемы передачи теплоты, представленной на ри-
сунке 19.3,а, можно записать для теплового потока, передаваемого через
цилиндрическую стенку, следующие формулы:
Рисунок 19.2
t
t
t
t
t
R
t
R=1/ R
=
R =
R =1/
1
2
c1
c2
c3
НГАВТ - Стр 210 из 239
Новосибирская Государственная Академия Водного Транспорта
