Колпаков Б.А., Лебедев Б.О. Техническая физика. Часть 1 - Теплофизические основы судовой энергетики
Подождите немного. Документ загружается.

166
щими 100-150 К)кВт/(м ×
2
. При пленочной конденсации, которая чаще
всего происходит в теплообменных аппаратах, коэффициент теплоотда-
чи на порядок меньше. Это объясняется тем, что образующаяся на ох-
лаждающей поверхности плёнка создаёт значительное термическое
сопротивление и ухудшает теплообмен между паром и стенкой.
Движение пленки под действием гравитационных сил может быть
ламинарным и турбулентным. Характер движения на вертикальной пла-
стине или трубе характеризуется безразмерным числом
Htt
g
r
Z
cs
×-××= )()(
,330
2
n
rn
l
, (17.24)
где Н - высота стенки, м.
При Z<2300 движение пленки ламинарное и для этого случая рас-
четная формула для среднего по высоте коэффициента теплоотдачи
имеет вид:
t
Z
ДtH
rсс
,
ea
××
180
950
,
= , (17.25)
При Z>2300 течение пленки ламинарное вверху и турбулентное
внизу. Для среднего по высоте коэффициента теплоотдачи используется
формула
331250
2250
,,
][, )/Pr2300)(Pr(Z0,069Pr53
tH
r
cf
0,5
-+
D
=
rn
a
(17.26)
Если конденсация пара происходит на горизонтальных трубах, то
для ламинарного режима, преимущественного в этом случае, рекомен-
дуется такое выражение:
t
t
d
rg
e
n
rl
a
×
D
=
250
3
7250
,
)(, , (17.27)
где d - наружный диаметр трубы, м.
Поправка, учитывающая зависимость физических свойств конден-
сата от температуры в формулах (17.25 и 17.27), определяется по фор-
муле
12503 ,
)]/()/[(
cct
mmlle
×= (17.28)
Физические параметры, входящие в формулы (17.24-17.28) и не
имеющие индексов, определяются при температуре насыщения. Те па-
раметры, которые имеют индекс “с”, принимаются при температуре
стенки.
НГАВТ - Стр 171 из 239
Новосибирская Государственная Академия Водного Транспорта
167
В том случае, когда конденсируется перегретый пар, в формулы
(17.25-17.27) вместо r подставляется значение )(
cpp
ttcr -+ , где
p
c -
изобарная удельная теплоемкость перегретого пара, а
p
t - температу-
ра перегретого пара.
При конденсации влажного пара со степенью сухости х в формулы
(17.25-17.27) вместо r подставляется х· r.
18 Дифференциальные уравнения
теплопроводности и конвективного
теплообмена
18.1 Дифференциальное уравнение теплопроводности
В соответствии с первым законом термодинамики теп-
лота, передаваемая твёрдому телу из окружающей среды,
при отсутствии работы деформации полностью трансфор-
мируется во внутреннюю энергию тела.
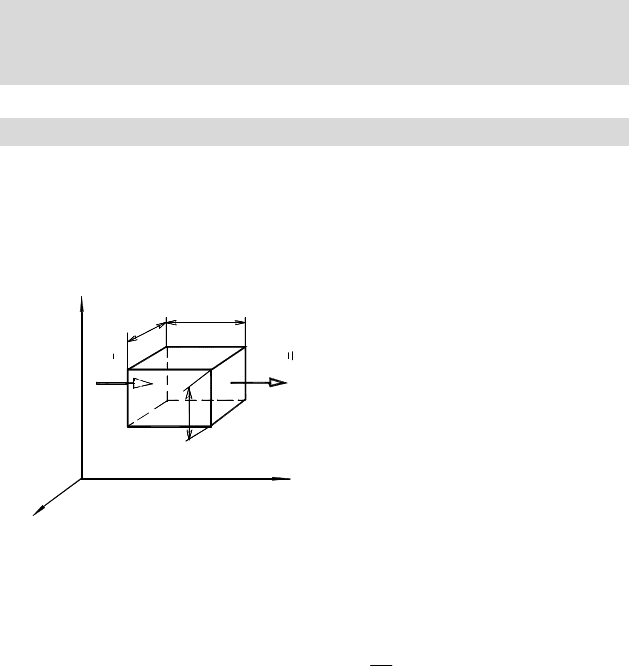
Уравнение теплового ба-
ланса для элемента с величиной
рёбер dzdydx ,, (рисунок 18.1) в
однородном твёрдом теле имеет
вид:
dUQQQ
zyx
=++
ddd
, (18.1)
где
zyx
QQQ
ddd
,, - элементар-
ная теплота, передаваемая через
грани выделенного элемента в
направлении осей x,y,z ; dU -
изменение внутренней энергии
элемента.
В направлении оси x через грань dydz за время d
t
поступает в со-
ответствии с законом Фурье теплота
t
¶
¶
ld
d
x
t
dydzQ
x
-=
¢
Рисунок 18.1
z
x
dx
dz
Q
Q
y
dy
б
б
НГАВТ - Стр 172 из 239
Новосибирская Государственная Академия Водного Транспорта
168
За то же время через противоположную грань, расположенную на
расстоянии dx от первой и имеющую температуру dxxtt )/(
¶¶
+ , из
элемента передается теплота
t
¶
¶
¶
¶
ld
ddx
x
t
t
x
dydzQ
x
)( +-=
¢¢
Результирующая теплота, подведенная теплопроводностью к эле-
менту в направлении оси х, равна
t
¶
¶
lddd
dxdydzd
x
t
QQQ
xxx
2
2
=
¢¢
-
¢
= (18.2)
Аналогично определяется результирующая теплота в направле-
нии осей y и z :
t
¶
¶
ld
t
¶
¶
ld
dxdydzd
z
t
Q
dxdydzd
y
t
Q
z
y
2
2
2
2
=
=
(18.3)
Изменение внутренней энергии элемента составляет
t
¶t
¶
rd
d
t
dVcU = (18.4)
C учетом (18.2-18.4) уравнение (18.1) имеет вид:
t¶t¶rt¶¶¶¶¶¶l
dtdVcdVdztytxt )/()///( =++
222222
(18.5)
После сокращений в уравнении (18.5) получается:
)(
2
2
2
2
2
2
z
t
y
t
x
t
c
t
¶
¶
¶
¶
¶
¶
r
l
¶t
¶
++= (18.6)
Выражение (18.6) называют дифференциальным уравнением тепло-
проводности. Его записывают и в таком виде:
ta
t
2
Ñ=
¶t
¶
, (18.7)
где
r
l
с
а = - коэффициент температуропроводности, характеризую-
щий темп изменения температуры;
2
2
2
2
2
2
2
z
t
y
t
x
t
t
¶
¶
¶
¶
¶
¶
++=Ñ - оператор Лапласа.
НГАВТ - Стр 173 из 239
Новосибирская Государственная Академия Водного Транспорта

169
Уравнение (18.7) описывает в самом общем виде процесс теплопро-
водности и устанавливает связь между временными и пространственны-
ми изменениями температуры тела. Для его решения применительно к
определенной задаче необходимо математическое описание конкретных
условий, называемых условиями однозначности, которые включают:
временные или начальные условия, определяющие распределение
температуры в теле в начальный момент;
геометрические условия, характеризующие форму и размеры тела;
физические условия, задаваемые теплофизическими параметрами
вещества, составляющего рабочее тело;
граничные условия, определяющие характер взаимодействия тела с
окружающей средой на границе соприкосновения.
Начальные условия имеют смысл при нестационарной теплопро-
водности и обычно задаются законом распределения температур по
всему объему тела для момента времени
t
= 0.
Граничные условия могут быть заданы несколькими способами.
Если для любого момента времени известно распределение темпе-
ратур на границе тела, то это называют граничными условиями первого
рода.
При граничных условиях второго рода задаётся поверхностная
плотность теплового потока (а, следовательно, и температурный гради-
ент) в каждой точке поверхности тела для любого момента времени.
Температура на поверхности тела при этом неизвестна.
Граничные условия третьего рода предполагают, что известна
температура окружающей среды и закономерность взаимосвязи между
этой температурой и температурой тела. В условиях конвективного
теплообмена связующим является уравнение Ньютона-Рихмана.
Решение дифференциального уравнения теплопроводности совме-
стно с условиями однозначности позволяет получить температурное
поле исследуемого тела для любого частного случая в любой момент
времени. Такое аналитическое решение позволяет в ряде случаев изба-
виться от проведения сложных и дорогостоящих экспериментальных
работ.
18.2 Распределение температур в однослойной
плоской стенке
НГАВТ - Стр 174 из 239
Новосибирская Государственная Академия Водного Транспорта

170
Пусть теплота передается через плоскую стенку (рисунок 15.2а)
толщиной
d
. Размеры стенки в направлении осей о-z и o-y не ограниче-
ны. Тепловой поток постоянный и не зависит от времени. Температура
горячей поверхности стенки равна
1с
t , температура холодной поверх-
ности -
2c
t .
Для этого случая одномерной задачи уравнение теплопроводности
(18.7) имеет вид:
0
22
=xt
¶¶
/ (18.8)
При принятых граничных условиях первого рода
(
210 cxcx
tttt ==
==
d
,( ) последовательное интегрирование формулы
(18.8) даёт:
baxt axt +== ,/
¶¶
(18.9)
Выражение (18.9) показывает линейную зависимость температуры
по толщине стенки.
Для определения констант интегрирования используются гранич-
ные условия:
d
d
d
/)(
,,
21
1210
cc
ccxcx
tta
tatt btt
--=
+====
==
После подстановки констант в формулу (18.9) выражение для оп-
ределения температуры в любом сечении стенки предстанет в таком
виде:
x
tt
tt
cc
cx
×
-
-=
d
21
1
, (18.10)
где x - отстояние сечения от начала координат
18.3 Теплопроводность при нестационарном режиме
Нестационарные процессы теплопроводности встречаются при на-
гревании и охлаждении металлических заготовок в литейном и кузнеч-
ном производствах, при обжиге кирпича, при запуске дизельных дизель-
ных или карбюраторных двигателей, при прогреве холодных зданий,
при замерзании рек и водохранилищ и т.д.
Как отмечалось в п 15.1 , нестационарная теплопроводность харак-
теризуется уравнением
)f(x,y,z,t
t
=
НГАВТ - Стр 175 из 239
Новосибирская Государственная Академия Водного Транспорта

171
Указанная зависимость может быть определена из решения диффе-
ренциального уравнения теплопроводности (18.6) при граничных усло-
виях третьего рода методами теории подобия.
Для одномерной нестационарной задачи изменение температуры
по оси х и во времени определяется выражением, полученным из урав-
нения теплопроводности (18.7), которое для этого случая имеет вид:
t
¶
¶
=
¶
¶ t
x
t
а
2
2
Обработка этого выражения методами теории подобия выяв-
ляет число Фурье:
Fo
l
a
c
cc
c
c
c
cс
caacxxcttc
t
x
t
a
t
x
t
a
l
at
l
a
alt
=®=®=
¢
=
¢
=
¢
=
¢
=
=
¢¢
¢
¢
=
¢
¢
¢
222
2
2
2
2
1
t
tt
¶t
¶
¶
¶
t¶
¶
¶
¶
t
t
t
t
;/",/",/",/"
;
"
"
"
"
,
(18.11)
Обработка уравнения (18.11) , характеризующего граничные усло-
вия третьего рода, выявляет число подобия Био:
Bi
l
xx
x
x
c
cc
cc
c
cc
tcc
xd
td
c
сс
cxxcttcс
t
dx
dt
t
xd
td
l
t
l
t
t
l
t
lt
=
¢
¢¢
=®=
¢¢
¢
®=
®=®
¢
D
¢
=
¢
¢
¢
-
¢
=
¢
=
¢
=
¢
=
D=-
¢
D
¢
=
¢
¢
¢
-
l
a
l
a
l
a
a
l
l
a
al
aall
alal
l
a
a
l
a
l
al
,
"
""
"
""
)()(
;/",/",/",/"
;""
"
"
",
11
где l - характерный линейный размер геометрической системы, λ – теп-
лопроводность стенки.
Число Био отличается от числа Нуссельта тем, что оно содержит
теплопроводность материала тела, а не теплопроводность движущейся
около тела жидкой или газообразной среды. Это число определяет соот-
ношение теплоты, переданной конвективным способом, и теплоты,
переданной внутри тела теплопроводностью.
Искомая функция в виде безразмерной температуры определяется в
общем случае выражением
)/,,(/ lxBiFo f
x
=
qq
. (18.12)
НГАВТ - Стр 176 из 239
Новосибирская Государственная Академия Водного Транспорта
172
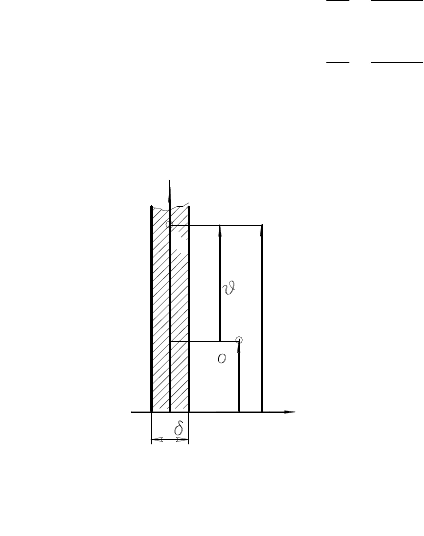
В качестве примера ниже рассматривается процесс охлаждения
равномерно прогретой пластины с начальной температурой t , которая
омывается с обеих сторон жидкостью или газом с температурой
c
t при
коэффициенте теплоотдачи
a
. Размеры пластины в направлении осей y
и z считаются неограниченными, а физические характеристики материа-
ла пластины - теплопроводность
l
, теплоёмкость с и плотность
r
- по-
стоянными.
Решение задачи представляется в виде:
),,(
),,(
BiFo f
tt
tt
BiFo f
tt
tt
c
cцц
c
cпп
2
1
=
-
-
=
=
-
-
=
q
q
q
q
(18.13)
где
цп
tt , - температуры на поверхности и в центральном сечении пла-
стины.
Отсутствие в формулах (18.13) линей-
ного симплекса объясняется тем, что в сред-
ней плоcкости и на поверхности пластины
температуры постоянны и изменяются толь-
ко в направлении оси x.
Теплота, передаваемая пластиной в ок-
ружающую среду за время
t
, равно измене-
нию внутренней энергии пластины за период
охлаждения.
Начальная внутренняя энергия пла-
стины, отсчитанная от внутренней энер-
гии при температуре среды как от нуля,
равна
rdqrd
ActtAcU
c
22
0
=-= )( (18.14)
Отношение теплоты, переданной за период
t
, к началь-
ной внутренней энергии пластины определяется также без-
размерными числами Био и Фурье:
),(/ FoBifUФ
30
=
t
(18.15)
Конкретные решения уравнений (18.13,18.15) обычно представле-
ны в виде графиков или в табличной форме (cм. таблицу 18.1). При ре-
шении конкретной задачи вначале подсчитывают числовые значения
Рису-
нок 18.2
t
t
x
t
2
НГАВТ - Стр 177 из 239
Новосибирская Государственная Академия Водного Транспорта

173
определяющих критериев, а затем, пользуясь таблицей, находят иско-
мые значения.
Решения, аналогичные вышеизложенному, имеются для других
геометрических систем - цилиндрических тел, шаров и др.
Таблица 18.1 - Расчётные зависимости для пластины
Bi 0,00
1
0,01 0,1 0,5 1 4 10 20 50
Fo θ
п
/θ = f
1
(Fo,Bi)
0,05
0,1
0,5
1
2
5
10
20
50
1
1
1
1
0,99
0,98
0,96
1
0,99
0,99
0,98
0,95
0,90
0,82
0,61
1
0,97
0,92
0,83
0,62
0.37
0,14
0,01
1
0,87
0,70
0,46
0,13
0,02
0
1
0,78
0,54
0,31
0,03
0
1
0,98
0,56
0,25
0,06
0
1
0,97
0,46
0,16
0,02
0
1
0,96
0,41
0,13
0,01
0
1
0,95
0,39
0,12
0,01
0
Fo θ
ц
/θ = f
2
(Fo,Bi)
0,02
0,05
0,1
0,5
1
2
5
10
20
50
1
1
1
1
1
1
1
0,99
0,98
0,96
0,99
0,99
0,99
0,99
0,98
0,97
0,95
0,90
0,81
0,60
0,98
0,98
0,97
0,92
0,88
0,79
0,59
0,36
0,13
0,01
0,93
0,89
0,85
0,69
0,56
0,37
0,10
0,01
0
0,86
0,79
0,73
0,51
0,35
0,17
0,02
0
0,59
0,46
0,37
0,17
0,08
0,02
0
0,34
0,23
0,17
0,06
0,02
0
0,19
0,12
0,06
0,01
0
0,08
0,05
0,04
0,01
0
Fo Ф/θ = f
3
(Fo,Bi)
0,02
0,05
0,1
0,5
1
2
5
10
20
0,01
0,02
0,01
0,02
0,05
0,10
0,18
0,01
0,02
0,05
0,10
0,17
0,39
0,62
0,81
0,01
0,03
0,09
0,17
0,31
0,62
0,84
0,93
0,01
0,02
0,05
0,20
0,35
0,59
0,88
0,99
1
0,02
0,04
0,08
0,32
0,53
0,78
0,98
1
0,05
0,12
0,20
0,58
0,81
0,96
1
0,09
0,18
0,27
0,69
0,89
0,98
1
0,12
0,23
0,34
0,75
0,92
0,99
1
НГАВТ - Стр 178 из 239
Новосибирская Государственная Академия Водного Транспорта

174
50 0,04 0,39 0,92 0,99
18.4 Дифференциальные уравнения конвективного
теплообмена
Дифференциальные уравнения конвективного теплообмена учиты-
вают особенности гидродинамики потока и влияние различных факто-
ров на теплообмен между потоком и поверхностью твердого тела.
Гидродинамика потока описывается уравнением движения
вязкой жидкости (уравнением Навье-Стокса) и уравнением неразрыв-
ности (сплошности) потока.
Уравнение движения учитывает влияние сил инерции (левая часть
уравнения), сил вязкостного трения (третье слагаемое в правой части),
сил статического давления (второе слагаемое в правой части) и гравита-
ционных сил (первое слагаемое в правой части). Оно определяет поле
скоростей во времени, а также в пространстве, и в проекции на ось х
имеет следующий вид:
).(
)
2
2
2
2
2
2
zyx
x
p
g
zyx
z
xx
x
z
x
y
x
x
›
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
¶w
w
¶
¶w
w
¶
¶w
¶t
¶w
r
+++-
=+++
›
(
(18.16)
где выделенное скобками в левой части выражение представляет собой
полную или субстанциальную (в пространственных и временных коор-
динатах) производную от скорости
tw
dD
x
/ . С учетом этого
x
x
dx
dp
g
d
D
wmr
t
w
r
2
Ñ+-= (18.16а)
Аналогично записываются уравнения в проекции на оси y и z:
y
y
dx
dp
d
D
wm
t
w
r
2
Ñ+-= (18.16б)
z
z
dx
dp
d
D
wm
t
w
r
2
Ñ+-= (18.16в)
В формулах (18.16):
r
- плотность вязкой жидкости,
zy›
www
,, -
проекции скорости на соответствующие оси x,y и z , p - давление,
m
-
коэффициент динамической вязкости.
НГАВТ - Стр 179 из 239
Новосибирская Государственная Академия Водного Транспорта

175
Уравнение сплошности выводится на основе закона сохранения
массы и говорит о том, что в любом сечении неразрывного потока жид-
кости или газа массовый расход имеет одно и то же значение:
0=+++
¶t
¶
¶
rw¶
¶
rw
¶
¶
rw¶
p
zyx
z
y
x
)(
)(
)(
(18.17)
В основу вывода дифференциального уравнения энергии для дви-
жущегося потока сжимаемой вязкой жидкости положен закон сохране-
ния энергии. Это уравнение определяет изменение температуры жидко-
сти во времени и в пространстве. В отличие от дифференциального
уравнения теплопроводности в уравнении энергии учитывается то об-
стоятельство, что в движущемся потоке температура изменяется не
только за счет нагревания или охлаждения, но и в связи с изменением
положения этой жидкости в пространстве. Этим объясняется появление
в правой части формулы (18.19) субстанциальной производной от ско-
рости:
zyx
z
t
y
t
x
tt
ta
w
¶
¶
w
¶
¶
w
¶
¶
¶t
¶
+++=Ñ
2
(18.19)
Дифференциальное уравнение, описывающее процесс теплооб-
мена на границе жидкости и стенки (16.3) , уже было применено ранее в
п. 16.2.
18.5 Условия гидродинамического подобия
Для двух подобных систем, в которых протекают подобные про-
цессы, записываются уравнения движения
)
"
"
"
"
"
"
("
"
"
"
)"
"
"
"
"
"
"
"
"
("
"
"
"
),(
)(
2
2
2
2
2
2
2
2
2
2
2
2
zyx
x
p
g
zyx
zyx
x
p
g
zyx
xxx
z
x
y
x
x
xx
xxx
z
x
y
x
x
xx
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
¶w
w
¶
¶w
w
¶
¶w
r
¶t
¶w
r
¶
w¶
¶
w¶
¶
w¶
m
¶
¶
r
w
¶
w¶
w
¶
w¶
w
¶
w¶
r
t¶
w¶
r
+++-
=+++
¢
¢
+
¢
¢
+
¢
¢
¢
+
¢
¢
-
¢
=
¢
¢
¢
+
¢
¢
¢
+
¢
¢
¢
¢
+
¢
¢
¢
(18.20)
НГАВТ - Стр 180 из 239
Новосибирская Государственная Академия Водного Транспорта
