Колпаков Б.А., Лебедев Б.О. Техническая физика. Часть 1 - Теплофизические основы судовой энергетики

Подождите немного. Документ загружается.

176

Для подобных процессов

mmtt

wwrr

c cpp c

czzyyxx c c

/",/",/"

,/"/"/",/",/"

Если выразить переменные второй системы через переменные пер-

вой системы и множители подобного преобразования, то получится

)(

zyxc

gcc

zyxc

сс

xxx

¢¢

w¶

t¶

w¶

(18.21)

Тождественность уравнений (18.20) и (18.21) возможно при сле-

дующем условии:

llpgl

cccccccccccсс ////

wmrwrtwr

====

Из равенства

ccccсс //

wrtwr

= получается индикатор подобия

cсс /

и число гомохронности

Но

Из условия

cccсс

rwr

получается индикатор подобия

ccс

/ , которому соответствует число Фруда

Fr =

Следующее равенство

lpl

cccсс // =

даёт индикатор подобия

=)/(

ccс

и число Эйлера

Eu =

Из условия

ccccсс //

wmwr

= следует индикатор подобия

mwr

cccс

/ и число Рейнольдса

Re =

НГАВТ - Стр 181 из 239

Новосибирская Государственная Академия Водного Транспорта

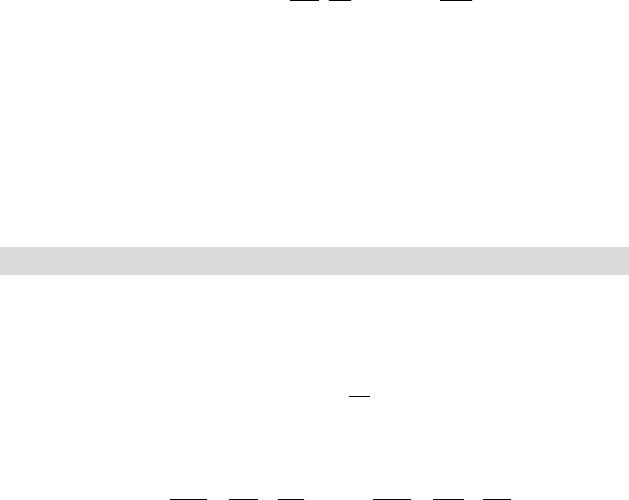
177

где

rmn

/= - кинематическая вязкость.

Из полученных чисел подобия определяющим в гидродинамиче-

ских задачах является число Эйлера

).,,( ReFrHo fEu = (18.22)

Для стационарных гидродинамических процессов, когда фактор

времени не имеет значения, выражение (18.22) упростится

)(Re fEu = (18.23)

При естественной конвекции скорость потока определить чрезвы-

чайно сложно, поэтому часто число Фруда преобразуют в более удобное

число Грасгофа, которое равно произведению числа Фруда на квадрат

числа Рейнольдса и отношение плотностей свободно движущейся сре-

ды:

lgl

ReFrGr D×=D=-=

rrr

)(/)( , (18.24)

где

- температурный коэффициент объемного расширения жидкости.

Замена отношения плотностей произведением температурного объ-

емного коэффициента на разность температур объясняется тем, что

причиной естественной конвекции является разность плотностей жидко-

сти, которая образуется из-за изменения температуры.

Анализ уравнения сплошности (18.17) показывает, что новых чисел

подобия, кроме тех, что получены из уравнений энергии, движения и

теплообмена, это выражение не дает.

18.6 Тепловое подобие

Ранее, в главе 16, было показано, что из дифференциального урав-

нения, описывающего процесс теплообмена на границе между жидко-

стью и стенкой, получается число Нуссельта

Nu =

Уравнения, описывающие процесс энергообмена в потоке жидко-

сти, для двух подобных систем

¶t

t¶

Множители подобных преобразований равны

НГАВТ - Стр 182 из 239

Новосибирская Государственная Академия Водного Транспорта

178

c caa ctt cxx

atl

/",/",/",/"

Переменные второй системы выражаются через переменные пер-

вой системы и множители подобного преобразования:

cс

t¶

Условия подобия определяются равенством

lttlt

ccccccc //

Из первого равенства следует индикатор подобия 1

ccс /

уже знакомое (см. п.18.3) число Фурье

Из второго равенства получается индикатор подобия

cсс /

и число Пекле

При делении числа Пекле на число Рейнольдса получается новый

безразмерный комплекс - число Прандтля:

aPe/RePr /

Условия теплового подобия процессов в общем виде выглядит так:

)

ll/Pr,Fo,Re,Gr,(Ho, fNu = (18.25)

Для стационарных процессов числа подобия, имеющие в своем со-

ставе время, не являются определяющими, и уравнение (6.23) в этом

случае упрощается

)/(

llPr,Re,r,G fNu = (18.26)

При свободной конвекции, когда вынужденное движение отсутст-

вует, число Рейнольдса, характеризующее этот режим, отсутствует

)/,,(

llPrGr fNu = (18.27)

Конкретный вид критериальных зависимостей для различных слу-

чаев конвективного теплообмена дан ранее в главе 17 .

НГАВТ - Стр 183 из 239

Новосибирская Государственная Академия Водного Транспорта

156

17 Частные случаи конвективного

теплообмена

17.1 Теплообмен при движении жидкости в трубах

Гидродинамические исследования показывают, что в гладких ци-

линдрических трубах при значениях числа Рейнольдса менее 2200 поток

движется ламинарно, а при

10³Re наблюдается развитый турбу-

лентный режим течения. Промежуточный между ламинарным и турбу-

лентным, так называемый переходный режим течения, является неус-

тойчивым и зависящим от незначительных внешних воздействий. Сле-

дует отметить, что границы перехода от одного режима к другому не

зависят от того, какая жидкость или газ протекают в трубах - это может

Рисунок 17.1

а)

б)

max

НГАВТ - Стр 184 из 239

Новосибирская Государственная Академия Водного Транспорта

157

быть вода, воздух, бензин и пр. Поэтому в дальнейшем словом “жид-

кость” будет определяться любая текучая среда.

На рисунке 17.1 показано, как изменяется скорость по поперечно-

му сечению трубы при ламинарном (а) и турбулентном (б) режимах

движения потока. Для ламинарного движения отношение средней ско-

рости

к максимальной

составляет примерно 0,5 , а для турбу-

лентного режима, где изменение скорости потока происходит в основ-

ном в пределах гидродинамического пограничного слоя, это отношение

равно » 0,8. Различие в гидродинамике потока, естественно, отражается

и на процессе конвективного теплообмена.

Для ламинарного режима

25010430

150

,,,

)(,

cfff

0,33

/PrPrGrPrReNu = , (17.1)

для развитого турбулентного режима

250

0210

0,43

0,8

/Pr(PrPrReNu = , (17.2)

для переходного режима

250,

)

0,43

/Pr(PrPrKoNu ×= , (17.3)

где численное значение комплекса Ко определяется из таблицы 17.1 в

зависимости от числа Рейнольдса.

Таблица 17.1

Re * 10

2,1

2,2 2,3 2,4 2,5 3,0 4,0 5,0 7,5 10

Ko 1,9

2,2 3,3 3,8 4,4 6,0 10,3 15,5 24,4 33,3

В вышеприведенных формулах индекс “f” показывает, что физиче-

ские характеристики жидкости (кинематическую вязкость, плотность,

теплоемкость и др.), входящие в числа подобия, следует определять при

температуре жидкости, а индекс “с” говорит об определяющей темпера-

туре стенки. Определяющей скоростью в этих формулах принята сред-

няя по сечению скорость потока, а определяющим линейным размером

является внутренний диаметр трубы d.

Присутствие в формулах (17.1-17.3) отношения чисел Прандтля

объясняется тем, что при нагревании среды, текущей в трубе, при про-

чих равных условиях теплоотдача интенсивнее, чем при охлаждении.

Так как для воздуха и двухатомных газов число Прандтля практи-

чески постоянно и равно 0,71, формулы (17.1) и (17.2) представляются в

более простом виде:

10330

130

, GrReNu

×= (17.4)

НГАВТ - Стр 185 из 239

Новосибирская Государственная Академия Водного Транспорта

158

0180

Re,

Nu = (17.5)

Формулы (17.1-17.5) применимы не только для круглых труб, но и

для труб любого поперечного сечения - квадратного, треугольного или

эллипсного. Для некруглых труб за определяющий линейный размер

принимается эквивалентный диаметр:

PАd

/4= ,

где А - площадь поперечного сечения канала, Р - смоченный периметр

сечения.

При теплообмене между потоком и стенкой в коротких трубах, ко-

гда длина трубы L меньше 50-ти диаметров, полученное значение числа

Нуссельта следует умножить на поправочный коэффициент, значение

которого приведены в таблице 17.2.

Таблица 17.2

L/d 1 2 5 10 15 20 30 40 50

Re=2 ·10

1,90 1,70 1,44 1,28 1,18 1,13 1,05 1,02 1,00

Re=2 ·10

1,51 1,40 1,27 1,18 1,13 1,10 1,05 1,02 1,00

Re=1 ·10

1,28 1,22 1,15 1,10 1,08 1,06 1,03 1,02 1,00

При движении жидкости в винтовых змеевиках (рисунок 17.2,а)

возникает дополнительная циркуляция потока, что приводит к увеличе-

нию коэффициента тепло-

отдачи. В области разви-

той турбулентности при

значениях

280

18500

)/(Re Dd

> ,

где D – диаметр спирали,

коэффициент теплоотда-

чи, определяемый для

прямой трубы, умножает-

ся на поправочный коэф-

фициент

, который под-

считывается по формуле

= 1 + 3,6 d/D (7.6)

При движении потока в кольцевых каналах (рисунок 17.2,б) теп-

лоотдача определяется выражением

Рисунок 17.2

а) б)

НГАВТ - Стр 186 из 239

Новосибирская Государственная Академия Водного Транспорта

159

180

2504080

0170

,,,,

)/(PrPrPrRe, dd)/(Nu

cffff

= , (17.7)

где d

– внутренний диаметр канала, d

– наружный диаметр канала, а

определяющим размером является разность диаметров d = d

– d

17.2 Теплоотдача при поперечном обтекании

одиночной трубы

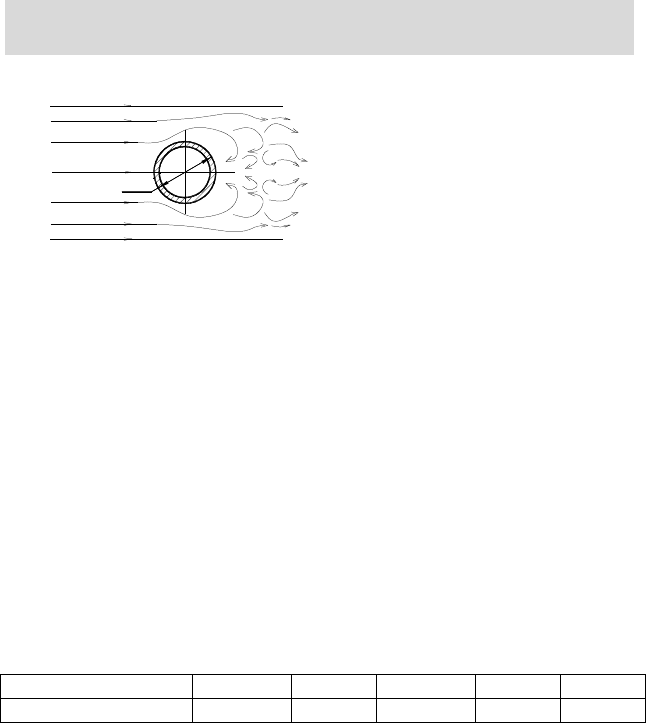
Картина обтекания потоком

цилиндрической трубы показана

на рисунке 17.3. Так как ско-

рость обтекания в различных

точках цилиндра неодинакова,

коэффициент теплоотдачи по

периметру будет так же разли-

чен.

В практических расчетах

локальные значения коэффици-

ента теплоотдачи требуются редко, поэтому ниже приведены формулы,

справедливые для осредненных значений чисел Нуссельта и, соответст-

венно, коэффициентов теплоотдачи для всей поверхности трубы при:

25053

2503

25010210

501010

)/Pr(PrPrRe,Nu Re

,)/Pr(PrPrRe,Nu Re

0,38

0,6

fff

0,38

0,5

fff

=×-=

=-=

(17.8)

В этих формулах определяющими приняты:

- скорость набегающего потока,

- температура набегающего потока,

- наружный диаметр трубы.

В том случае, когда угол атаки набегающего потока по отношению

к оси трубы отличен от 90°, значение числа Нуссельта следует умно-

жить на поправочный коэффициент, указанный в таблице 17.3.

Таблица 17.3

Угол атаки, град. 90 70 50 30 20

Коэффициент 1,00 0,98 0,83 0,64 0,60

Рисунок 17.3

НГАВТ - Стр 187 из 239

Новосибирская Государственная Академия Водного Транспорта

160

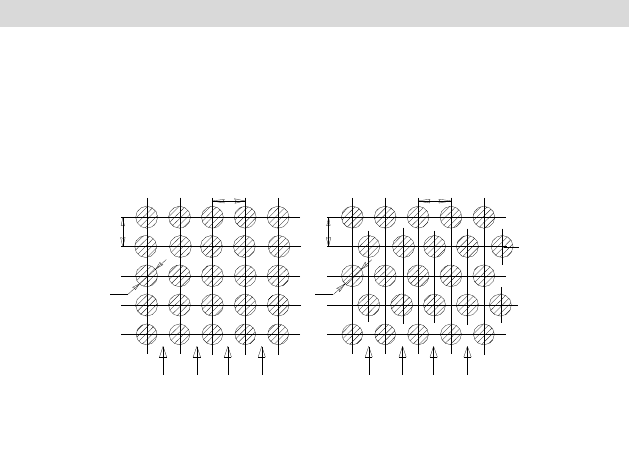
17.3 Теплоотдача в пучках труб

Многие теплообменные аппараты состоят не из одиночных по-

верхностей или труб, а составлены из трубных пучков. Расположение

труб в пучке относительно друг к другу может быть различным, и от

этого зависят условия обтекания труб, что влияет на коэффициент теп-

лоотдачи. Чаще всего рассматривают шахматное (а) и коридорное (б)

расположение труб в пучке (рисунок 17.4). Поперечный S

и продоль-

ный S

шаги между труб зависят от конструктивных особенностей теп-

лообменника и выбираются в каждом конкретном случае по различным

опытным данным.

Для шахматного пучка рекомендуются следующие расчетные вы-

ражения:

2505

250

25020

2503

0210102

400

210210

350

210210

6010

;)/(,

0,36

0,84

0,36

0,6

0,36

0,6

0,36

0,5

/Pr(PrPrReNu Reпри

)/Pr(PrPrReNu

SSи Reпри

)/Pr(PrPrReSSNu

SSи Reпри

)/Pr(PrPrReNu Re при

=×>

>×-=

<×-=

=£

(17.9)

В случае коридорного расположения труб в пучке используются

следующие формулы:

Рисунок 17.4

d d

а)

б)

НГАВТ - Стр 188 из 239

Новосибирская Государственная Академия Водного Транспорта

161

)./Pr(PrPr0,02ReNu 102Reпри

/Pr)(PrPr0,27ReNu 10210Reпри

;)/Pr(PrPr0,52ReNu 10Reпри

0,36

0,84

0,36

0,63

0,25

0,360,5

=×>

=×-=

;

,250

(17.10)

В этих формулах определяющим размером является наружный

диаметр трубы, а определяющей скоростью - скорость потока в самом

узком сечении пучка. Симплекс

SS / характеризует особенности

геометрии пучка.

Все вышеприведенные формулы справедливы для третьего и по-

следующих рядов труб, где поток установившийся и коэффициент теп-

лоотдачи постоянный. Коэффициент теплоотдачи для труб первого ряда

составляет 0,6 от найденного по формулам (17.9-17.10). Для труб второ-

го ряда этот поправочный коэффициент равен 0,7 для шахматного рас-

положения труб и 0,9 - для коридорного. Средний коэффициент тепло-

отдачи для всего пучка, состоящего из z рядов, определяется по форму-

лам: для шахматного пучка - ,/),( zz 70-=

для коридорного пучка

- zz /),( 50-=

(17.11)

17.4 Теплоотдача при вынужденном движении

потока вдоль горизонтальной пластины

При ламинарном режиме течения потока (при

104 ×<Re ) реко-

мендуется следующая формула:

250

660

0,43

0,5

/Pr(PrPrReNu = . (17.12)

В случае турбулентного движения жидкости (при

10>Re ):

250

030

, )/Pr(PrPr7ReNu

0,43

0,8

= . (17.13)

Определяющим линейным размером в этих формулах является

длина пластины в направлении потока, а определяющей скоростью -

средняя скорость потока.

17.5 Теплоотдача при естественной конвекции

Если температура стенки превышает температуру жидкости или

газа, находящихся около стенки, то в самой среде возникает естествен-

ная конвекция из-за различия в плотности неодинаково нагретой среды.

НГАВТ - Стр 189 из 239

Новосибирская Государственная Академия Водного Транспорта

162

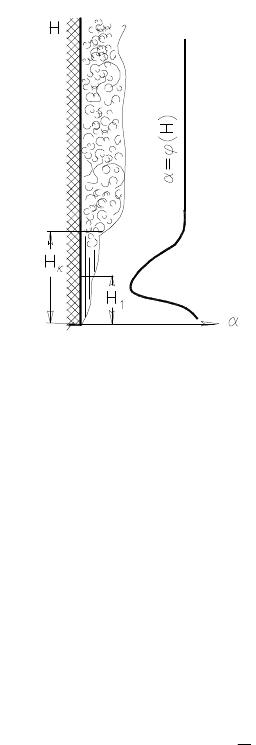
На рисунке 17.5 показано, как изменяется коэффициент теплоотда-

чи при свободной конвекции около вертикальной пластины или трубы.

На начальном участке

H поток дви-

жется ламинарно. По мере увеличения тол-

щины ламинарного слоя возрастает терми-

ческое сопротивление и это приводит к

уменьшению коэффициента теплоотдачи.

Затем под влиянием вязкостных сил лами-

нарный слой постепенно разрушается, пере-

ходя в турбулентный. На какой-то высоте

H турбулентный поток стабилизируется и

коэффициент теплоотдачи остается посто-

янным.

При числе Рэлея менее

10 процесс

протекает в области, соответствующей вы-

соте

H и для этого режима теплоотдача

определяется по формуле

250250

760

, )/Pr(PrRaNu

cfff

. (17.14)

При значениях

10>Ra наблюдается и ламинарное, и турбулент-

ное течение.

В этом случае вначале определяется критическая высота

3303

)]/([

tgaH D=

, (17.15)

и для определения коэффициента теплоотдачи a

на этом участке ис-

пользуется формула (17.14). На оставшемся участке с турбулентным

режимом движения потока коэффициент теплоотдачи

определяется

по формуле

,, 250330

150 )/Pr(PrRaNu

cfff

(17.16)

Средний по высоте коэффициент теплоотдачи при наличии лами-

нарного и турбулентного участков пограничного слоя на вертикальной

поверхности определяется по выражению

,/)]([ HHHH

kТkл

-+=

aaa

(17.17)

где

tл

, - коэффициенты теплоотдачи ламинарного и турбулентно-

го участков, подсчитанные по формулам (17.14,17.16).

Рисунок 17.5

НГАВТ - Стр 190 из 239

Новосибирская Государственная Академия Водного Транспорта