Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.


˙x
g
(t)=V
x
− V
y
ψ + V
z
ϕ;
˙y
g
(t)=V
x
ψ + V
y
− V
z
θ;
˙z
g
(t)=−V
x
ϕ − V
y
θ + V
z
;
˙
θ(t)=
1
1+ψθ
(ω
x
+ ω
x
ψθ − ω
y
ψ + ω
z
ψ
2
);
˙ϕ(t)=
1
1+ψθ
(ω
y
− ω
z
ψ);
˙
ψ(t)=
1
1+ψθ
(ω
z
+ ω
y
θ);
x
g
y
z
z
g
θ
ϕ ψ
•
•
•

•
•
•
•
•
˙
H(t)=const,
H
α = ϑ − θ = α ,
α = const
α
α
V

˙x
1
(t)=−x
3
x
5
+ x
2
x
6
− g sin x
10
+(1/m) u
1
;
˙x
2
(t)=−x
1
x
6
+ x
3
x
4
− g cos x
11
cos x
10
+(1/m) u
2
;
˙x
3
(t)=−x
2
x
4
+ x
1
x
5
+ g sin x
11
cos x
10
+(1/m) u
3
;
˙x
4
(t)=a
2
x
5
x
6
+ a
1
u
4
;˙x
5
(t)=a
4
x
4
x
6
+ a
3
u
5
;˙x
6
(t)=a
6
x
4
x
5
+ a
5
u
6
;
˙x
7
(t)=x
1
cos x
12
cos x
10
+x
2
(sin x
11
sin x
12
−cos x
11
cos x
12
sin x
10
)+
+ x
3
(cos x
11
sin x
12
+sinx
11
cos x
12
sin x
10
);
˙x
8
(t)=x
1
sin x
11
+ x
2
cos x
11
cos x
10
− x
3
sin x
11
cos x
10
;
˙x
9
(t)=−x
1
sin x
12
cos x
10
+x
2
(sin x
11
cos x
12
+cosx
11
sin x
12
sin x
10
)+
+ x
3
(cos x
11
cos x
12
−sin x
11
sin x
12
sin x
10
);
˙x
10
(t)=x
5
sin x
11
+ x
6
cos x
11
;˙x
11
(t)=x
4
− tg x
10
(x
5
cos x
11
− x
6
sin x
11
);
˙x
12
(t)=x
5
cos x
11
cos x
10
− x
6
sin x
11
cos x
10
,
x
1
= V
x
,x
2
= V
y
,x
3
= V
z
x
4
= ω
x
,x
5
= ω
y
,x
6
= ω
z

x
7
= X, x
8
= Y, x
9
= Z
x
10
= ϑ, x
11
= γ, x
12
= χ
u
1
= F
x
,u
2
= F
y
,u
3
= F
z
u
4
=
M
x
,u
5
= M
y
,u
6
= M
z
g m
a
1
=1/I
x
,a
2
=(I
y
− I
z
)/I
x
,a
3
=1/I
y
,a
4
=(I
z
− I
x
)/I
y
,a
5
=1/I
z
,a
6
=
(I
x
− I
y
)/I
z
I
x
,I
y
,I
z
u
•
•
Ψ
1
= x
1
− x
∗
1
;Ψ
2
= x
2
− ϕ
2
;
Ψ
3
= x
3
− ϕ
3
;Ψ
4
= x
4
− ϕ
4
;
Ψ
5
= x
5
− ϕ
5
;Ψ
6
= x
6
− ϕ
6
.
T
m
˙
Ψ
m
(t)+Ψ
m
=0,m=1, 2,...,6,
T
m
ϕ
i
,i=2, 3,...,6,
Ψ
m
=0
T
m
> 0.
Ψ
1
=0
x
∗
1
OX

x
∗
1
= V cos x
10
,
V
Ψ
m
=0,m=1, 2,...,6
x
1
− x
∗
1
=0; x
2
− ϕ
2
=0;
x
3
− ϕ
3
=0; x
4
− ϕ
4
=0;
x
5
− ϕ
5
=0; x
6
− ϕ
6
=0
˙x
7
(t)=x
∗
1
cos x
12
cos x
10
+ϕ
2
(sin x
11
sin x
12
−cos x
11
cos x
12
sin x
10
)+
+ ϕ
3
(cos x
11
sin x
12
+sinx
11
cos x
12
sin x
10
);
˙x
8
(t)=x
∗
1
sin x
11
+ ϕ
2
cos x
11
cos x
10
− ϕ
3
sin x
11
cos x
10
;
˙x
9
(t)=−x
∗
1
sin x
12
cos x
10
+ϕ
2
(sin x
11
cos x
12
+cosx
11
sin x
12
sin x
10
)+
+ ϕ
3
(cos x
11
cos x
12
− sin x
11
sin x
12
sin x
10
);
˙x
10
(t)=ϕ
5
sin x
11
+ ϕ
6
cos x
11
;
˙x
11
(t)=ϕ
4
− tg x
10
(ϕ
5
cos x
11
− ϕ
6
sin x
11
);
˙x
12
(t)=ϕ
5
cos x
11
cos x
10
− ϕ
6
sin x
11
cos x
10
,
Ψ
k
= x
k
− x
∗
k
,k=8, 9,...,12.
x
∗
k
T
k
˙
Ψ
k
(t)+Ψ
k
=0,k=8, 9,...,12,
T
k
ϕ
i
x
k
T
m
,T
k
V,x
∗
k
ϕ
i
u(x) x =[x
n
]
T
n =1, 2,...,12
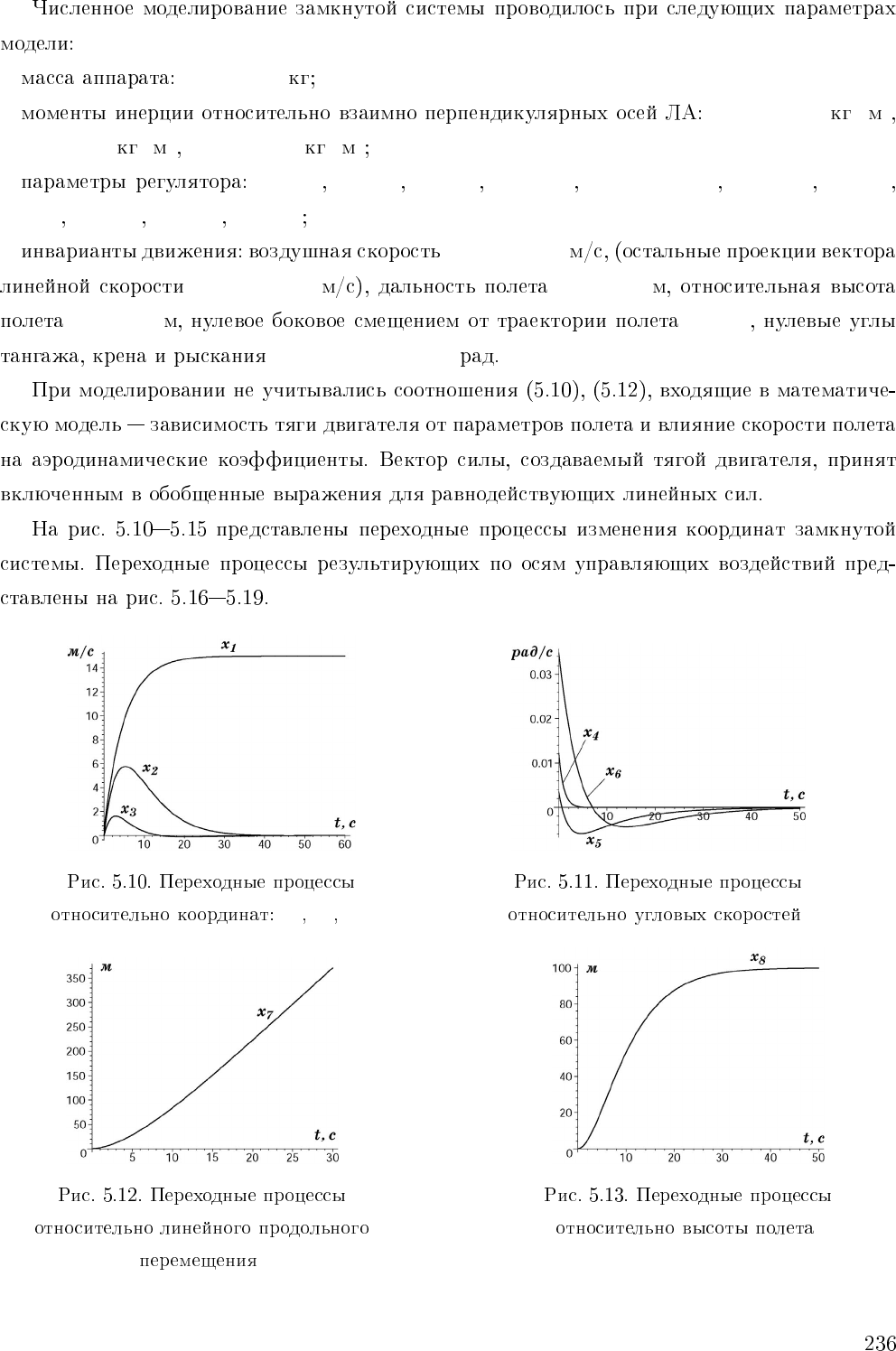
• m = 25000
• I
x
= 48000 ·
2
I
y
= 150000 ·
2
I
z
= 116000 ·
2
• T
1
=5 T
2
=6 T
3
=5 T
4
=3,5 T
5
= T
6
=10 T
7
=0,5 T
8
=5
T
9
=2 T
10
=5 T
11
=1 T
12
=2
• x
∗
1
= V =15
x
∗
2
= x
∗
3
=0 x
∗
7
> 300
x
∗
8
= 100 x
∗
9
=0
x
∗
10
= x
∗
11
= x
∗
12
=0
x
1
x
2
x
3
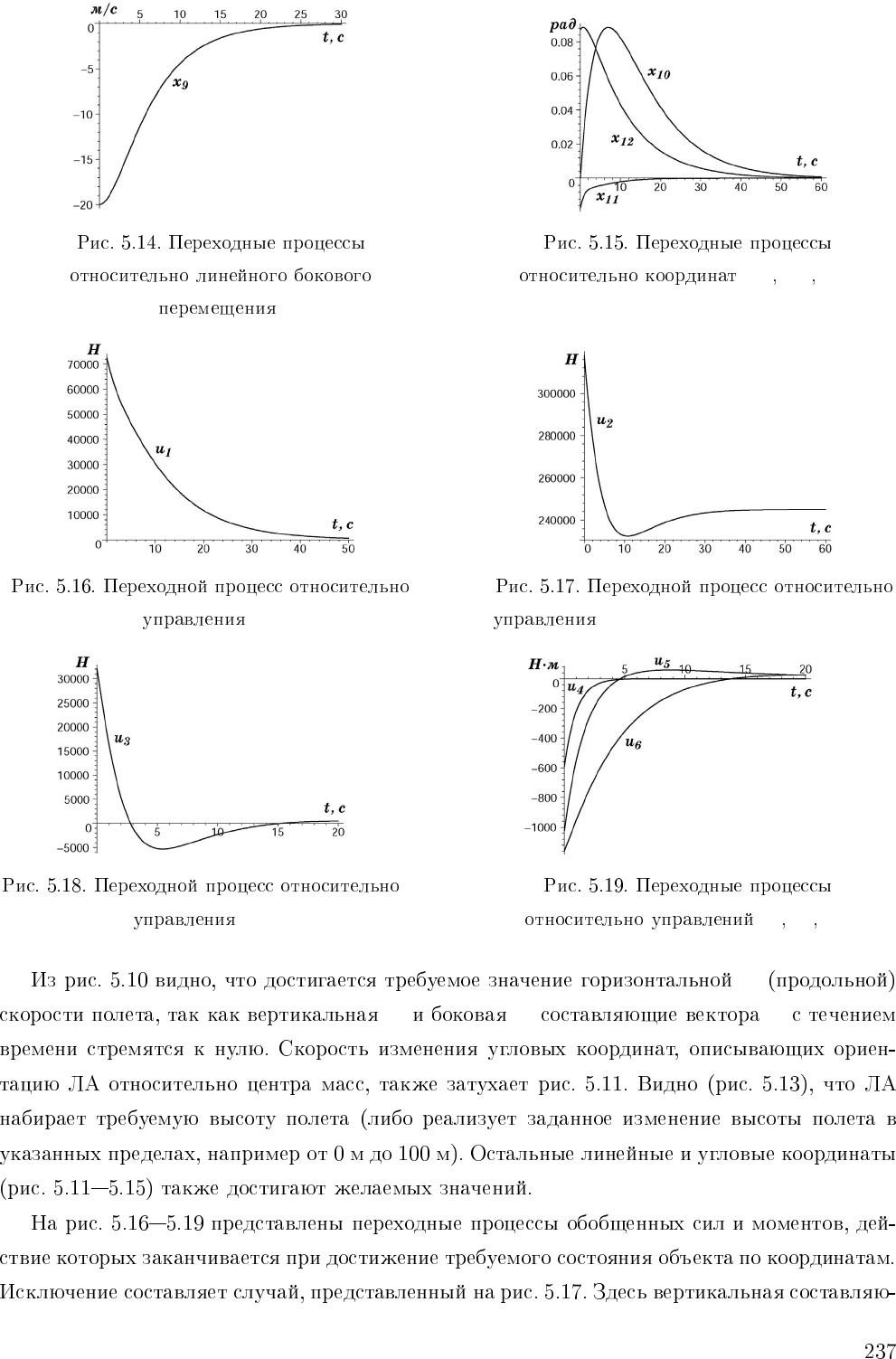
x
10
x
11
x
12
u
1
u
2
u
3
u
4
u
5
u
6
x
1
x
2
x
3
V
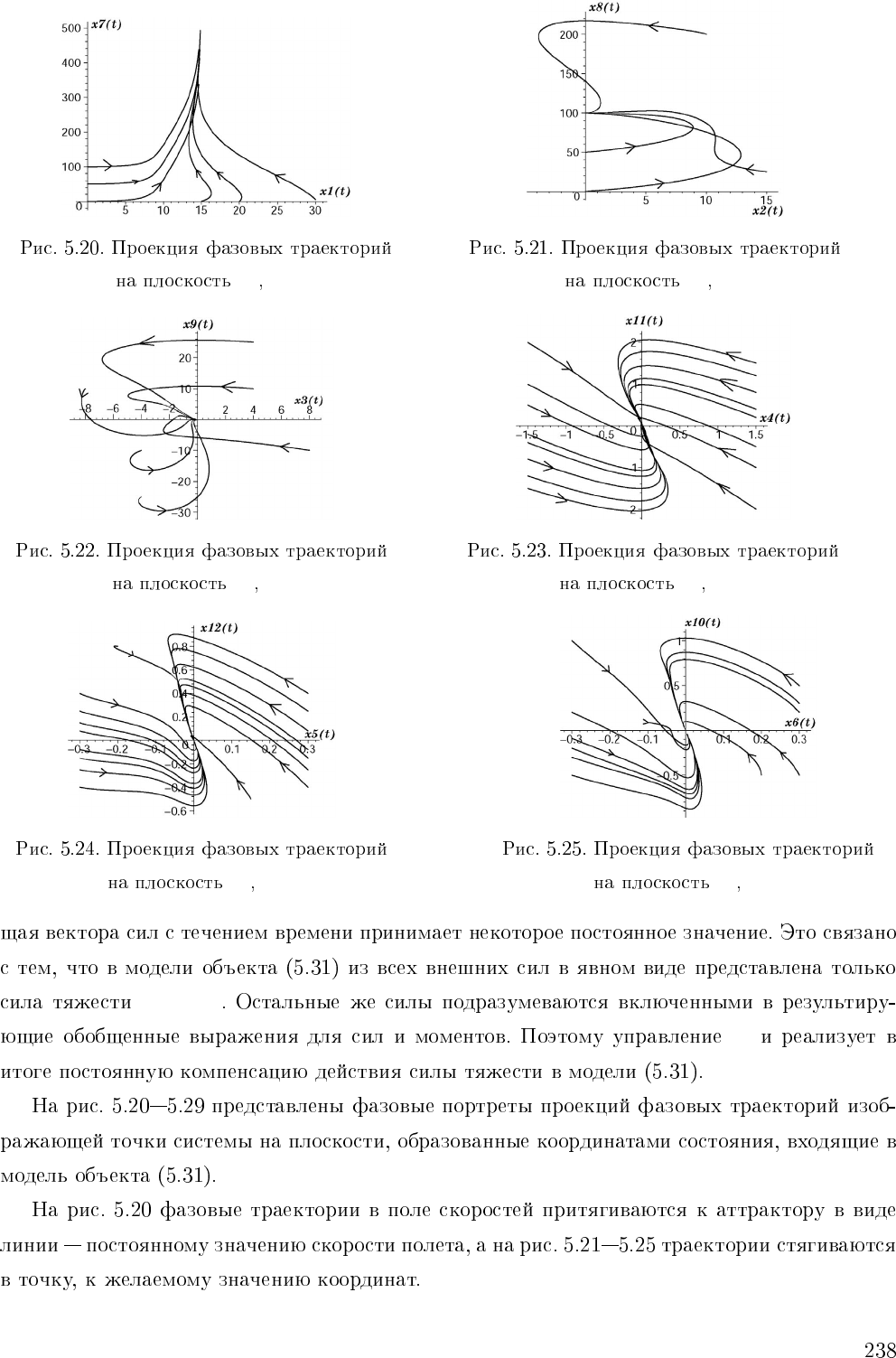
x
1
x
7
x
2
x
8
x
3
x
9
x
4
x
11
x
5
x
12
x
6
x
10
G = mg
u
2
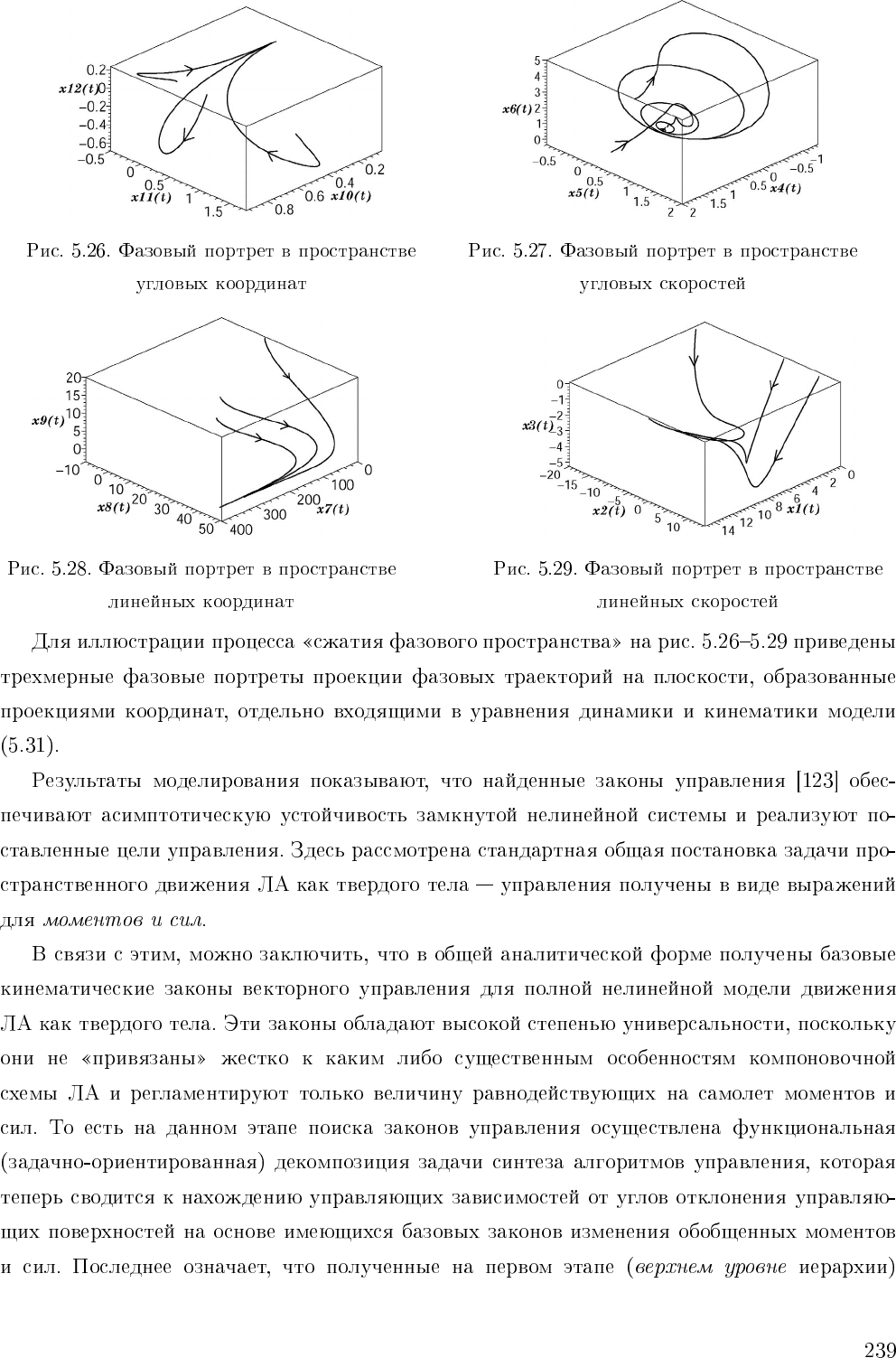

δ
F =
&
c
z
c
y
c
z
'
, M =
&
m
z
m
y
m
z
'
δ δ
P
δ
δ
1
=
−k
δ
1
1
+ k
δ
1
2
u
3
− k
δ
1
3
u
4
− k
δ
1
4
u
5
−k
δ
1
6
+ k
δ
1
7
u
3
− k
δ
1
8
u
4
;
δ
2
= −k
δ
2
1
u
4
+ k
δ
2
2
u
3
− k
δ
2
3
;
δ
3
=
k
δ
3
1
u
6
− k
δ
3
2
u
2
− k
δ
3
3
u
4
+
k
δ
3
3
u
2
− k
δ
3
5
u
6
− k
δ
3
7
u
3
−
− k
δ
3
8
u
2
+ k
δ
3
9
u
5
+ k
δ
3
10
u
6
+ k
δ
3
11
1
−k
δ
3
12
− k
δ
3
13
u
4
+ k
δ
3
14
u
3
;
δ
4
=
k
δ
4
4
− k
δ
4
2
u
2
+ k
δ
4
3
u
6
− k
δ
4
4
u
1
u
4
+
− k
δ
4
5
+ k
δ
4
6
u
2
− k
δ
4
7
u
6
+
+ k
δ
4
8
u
1
u
3
+ k
δ
4
9
+ k
δ
4
10
u
6
− k
δ
4
11
u
2
+ k
δ
4
12
u
5
1
k
δ
4
13
+ k
δ
4
14
u
3
− k
δ
4
15
u
4
;
