Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.


b
1
b
2
,b
3
...b
m
I
2
=
b
1
(b
2
,b
3
...b
m
) −
x
3
cos x
6
− x
1
sin x
6
+ z
1
1
x
5
x
1
cos x
6
+ x
3
sin x
6
− z
1
2
x
5
2
+
+
m
j=2
b
j
−
x
3
cos x
6
− x
1
sin x
6
+ z
j
1
x
5
x
1
cos x
6
+ x
3
sin x
6
− z
j
2
x
5
2
−→ min .
b
1
(b
2
,b
3
..b
m
)
b
1
(b
j
)=χ
(b
j
− χ
1
)(b
j
− χ
2
)
(b
j
− χ
3
)(b
j
− χ
4
)
,b
j
∈{b
2
,b
3
..b
m
},
χ, χ
1
..χ
4
∂I
2
∂b
j
=0
b
j
˙
B(t)=−
∂
2
I
2
∂B∂B
T
−1
∂
T
I
2
∂B
.
∂
2
I
2
∂B∂B
T
∂
T
I
2
∂B
I
2
(B) B =[b
2
b
3
...b
m
]
T
∂
2
I
2
∂B∂B
T
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂
2
I
2
∂b
2
2
∂
2
I
2
∂b
2
∂b
3
···
∂
2
I
2
∂b
2
∂b
m
∂
2
I
2
∂b
2
∂b
3
∂
2
I
2
∂b
2
3
···
∂
2
I
2
∂b
3
∂b
m
··· ··· ··· ···
∂
2
I
2
∂b
2
∂b
m
∂
2
I
2
∂b
3
∂b
m
···
∂
2
I
2
∂b
2
m
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
∂
T
I
2
∂B
=
∂I
2
∂b
2
∂I
2
∂b
3
···
∂I
2
∂b
m
∂I
2
∂b
j
=0,b
j
∈{b
2
,b
3
..b
m
}
sign
∂
2
I
2
∂b
2
j
=
⎧
⎨
⎩
1, min;
−1, max .

f
j
pr
I
1
b
j
I
2
F
1
=
1
3
ν
j=1
1
1+b
2
j
p
(j)
L
(j)
m
m
(j)
r
j
L
(j)
r
ψ
(j)
const
ϕ
(j)
2
;
F
2
=
1
3
ν
j=1
b
j
1+b
2
j
p
(j)
L
(j)
m
m
(j)
r
j
L
(j)
r
ψ
(j)
const
ϕ
(j)
2
;
M =
1
3
ν
j=1
z
j
1
− z
j
2
b
j
1+b
2
j
p
(j)
L
(j)
m
m
(j)
r
j
L
(j)
r
ψ
(j)
const
ϕ
(j)
2
,
ϕ
(1)
2
,ϕ
(2)
2
,b
1
I
1
I
1
= q
1
ϕ
(1)
2
ϕ
(3)
2
...ϕ
(m)
2
2
+ q
2
ϕ
(2)
2
ϕ
(3)
2
...ϕ
(m)
2
2
+
+
m
j=3
q
j
ϕ
(j)
2
2
−→ min .
ϕ
(3)
2
,ϕ
(4)
2
,ϕ
(m)
2
∂I
1
∂ϕ
(3)
2
=0;
∂I
1
∂ϕ
(4)
2
=0;...;
∂I
1
∂ϕ
(m)
2
=0.
ϕ
(3)
2
,ϕ
(4)
2
,...ϕ
(m)
2
b
1
I
2
˙
B(t)=−
∂
2
I
2
∂B∂B
T
−1
∂
T
I
2
∂B
.

f(x, y)
{x, y} f(x, y)
f(x, y)=C
{0}
+
n
i=1
C
{x}
i
x
i
+
n
i=1
C
{y}
i
y
i
+
n
i=1
n
k=1
C
{xy}
i,k
x
i
y
k
,
C
{0}
,C
{x}
i
,C
{y}
i
,C
{xy}
i,k
,i,k =1..n
{x
1
,y
1
}, {x
2
,y
2
}...,
C
{0}
=1
B =(P
T
P)
−1
P
T
E,
P =
&
P
1
P
2
P
3
'
P
1
=
$
$
$
$
$
$
$
$
$
$
$
x
1
y
1
x
1
y
1
... x
i
1
x
2
y
2
x
2
y
2
... x
i
2
x
ζ
y
ζ
x
ζ
y
ζ
... x
i
ζ
$
$
$
$
$
$
$
$
$
$
$
; P
2
=
$
$
$
$
$
$
$
$
$
$
$
y
i
1
x
i
1
y
1
... x
i
1
y
i−1
1
y
i
2
x
i
2
y
2
... x
i
2
y
i−1
2
y
i
ζ
x
i
ζ
y
ζ
... x
i
ζ
y
i−1
ζ
$
$
$
$
$
$
$
$
$
$
$
;
P
3
=
$
$
$
$
$
$
$
$
$
$
$
x
1
y
i
1
... x
i
1
y
i
1
... x
n
1
y
n
1
x
2
y
i
2
... x
i
2
y
i
2
... x
n
2
y
n
2
x
ζ
y
i
ζ
... x
i
ζ
y
i
ζ
... x
n
ζ
y
n
ζ
$
$
$
$
$
$
$
$
$
$
$
;
B =
&
C
{x}
1
C
{y}
1
C
{xy}
1,1
...C
{x}
i
C
{y}
i
C
{xy}
i,1
...C
{xy}
i,i−1
C
{xy}
1,i−1
...C
{xy}
i,i
...C
{xy}
n,n
'
T
;

ζ =2n + n
2
dim E =1× 2n + n
2
n =1 {x
1
,y
1
}, {x
2
,y
2
}, {x
3
,y
3
}
⎡
⎢
⎢
⎣
C
{x}
1
C
{y}
1
C
{xy}
1,1
⎤
⎥
⎥
⎦
=
⎛
⎜
⎜
⎝
⎡
⎢
⎢
⎣
x
1
x
2
x
3
y
1
y
2
y
3
x
1
y
1
x
2
y
2
x
3
y
3
⎤
⎥
⎥
⎦
⎡
⎢
⎢
⎣
x
1
y
1
x
1
y
1
x
2
y
2
x
2
y
2
x
3
y
3
x
3
y
3
⎤
⎥
⎥
⎦
⎞
⎟
⎟
⎠
−1
⎡
⎢
⎢
⎣
x
1
x
2
x
3
y
1
y
2
y
3
x
1
y
1
x
2
y
2
x
3
y
3
⎤
⎥
⎥
⎦
⎡
⎢
⎢
⎣
1
1
1
⎤
⎥
⎥
⎦
C
{x}
1
=
−y
3
x
1
y
1
+ y
2
x
1
y
1
+ y
1
x
3
y
3
+ x
2
y
2
y
3
− y
2
x
3
y
3
− y
1
x
2
y
2
y
1
x
2
y
2
x
3
+ y
1
x
2
y
3
x
1
− y
1
y
2
x
1
x
3
− x
2
y
2
y
3
x
1
− y
1
x
2
x
3
y
3
+ y
2
x
1
x
3
y
3
;
C
{y}
1
y = y
−x
2
y
2
x
3
+ x
2
x
3
y
3
− x
1
x
3
y
3
+ x
2
y
2
x
1
+ y
1
x
1
x
3
− y
1
x
2
x
1
y
1
x
2
y
2
x
3
+ y
1
x
2
y
3
x
1
− y
1
y
2
x
1
x
3
− x
2
y
2
y
3
x
1
− y
1
x
2
x
3
y
3
+ y
2
x
1
x
3
y
3
;
C
{xy}
1,1
y = y
y
1
x
3
− y
2
x
3
− y
3
x
1
− y
1
x
2
+ x
2
y
3
+ y
2
x
1
y
1
y
2
x
1
x
3
− y
1
x
2
y
2
x
3
− y
1
x
2
y
3
x
1
+ x
2
y
2
y
3
x
1
+ y
1
x
2
x
3
y
3
− y
2
x
1
x
3
y
3
,
{x
1
,y
1
}, {x
2
,y
2
}, {x
3
,y
3
}
P
ψ
1
= C
{0}
+
n
i=1
C
{x}
i
x
i
1
+
n
i=1
C
{y}
i
x
i
3
+
n
i=1
n
k=1
C
{xy}
i,k
x
i
1
x
k
3
,
x
1
= x, x
3
= y
ψ
1
=0
ψ
2
= x
2
2
+ x
2
4
− V
2
k
.
V
k
ψ
3
=
ϑ(x
5
) − sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
+
+ ζ
⎛
⎝
π
2
−
ϑ(x
5
) − sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
2
⎞
⎠
x
6
.

T
1
¨
ψ
1
(t)+T
2
˙
ψ
1
(t)+ψ
1
=0;
T
3
˙
ψ
2
(t)+ψ
2
=0;
T
4
˙
ψ
3
(t)+ψ
3
=0.
F
1
(x),F
2
(x),M(x)
f(x
1
,x
3
) V
k
F
1
(x)=
m
0
(T
1
ν
14
ν
11
(T
4
ν
15
+ ψ
3
)+2ν
10
T
3
T
4
P
4
ν
17
(π
2
− ν
2
14
)))
2T
3
T
1
T
4
P
4
(ν
2
14
− π
2
)(ν
16
ν
11
+ ν
17
ν
12
)
;
F
2
(x)=
m
0
(T
1
ν
12
(T
4
P
4
(1 − 2ζν
14
x
6
)+ψ
3
)+T
4
ζ(π
2
− ν
14
)(T
3
P
4
ν
16
ν
10
− T
1
ν
12
))
ζ2T
3
T
1
T
4
P
4
(π
2
− ν
2
14
)(ν
16
ν
11
+ ν
17
ν
12
)
;
M(x)=
m
0
⎛
⎜
⎝
2T
3
T
4
ν
16
sign(x
4
)
x
2
2
+ x
2
4
ν
12
− x
2
2
sin x
5
−
− sign(x
4
)x
2
4
ζν
14
x
6
cos x
5
+ T
1
T
3
ν
12
ν
17
(T
4
+ ψ
3
) − T
1
ν
17
ν
15
ν
10
x
2
2
+ x
2
4
⎞
⎟
⎠
ζ2T
3
T
1
T
4
P
4
(π
2
− ν
2
14
)(ν
16
ν
11
+ ν
17
ν
12
)
,
ν
i,k
= C
{xy}
i,k
x
i
1
x
k
3
i =1...m k =1...m ν
1
=
m
4
i=1
C
{x}
i
x
i−1
1
i ν
2
=
m
4
k=1
m
4
i=1
ν
i,k
ix
−1
1
ν
3
=
m
4
k=1
C
{y}
k
x
k−1
3
k ν
4
=
m
4
k=1
m
4
i=1
ν
i,k
x
−1
3
k ν
5
=
m
4
i=1
C
{x}
i
x
i−2
1
i(i − 1) ν
6
=
m
4
k=1
m
4
i=1
ν
i,k
x
−2
1
i(i − 1)
ν
7
=
m
4
k=1
m
4
i=1
ν
i,k
x
−1
1
x
−1
3
ik ν
8
=
m
4
k=1
C
{y}
k
x
k−2
3
k(k − 1) ν
9
=
m
4
k=1
m
4
i=1
ν
i,k
x
−2
3
k(k − 1)
ν
10
= T
1
(((ν
5
+ν
6
)x
2
+ν
7
x
4
)x
1
+(ν
7
x
2
+(ν
8
+ν
9
)x
4
)x
4
)+T
2
ν
18
+ψ
1
ν
11
=(ν
3
+ ν
4
)cosx
5
− (ν
1
+ ν
2
)sinx
5
ν
12
=(ν
1
+ ν
2
)cosx
5
+(ν
3
+ ν
4
)sinx
5
ν
13
= arccos
x
2
x
2
2
+ x
2
4
ν
14
= ϑ(x
5
) − sign(x
4
)ν
13
ν
15
= ζ − (1 − 2ζν
14
x
6
)x
6
ν
16
= x
2
cos x
5
+ x
4
sin x
5
ν
17
= x
4
cos x
5
− x
2
sin x
5
ν
18
=(ν
1
+ν
2
)x
2
+(ν
3
+ν
4
)x
4

ψ
1
= P
1
(x
1
− x
0
1
)+P
2
(x
3
− x
0
3
);
ψ
2
= P
3
(x
1
− x
0
1
)+P
4
(x
3
− x
0
3
);
ψ
3
=ϑ(x
5
) − sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
+
+ ζ
⎛
⎝
π
2
−
ϑ(x
5
) − sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
2
⎞
⎠
x
6
.
ψ
1
,ψ
2
,ψ
3
T
1
¨
ψ
1
(t)+T
2
˙
ψ
1
(t)+ψ
1
=0;
T
3
¨
ψ
2
(t)+T
4
˙
ψ
2
(t)+ψ
2
=0;
T
5
˙
ψ
3
(t)+ψ
3
=0.
F
1
(x),F
2
(x),M(x) {x
0
1
,x
0
3
}
F
1
(x)=
ν
6
ν
3
ν
5
(sin(x
5
)P
3
+cos(x
5
)P
4
)P
1
+
ν
7
ν
3
P
4
−
−
T
2
x
4
+ x
3
− x
0
3
T
1
m
0
sin(x
5
) −
T
4
x
2
+ x
1
− x
0
1
T
3
m
0
cos(x
5
);
F
2
(x)=
cos(x
5
)sin(x
5
)
ν
3
ν
5
(P
3
ν
6
− P
4
ν
7
)P
1
2
+
T
4
x
2
+ x
1
− x
0
1
T
3
m
0
sin(x
5
)+
+
ν
7
ν
3
ν
5
P
4
P
2
+
ν
6
ν
3
ν
5
P
4
P
1
+
ν
6
ν
5
P
1
cos
2
(x
5
) −
T
2
x
4
+ x
3
− x
0
3
T
1
m
0
cos(x
5
)+
+
ν
7
ν
3
sin(x
5
)P
4
P
2
+
ν
6
ν
3
ν
5
sin(x
5
)+
ν
7
ν
3
cos(x
5
)
P
4
P
1
;

M(x)=J
0
((T
3
− T
1
) P
1
P
3
x
1
− (P
3
P
2
T
1
− (ν
3
+ P
3
P
2
) T
3
) x
4
) x
0
1
ν
2
T
1
T
3
(x
2
2
+ x
4
2
) ν
3
ν
4
−
− J
0
(((ν
3
+ P
3
P
2
) T
1
− P
3
P
2
T
3
) x
2
+(T
1
− T
3
) P
2
P
4
x
4
) x
0
3
ν
2
T
1
T
3
(x
2
2
+ x
4
2
) ν
3
ν
4
−
− J
0
(sign(x
4
)ν
1
− ϑ(x
5
)) 2T
5
x
6
2
− ν
8
x
6
+ ν
1
ν
2
+ ϑ(x
5
)ζ
T
3
(x
2
2
+ x
4
2
) T
5
ν
3
ν
4
+
+ J
0
x
2
ν
2
(+P
1
P
3
(T
3
− T
1
) x
1
+(ν
3
+ P
3
P
2
) T
1
x
3
)
T
1
T
3
(x
2
2
+ x
4
2
) ν
3
ν
4
+
+ J
0
(2T
5
(sign(x
4
)ν
1
−ϑ(x
5
)) x
6
2
+ν
8
x
6
+ν
1
ν
2
+ϑ(x
5
)ζ) x
4
2
(x
2
2
+ x
4
2
) T
5
ν
4
+
+ J
0
((ν
3
+ P
3
P
2
) T
3
x
1
+(T
3
− T
1
) x
3
P
2
P
4
) x
4
ν
2
T
1
T
3
(x
2
2
+ x
4
2
) ν
3
ν
4
−
− J
0
P
3
P
1
T
5
ν
2
(T
2
T
3
−T
1
T
4
)−x
2
2
T
3
+P
3
P
2
T
5
(T
1
x
4
ν
2
−T
3
x
3
)
T
1
T
3
(x
2
2
+ x
4
2
) T
5
ν
3
ν
4
+
+ J
0
ν
2
x
4
(T
1
T
4
− T
2
T
3
)((2P
2
P
3
− ν
3
)x
2
− P
4
P
2
x
4
)
T
1
T
3
(x
2
2
+ x
4
2
) ν
3
ν
4
,
ν
1
= arccos
x
2
x
2
2
+ x
2
4
ν
2
=2sign(x
4
)x
6
− sign(x
4
)ζ − ϑ(x
5
) ν
3
= P
4
P
1
− P
2
P
3
ν
4
= π
2
− ϑ(x
5
)
2
+2sign(x
4
)ϑ(x
5
)ν
1
ν
5
= P
1
sin(x
5
) − P
2
cos(x
5
) ν
8
= ϑ(x
5
)
2
− T
5
ζ − π
2
ν
6
=
m
0
(x
2
(T
4
T
1
− T
2
T
3
) − (T
1
− T
3
)(x
0
1
− x
1
))
T
3
T
1
ν
7
=
m
0
(x
4
(T
4
T
1
− T
2
T
3
) − (T
1
− T
3
)(x
0
3
− x
3
))
T
3
T
1
ϕ
1
,ϕ
2
˙x
1
(t)=ϕ
1
;
˙x
3
(t)=ϕ
2
,
x
1
,x
3
T
1
˙
ψ
1
(t)+ψ
1
=0;
T
2
˙
ψ
2
(t)+ψ
2
=0.
ϕ
1
(x),ϕ
2
(x)
ϕ
1
(x)=
P
2
(P
4
(x
3
−x
0
3
)+P
3
(x
1
−x
0
1
))
T
2
(P
1
P
4
− P
2
P
3
)
−
P
4
(P
2
(x
3
−x
0
3
)+P
1
(x
1
−x
0
1
))
T
1
(P
1
P
4
− P
2
P
3
)
;
ϕ
2
(x)=
P
3
(P
2
(x
3
−x
0
3
)+P
1
(x
1
−x
0
1
))
T
2
(P
1
P
4
− P
2
P
3
)
−
P
1
(P
4
(x
3
−x
0
3
)+P
3
(x
1
−x
0
1
))
T
1
(P
1
P
4
− P
2
P
3
)
.

ϕ
1
(x),ϕ
2
(x)
x
2
,x
4
F
1
(x) F
2
(x)
ψ
3
= x
2
−
ϕ
1
V
k
ϕ
2
1
+ ϕ
2
2
=0;
ψ
4
= x
4
−
ϕ
2
V
k
ϕ
2
1
+ ϕ
2
2
=0.
ψ
3
=0 ψ
4
=0
x
2
2ψ
3
+ x
2
4ψ
4
= V
k
,
V
k
V
k
V
k
= V
k
tanh
ξ
(x
1
− x
0
1
)
2
+(x
3
− x
0
3
)
2
,
V
k
ξ
ψ
5
=ϑ(x
5
) − sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
+
+ ζ
⎛
⎝
π
2
−
ϑ(x
5
) − sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
2
⎞
⎠
x
6
.
T
3
˙
ψ
3
(t)+ψ
3
=0;
T
4
˙
ψ
4
(t)+ψ
4
=0;
T
5
˙
ψ
5
(t)+ψ
5
=0.
F
1
(x),F
2
(x),M(x)
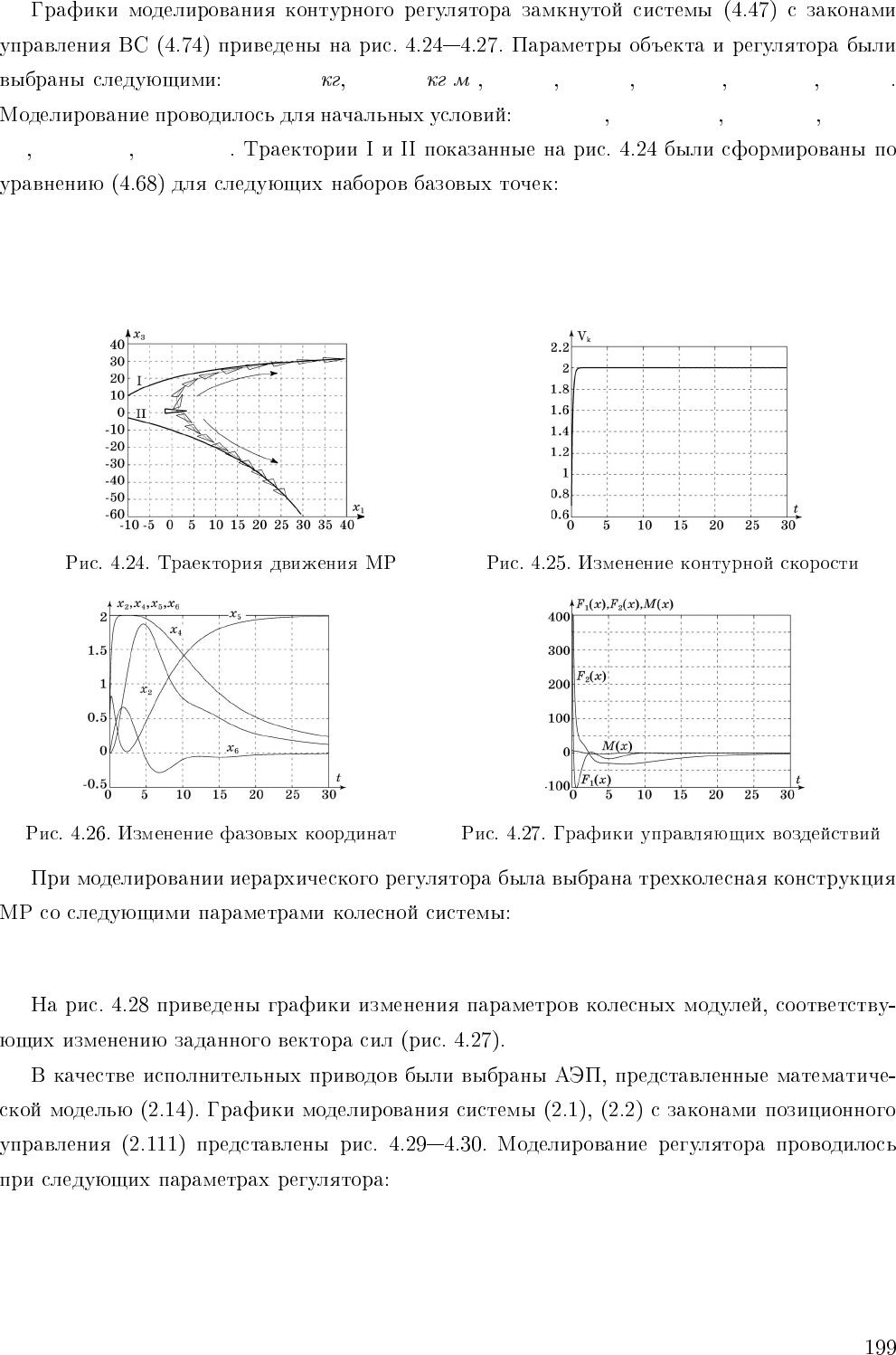
m
0
= 150 J
0
=72 ·
2
T
1
=6 T
2
=6 T
3
=0.5 T
4
=0.5 V
k
=2
x
1
(0) = 1 x
2
(0) = 0.5 x
3
(0) = 1 x
4
(0) =
0.5
x
5
(0) = 0 x
6
(0) = 0
I: {x
{1}
1
=0,x
{1}
3
=20}, {x
{2}
1
=10,x
{2}
3
=25}, {x
{3}
1
=30,x
{3}
3
=30};
II : {x
{1}
1
=0,x
{1}
3
= −10}, {x
{2}
1
=10,x
{2}
3
= −20}, {x
{3}
1
=20,x
{3}
3
= −35}.
z
1
1
=5,z
1
2
=3,z
2
1
=5,z
2
2
= −3,z
3
1
= −5,z
3
2
=0.
ψ
r0
=0, 4,T
1
=0, 5,T
2
=0, 5,T
3
=0, 6,T
4
=0, 2,
β
11
=1,β
12
=2,β
21
=3,β
22
=4,γ
1
=10,γ
2
=2.
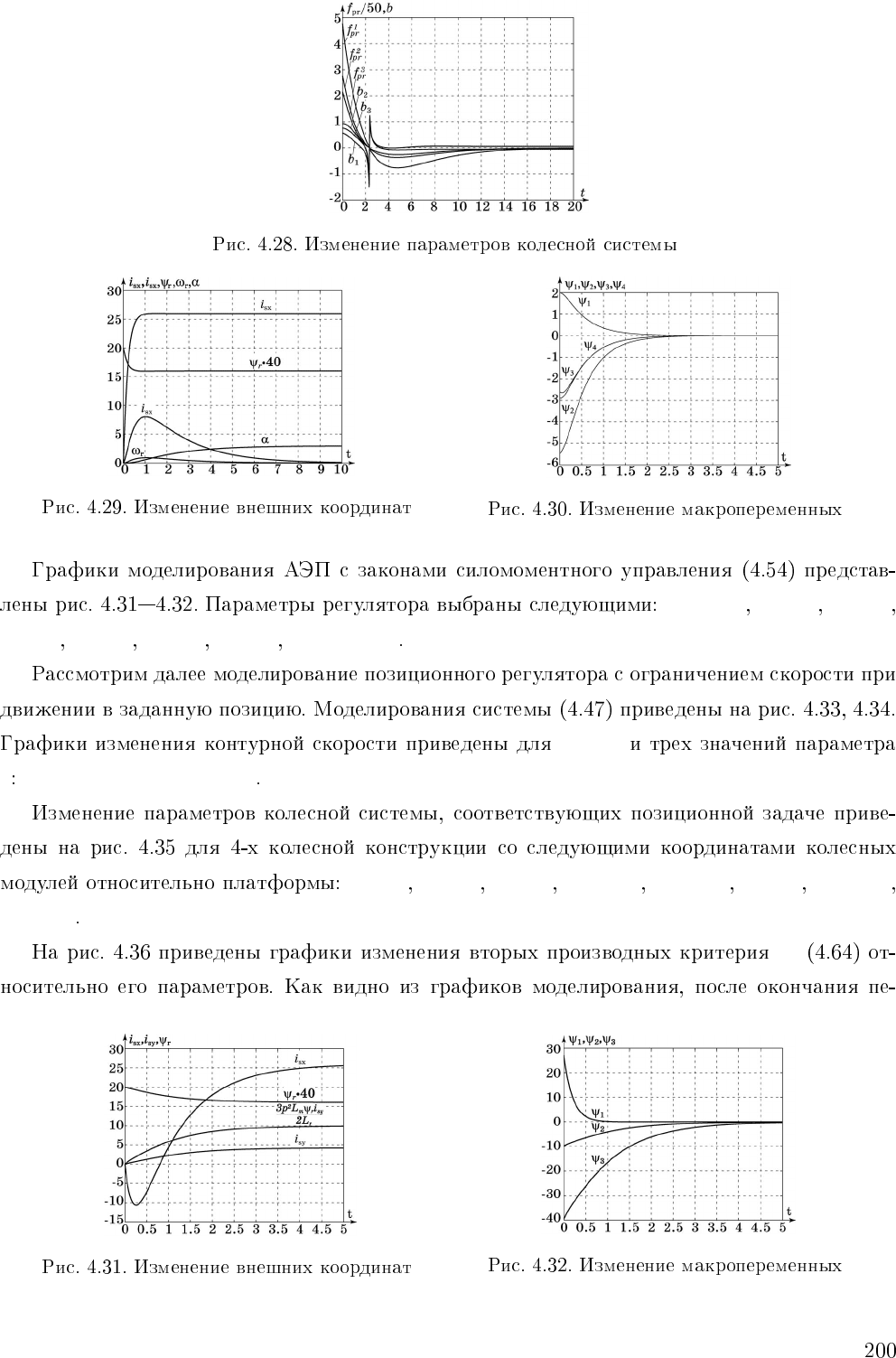
T
1
=0, 2 T
2
=1 T
3
=1
β
1
=1 β
2
=2 β
3
=4 β
4
=3 ψ
const
=0, 4
V
k
=2
ξ {ξ =1,ξ =0.1,ξ =0.01}
z
1
1
=5 z
1
2
=3 z
2
1
=5 z
2
2
= −3 z
3
1
= −5 z
3
2
=3 z
4
1
= −5
z
4
2
= −3
I
2
