Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.

[b
2
b
3
...b
m
]
I
2
θ
r
=const

M=const ψ
r
=const
•
•
•
•
•
f(x, y)=C
{0}
+
n
i=1
C
{x}
i
x
i
+
n
i=1
C
{y}
i
y
i
+
n
i=1
n
k=1
C
{xy}
i,k
x
i
y
k
,
x
{prep}
1
=
3.8,x
{prep}
3
=4.1 L =1.3
x
1
= {2.73.64.24.85.4};
x
3
= {2.22.93.34.04.8}.
C
{0}
=1,C
{x}
1
= −0.06,C
{y}
1
=0.29,C
{xy}
11
= −0.07,
C
{x}
2
=0.05,C
{y}
2
=0.05.

˙y
0
= V
0
,m
0
˙
V
0
=0,
˙α
0
= ω
0
,J
0
˙ω
0
=0,
y
0
= {y
0
1
,y
0
2
} α
0
V
0
∈
2
ω
0
m
0
J
0
y
0
V
0
x
1
,x
3
x
1
x
3
=
cos θ −sin θ
sin θ cos θ
x
1
x
3
.

θ C
0
D θ
C
0
C
0
C
0
x
{pr}
1
,x
{pr}
3
C
0
x
{pr}
1
cos θ − x
{pr}
3
sin θ, x
{pr}
1
sin θ + x
{pr}
3
cos θ
x
{pr}
1
−x
{pr}
1
cos θ+x
{pr}
3
sin θ
2
+
x
{pr}
3
−x
{pr}
1
sin θ−x
{pr}
3
cos θ
2
= D.
θ
θ
1
= arctan
D
4µ − D
2
D
2
− 2µ
,θ
2
= −arctan
D
4µ − D
2
D
2
− 2µ
,
θ = ρ arctan
D
4µ − D
2
D
2
− 2µ
,
µ =
x
{pr}
1
2
+
x
{pr}
3
2
ρ = ±1
x
1
,x
3
γ
1
x
1
,x
3
V
γ
2
[0; 2π]
γ
1
=sign
x
{pr}
3
−x
{MP}
3
arccos
⎛
⎜
⎜
⎝
x
{pr}
1
−x
{MP}
1
x
{pr}
1
−x
{MP}
1
2
+
x
{pr}
3
−x
{MP}
3
2
⎞
⎟
⎟
⎠
−
− π
sign
x
{pr}
3
− x
{MP}
3
− 1
;
γ
2
=sign(x
4
) arccos
x
2
x
2
2
+ x
2
4
− π(sign(x
4
) − 1),
x
2
,x
4

γ
2
− γ
1
−
π
2
<γ
2
− γ
1
<
π
2
ρ
ρ =
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
1, (γ
2
− γ
1
) ∈
)
0;
π
2
*
∨ (γ
2
− γ
1
) ∈
+
−2π; −
3π
2
,
;
−1, (γ
2
− γ
1
) ∈
)
−
π
2
;0
*
∨ (γ
2
− γ
1
) ∈
+
3π
2
;2π
,
;
0, |γ
2
− γ
1
|∈
+
π
2
;
3π
2
,
,
∨
ρ
D =(D
0
+r)
1−tanh
ξ
x
{pr}
1
−x
{MP}
1
2
+
x
{pr}
3
−x
{MP}
3
2
,
ξ =const D
0
r
D → 0 D → (D
0
+ r)
+
x
{pr}
1
− x
{MP}
1
2
+
x
{pr}
3
− x
{MP}
3
2
→∞
,
⇒
⇒{D → 0}⇒{θ → 0}⇒
)
x
1
,x
3
→ (x
1
,x
3
)
*
,
(x
1
,x
3
)
x
1
,x
3
•
⎧
⎨
⎩
ψ
1
= P
1
(x
1
−x
0
1
)+P
2
(x
3
−x
0
3
);
ψ
2
= P
3
(x
1
−x
0
1
)+P
4
(x
3
−x
0
3
).
=⇒
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎩
ψ
1
=P
1
(x
1
cos θ+x
3
sin θ−x
0
1
)+
+P
2
(−x
1
sin θ+x
3
cos θ−x
0
3
);
ψ
2
=P
3
(x
1
cos θ+x
3
sin θ−x
0
1
)+
+P
4
(−x
1
sin θ+x
3
cos θ−x
0
3
).
•
ψ
1
= f(x
1
,x
3
)=⇒ ψ
1
= f(x
1
cos θ + x
3
sin θ, −x
1
sin θ + x
3
cos θ).
˙x
{pr}
1
(t)=x
{pr}
2
;
˙x
{pr}
3
(t)=x
{pr}
4
.
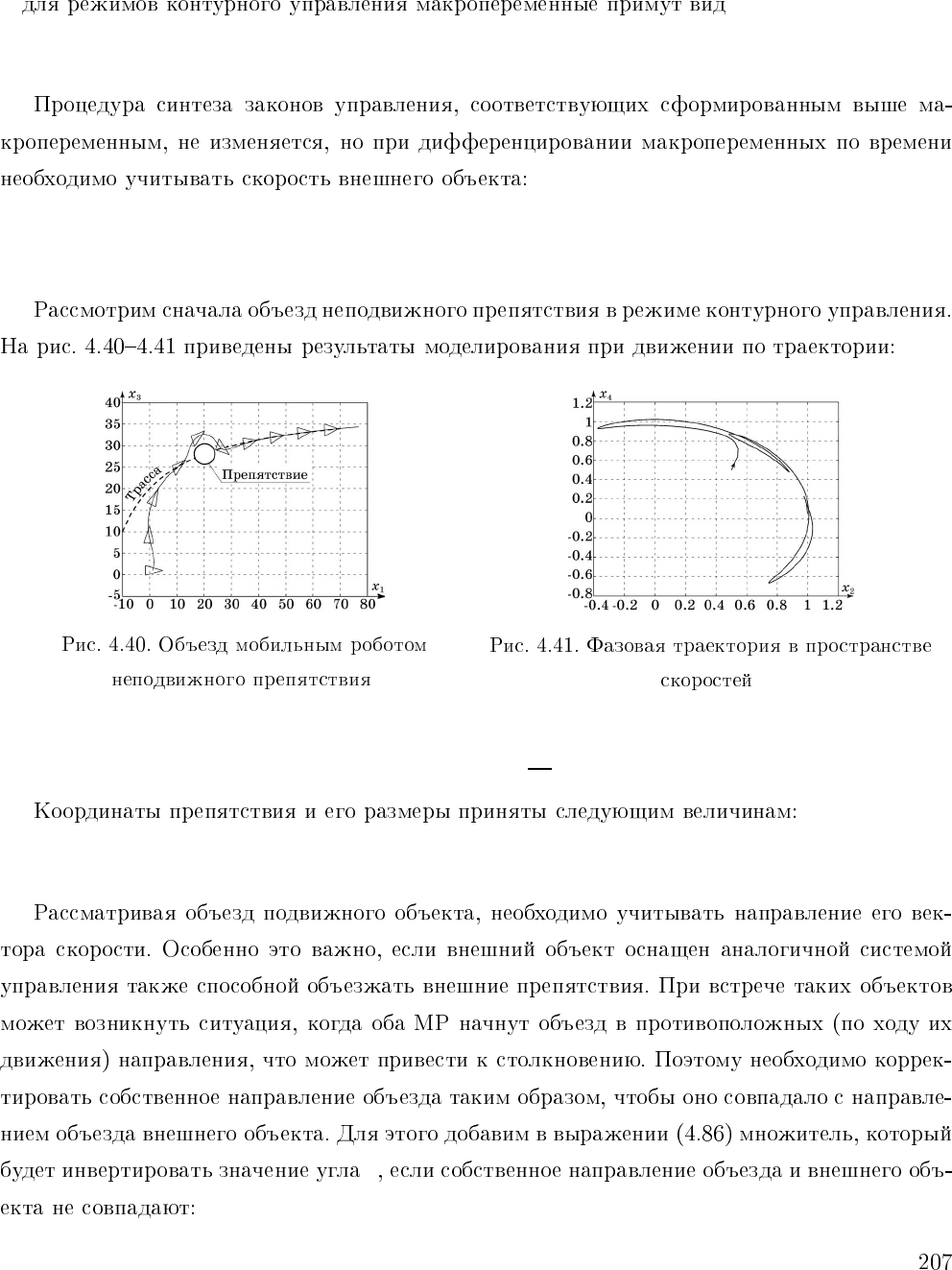
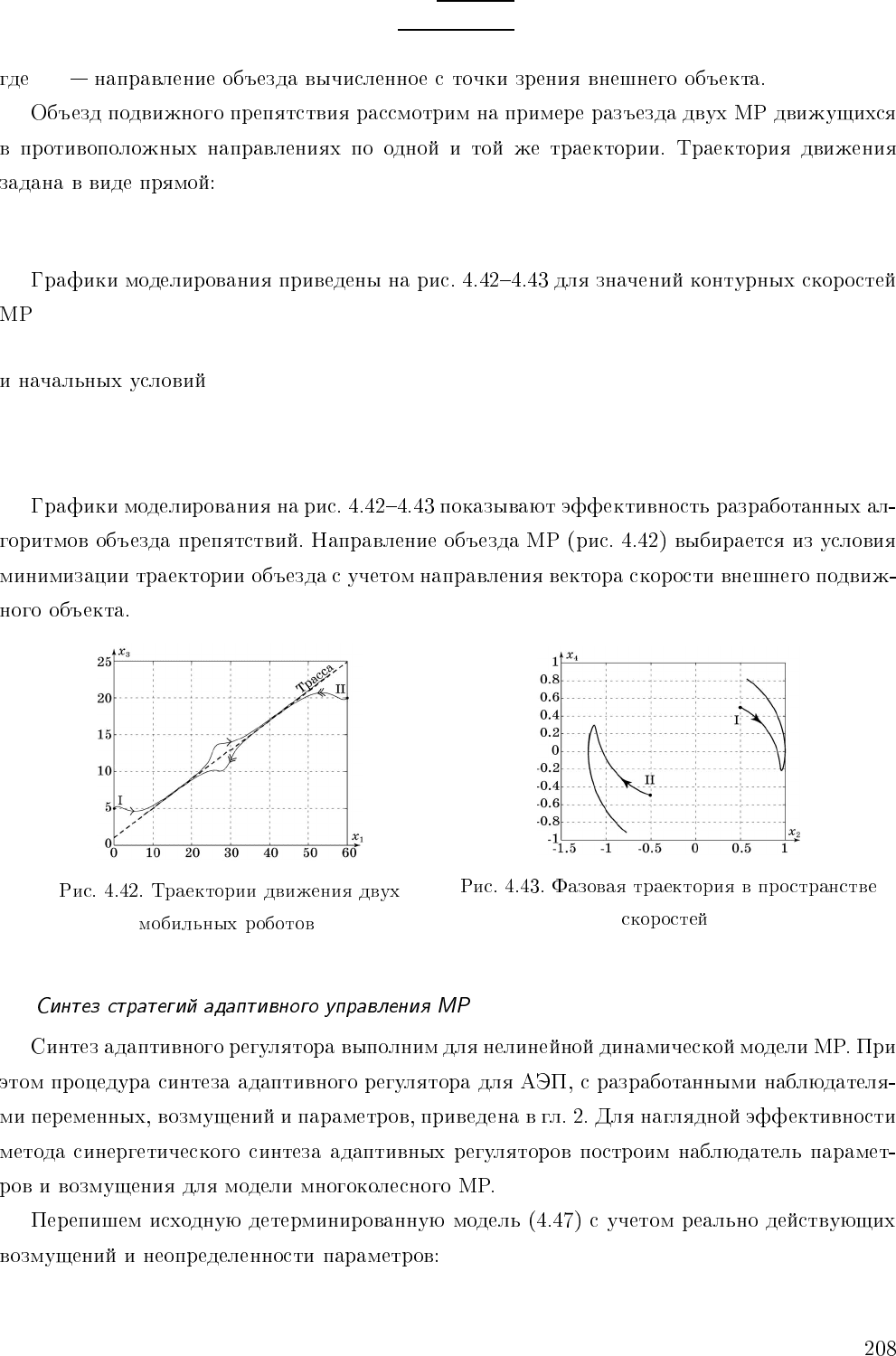
f(x
1
,x
3
)=1− x
1
+
x
3
20
+ x
1
x
3
.
x
{pr}
1
=21,x
{pr}
3
=28,D
0
=2.5,r=2.
θ
θ = ρ arctan
D
4µ − D
2
D
2
− 2µ
sign(ρρ
pr
),
ρ
pr
f(x
1
,x
3
)=1+C
{x}
1
x
1
+ C
{y}
1
x
3
=1+0.4x
1
− x
3
.
V
MP
1
k
=1,V
MP
2
k
=1, 2
x
MP
1
1
(0) = 0,x
MP
1
3
(0) = 5,x
MP
1
2
(0) = 0, 5,x
MP
1
4
(0) = 0, 5,
x
MP
2
1
(0) = 60,x
MP
2
3
(0) = 20,x
MP
2
2
(0) = −0, 5,x
MP
2
4
(0) = −0, 5.

˙x
1
(t)=x
2
;
m
0
˙x
2
(t)=F
1
cos x
5
− F
2
sin x
5
+ ϑ
{1}
Σ
;
˙x
3
(t)=x
4
;
m
0
˙x
4
(t)=F
1
sin x
6
+ F
2
cos x
5
+ ϑ
{2}
Σ
;
˙x
5
(t)=x
6
;
J
0
˙x
6
(t)=M + ϑ
{3}
Σ
,
ϑ
{1}
Σ
,ϑ
{2}
Σ
,ϑ
{3}
Σ
F
1
=
m
4
j=1
f
j
pr
cos β
j
F
2
=
m
4
j=1
f
j
pr
sin β
j
M =
m
4
j=1
f
j
pr
(z
j
1
sin β
j
− z
j
2
cos β
j
)
ϑ
{1}
Σ
,ϑ
{2}
Σ
,ϑ
{3}
Σ
ϑ
{1}
Σ
= −
m
j=1
f
j
tr
sin β
j
− ∆m
ˆ
˙x
2
(t)+
m
j=1
f
j
prod
cos β
j
+ ϑ
{1}
;
ϑ
{2}
Σ
=
m
j=1
f
j
tr
cos β
j
− ∆m
ˆ
˙x
4
(t)+
m
j=1
f
j
prod
sin β
j
+ ϑ
{2}
;
ϑ
{3}
Σ
=
m
j=1
f
j
tr
(z
j
1
cos β
j
+ z
j
2
sin β
j
) − ∆J
ˆ
˙x
6
(t)+
+
m
j=1
f
j
prod
(z
j
1
sin β
j
− z
j
2
cos β
j
)+ϑ
{3}
,
f
j
tr
= −k
j
(−sin β
j
(x
2
cos x
5
+x
4
sin x
6
−z
j
2
x
5
)+cos β
j
(x
4
cos x
5
−x
2
sin x
5
+z
j
1
x
6
))
∆J ∆m
ϑ
{1}
ϑ
{2}
ϑ
{3}
ˆ
˙x
2
(t)
ˆ
˙x
4
(t)
ˆ
˙x
6
(t)
f
j
prod
= −µ
j
(cos β
j
(x
2
cos x
5
+ x
4
sin x
5
−z
j
2
x
6
)+sinβ
j
(x
4
cos x
6
−x
2
sin x
5
+ z
j
1
x
6
)
ν
j
k
j

ϑ
{1}
,ϑ
{2}
,ϑ
{3}
˙
ϑ
{1}
Σ
(t)=0;
˙
ϑ
{2}
Σ
(t)=0;
˙
ϑ
{3}
Σ
(t)=0.
ϑ
{1}
Σ
,ϑ
{2}
Σ
,ϑ
{3}
Σ
g(y, v, u)=g
0
(y, u)+G
1
(y)v.
y =
&
x
1
x
3
x
5
'
v =
&
ϑ
{1}
Σ
ϑ
{2}
Σ
ϑ
{3}
Σ
'
g
0
(y, u)=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
F
1
cos x
5
− F
2
sin x
5
m
0
F
1
sin x
5
+ F
2
cos x
5
m
0
M
J
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
, G
1
(y)=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
1
m
0
00
0
1
m
0
0
00
1
J
0
⎤
⎥
⎥
⎥
⎥
⎥
⎦
.
˙
z(t)=Lz − L
y
0
Γdy + Γg
0
(y, u);
ˆ
v =
y
0
Γdy − z,
Γ
Γ = −
(G
T
1
)
−1
L
T
T
,
L =
⎡
⎢
⎢
⎣
l
1
00
0 l
2
0
00l
3
⎤
⎥
⎥
⎦
