Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

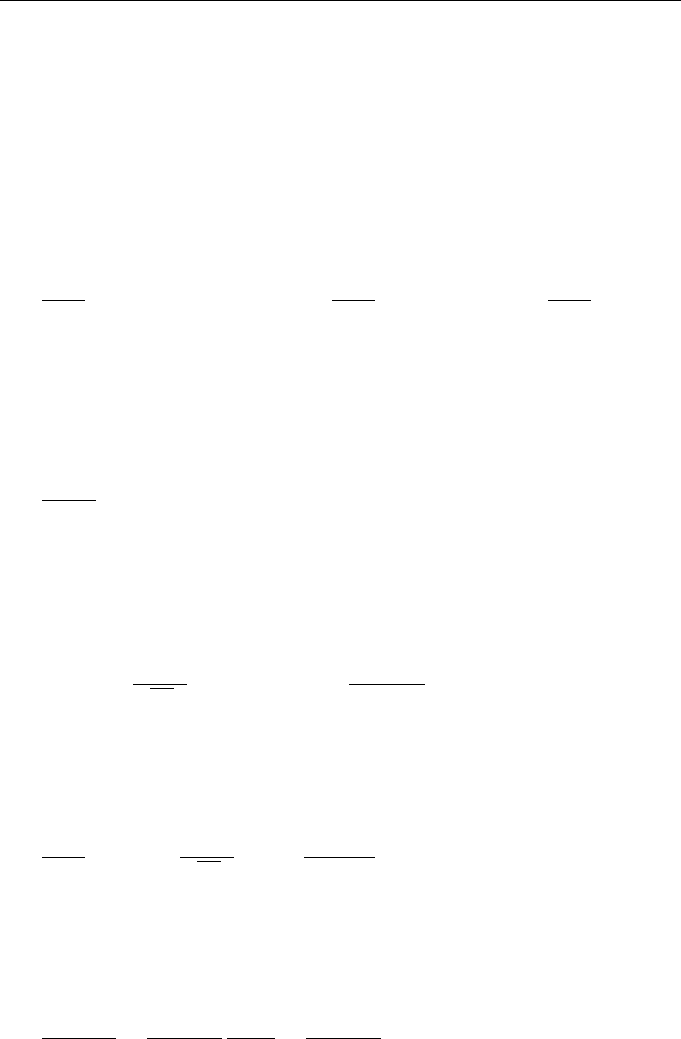
56 Lectures on Dynamics of Stochastic Systems

Consider now functional 8[ϕ(τ )] = F

[ϕ(τ )]F

[ϕ(τ )]. We have

δ8[ϕ(τ)] = F

[ϕ(τ ) + δϕ(τ )]F

[ϕ(τ ) + δϕ(τ )]−F

[ϕ(τ )]F

[ϕ(τ )]

= F

[ϕ(τ )]δF

[ϕ(τ )] +F

[ϕ(τ )]δF

[ϕ(τ )]

and, consequently,

δϕ(t)

[ϕ(τ )]F

[ϕ(τ )] = F

[ϕ(τ )]

δϕ(t)

[ϕ(τ )] +F

[ϕ(τ )]

δϕ(t)

[ϕ(τ )].

(2.5)

We can deﬁne the expression for the variational derivative of functional ϕ(τ

) with

respect to function ϕ(t) by the formal relationship

δϕ(τ

)

δϕ(t)

= δ(τ

− t). (2.6)

Formula (2.6) can be proved, for example, by considering the linear functional of the

form

F[ϕ(τ )] =

√

2πσ

∞

−∞

dτ ϕ(τ) exp



−

(τ − τ

)

2σ



. (2.7)

According to Eq. (2.3), the variational derivative of this functional has the form

δϕ(t)

F[ϕ(τ )] =

√

2πσ

exp

(

−

(

t − τ

)

2σ

)

. (2.8)

Performing now formal limit process σ → 0 in Eq. (2.7)) and (2.8), we obtain the

desired formula (2.6). Moreover,

δF[ϕ(τ)]

δϕ(t)

∂F[ϕ(τ)]

∂ϕ(τ )

δϕ(τ)

δϕ(t)

∂F[ϕ(τ)]

∂ϕ(τ )

δ(τ − t).

Solution Dependence on Problem Type, Medium Parameters, and Initial Data 57

Formula (2.6) is very convenient for functional differentiation of functionals

explicitly dependent on ϕ(τ ). Indeed, for the quadratic functional (b), we have

δϕ(t)

dτ

B(τ

, τ

)ϕ(τ

)

(2.5)

dτ

B(τ

, τ

)



δϕ(τ

)

δϕ(t)

ϕ(τ

) + ϕ(τ

)

δϕ(τ

)

δϕ(t)



(2.6)

dτ

[

B(t, τ )+B(τ, t)

]

ϕ(τ ) (t

< t < t

Consider the functional

F[ϕ(τ )] =

dτ L



τ, ϕ(τ ),

dϕ(τ )

dτ



as another example. In this case,

δϕ(t)

F[ϕ(τ )]

(2.4)

dτ







∂L



τ, ϕ(τ ),

dϕ(τ )

dτ



∂ϕ(τ )

∂L



τ, ϕ(τ ),

dϕ(τ )

dτ



∂ ˙ϕ(τ )

dτ







δϕ(τ)

δϕ(t)

(2.6)

dτ







∂L



τ, ϕ(τ ),

dϕ(τ )

dτ



∂ϕ(τ )

∂L



τ, ϕ(τ ),

dϕ(τ )

dτ



∂ ˙ϕ(τ )

dτ







δ(τ − t)



−

∂

∂ ˙ϕ(t)

∂

∂ϕ(t)





t, ϕ(t),

dϕ(t)



where ˙ϕ(t) =

ϕ(t) if point t belongs to interval (t

, t

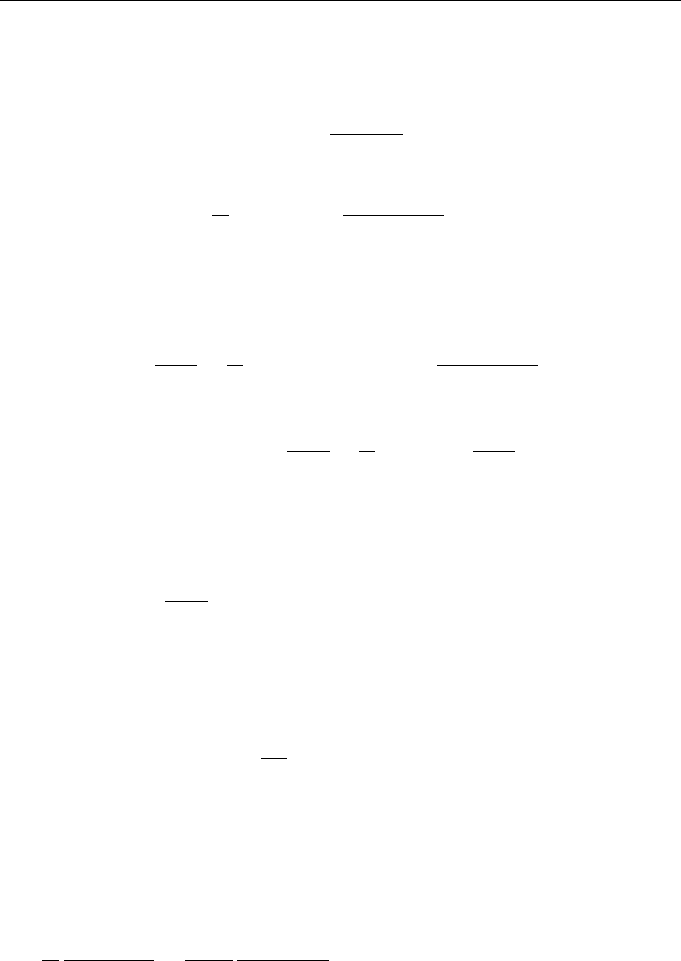
58 Lectures on Dynamics of Stochastic Systems

Just as a function can be expanded in the Taylor series, a functional F[ϕ(τ) +η(τ )]

can be expanded in the functional Taylor series in function η(τ ) for η(τ ) ∼ 0

F[ϕ(τ ) + η(τ )] = F[ϕ(τ)] +

∞

−∞

δF[ϕ(τ)]

δϕ(t)

η(t)

∞

−∞

∞

−∞

F[ϕ(τ )]

δϕ(t

)δϕ(t

)

η(t

)η(t

) + ··· . (2.9)

Note that the operator expression

1 +

∞

−∞

dtη(t)

δϕ(t)

∞

−∞

∞

−∞

η(t

)η(t

)

δϕ(t

)δϕ(t

)

+ ···

= 1 +

∞

−∞

dtη(t)

δϕ(t)





∞

−∞

dtη(t)

δϕ(t)





+ ··· (2.10)

can be written shortly as the operator

exp







∞

−∞

dtη(t)

δϕ(t)







, (2.11)

whose action should be treated precisely in the sense of expansion (2.10). Using this

operator, we can rewrite Eq. (2.9) in the form

F[ϕ(τ ) + η(τ )] = e

∞

−∞

dtη(t)

δϕ(t)

F[ϕ(τ )], (2.12)

which enables us to interpret operator (2.11) as the functional shift operator.

Consider now functional F[t;ϕ(τ )] dependent on parameter t. We can differentiate

this functional with respect to t and determine its variational derivative with respect to

ϕ(t

), as well. One can easily see that these operations commute, i.e., the equality

∂

∂t

δF[t;ϕ(τ )]

δϕ(t

)

δϕ(t

)

∂F[t ;ϕ(τ )]

∂t

(2.13)

holds. If the domain of τ is independent of t, the validity of Eq. (2.13) is obvious.

Otherwise, for example, for functionals F[t;ϕ(τ )] with 0 ≤ τ ≤ t, the validity of

Eq. (2.13) can be checked on by expanding functional F[t;ϕ(τ )] in the functional

Taylor series.

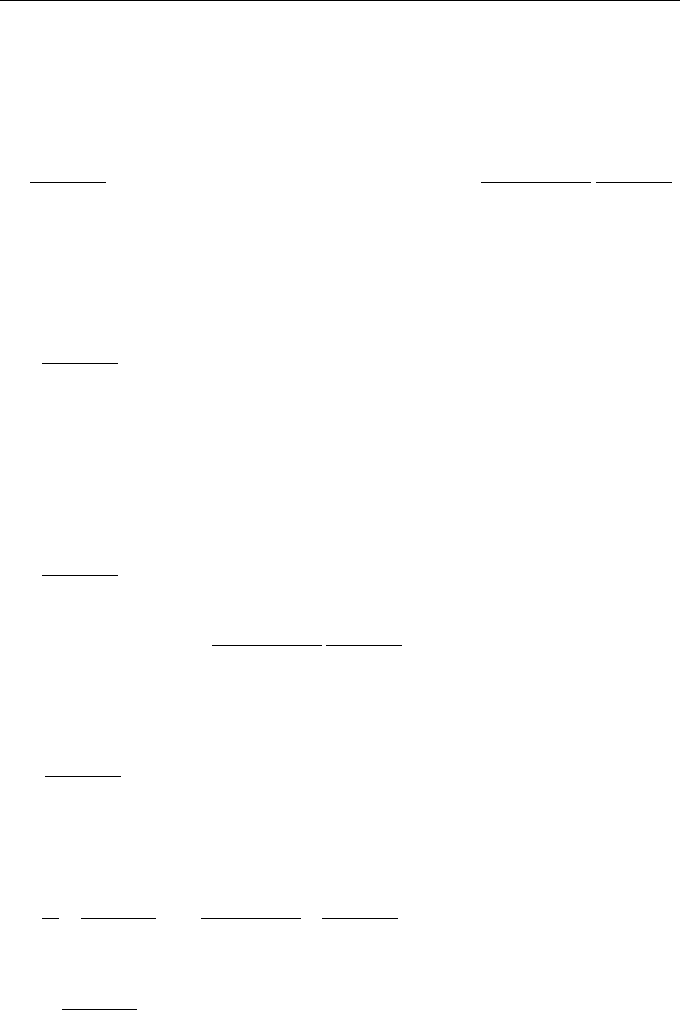
Solution Dependence on Problem Type, Medium Parameters, and Initial Data 59

2.1.2 Principle of Dynamic Causality

Vary Eq. (2.1) with respect to ﬁeld U

(

r, t

)

. Assuming that the initial position r

independent of ﬁeld U, we obtain the equation linear in variational derivative (the

linear variational differential equation)

δr

(

)

δU

(

r, t

)

= δ



r − r







− t





t − t



dτ

∂U

(

)

, τ

)

∂r

δr

(

)

δU

(

r, t

)

(2.14)

where δ



r − r



is the Dirac delta function, and θ

(

)

is the Heaviside step function.

From Eq. (2.14) follows that

δr

(

)

δU

(

r, t

)

= 0 for t

> t or t

< t

, (2.15)

which means that solution r(t) to the dynamic problem (2.1) as a functional of ﬁeld



r, t



depends on U



r, t



only for t

< t

< t. Consequently, function r(t) will

remain unchanged if ﬁeld U



r, t



varies outside the interval (t

, t), i.e., for t

< t

> t. We will call condition (2.15) the dynamic causality condition.

Taking this condition into account, we can rewrite Eq. (2.14) in the form

δr

(

)

δU

(

r, t

)

= δ



r − r







− t





t − t



dτ

∂U

(

)

, τ

)

∂r

δr

(

)

δU

(

r, t

)

. (2.16)

As a consequence, limit t → t

+ 0 yields the equality

δr

(

)

δU

(

r, t

)



t=t

= δ



r − r





. (2.17)

Integral equation (2.16) in variational derivative is obviously equivalent to the

linear differential equation with the initial value

∂

∂t



δr

(

)

δU

(

r, t

)



∂U

(

)

, t

)

∂r



δr

(

)

δU

(

r, t

)



δr

(

)

δU

(

r, t

)



t=t

= δ



r − r





(2.18)

The dynamic causality condition is the general property of problems described by

differential equations with initial values. The boundary-value problems possess no

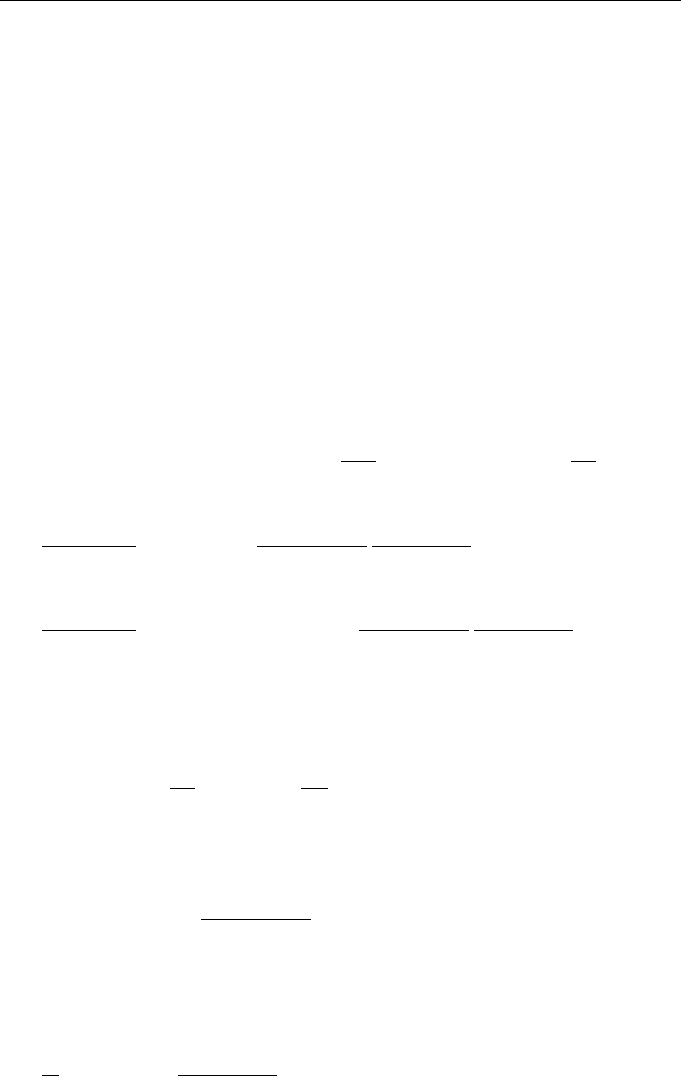
60 Lectures on Dynamics of Stochastic Systems

such property. Indeed, in the case of problem (1.31), (1.32), page 20–21 that describes

propagation of a plane wave in a layer of inhomogeneous medium, waveﬁeld u(x) at

point x and reﬂection and transmission coefﬁcients depend functionally on function

ε(x) for all x of layer (L

, L). However, using the imbedding method, we can convert

this problem into the initial-value problem with respect to an auxiliary parameter L and

make use the causality property in terms of the equations of the imbedding method.

2.2 Solution Dependence on Problem’s Parameters

2.2.1 Solution Dependence on Initial Data

Here, we will use the vertical bar symbol to isolate the dependence of solution r(t ) to

Eq. (2.1) on the initial parameters r

and t

(

)

= r

(

t|r

, t

)

, r

= r

(

, t

)

Let us differentiate Eq. (2.1) with respect to parameters r

and t

. As a result, we

obtain linear equations for Jacobi’s matrix

∂

∂r

(

t|r

, t

)

and quantity

∂

∂t

(

t|r

, t

)

∂r

(

t|r

, t

)

∂r

= δ

dτ

∂U

(

)

, τ

)

∂r

(

τ |r

, t

)

∂r

(

t|r

, t

)

∂t

= −U

(

), t

)

dτ

∂U

(

)

, τ

)

∂r

(

τ |r

, t

)

∂t

(2.19)

Multiplying now the ﬁrst of these equations by U

(

)

, t

)

, summing over index

k, adding the result to the second equation, and introducing the vector function

(

t|r

, t

)



∂

∂t

+ U

(

, t

)

∂

∂r



(

t|r

, t

)

we obtain that this function satisﬁes the linear homogeneous equation

(

t|r

, t

)

dτ

∂U

(

)

, τ

)

∂r

(

τ |r

, t

)

. (2.20)

Differentiating this equation with respect to time, we arrive at the ordinary differential

equation

∂

∂t

(

t|r

, t

)

∂U

(

)

, t

)

∂r

(

t|r

, t

)

Solution Dependence on Problem Type, Medium Parameters, and Initial Data 61

with the initial condition F

(

, t

)

= 0 at t = t

, which follows from Eq. (2.20); as

a consequence, we have F

(

t|r

, t

)

≡ 0. Therefore, we obtain the equality



∂

∂t

+ U

(

, t

)

∂

∂r



(

t|r

, t

)

= 0, (2.21)

which can be considered as the linear partial differential equation with the derivatives

with respect to variables r

, t

and the initial value at t

= t

(

t|r

, t

)

= r

. (2.22)

The variable t appears now in problem (2.21), (2.22) as a parameter.

Equation (2.21) is solved using the time direction inverse to that used in solving

problem (1.1), pages 50–51; for this reason, we will call it the backward equation.

Equation (2.21) with the initial condition (2.22) can be rewritten as the integral

equation

r(t|r

, t

) = r

dτ



(

, τ

)

∂

∂r



r(t|r

, τ ). (2.23)

Varying now Eq. (2.23) with respect to function U

, t

), we obtain the integral

equation

δr

(t|r

, t

)

δU

, t

)

= δ(r

− r

)θ(t

− t

)θ(t − t

)

∂r

(t|r

, t

)

∂r

dτ



(

, τ

)

∂

∂r



δr

(t|r

, τ )

δU

, t

)

, (2.24)

from which follows that

δr

(

t|r

, t

)

δU

(

, t

)

= 0, if t

> t or t

< t

which means that function r(t|r

, t

) also possesses the property of dynamic causality

with respect to parameter t

(2.15) – which is quite natural – and Eq. (2.24) can be

rewritten in the form (for t

< t

< t)

δr

(t|r

, t

)

δU

, t

)

= δ(r

− r

)

∂r

(t|r

, t

)

∂r

dτ



(

, τ

)

∂

∂r



δr

(t|r

, τ )

δU

, t

)

(2.25)

Setting now t

→ t

+ 0, we obtain the equality

δr

(

t|r

, t

)

δU

(

r, t

)



= δ

(

− r

)

∂r

(

t|r

, t

)

∂r

. (2.26)

62 Lectures on Dynamics of Stochastic Systems

2.2.2 Imbedding Method for Boundary-Value Problems

Consider ﬁrst boundary-value problems formulated in terms of ordinary differential

equations. The imbedding method (or invariant imbedding method, as it is usually

called in mathematical literature) offers a possibility of reducing boundary-value prob-

lems at hand to the evolution-type initial-value problems possessing the property of

dynamic causality with respect to an auxiliary parameter.

The idea of this method was ﬁrst suggested by V.A. Ambartsumyan (the so-called

Ambartsumyan invariance principle) [36–38] for solving the equations of linear theory

of radiative transfer. Further, mathematicians grasped this idea and used it to convert

boundary-value (nonlinear, in the general case) problems into evolution-type initial-

value problems that are more convenient for simulations. Several monographs (see,

e.g., [39–41]) deal with this method and consider both physical and computational

aspects.

Consider the dynamic system described in terms of the system of ordinary diffe-

rential equations

x(t) = F

(

t, x(t)

)

, (2.27)

deﬁned on segment t ∈ [0, T] with the boundary conditions

gx(0) + hx(T) = v, (2.28)

where g and h are the constant matrixes.

Dynamic problem (2.27), (2.28) possesses no dynamic causality property, which

means that the solution x(t) to this problem at instant t functionally depends on exter-

nal forces F

(

τ, x(τ)

)

for all 0 ≤ τ ≤ T. Moreover, even boundary values x(0) and

x(T) are functionals of ﬁeld F

(

τ, x(τ)

)

. The absence of dynamic causality in problem

(2.27), (2.28) prevents us from using the known statistical methods of analyzing sta-

tistical characteristics of the solution to Eq. (2.27) if external force functional F

(

t, x

)

is the random space- and time-domain ﬁeld. Introducing the one-time probability den-

sity P(t;x) of the solution to Eq. (2.27), we can easily see that condition (2.28) is

insufﬁcient for determining the value of this probability at any point. The boundary

condition imposes only certain functional restriction.

Note that the solution to problem (2.27), (2.28) parametrically depends on T and v,

i.e., x(t) = x(t;T, v). Abiding by paper [42], we introduce functions

R(T, v) = x(T;T, v), S(T, v) = x(0;T, v)

that describe the boundary values of the solution to Eq. (2.27).

Differentiate Eq. (2.27) with respect to T and v. We obtain two linear equations in

the corresponding derivatives

∂x

(t;T, v)

∂T

∂F

(t, x)

∂x

(t;T, v)

∂T

∂x

(t;T, v)

∂v

∂F

(t, x)

∂x

(t;T, v)

∂v

(2.29)

Solution Dependence on Problem Type, Medium Parameters, and Initial Data 63

These equations are identical in form; consequently, we can expect that their solutions

are related by the linear expression

∂x

(t;T, v)

∂T

= λ

(T, v)

∂x

(t;T, v)

∂v

, (2.30)

if vector quantity λ(T, v) is such that boundary conditions (2.28) are satisﬁed and the

solution is unique. To determine vector quantity λ(T, v), we ﬁrst set t = 0 in Eq. (2.30)

and multiply the result by matrix g; then, we set t = T and multiply the result by matrix

h; and, ﬁnally, we combine the obtained expressions. Taking into account Eq. (2.28),

we obtain

∂x(0;T, v)

∂T

+ h

∂x(t;T, v)

∂T



t=T

= λ(T, v).

In view of the fact that

∂x(t;T, v)

∂T



t=T

∂x(T;T, v)

∂T

−

∂x(t;T, v)

∂t



t=T

∂R(T, v)

∂T

− F

(

T, R(T, v)

)

(with allowance for Eq. (2.27)), we obtain the desired expression for quantity λ(T, v),

λ(T, v) = −hF

(

T, R(T, v)

)

. (2.31)

Expression (2.30) with parameter λ(T, v) deﬁned by Eq. (2.31), i.e., the expression

∂x

(t;T, v)

∂T

= −h

(

T, R(T, v)

)

∂x

(t;T, v)

∂v

, (2.32)

can be considered as the linear differential equation; one needs only to supplement it

with the corresponding initial condition

x(t;T, v)|

T=t

= R(t, v)

assuming that function R(T, v) is known.

The equation for this function can be obtained from the equality

∂R(T, v)

∂T

∂x(t;T, v)

∂t



t=T

∂x(t;T, v)

∂T



t=T

. (2.33)

The right-hand side of Eq. (2.33) is the sum of the right-hand sides of Eq. (2.27) and

(2.30) at t = T. As a result, we obtain the closed nonlinear (quasilinear) equation

∂R(T, v)

∂T

= −h

(

T, R(T, v)

)

∂R(T, v)

∂v

+ F

(

T, R(T, v)

)

. (2.34)

64 Lectures on Dynamics of Stochastic Systems

The initial condition for Eq. (2.34) follows from Eq. (2.28) for T → 0

R(T, v)|

T=0

= (g + h)

−1

v. (2.35)

Setting now t = 0 in Eq. (2.29), we obtain for the secondary boundary quantity

S(T, v) = x(0;T, v) the equation

∂S(T, v)

∂T

= −h

(

T, R(T, v)

)

∂S(T, v)

∂v

(2.36)

with the initial condition

S(T, v)|

T=0

= (g + h)

−1

following from Eq. (2.35).

Thus, the problem reduces to the closed quasilinear equation (2.34) with initial

value (2.35) and linear equation (2.30) whose coefﬁcients and initial value are deter-

mined by the solution of Eq. (2.34).

In the problem under consideration, input 0 and output T are symmetric. For this

reason, one can solve it not only from T to 0, but also from 0 to T. In the latter case,

functions R(T, v) and S(T, v) switch the places.

An important point consists in the fact that, despite the initial problem (2.27) is

nonlinear, Eq. (2.30) is the linear equation, because it is essentially the equation in

variations. It is Eq. (2.34) that is responsible for nonlinearity.

Note that the above technique of deriving imbedding equations for Eq. (2.27) can

be easily extended to the boundary condition of the form [42]

(

x(0)

)

+ h

(

x(T)

)

dτ K

(

τ, x(τ)

)

= v,

where g

(

)

, h

(

)

and K

(

T, x

)

are arbitrary given vector functions.

If function F

(

t, x

)

is linear in x, F

(

t, x

)

= A

(t)x

(t), then boundary-value prob-

lem (2.27), (2.28) assumes the simpler form

x(t) = A

(

)

x(t), gx(0) + hx(T) = v,

and the solution of Eq. (2.30), (2.34) and (2.36) will be the function linear in v

x(t;T, v) = X(t;T)v. (2.37)

As a result, we arrive at the closed matrix Riccati equation for matrix R(T) = X(T;T)

R(T) = A(T)R(T) − R(T)hA(T)R(T), R(0) = (g + h)

−1

. (2.38)

As regards matrix X(t, T), it satisﬁes the linear matrix equation with the initial

condition

∂

∂T

X(t;T) = −X(t;T)hA(T)R(T), X(t;T)

T=t

= R(t). (2.39)

Solution Dependence on Problem Type, Medium Parameters, and Initial Data 65

Problems

Problem 2.1

Helmholtz equation with unmatched boundary. Derive the imbedding equations

for the stationary wave boundary-value problem



+ k

(x)



u(x) = 0,



+ ik



u(x)



x=L

= 0,



− ik



u(x)



x=L

= −2ik

Instruction Reformulate this boundary-value problem as the initial-value in

terms of functions u(x) = u(x;L) and v(x;L) =

∂

∂x

u(x;L)

u(x;L) = v(x;L),

v(x;L) = −k

(x)u(x;L),

v(L

;L) + ik

u(L

;L) = 0, v(L;L) − ik

u(L;L) = −2ik

Solution

∂

∂L

u(x;L) =



(L) − k

u(L;L)



u(x;L),

u(x;L)|

L=x

= u(x;x),

u(L;L) = 2ik

[

u(L;L) − 1

]

(L) − k

u(L;L)

u(L

) =

+ k

Problem 2.2

Helmholtz equation with matched boundary. Derive the imbedding equations for

the stationary wave boundary-value problem



+ k

(x)



u(x;L) = 0,



+ ik



u(x;L)



x=L

= 0,



− ik(L)



u(x;L)



x=L

= −2ik(L).