Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.

This page intentionally left blank
Part II
Statistical Description of Stochastic
Systems
This page intentionally left blank

Lecture 4
Random Quantities, Processes, and
Fields
Prior to consider statistical descriptions of the problems mentioned in Lecture 1, we
discuss basic concepts of the theory of random quantities, processes, and fields.
4.1 Random Quantities and their Characteristics
The probability for a random quantity ξ to fall in interval −∞ < ξ < z is the mono-
tonic function
F(z) = P(−∞ < ξ < z) =
h
θ(z − ξ )
i
ξ
, F(∞) = 1, (4.1)
where
θ(z) =
1, if z > 0,
0, if z < 0,
is the Heaviside step function and
h
···
i
ξ
denotes averaging over an ensemble of real-
izations of random quantity ξ . This function is called the probability distribution
function or the integral distribution function. Definition (4.1) reflects the real-world
procedure of finding the probability according to the rule
P(−∞ < ξ < z) = lim
N→∞
n
N
,
where n is the integer equal to the number of realizations of event ξ < z in N indepen-
dent trials. Consequently, the probability for a random quantity ξ to fall into interval
z < ξ < z + dz, where dz is the infinitesimal increment, can be written in the form
P(z < ξ < z + dz) = P(z)dz,
where function P(z) called the probability density is represented by the formula
P(z) =
d
dz
P(−∞ < ξ < z) =
h
δ(z − ξ )
i
ξ
, (4.2)
Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00004-0
Copyright
c
2011 Elsevier Inc. All rights reserved.

90 Lectures on Dynamics of Stochastic Systems
where δ(z) is the Dirac delta function. In terms of probability density p(z), the integral
distribution function is expressed by the formula
F(z) = P(−∞ < ξ < z) =
z
Z
−∞
dξP(ξ ), (4.3)
so that
P(z) > 0,
∞
Z
−∞
dzP(z) = 1.
Multiplying Eq. (4.2) by arbitrary function f (z) and integrating over the whole
domain of variable z, we express the mean value of the arbitrary function of random
quantity in the following form
h
f (ξ )
i
ξ
=
∞
Z
−∞
dzP(z)f (z). (4.4)
The characteristic function defined by the equality
8(v) =
e
ivξ
ξ
=
∞
Z
−∞
dze
ivz
P(z)
is a very important quantity that exhaustively describes all characteristics of random
quantity ξ . The characteristic function being known, we can obtain the probability
density (via the Fourier transform)
P(x) =
1
2π
∞
Z
−∞
dv8(v)e
−ivx
,
moments
M
n
=
ξ
n
=
∞
Z
−∞
dzp(z)z
n
=
d
idv
n
8(v)
v=0
,
cumulants (or semi-invariants)
K
n
=
d
idv
n
2(v)
v=0
,

Random Quantities, Processes, and Fields 91
where 2(v) = ln 8(v), and other statistical characteristics. In terms of moments and
cumulants of random quantity ξ, functions 2(v) and 8(v) are the Taylor series
8(v) =
∞
X
n=0
i
n
n!
M
n
v
n
, 2(v) =
∞
X
n=1
i
n
n!
K
n
v
n
. (4.5)
In the case of multidimensional random quantity ξ = {z
1
, . . . , z
n
}, the exhaustive
statistical description assumes the multidimensional characteristic function
8(v) =
D
e
ivξ
E
ξ
, v = {v
1
, . . . , v
n
}. (4.6)
The corresponding joined probability density for quantities ξ
1
, . . . , ξ
n
is the Fourier
transform of characteristic function 8(v), i.e.,
P(x) =
1
(2π)
n
Z
dv8(v)e
−ivx
, x = {x
1
, . . . , x
n
}. (4.7)
Substituting function 8(v) defined by Eq. (4.6) in Eq. (4.7) and integrating the result
over v, we obtain the obvious equality
P(x) =
h
δ(ξ − x)
i
ξ
=
h
δ(ξ
1
− x
1
) . . . δ(ξ
n
− x
n
)
i
(4.8)
that can serve the definition of the probability density of random vector quantity ξ.
In this case, the moments and cumulants of random quantity ξ are defined by the
expressions
M
i
1
,...,i
n
=
∂
n
i
n
∂v
i
1
. . . ∂v
i
n
8(v)
v=0
, K
i
1
,...,i
n
=
∂
n
i
n
∂v
i
1
. . . ∂v
i
n
2(v)
v=0
,
where 2(v) = ln 8(v), and functions 2(v) and 8(v) are expressed in terms of
moments M
i
1
,...,i
n
and cumulants K
i
1
,...,i
n
via the Taylor series
8(v) =
∞
X
n=0
i
n
n!
M
i
1
,...,i
n
v
i
1
. . . v
i
n
, 2(v) =
∞
X
n=1
i
n
n!
K
i
1
,...,i
n
v
i
1
. . . v
i
n
. (4.9)
Note that, for quantities ξ assuming only discrete values ξ
i
(i = 1, 2, . . .) with
probabilities p
i
, formula (4.8) is replaced with its discrete analog
P
k
=
δ
z,ξ
k
,
where δ
i,k
is the Kronecker delta (δ
i,k
= 1 for i = k and 0 otherwise).
Consider now statistical average
h
ξf (ξ )
i
ξ
, where f (z) is arbitrary deterministic
function such that the above average exists. We calculate this average using the pro-
cedure that will be widely used in what follows. Instead of f (ξ ), we consider function

92 Lectures on Dynamics of Stochastic Systems
f (ξ + η), where η is arbitrary deterministic quantity. Expand function f (ξ + η) in the
Taylor series in powers of ξ , i.e., represent it in the form
f (ξ + η) =
∞
X
n=0
1
n!
f
(n)
(η)ξ
n
= exp
ξ
d
dη
f (η),
where we introduced the shift operator with respect to η. Then we can write the
equality
h
ξf (ξ + η)
i
ξ
=
ξ exp
ξ
d
dη
ξ
f (η)
=
ξ exp
ξ
d
dη
ξ
exp
ξ
d
dη
ξ
exp
ξ
d
dη
ξ
f (η) =
d
idη
h
f (ξ + η)
i
ξ
,
(4.10)
where function
(v) =
ξe
iξv
ξ
e
iξv
ξ
=
d
idv
ln 8(v) =
d
idv
2(v),
and 8(v) is the characteristic function of random quantity ξ . Using now the Taylor
series (4.5) for function 2(v), we obtain function (v) in the form of the series
(v) =
∞
X
n=0
i
n
n!
K
n+1
v
n
. (4.11)
Because variable η appears in the right-hand side of Eq. (4.10) only as the term of sum
ξ +η, we can replace differentiation with respect to η with differentiation with respect
to ξ (in so doing, operator (d/idξ ) should be introduced into averaging brackets)
and set η = 0. As a result, we obtain the equality
h
ξf (ξ )
i
ξ
=
d
idξ
f (ξ )
ξ
,
which can be rewritten, using expansion (4.11) for (v), as the series in cumulants K
n
h
ξf (ξ )
i
ξ
=
∞
X
n=0
1
n!
K
n+1
d
n
f (ξ )
dξ
n
ξ
. (4.12)
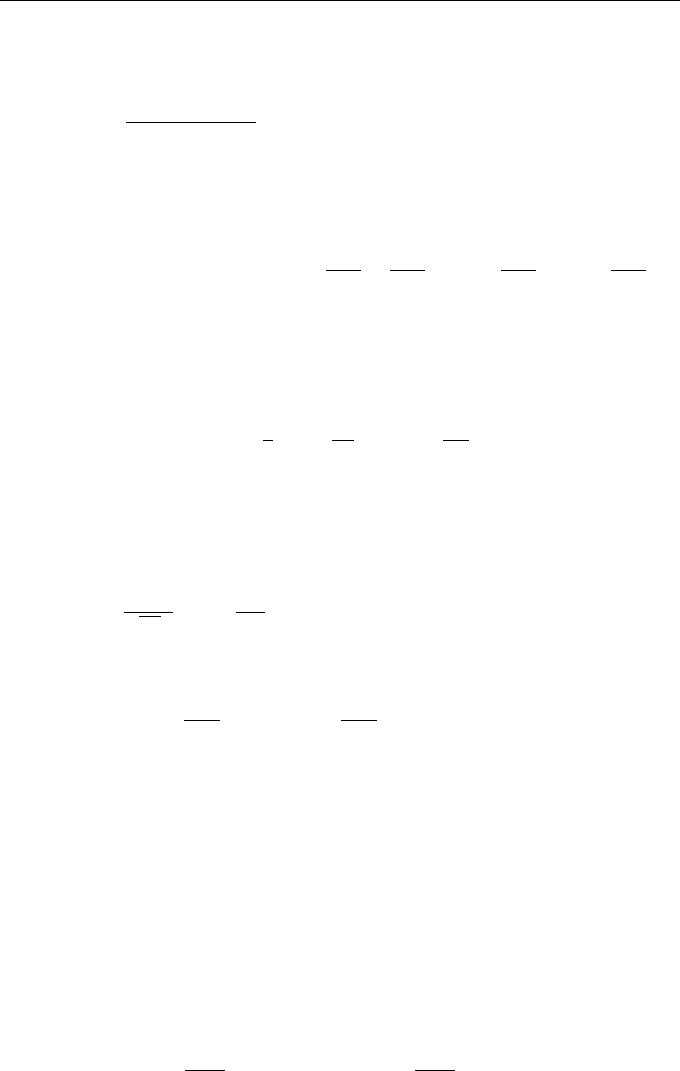
Random Quantities, Processes, and Fields 93
Note that, setting f (ξ) = ξ
n−1
in Eq. (4.12), we obtain the recurrence formula that
relates moments and cumulants of random quantity ξ in the form
M
n
=
n
X
k=1
(n − 1)!
(k − 1)!(n − k)!
K
k
M
n−k
(M
0
= 1, n = 1, 2, . . .). (4.13)
In a similar way, we can obtain the following operator expression for statistical
average
h
g(ξ)f (ξ )
i
ξ
h
g(ξ + η
1
)f (ξ + η
2
)
i
ξ
= exp
2
d
idη
1
+
d
idη
2
− 2
d
idη
1
− 2
d
idη
2
×
h
g(ξ + η
1
)
i
ξ
h
f (ξ + η
2
)
i
ξ
. (4.14)
In the particular case g(z) = e
ωz
, where parameter ω assumes complex values too, we
obtain the expression
e
ωξ
f (ξ + η)
ξ
= exp
2
1
i
ω +
d
dη
− 2
d
idη
h
f (ξ + η)
i
ξ
. (4.15)
To illustrate practicability of the above formulas, we consider two types of random
quantities ξ as examples.
1. Let ξ be the Gaussian random quantity with the probability density
P(z) =
1
√
2πσ
exp
(
−
z
2
2σ
2
)
.
Then, we have
8(v) = exp
(
−
v
2
σ
2
2
)
, 2(v) = −
v
2
σ
2
2
,
so that
M
1
= K
1
=
h
ξ
i
= 0, M
2
= K
2
= σ
2
=
D
ξ
2
E
, K
n>2
= 0.
In this case, the recurrence formula (4.13) assumes the form
M
n
= (n − 1)σ
2
M
n−2
, n = 2, . . . , (4.16)
from which follows that
M
2n+1
= 0, M
2n
= (2n − 1)!!σ
2n
.
For averages (4.12) and (4.15), we obtain the expressions
h
ξf (ξ )
i
ξ
= σ
2
df (ξ )
dξ
ξ
,
D
e
ωξ
f (ξ )
E
ξ
= exp
(
ω
2
σ
2
2
)
D
f (ξ + ωσ
2
)
E
ξ
. (4.17)

94 Lectures on Dynamics of Stochastic Systems
Additional useful formulas can be derived from Eqs. (4.17); for example,
D
e
ωξ
E
ξ
= exp
(
ω
2
σ
2
2
)
,
D
ξe
ωξ
E
ξ
= ωσ
2
exp
(
ω
2
σ
2
2
)
,
and so on.
If random quantity ξ has a nonzero mean value,
h
ξ
i
6= 0, the probability density is given
by the expression
P(z) =
1
√
2πσ
2
exp
(
−
(ξ −
h
ξ
i
)
2
2σ
2
)
. (4.18)
In this case, the characteristic function assumes the form
8(v) = exp
(
iv
h
ξ
i
−
v
2
σ
2
2
)
, 2(v) = iv
h
ξ
i
−
v
2
σ
2
2
,
and, consequently, moments and cumulants are given by the expressions
M
1
= K
1
=
h
ξ
i
, M
2
=
h
ξ
i
2
+ σ
2
, K
2
= σ
2
, K
n>2
= 0.
The corresponding integral distribution function (4.3) assumes the form
F(z) =
1
√
2πσ
2
z
Z
−∞
dξ exp
(
−
(ξ −
h
ξ
i
)
2
2σ
2
)
=
1
√
2π
z−
h
ξ
i
σ
Z
−∞
dy exp
(
−
y
2
2
)
= Pr
z −
h
ξ
i
σ
, (4.19)
where function
Pr
(
z
)
=
1
√
2π
z
Z
−∞
dx exp
(
−
x
2
2
)
(4.20)
is known as the probability integral. It is clear that
Pr(∞) = 1 and Pr(0) =
1
2
. (4.21)
For negative z (z < 0), this function satisfies the relationship
Pr
(
−|z|
)
=
1
√
2π
∞
Z
|z|
dx exp
(
−
x
2
2
)
= 1 − Pr
(
|z|
)
. (4.22)
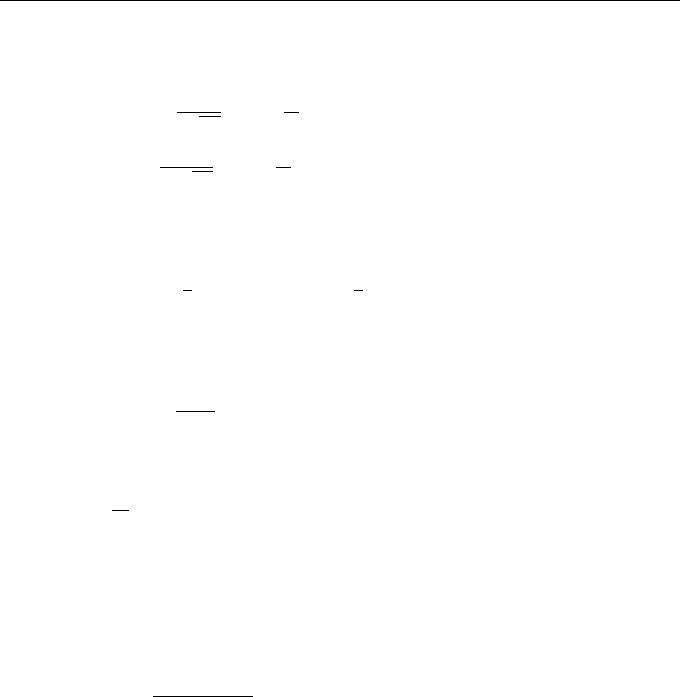
Random Quantities, Processes, and Fields 95
Asymptotic behavior of probability integral for z → ±∞ can be easily derived from
Eqs. (4.20) and (4.22); namely,
Pr
(
z
)
≈
1 −
1
z
√
2π
exp
(
−
z
2
2
)
, z → ∞,
1
|z|
√
2π
exp
(
−
z
2
2
)
z → −∞.
(4.23)
If we deal with the random Gaussian vector whose components are ξ
i
(
h
ξ
i
i
ξ
= 0, i =
1, . . . , n), then the characteristic function is given by the equality
8(v) = exp
−
1
2
B
ij
v
i
v
j
, 2(v) = −
1
2
B
ij
v
i
v
j
,
where matrix B
ij
=
ξ
i
ξ
j
and repeated indices assume summation. In this case, Eq. (4.17) is
replaced with the equality
h
ξf (ξ )
i
ξ
= B
df (ξ)
dξ
ξ
. (4.24)
2. Let ξ ≡ n be the integer random quantity governed by Poisson distribution
P
n
=
¯n
n
n!
e
−¯n
,
where ¯n is the average value of quantity n. In this case, we have
8(v) = exp
n
¯n
e
iv
− 1
o
, 2(v) = ¯n
e
iv
−1
.
The recurrence formula (4.13) and Eq. (4.12) assume for this random quantity the forms
M
l
= ¯n
l−1
X
k=0
(l −1)!
k!(l − 1 − k)!
M
k
≡ ¯n
D
(
n +1
)
l−1
E
,
h
nf (n)
i
= ¯n
h
f (n +1
i
. (4.25)
4.2 Random Processes, Fields, and their Characteristics
4.2.1 General Remarks
If we deal with random function (random process) z(t), then all statistical characteris-
tics of this function at any fixed instant t are exhaustively described in terms of the
one-time probability density
P(z, t) =
h
δ
(
z(t) − z
)
i
, (4.26)
dependent parametrically on time t by the following relationship
h
f (z(t))
i
=
∞
Z
−∞
dzf (z)P(z, t).
