Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

x Preface

considers asymptotic methods of dynamic system statistical analysis, such as the delta-

correlated random process (ﬁeld) approximation and diffusion approximation.

The third part deals with the analysis of speciﬁc physical problems associated with

coherent phenomena. These are clustering and diffusion of particles and passive tracer

(density and magnetic ﬁelds) in a random velocity ﬁeld, dynamic localization of plane

waves propagating in layered random media and caustic structure of waveﬁeld in ran-

dom multidimensional media. These phenomena are described by ordinary differential

equations and partial differential equations.

The material is supplemented with sections concerning dynamical and statistical

descriptions of simplest hydrodynamic-type systems, the relationship between con-

ventional methods (based on the Lyapunov stability analysis of stochastic dynamic

systems), methods of statistical topography and statistical description of magnetic ﬁeld

generation in the random velocity ﬁeld (stochastic [turbulent] dynamo).

Each lecture is appended with problems for the reader to solve on his or her own,

which will be a good training for independent investigations.

V. I. Klyatskin

Moscow, Russia

Introduction

Different areas of physics pose statistical problems in ever greater numbers. Apart

from issues traditionally obtained in statistical physics, many applications call for

including ﬂuctuation effects. While ﬂuctuations may stem from different sources (such

as thermal noise, instability, and turbulence), methods used to treat them are very sim-

ilar. In many cases, the statistical nature of ﬂuctuations may be deemed known (either

from physical considerations or from problem formulation) and the physical processes

may be modeled by differential, integro-differential or integral equations.

We will consider a statistical theory of dynamic and wave systems with ﬂuctuating

parameters. These systems can be described by ordinary differential equations, partial

differential equations, integro-differential equations and integral equations. A popular

way to solve such systems is by obtaining a closed system of equations for statistical

characteristics, to study their solutions as comprehensively as possible.

We note that wave problems are often boundary-value problems. When this is the

case, one may resort to the imbedding method to reformulate the equations at hand to

initial-value problems, thus considerably simplifying the statistical analysis.

The purpose of this book is to demonstrate how different physical problems descri-

bed by stochastic equations can be solved on the basis of a general approach.

In stochastic problems with ﬂuctuating parameters, the variables are functions. It

would be natural therefore to resort to functional methods for their analysis. We will

use a functional method devised by Novikov [1] for Gaussian ﬂuctuations of parame-

ters in a turbulence theory and developed by the author of this book [2] for the general

case of dynamic systems and ﬂuctuating parameters of an arbitrary nature.

However, only a few dynamic systems lend themselves to analysis yielding solu-

tions in a general form. It proved to be more efﬁcient to use an asymptotic method

where the statistical characteristics of dynamic problem solutions are expanded in

powers of a small parameter. This is essentially a ratio of the random impact’s cor-

relation time to the time of observation or to another characteristic time scale of the

problem (in some cases, these may be spatial rather than temporal scales). This method

is essentially a generalization of the theory of Brownian motion. It is termed the delta-

correlated random process (ﬁeld) approximation.

For dynamic systems described by ordinary differential stochastic equations with

Gaussian ﬂuctuations of parameters, this method leads to a Markovian problem solv-

ing model, and the respective equation for transition probability density has the form

of the Fokker–Planck equation. In this book, we will consider in depth the methods

of analysis available for this equation and its boundary conditions. We will analyze

solutions and validity conditions by way of integral transformations. In more com-

plicated problems described by partial differential equations, this method leads to a

xii Introduction

generalized equation of the Fokker–Planck type in which variables are the derivatives

of the solution’s characteristic functional. For dynamic problems with non-Gaussian

ﬂuctuations of parameters, this method also yields Markovian type solutions. Under

the circumstances, the probability density of respective dynamic stochastic equations

satisﬁes a closed operator equation.

In physical investigations, Fokker–Planck and similar equations are usually set up

from rule-of-thumb considerations, and dynamic equations are invoked only to cal-

culate the coefﬁcients of these equations. This approach is inconsistent, generally

speaking. Indeed, the statistical problem is completely deﬁned by dynamic equations

and assumptions on the statistics of random impacts. For example, the Fokker–Planck

equation must be a logical sequence of the dynamic equations and some assumptions

on the character of random impacts. It is clear that not all problems lend themselves

for reduction to a Fokker–Planck equation. The functional approach allows one to

derive a Fokker–Planck equation from the problem’s dynamic equation along with its

applicability conditions. In terms of formal mathematics, our approach corresponds to

that of R.L. Stratonovich (see, e.g., [3]).

For a certain class of Markovian random process (telegrapher’s processes, Gaussian

process and the like), the developed functional approach also yields closed equations

for the solution probability density with allowance for a ﬁnite correlation time of ran-

dom interactions.

For processes with Gaussian ﬂuctuations of parameters, one may construct a

better physical approximation than the delta-correlated random process (ﬁeld)

approximation – the diffusion approximation that allows for ﬁniteness of correlation

time radius. In this approximation, the solution is Markovian and its applicability con-

dition has transparent physical meaning, namely, the statistical effects should be small

within the correlation time of ﬂuctuating parameters. This book treats these issues in

depth from a general standpoint and for some speciﬁc physical applications.

Recently, the interest of both theoreticians and experimenters has been attracted to

the relation of the behavior of average statistical characteristics of a problem solution

with the behavior of the solution in certain happenings (realizations). This is espe-

cially important for geophysical problems related to the atmosphere and ocean where,

generally speaking, a respective averaging ensemble is absent and experimenters, as a

rule, deal with individual observations.

Seeking solutions to dynamic problems for these speciﬁc realizations of medium

parameters is almost hopeless due to the extreme mathematical complexity of these

problems. At the same time, researchers are interested in the main characteristics of

these phenomena without much need to know speciﬁc details. Therefore, the idea of

using a well-developed approach to random processes and ﬁelds based on ensem-

ble averages rather than separate observations proved to be very fruitful. By way of

example, almost all physical problems of the atmosphere and ocean to some extent are

treated by statistical analysis.

Randomness in medium parameters gives rise to a stochastic behavior of physical

ﬁelds. Individual samples of scalar two-dimensional ﬁelds ρ(R, t), R = (x, y), say,

recall a rough mountainous terrain with randomly scattered peaks, troughs, ridges and

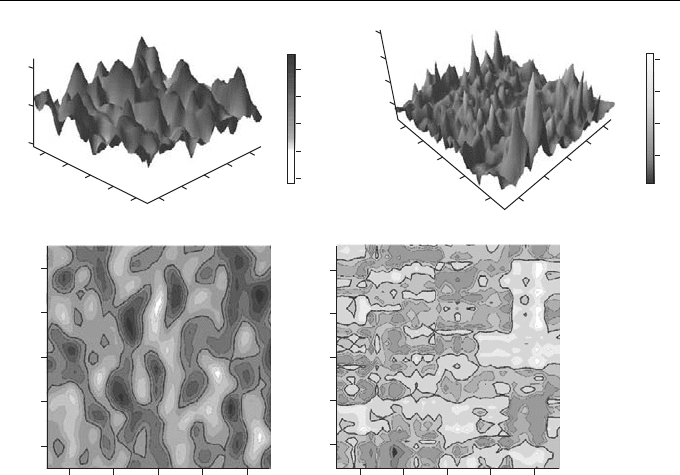
Introduction xiii

Figure 0.1 Realizations of the ﬁelds governed by (a) Gaussian and (b) lognormal distribution

and the corresponding topographic level lines. The bold curves in the bottom patterns show

level lines corresponding to levels 0 (a) and 1 (b).

saddles. Figure 0.1 shows examples of realizations of two random ﬁelds characterized

by different statistical structures.

Common methods of statistical averaging (computing mean-type averages –

(

R, t

)

, space-time correlation function –



(

R, t

)



, t



etc., where

· · ·

implies averaging over an ensemble of random parameter samples) smooth the quali-

tative features of speciﬁc samples. Frequently, these statistical characteristics have

nothing in common with the behavior of speciﬁc samples, and at ﬁrst glance may

even seem to be at variance with them. For example, the statistical averaging over

all observations makes the ﬁeld of average concentration of a passive tracer in a

random velocity ﬁeld ever more smooth, whereas each realization sample tends to

be more irregular in space due to the mixture of areas with substantially different

concentrations.

Thus, these types of statistical average usually characterize ‘global’ space–time

dimensions of the area with stochastic processes, but give no details about the process

behavior inside the area. For this case, details heavily depend on the velocity ﬁeld

pattern, speciﬁcally, on whether it is divergent or solenoidal. Thus, the ﬁrst case will

show with total probability that clusters will be formed, i.e. compact areas of enhanced

concentration of tracer surrounded by vast areas of low-concentration tracer. In the

−

140

120

100

80 80100 100120 120140 14060 60

100

140

(a) (b)

−1

−2

140

100

140

xiv Introduction

circumstances, all statistical moments of the distance between the particles will grow

with time exponentially; that is, on average, a statistical recession of particles will take

place [4].

In a similar way, in the case of waves propagating in random media, an exponential

spread of the rays will take place on average; but simultaneously, with total probability,

caustics will form at ﬁnite distances. One more example to illustrate this point is the

dynamic localization of plane waves in layered randomly inhomogeneous media. In

this phenomenon, the wave ﬁeld intensity exponentially decays inward to the medium

with the probability equal to unity when the wave is incident on the half-space of such

a medium, while all statistical moments increase exponentially with distance from the

boundary of the medium [5].

These physical processes and phenomena occurring with the probability equal to

unity will be referred to as coherent processes and phenomena [6]. This type of sta-

tistical coherence may be viewed as some organization of the complex dynamic sys-

tem, and retrieval of its statistically stable characteristics is similar to the concept of

coherence as self-organization of multicomponent systems that evolve from the ran-

dom interactions of their elements [7]. In the general case, it is rather difﬁcult to say

whether or not the phenomenon occurs with the probability equal to unity. However,

for a number of applications amenable to treatment with the simple models of ﬂuctu-

ating parameters, this may be handled by analytical means. In other cases, one may

verify this by performing numerical modeling experiments or analyzing experimental

ﬁndings.

The complete statistic (say, the whole body of all n-point space-time moment func-

tions), would undoubtedly contain all the information about the investigated dynamic

system. In practice, however, one may succeed only in studying the simplest statistical

characteristics associated mainly with simultaneous and one-point probability distri-

butions. It would be reasonable to ask how with these statistics on hand one would

look into the quantitative and qualitative behavior of some system happenings?

This question is answered by methods of statistical topography [8]. These meth-

ods were highlighted by Ziman [9], who seems to have coined this term. Statistical

topography yields a different philosophy of statistical analysis of dynamic stochastic

systems, which may prove useful for experimenters planning a statistical processing

of experimental data. These issues are treated in depth in this book.

More details about the material of this book and more exhaustive references can be

found in the textbook quoted in reference [2] and recent reviews [6, 10–16].

Part I

Dynamical Description of Stochastic

Systems

This page intentionally left blank

Lecture 1

Examples, Basic Problems, Peculiar

Features of Solutions

In this chapter, we consider several dynamic systems described by differential equa-

tions of different types and discuss the features in the behaviors of solutions to these

equations under random disturbances of parameters. Here, we content ourselves with

the problems in the simplest formulation. More complete formulations will be dis-

cussed below, in the sections dealing with statistical analysis of the corresponding

systems.

1.1 Ordinary Differential Equations: Initial-Value Problems

1.1.1 Particles Under the Random Velocity Field

In the simplest case, a particle under random velocity ﬁeld is described by the system

of ordinary differential equations of the ﬁrst order

r(t) = U(r, t), r(t

) = r

, (1.1)

where U(r, t) = u

(r, t) + u(r, t), u

(r, t) is the deterministic component of the

velocity ﬁeld (mean ﬂow), and u(r, t) is the random component. In the general case,

ﬁeld u(r, t) can have both nondivergent (solenoidal, for which div u(r, t) = 0) and

divergent (for which div u(r, t) 6= 0) components.

We dwell on stochastic features of the solution to problem (1.1) for a system of par-

ticles in the absence of mean ﬂow (u

(r, t) = 0). From Eq. (1.1) formally follows that

every particle moves independently of other particles. However, if random ﬁeld u(r, t)

has a ﬁnite spatial correlation radius l

cor

, particles spaced by a distance shorter than

cor

appear in the common zone of infection of random ﬁeld u(r, t) and the behavior

of such a system can show new collective features.

For steady velocity ﬁeld u(r, t) ≡ u(r), Eq. (1.1) reduces to

r(t) = u(r), r(0) = r

. (1.2)

Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00001-5

4 Lectures on Dynamics of Stochastic Systems

This equation clearly shows that steady points er (at which u(er ) = 0) remain the ﬁxed

points. Depending on whether these points are stable or unstable, they will attract or

repel nearby particles. In view of randomness of function u(r), points er are random

too.

It is expected that the similar behavior will be also characteristic of the general case

of space-time random velocity ﬁeld u(r,t).

If some points er remain stable during sufﬁciently long time, then clusters of partic-

les (i.e., compact regions with elevated particle concentration, which occur merely in

rareﬁed zones) must arise around these points in separate realizations of random ﬁeld

u(r, t). On the contrary, if the stability of these points alternates with instability sufﬁ-

ciently rapidly and particles have no time for signiﬁcant rearrangement, no clusters of

particles will occur.

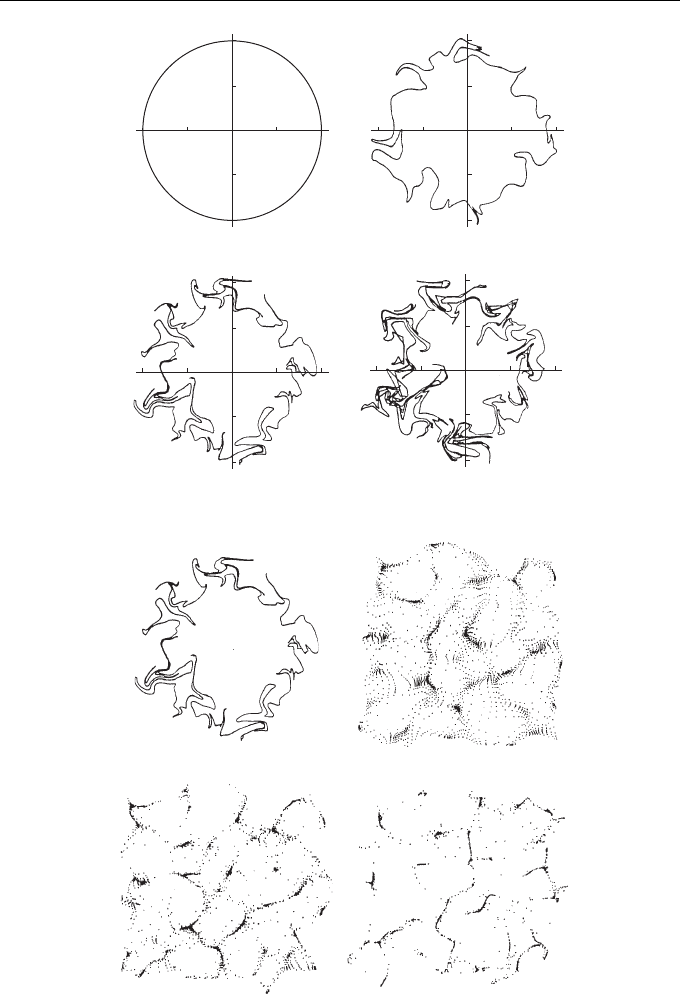
Simulations [17, 18] show that the behavior of a system of particles essentially

depends on whether the random ﬁeld of velocities is nondivergent or divergent. By

way of example, Fig. 1.1a shows a schematic of the evolution of the two-dimensional

system of particles uniformly distributed within the circle for a particular realization

of the nondivergent steady ﬁeld u(r).

Here, we use the dimensionless time related to statistical parameters of ﬁeld u(r).

In this case, the area of surface patch within the contour remains intact and partic-

les relatively uniformly ﬁll the region within the deformed contour. The only feature

consists in the fractal-type irregularity of the deformed contour. This phenomenon –

called chaotic advection – is under active study now (see, e.g., [19]).

On the contrary, in the case of the divergent velocity ﬁeld u(r), particles uniformly

distributed in the square at the initial instant will form clusters during the temporal

evolution. Results simulated for this case are shown in Fig. 1.1b. We emphasize that

the formation of clusters is purely a kinematic effect. This feature of particle dynamics

disappears on averaging, over an ensemble of realizations of random velocity ﬁeld.

To demonstrate the process of particle clustering, we consider the simplest prob-

lem [11], in which random velocity ﬁeld u(r, t) has the form

u(r, t) = v(t)f (kr), (1.3)

where v(t) is the random vector process and

f (kr) = sin 2(kr) (1.4)

is the deterministic function of one variable. This form of function f (kr) corresponds

to the ﬁrst term of the expansion in harmonic components and is commonly used in

numerical simulations [17, 18].

In this case, Eq. (1.1) can be written in the form

r(t) = v(t) sin 2(kr), r(0) = r

In the context of this model, motions of a particle along vector k and in the plane

perpendicular to vector k are independent and can be separated. If we direct the x-axis

Examples, Basic Problems, Peculiar Features of Solutions 5

510

−5−10

−10

510

−5−10

−10

510

−5−10

−10

−5

510

−5

−10

−5

t = 0

t = 4t = 3

t = 0

t = 2

(a)

(b)

t = 0.5

t = 1 t = 2.0

Figure 1.1 Diffusion of a system of particles described by Eqs. (1.2) numerically simulated

for (a) solenoidal and (b) nondivergent random steady velocity ﬁeld u(r).