Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

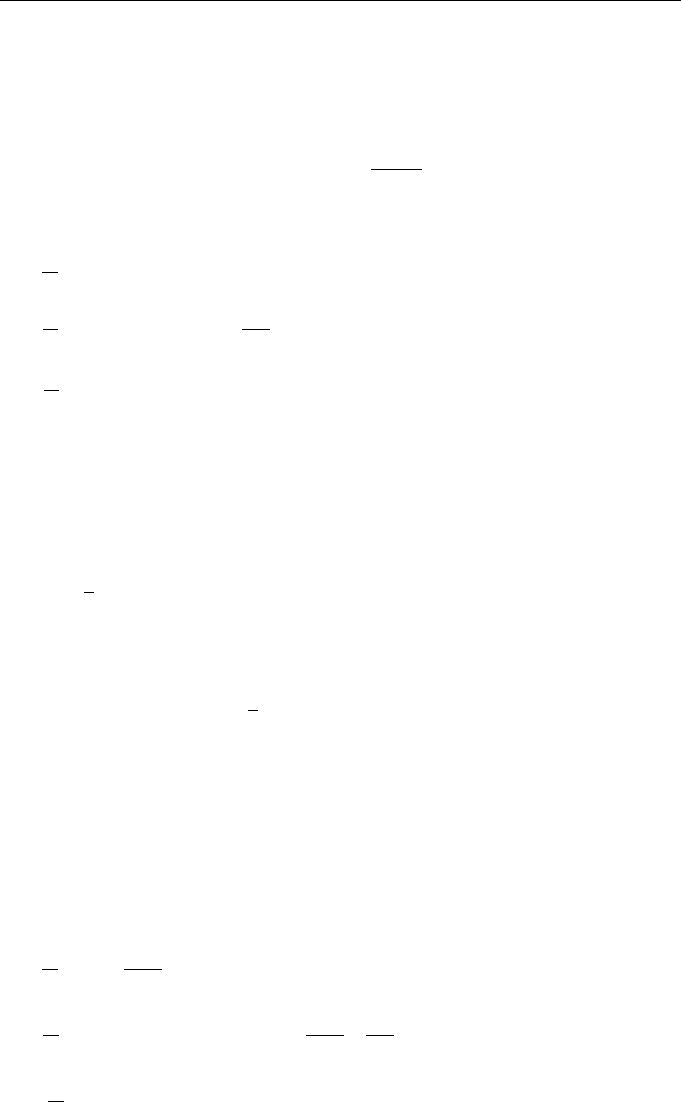
16 Lectures on Dynamics of Stochastic Systems

that have the integral of motion

2,3

(t)v

2,4

(t) = I = const.

Introducing notation

x(t) = v

1,0

(t), y(t) = v

1,2

(t), z(t) =

2,4

(t)

2,3

(t)

we arrive at the system of three equations

x(t) = −y

(t) + 1,

y(t) = x(t)y(t) + QI



z(t)

− z(t)



z(t) = y(t)z(t),

(1.25)

that describes the behavior of the seven-mode model (1.24).

Inclusion of the second stage signiﬁcantly changes the dynamics of the ﬁrst stage.

Indeed, the initial-values of components v

2,3

and v

2,4

being arbitrarily small, they

nevertheless determine certain value of the integral of motion I, and, by virtue of

Eqs. (1.25), variable y will repeatedly change the sign.

Consider the case of small values of constant I in more detail. Figure 1.7 shows the

numerical solution of Eqs. (1.25) with the initial conditions x = 0.05, y = 1, and z = 1

at Q =

√

8 and I = 10

−20

. As may be seen, two types of motion are characteristic

of system (1.25) for small values of constant I; namely, ‘fast’ motions occur in a

small vicinity of either closed trajectory of the Hamiltonian system (1.19) near the

plane z = 1, and relatively rare hopping events occur due to the changes of sign

of variable y at z ∼ I or z ∼ −

. Every such hopping event signiﬁcantly changes the

parameters of fast motion trajectories of system (1.25), so that the motion of the system

acquires the features characteristic of the dynamic systems with strange attractors (see,

e.g., [26]).

To describe ‘slow’ motions, we introduce variables X and Y by the formulas

x(t) = X(t)x

(t), y(t) = Y(t)y

(t),

where

(

(t), y

(t)

)

is a solution to Eqs. (1.19). According to Eqs. (1.25), X(t), Y(t),

and z(t) satisfy the equations

X(t) =

(t)

h

(t) − Y

(t)



(t) + 1 − X(t)

Y(t) =

(

X(t) − 1

)

Y(t)x

(t) +

(t)



z(t)

− z(t)



z(t) = 2QY(t)y

(t)z(t).

Examples, Basic Problems, Peculiar Features of Solutions 17

−10

−20

−1

−2

log zy

100

(a) (b)

0.5

−0.5

0.5

−0.5

−1

Figure 1.7 (a) Time-dependent behavior of components of system (1.25) (curve 1 for y and

curve 2 for log z) and (b) projection of the phase trajectory of system (1.25) on plane (x, y).

Averaging these equations in slow varying quantities over the period

√

2π,

we obtain

X(t) = 0,

Y(t) = QI



Z(t)

− Z(t)



Z(t) = 2QY(t)Z(t), (1.26)

where Z =ez(t). The system (1.26) has the integral of motion

= Y

(t) + I



Z(t)

+ Z(t)



, (1.27)

so that we can use the corresponding variables to rewrite it in the Hamiltonian form, as

it was done for the system (1.19). The motion of system (1.26) along closed trajectories

around steady point (0, 1) is characterized by the half-period T

(the time between

hopping events) given by the formula

− I



+ Z





r +

√

− 1







√

− 1

r +

√

− 1





This expression for T

appears to be quite adequate for the solution shown in Fig. 1.7. On closed trajecto-

ries of system (1.19) near which this solution passes, the values of Hamiltonian do not exceed 2. Because

these trajectories are located in small vicinities of critical points (0, 1) and (0, −1) of this system, we

performed averaging assuming thatey

(t) = 1 and

1/y

(t) = 1.

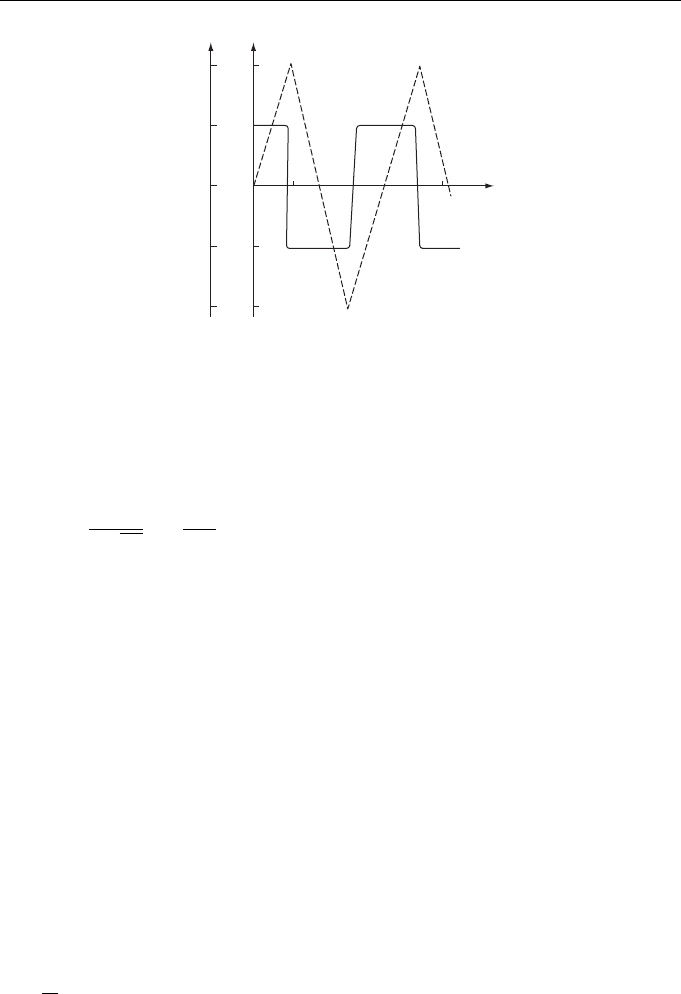
18 Lectures on Dynamics of Stochastic Systems

−10

−20

−1

−2

log Z Y

Figure 1.8 Time-dependent behavior of components of system (1.26) (curve 1 for Y and curve

2 for log Z ).

where Z

and Z

are the roots of Eq. (1.27) at Y = 0, r = 2H

/I, and K(z) is the

complete elliptic integral of the ﬁrst kind. For small I, we have

≈

√





. (1.28)

Figure 1.8 shows the numerical solution of Eqs. (1.26) with the initial condi-

tions Y = 1, Z = 1 (they correspond to the initial conditions used earlier for

solving Eqs. (1.25)), constants Q and I also being coincident with those used for

solving Eqs. (1.25). The comparison of curves in Figs. 1.7 and 1.8 shows that system

(1.26) satisfactorily describes hopping events in system (1.25). The values of half-

period T

determined by Eq. (1.28) and obtained from the numerical integration of

Eqs. (1.25) are 33.54 and 33.51, respectively. We note that system (1.25) has an addi-

tional characteristic time T

∼ 1/Q, whose meaning is the duration of the hopping

event.

1.1.4 Systems with Blow-Up Singularities

The simplest stochastic system showing singular behavior in time is described by the

equation commonly used in the statistical theory of waves,

x(t) = −λx

(t) + f (t), x(0) = x

, λ > 0, (1.29)

where f (t) is the random function of time.

Examples, Basic Problems, Peculiar Features of Solutions 19

x(t)

Figure 1.9 Typical realization of the solution to Eq. (1.29).

In the absence of randomness ( f (t) = 0), the solution to Eq. (1.29) has the form

x(t) =

(

t − t

)

, t

= −

λx

For x

> 0, we have t

< 0, and solution x(t) monotonically tends to zero with

increasing time. On the contrary, for x

< 0, solution x(t) reaches −∞ within a ﬁnite

time t

= −1/λx

, which means that the solution becomes singular and shows the

blow-up behavior. In this case, random force f (t) has insigniﬁcant effect on the beha-

vior of the system. The effect becomes signiﬁcant only for positive parameter x

Here, the solution, slightly ﬂuctuating, decreases with time as long as it remains

positive. On reaching sufﬁciently small value x(t), the impact of force f (t) can cause

the solution to hop into the region of negative values of x, where it reaches the value

of −∞ within a certain ﬁnite time.

Thus, in the stochastic case, the solution to problem (1.29) shows the blow-up

behavior for arbitrary values of parameter x

and always reaches −∞ within a ﬁnite

time t

. Figure 1.9 schematically shows the temporal realization of the solution x(t) to

problem (1.29) for t > t

; its behavior resembles a quasi-periodic structure.

1.1.5 Oscillator with Randomly Varying Frequency (Stochastic

Parametric Resonance)

In the above stochastic examples, we considered the effect of additive random impacts

(forces) on the behavior of systems. The simplest nontrivial system with multiplica-

tive (parametric) impact can be illustrated by the example of stochastic parametric

resonance. Such a system is described by the second-order equation

x(t) + ω

[1 + z(t)]x(t) = 0,

x(0) = x

x(0) = v

(1.30)

20 Lectures on Dynamics of Stochastic Systems

ε (x)

(a) (b)

LLL

ik(L

−x)

ik(L

−x)

− ik(L−x)

ik(L−x)

ε (x)

Figure 1.10 (a) Plane wave incident on the medium layer and (b) source inside the medium

layer.

where z(t) is the random function of time. This equation is characteristic of almost

all ﬁelds of physics. It is physically obvious that dynamic system (1.30) is capable of

parametric excitation, because random process z(t) has harmonic components of all

frequencies, including frequencies 2ω

/n (n = 1, 2, . . .) that exactly correspond to

the frequencies of parametric resonance in the system with periodic function z(t), as,

for example, in the case of the Mathieu equation.

1.2 Boundary-Value Problems for Linear Ordinary

Differential Equations (Plane Waves in Layered Media)

In the previous section, we considered several dynamic systems described by a sys-

tem of ordinary differential equations with given initial-values. Now, we consider the

simplest linear boundary-value problem, namely, the steady one-dimensional wave

problem.

Assume the layer of inhomogeneous medium occupies part of space L

< x < L,

and let the unit-amplitude plane wave u

(

)

= e

−ik

(

x−L

)

is incident on this layer from

the region x > L (Fig. 1.10a).

The waveﬁeld satisﬁes the Helmholtz equation,

u(x) + k

(x)u(x) = 0, (1.31)

where

(x) = k

[1 + ε(x)],

and function ε(x) describes medium inhomogeneities. We assume that ε(x) = 0, i.e.,

k(x) = k outside the layer; inside the layer, we set ε(x) = ε

(x) + iγ , where the real

part ε

(x) is responsible for wave scattering in the medium and the imaginary part

γ  1 describes absorption of the wave in the medium.

In region x > L, the waveﬁeld has the structure

u(x) = e

−ik(x−L)

+ R

ik(x−L)

Examples, Basic Problems, Peculiar Features of Solutions 21

where R

is the complex reﬂection coefﬁcient. In region x < L

, the structure of the

waveﬁeld is

u(x) = T

ik(L

−x)

where T

is the complex transmission coefﬁcient. Boundary conditions for Eq. (1.31)

are the continuity conditions for the ﬁeld and the ﬁeld derivative at layer boundaries;

they can be written as follows

u(L) +

du(x)



x=L

= 2, u(L

) −

du(x)



x=L

= 0. (1.32)

Thus, the waveﬁeld in the layer of an inhomogeneous medium is described by the

boundary-value problems (1.31), (1.32). Dynamic equation (1.31) coincides in form

with Eq. (1.30). Note that the problem under consideration assumes that function ε(x)

is discontinuous at layer boundaries. We will call the boundary-value problem (1.31),

(1.32) the unmatched boundary-value problem. In such problems, wave scattering is

caused not only by medium inhomogeneities, but also by discontinuities of function

ε(x) at layer boundaries.

If medium parameters (function ε

(x)) are speciﬁed in the statistical form, then

solving the stochastic problem (1.31), (1.32) consists in obtaining statistical characte-

ristics of the reﬂection and transmission coefﬁcients, which are related to the waveﬁeld

values at layer boundaries by the relationships

= u(L) − 1, T

= u(L

and the waveﬁeld intensity

I(x) = |u(x)|

inside the inhomogeneous medium. Determination of these characteristics constitutes

the subject of the statistical theory of radiative transfer.

Note that, for x < L, from (1.31) follows the equality

kγ I(x) =

S(x),

where energy-ﬂux density S(x) is determined by the relationship

S(x) =



u(x)

∗

(x) − u

∗

(x)

u(x)



By virtue of boundary conditions, we have S(L) = 1 −|R

and S(L

) = |T

For non-absorptive media (γ = 0), conservation of energy-ﬂux density is expressed

by the equality

+ |T

= 1. (1.33)

22 Lectures on Dynamics of Stochastic Systems

2.5 5

Figure 1.11 Dynamic localization phenomenon simulated for two realizations of medium

inhomogeneities.

Consider some features characteristic of solutions to the stochastic boundary-value

problem (1.31), (1.32). On the assumption that medium inhomogeneities are absent

(ε

(x) = 0) and absorption γ is sufﬁciently small, the intensity of the waveﬁeld in the

medium slowly decays with distance according to the exponential law

I(x) = |u(x)|

= e

−kγ (L−x)

. (1.34)

Figure 1.11 shows two realizations of the intensity of a wave in a sufﬁciently thick

layer of medium. These realizations were simulated for two realizations of medium

inhomogeneities. The difference between them consists in the fact that the correspon-

ding functions ε

(x) have different signs in the middle of the layer at a distance of the

wavelength. This offers a possibility of estimating the effect of a small medium mis-

match on the solution of the boundary problem. Omitting the detailed description of

problem parameters, we mention only that this ﬁgure clearly shows the prominent ten-

dency of a sharp exponential decay (accompanied by signiﬁcant spikes toward both

higher and nearly zero-valued intensity values), which is caused by multiple reﬂec-

tions of the wave in the chaotically inhomogeneous random medium (the phenomenon

of dynamic localization). Recall that absorption is small (γ  1), so that it cannot sig-

niﬁcantly affect the dynamic localization.

The imbedding method offers a possibility of reformulating boundary-value prob-

lem (1.31), (1.32) to the dynamic initial-value problem with respect to parameter L

(this parameter is the geometrical position of the layer right-hand boundary) by consid-

ering the solution to the boundary-value problem as a function of parameter L (see the

next lecture). On such reformulation, the reﬂection coefﬁcient R

satisﬁes the Riccati

equation

= 2ikR

ε(L)

(

1 + R

)

, R

= 0, (1.35)

Examples, Basic Problems, Peculiar Features of Solutions 23

and the waveﬁeld in the medium layer u(x) ≡ u(x;L) satisﬁes the linear equation

∂

∂L

u(x;L) = iku(x;L) +

ε(L)

(

1 + R

)

u(x;L),

u(x;x) = 1 + R

(1.36)

The equation for the reﬂection coefﬁcient squared modulus W

= |R

for absent

attenuation (i.e., at γ = 0) follows from Eq. (1.35)

= −

(L)



− R

∗



(

1 − W

)

, W

= 0. (1.37)

Note that condition W

= 1 will be the initial condition to Eq. (1.37) in the case

of totally reﬂecting boundary at L

. In this case, the wave incident on the layer of a

non-absorptive medium (γ = 0) is totally reﬂected from the layer, i.e., W

= 1.

In the general case of arbitrarily reﬂecting boundary L

, the steady-state (indepen-

dent of L) solution W

= 1 corresponding to the total reﬂection of incident wave for-

mally exists for a half-space (L

→ −∞) ﬁlled with non-absorptive random medium,

too. This solution, as it will be shown later, is actually realized in the statistical prob-

lem with a probability equal to unity.

If, in contrast to the above problem, we assume that function k(x) is continuous at

boundary x = L, i.e., if we assume that the wave number in the free half-space x > L

is equal to k(L), then boundary conditions (1.32) of problem (1.31) will be replaced

with the conditions

u(L) +

k(L)

du(x)



x=L

= 2, u(L

) −

k(L

)

du(x)



x=L

= 0. (1.38)

We will call the boundary-value problem (1.31), (1.38) the matched boundary-value

problem.

The ﬁeld of a point source located in the layer of random medium is descri-

bed by the similar boundary-value problem for Green’s function of the Helmholtz

equation:

G(x;x

) + k

[1 + ε(x)]G(x;x

) = 2ikδ(x − x

G(L;x

) +

dG(x;x

)



x=L

= 0, G(L

) −

dG(x;x

)



x=L

= 0.

Outside the layer, the solution has the form of outgoing waves (Fig. 1.10b)

G(x;x

) = T

(

x−L

)

(x ≥ L), G(x;x

) = T

−ik

(

x−L

)

(x ≤ L

Note that, for the source located at the layer boundary x

= L, this problem coin-

cides with the boundary-value problem (1.31), (1.32) on the wave incident on the

layer, which yields

G(x;L) = u(x;L).

24 Lectures on Dynamics of Stochastic Systems

1.3 Partial Differential Equations

Consider now several dynamic systems (dynamic ﬁelds) described by partial differen-

tial equations.

1.3.1 Linear First-Order Partial Differential Equations

Diffusion of Density Field Under Random Velocity Field

In the context of linear ﬁrst-order partial differential equations, the simplest problems

concern the equation of continuity for the concentration of a conservative tracer and

the equation of transfer of a nonconservative passive tracer by random velocity ﬁeld

U(r, t):



∂

∂t

∂

∂r

U(r, t)



ρ(r, t) = 0, ρ(r, 0) = ρ

(r), (1.39)



∂

∂t

+ U(r, t)

∂

∂r



q(r, t) = 0, q(r, 0) = q

(r). (1.40)

The conservative tracer is a tracer whose total mass remains intact

drρ(r, t) =

drρ

(r) (1.41)

We can use the method of characteristics to solve the linear ﬁrst-order partial diffe-

rential equations (1.39), (1.40). Introducing characteristic curves (particles)

r(t) = U(r, t), r(0) = r

, (1.42)

we can write these equations in the form

ρ(t) = −

∂U (r, t)

∂r

ρ(t), ρ(0) = ρ

q(t) = 0, q(0) = q

(1.43)

This formulation of the problem corresponds to the Lagrangian description, while the

initial dynamic equations (1.39), (1.40) correspond to the Eulerian description.

Here, we introduced the characteristic vector parameter r

in the system of equa-

tions (1.42), (1.43). With this parameter, Eq. (1.42) coincides with Eq. (1.1) that des-

cribes particle dynamics under random velocity ﬁeld.

The solution of system of equations (1.42), (1.43) depends on initial-value r

r(t) = r(t|r

), ρ(t) = ρ(t|r

), (1.44)

which we will isolate in the argument list by the vertical bar.

Examples, Basic Problems, Peculiar Features of Solutions 25

The ﬁrst equality in Eq. (1.44) can be considered as the algebraic equation in cha-

racteristic parameter; the solution of this equation

= r

(r, t)

exists because divergence j(t|r

) = det

∂r

(t|r

)/∂r

is different from zero. Conse-

quently, we can write the solution of the initial equation (1.39) in the form

ρ(r, t) = ρ(t|r

(r, t)) =

ρ(t|r

)j(t|r

)δ

(

r(t|r

) − r

)

Integrating this expression over r, we obtain, in view of Eq. (1.41), the relationship

between functions ρ(t|r

) and j(t|r

)

ρ(t|r

) =

)

j(t|r

)

, (1.45)

and, consequently, the density ﬁeld can be rewritten in the form of equality

ρ(r, t) =

ρ(t|r

)j(t|r

)δ

(

r(t|r

) − r

)

)δ

(

r(t|r

) − r

)

(1.46)

that ascertains the relationship between the Lagrangian and Eulerian characteristics.

For the position of the Lagrangian particle, the delta-function appeared in the right-

hand side of this equality is the indicator function (see Lecture 3).

For a nondivergent velocity ﬁeld (div U(r, t) = 0), both particle divergence and

particle density are conserved, i.e.,

j(t|r

) = 1, ρ(t|r

) = ρ

), q(t|r

) = q

Consider now the stochastic features of solutions to problem (1.39). A convenient

way of analyzing dynamics of a random ﬁeld consists in using topographic concepts.

Indeed, in the case of the nondivergent velocity ﬁeld, temporal evolution of the con-

tour of constant concentration ρ = const coincides with the dynamics of particles

under this velocity ﬁeld and, consequently, coincides with the dynamics shown in

Fig. 1.1a. In this case, the area within the contour remains constant and, as it is seen

from Fig. 1.1a, the pattern becomes highly indented, which is manifested in gradient

sharpening and the appearance of contour dynamics for progressively shorter scales.

In the other limiting case of a divergent velocity ﬁeld, the area within the contour tends

to zero, and the concentration ﬁeld condenses in clusters. One can ﬁnd examples simu-

lated for this case in papers [17, 18]. These features of particle dynamics disappear on

averaging over an ensemble of realizations.

Cluster formation in the Eulerian description can be traced using the random velo-

city ﬁeld of form (1.3), (1.4), page 4. If v

(t) 6= 0, then concentration ﬁeld in