Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

6 Lectures on Dynamics of Stochastic Systems

along vector k, then the equations assume the form

x(t) = v

(t) sin(2kx), x(0) = x

R(t) = v

(t) sin(2kx), R(0) = R

(1.5)

The solution of the ﬁrst equation in system (1.5) is

x(t) =

arctan

T(t)

tan(kx

)

, (1.6)

where

T(t) = 2k

dτ v

(τ ). (1.7)

Taking into account the equalities following from Eq. (1.6)

sin(2kx) =

sin(2kx

)

−T(t)

cos

(kx

) + e

T(t)

sin

(kx

)

cos(2kx) =

1 − e

2T(t)

tan

(kx

)

1 + e

2T(t)

tan

(kx

)

(1.8)

we can rewrite the second equation in Eqs. (1.5) in the form

R(t|r

) =

sin(2kx

(t)

−T(t)

cos

(kx

) + e

T(t)

sin

(kx

)

As a result, we have

R(t|r

) = R

dτ

sin(2kx

(τ )

−T(τ)

cos

(kx

) + e

T(τ)

sin

(kx

)

. (1.9)

Consequently, if the initial particle position x

is such that

= n

, (1.10)

where n = 0, ±1, . . . , then the particle will be the ﬁxed particle and r(t) ≡ r

Equalities (1.10) deﬁne planes in the general case and points in the one-dimensional

case. They correspond to zeros of the ﬁeld of velocities. Stability of these points

depends on the sign of function v(t), and this sign changes during the evolution pro-

cess. It can be expected that particles will gather around these points if v

(t) 6= 0,

which just corresponds to clustering of particles.

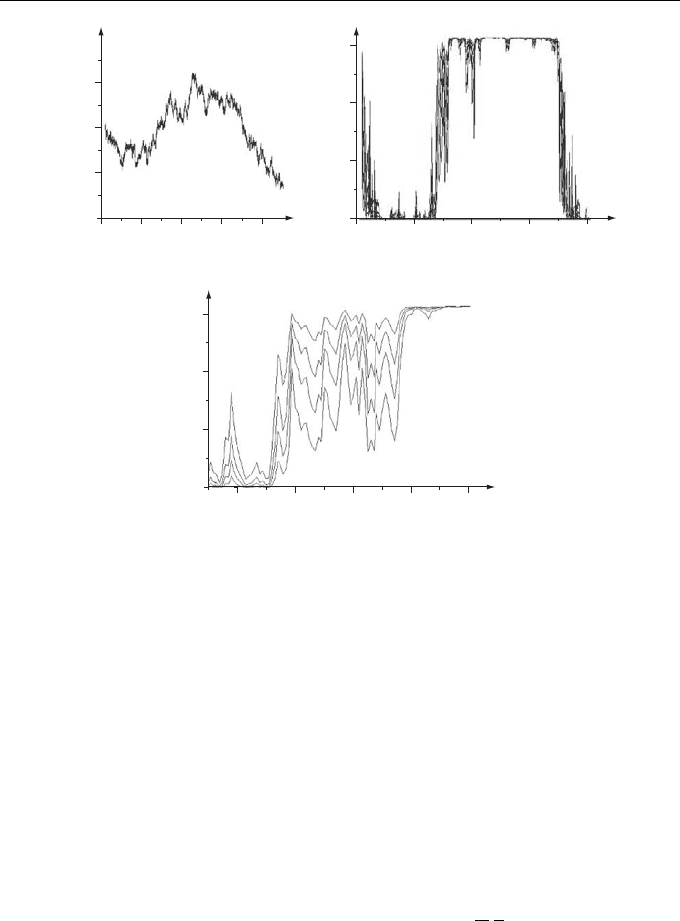
Examples, Basic Problems, Peculiar Features of Solutions 7

13 14 15 16 17

0.5

1.0

1.5

010203040

0.5

1.0

1.5

010203040

−

(a) (b)

(c)

T (t )

Figure 1.2 (a) Segment of a realization of random process T(t) obtained by numerically integ-

rating Eq. (1.7) for a realization of random process v

(t); (b), (c) x-coordinates simulated with

this segment for four particles versus time.

In the case of a nondivergent velocity ﬁeld, v

(t) = 0 and, consequently, T(t) ≡ 0;

as a result, we have

x(t|x

) ≡ x

, R(t|r

) = R

+ sin 2(kx

)

dτ v

(τ ),

which means that no clustering occurs.

Figure 1.2a shows a fragment of the realization of random process T(t) obtained by

numerical integration of Eq. (1.7) for a realization of random process v

(t); we used

this fragment for simulating the temporal evolution of coordinates of four particles

x(t), x ∈ (0, π/2) initially located at coordinates x

(i) =

(i = 1, 2, 3, 4) (see

Fig. 1.2b). Figure 1.2b shows that particles form a cluster in the vicinity of point x = 0

at the dimensionless time t ≈ 4. Further, at time t ≈ 16 the initial cluster disappears

and new one appears in the vicinity of point x = π/2. At moment t ≈ 40, the cluster

appears again in the vicinity of point x = 0, and so on. In this process, particles

in clusters remember their past history and signiﬁcantly diverge during intermediate

temporal segments (see Fig. 1.2c).

Thus, we see in this example that the cluster does not move from one region

to another; instead, it ﬁrst collapses and then a new cluster appears. Moreover, the

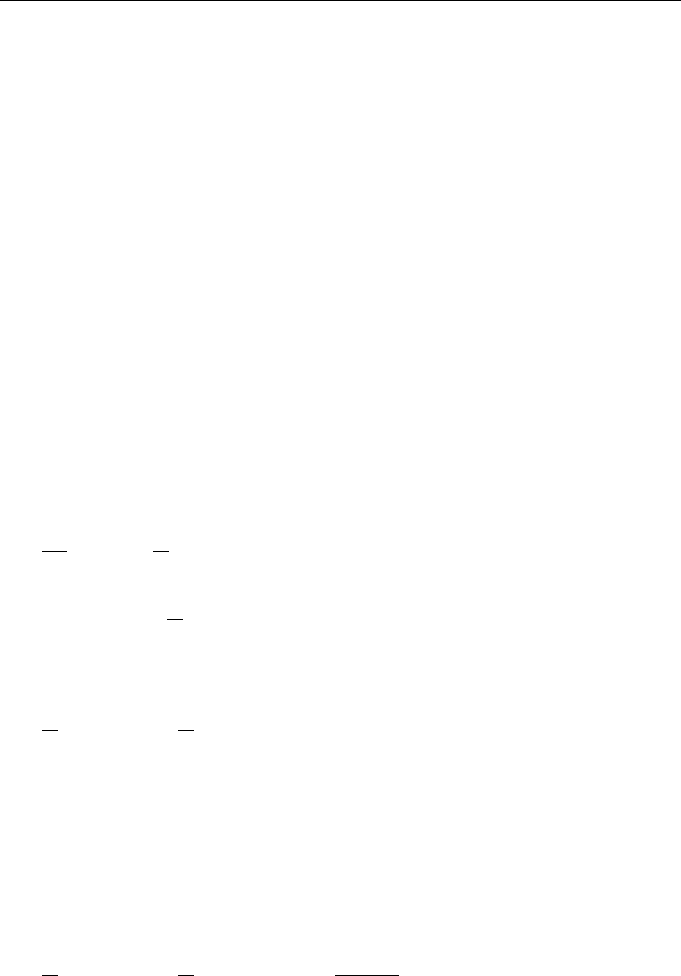
8 Lectures on Dynamics of Stochastic Systems

lifetime of clusters signiﬁcantly exceeds the duration of intermediate segments. It

seems that this feature is characteristic of the speciﬁc model of velocity ﬁeld and

follows from steadiness of points (1.10).

As regards the particle diffusion along the y-direction, no cluster occurs there.

Note that such clustering in a system of particles was found, to all appearance for

the ﬁrst time, in papers [20, 21] as a result of simulating the so-called Eole experiment

with the use of the simplest equations of atmospheric dynamics.

In this global experiment, 500 constant-density balloons were launched in

Argentina in 1970–1971; these balloons traveled at a height of about 12 km and spread

along the whole of the southern hemisphere.

Figure 1.3 shows the balloon distribution over the southern hemisphere for day 105

from the beginning of this process simulation [20]; this distribution clearly shows that

balloons are concentrated in groups, which just corresponds to clustering.

1.1.2 Particles Under Random Forces

The system of equations (1.1) describes also the behavior of a particle under the ﬁeld

of random external forces f(r, t). In the simplest case, the behavior of a particle in the

presence of linear friction is described by the differential equation of the second order

(Newton equation)

r(t) = −λ

r(t) + f (r, t),

r(0) = r

r(0) = v

(1.11)

or the systems of differential equation of the ﬁrst order

r(t) = v(t),

v(t) = −λv(t) + f (r, t),

r(0) = r

, v(0) = v

(1.12)

Results of numerical simulations of stochastic system (1.12) can be found in Refs

[22, 23]. Stability of the system was studied in these papers by analyzing Lyapunov’s

characteristic parameters.

The behavior of a particle under the deterministic potential ﬁeld in the presence of

linear friction and random forces is described by the system of equations

r(t) = v(t),

v(t) = −λv(t) −

∂U(r, t)

∂r

+ f (r, t),

r(0) = r

, v(0) = v

(1.13)

which is the simplest example of Hamiltonian systems with linear friction. If friction

and external forces are absent and function U is independent of time, U(r, t) = U(r),

Examples, Basic Problems, Peculiar Features of Solutions 9

Figure 1.3 Balloon distribution in the atmosphere for day 105 from the beginning of process

simulation.

the system has an integral of motion

E(t) = const, E(t) =

+ U(r)

expressing energy conservation.

In statistical problems, equations of type (1.12), (1.13) are widely used to describe

the Brownian motion of particles.

In the general case, Hamiltonian systems are described by the system of equations

r(t) =

∂H(r, v, t)

∂v

v(t) = −

∂H(r, v, t)

∂r

r(0) = r

, v(0) = v

(1.14)

where H(r, v, t) = H(r(t), v(t), t) is the Hamiltonian function. In the case of conser-

vative Hamiltonian systems, function H(r, v, t) has no explicit dependence on time,

H(r, v, t) = H(r, v), and the system has the integral of motion

H(r, v) = const.

10 Lectures on Dynamics of Stochastic Systems

1.1.3 The Hopping Phenomenon

Now, we dwell on another stochastic aspect related to dynamic equations of type (1.1);

namely, we consider the hopping phenomenon caused by random ﬂuctuations.

Consider the one-dimensional nonlinear equation

x(t) = x



1 − x



+ f (t), x(0) = x

, (1.15)

where f (t) is the random function of time. In the absence of randomness ( f (t) ≡ 0),

the solution of Eq. (1.15) has two stable steady states x = ±1 and one instable state

x = 0. Depending on the initial-value, solution of Eq. (1.15) arrives at one of the stable

states. However, in the presence of small random disturbances f (t), dynamic system

(1.15) will ﬁrst approach the vicinity of one of the stable states and then, after the lapse

of certain time, it will be transferred into the vicinity of another stable state.

Note that Eq. (1.15) corresponds to limit process λ → ∞ in the equation

x(t) + λ

x(t) − λ



dU(x)

+ f (t)



= 0,

that is known as the Dufﬁng equation and is the special case of the one-dimensional

Hamiltonian system (1.13)

x(t) = v(t),

v(t) = −λ



v(t) −

dU(x)

− f (t)



(1.16)

with the potential function

U(x) =

−

In other words, Eq. (1.15) corresponds to great friction coefﬁcients λ.

Statistical description of this problem will be considered in Sect. 8.4.1, page 211.

Additionally, we note that, in the context of statistical description, reduction of the

Hamiltonian system (1.16) to the ‘short-cut equation’ is called the Kramers problem.

It is clear that the similar behavior can occur in more complicated situations.

Hydrodynamic-Type Nonlinear Systems

An important problem of studying large-scale processes in the atmosphere considered

as a single physical system consists in revealing the mechanism of energy exchange

between different ‘degrees of freedom’. The analysis of such nonlinear processes on

the base of simple models described by a small number of parameters (degrees of

freedom) is recently of great attention. In this connection, A.M. Obukhov (see, for

example [24]) introduced the concept of hydrodynamic-type systems (HTS). These

systems have a ﬁnite number of parameters v

. . . , v

, but the general features of the

dynamic equations governing system motions coincide with those characteristic of the

Examples, Basic Problems, Peculiar Features of Solutions 11

hydrodynamic equations of perfect incompressible liquid, including quadratic nonlin-

earity, energy conservation, and regularity (phase volume invariance during system

motions). The general description of HTS is given in Sect. 8.3.3, page 200. Here, we

dwell only on the dynamic description of simplest systems.

The simplest system of this type (S

) is equivalent to the Euler equations in the

dynamics of solids; it describes the known problem on liquid motions in an ellipsoidal

cavity [24]. Any ﬁnite-dimensional approximation of hydrodynamic equations also

belongs to the class of HTS if it possesses the above features.

To model the cascade mechanism of energy transformation in a turbulent ﬂow,

Obukhov [25] suggested a multistage HTS. Each stage of this system consists of

identical-scale triplets; at every next stage, the number of triplets is doubled and the

scale is decreased in geometrical progression with ratio Q & 1. As a result, this model

describes interactions between the motions of different scales.

The ﬁrst stage consists of a singe triplet whose unstable mode v

is excited by an

external force f

(t) applied to the system (Fig. 1.4a). The stable modes of this triplet

1,1

and v

1,2

are the unstable modes of two triplets of the second stage; their stable

modes v

2,1

, v

2,2

, v

2,3

, and v

2,4

are, in turn, the unstable modes of four triplets of the

third stage; and so on (Fig. 1.4b).

It should be noted however that physical processes described in terms of macro-

scopic equations occur in actuality against the background of processes charac-

terized by shorter scales (noises). Among these processes are, for example, the

molecular noises (in the context of macroscopic hydrodynamics), microturbulence

(against the large-scale motions), and the effect of truncated (small-scale) terms in

the ﬁnite-dimensional approximation of hydrodynamic equations. The effect of these

small-scale noises should be analyzed in statistical terms. Such a consideration can be

performed in terms of macroscopic variables. With this goal, one must include exter-

nal random forces with certain statistical characteristics in the corresponding macro-

scopic equations. The models considered here require additionally the inclusion of

dissipative terms in the equations of motion to ensure energy outﬂow to smaller-scale

modes.

Accordingly, the simplest hydrodynamic models that allow simulating actual pro-

cesses are the HTS with random forces and linear friction.

An important problem which appeared, for example, in the theory of climate con-

sists in the determination of a possibility of signiﬁcantly different circulation processes

(t)

1,1

(t)

1,0

(t)

2,1

(t)

2,2

(t) v

2,3

(t)

1,2

(t)

2,4

(t)

(a) (b)

(t)

1,1

(t)

1,0

(t)

1,2

(t)

Figure 1.4 Diagrams of (a) three- and (b) seven-mode HTS.

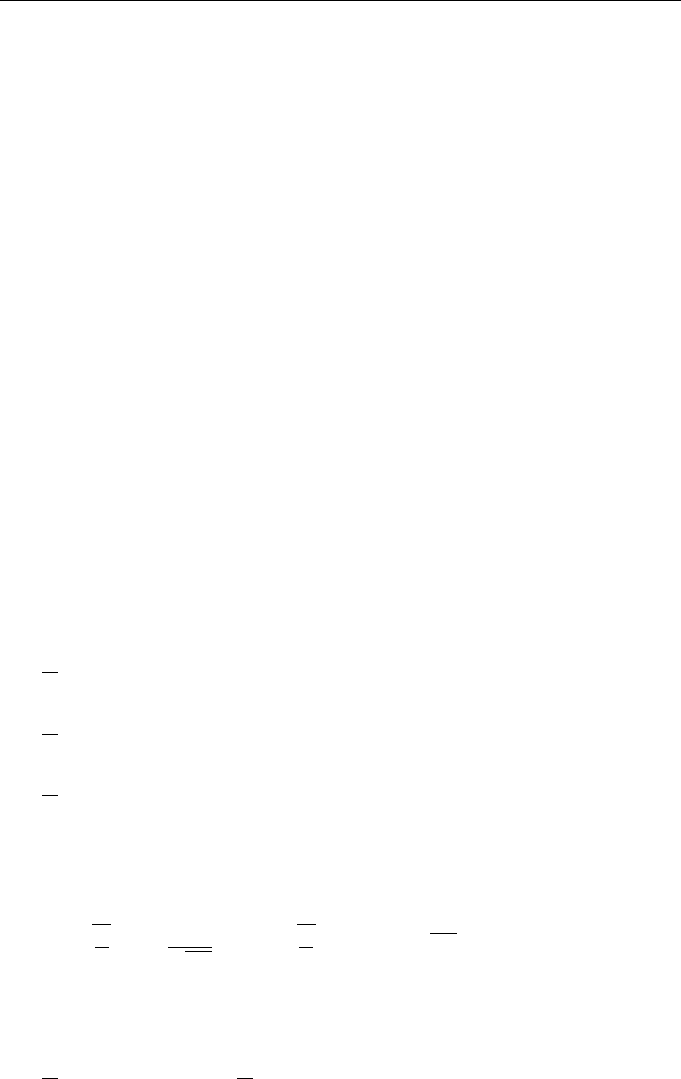
12 Lectures on Dynamics of Stochastic Systems

which occurred under the same distribution of incoming heat, i.e., the problem of the

existence of different motion regimes of a given hydrodynamic system under the same

‘external conditions’. A quite natural phenomenon that should be considered in this

context is the ‘hopping’ phenomenon that consists in switching between such regimes

of motion. Characteristic of these regimes is the fact that the duration of switching is

small in comparison with the lifetime of the corresponding regimes.

It is expedient to study these problems using the above simple models. The corres-

ponding systems of quadratically nonlinear ordinary differential equations may gene-

rally have several stable regimes, certain parameters describing external conditions

being identical. The hopping events are caused by variations of these conditions in

time and by the effect of random noises. If the system has no stable regimes, its beha-

vior can appear extremely difﬁcult and require statistical description as it is the case

in the Lorentz model [26]. In the case of availability of indifferent equilibrium states,

the system may allow quasisteady-state regimes of motion. Switching between such

regimes can be governed by the dynamic structure of the system, and system’s beha-

vior can appear ‘stochastic’ in this case, too.

In what follows, we study these hopping phenomena with the use of the simplest

hydrodynamic models.

Dynamics of a Triplet (Gyroscope)

Consider ﬁrst the case of a single stage, i.e., the triplet in the regime of forced motion

(Fig. 1.4a). With this goal, we set force f

(t) = f

= const and assume the availabil-

ity of dissipative forces acting on the stable modes of the triplet. The corresponding

equations of motion have the form

1,0

(t) = µ



1,1

(t) − v

1,2

(t)



+ f

1,1

(t) = −µv

1,0

(t)v

1,1

(t) − λv

1,1

(t),

1,2

(t) = µv

1,0

(t)v

1,2

(t) − λv

1,2

(t).

(1.17)

If f

> 0, component v

1,1

(t) vanishes with time, so that the motion of the triplet

(1.17) is described in the dimensionless variables

x =

1,0

−

√

µf

, y =

1,2

, τ =

µf

t, (1.18)

by the two-mode system

x(t) = −y

(t) + 1,

y(t) = x(t)y(t). (1.19)

Examples, Basic Problems, Peculiar Features of Solutions 13

This system has the integral of motion H

= x

(t) + y

(t) − 2 ln y(t). The change of

variables p(t) = x(t), q(t) = ln y(t) reduces the system to the Hamiltonian form

p(t) = −

∂H(p, q)

∂q

q(t) =

∂H(p, q)

∂p

with the Hamiltonian H(p, q) =

(t)

2q(t)

− q(t).

Thus, the behavior of a system with friction (1.17) under the action of a constant

external force is described in terms of the Hamiltonian system.

Stationary points (0, 1) and (0, −1) of system (1.19) are the centers. If H

−1  1,

the period T

of motion along closed trajectories around each of these singular points

is determined by the asymptotic formula (it is assumed that the sign of y(t) remains

intact during this motion)

≈

√

2π



1 +

− 1



In the opposite limiting case H

 1 (the trajectories are signiﬁcantly distant from the

mentioned centers), we obtain

≈

√

[

+ ln H

]

Supplement now the dynamic system (1.17) with the linear friction acting on com-

ponent v

1,0

(t):

1,0

(t) = µ



1,1

(t) − v

1,2

(t)



− λv

1,0

(t) + f

1,1

(t) = −µv

1,0

(t)v

1,1

(t) − λv

1,1

(t),

1,2

(t) = µv

1,0

(t)v

1,2

(t) − λv

1,2

(t).

(1.20)

Introducing again the dimensionless variables

t → t/λ, v

1,0

(t) →

(t), v

1,2

(t) →

(t), v

1,1

(t) →

(t),

we arrive at the system of equations

(t) = v

(t) − v

(t) + R,

(t) = v

(t)v

(t) − v

(t),

(t) = −v

(t)v

(t) − v

(t),

(1.21)

where quantity R =

µf

is the analog of the Reynolds number.

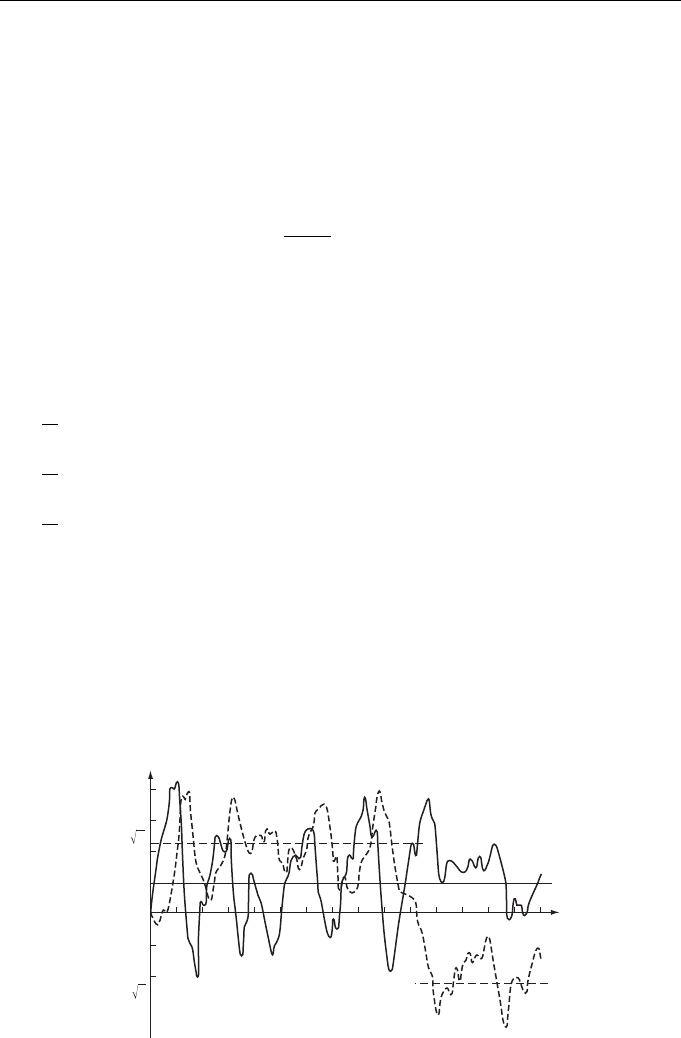
14 Lectures on Dynamics of Stochastic Systems

Dynamic system (1.21) has steady-state solutions that depend now on parameter R,

and R = R

= 1 is the critical value.

For R < 1, the system has the stable steady-state solution

= v

= 0, v

= R.

For R > 1, this solution becomes unstable with respect to small disturbances of

parameters, and the steady-state regimes

= 1, v

= 0, v

= ±

√

R − 1, (1.22)

become available. Here, we have an element of randomness because component v

can be either positive or negative, depending on the amplitude of small disturbance.

Assume now that all components of the triplet are acted on by random forces. This

means that system (1.21) is replaced with the system of equations

(t) = v

(t) − v

(t) + R + f

(t),

(t) = v

(t)v

(t) − v

(t) + f

(t),

(t) = −v

(t)v

(t) − v

(t) + f

(t).

(1.23)

This system describes the motion of a triplet (gyroscope) with the linear isotropic

friction, which is driven by the force acting on the instable mode and having both

regular (R) and random (f(t)) components. Such a situation occurs, for example, for a

liquid moving in the ellipsoidal cavity.

For R > 1, dynamic system (1.23) under the action of random disturbances will

ﬁrst reach the vicinity of one of the stable states (1.22), and then, after the lapse of cer-

tain time, it will be hoppingly set into the vicinity of the other stable state. Figure 1.5

−1

−2

10 12 14

−

Figure 1.5 Hopping phenomenon simulated from system (1.23) for R = 6 and σ = 0.1 (the

solid and dashed lines show components v

(t) and v

(t), respectively).

Examples, Basic Problems, Peculiar Features of Solutions 15

shows the results of simulations of this phenomenon for R = 6 and different realiza-

tions of random force f(t), whose components were simulated as the Gaussian random

processes. (See Sect. 8.3.3, page 200 for the statistical description of this problem.)

Thus, within the framework of the dynamics of the ﬁrst stage, hopping phenomena

can occur only due to the effect of external random forces acting on all modes.

Hopping Between Quasisteady-State Regimes

The simplest two-stage system can be represented in the form

1,0

(t) = v

1,1

(t) − v

1,2

(t) + 1,

1,1

(t) = −v

1,0

(t)v

1,1

(t) + Q



2,1

(t) − v

2,2

(t)



1,2

(t) = −v

1,0

(t)v

1,2

(t) + Q



2,3

(t) − v

2,4

(t)



2,1

(t) = −Qv

1,1

(t)v

2,1

(t),

2,2

(t) = Qv

1,1

(t)v

2,2

(t),

2,3

(t) = −Qv

1,2

(t)v

2,3

(t),

2,4

(t) = Qv

1,2

(t)v

2,4

(t),

(1.24)

where we used the dimensionless variables similar to (1.18).

Only the components v

1,0

(t), v

1,2

(t), v

2,3

(t) and v

2,4

(t) survive for f

> 0 (see

Fig. 1.6). These components satisfy the system of equations

1,0

(t) = −v

1,2

(t) + 1,

1,2

(t) = −v

1,0

(t)v

1,2

(t) + Q



2,3

(t) − v

2,4

(t)



2,3

(t) = −Qv

1,2

(t)v

2,3

(t),

2,4

(t) = Qv

1,2

(t)v

2,4

(t),

(t)

1,0

(t)

1,2

(t)

2,3

(t)

2,4

(t)

Figure 1.6 Diagram of the excited seven-mode HTS.