Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

36 Lectures on Dynamics of Stochastic Systems

system of equations (1.74) and rewrite it in the form (for simplicity, we assume that

the mean ﬂow is absent and use the zero-valued initial conditions)

r(t) = v(t),

v(t) = −λ

[

v(t) − f (t)

]

r(0) = 0, v(0) = 0,

(1.75)

the stochastic solution to which has the form

v(t) = λ

dτ e

−λ(t−τ )

f (τ ), r(t) =

dτ

1 − e

−λ(t−τ )

f(τ ).

Note that the closed linear equation of the ﬁrst order in velocity v(t) is called the

Langevin equation.

Now, we turn back to Eq. (1.71). Setting λ = 0, we arrive at the equation



∂

∂t

+ V(r, t)

∂

∂r



V(r, t) = 0, V(r, 0) = V

(r), (1.76)

called the Riemann equation. It describes free propagation of the nonlinear Riemann

wave. The solution to this equation obviously satisﬁes the transcendental equation

V(r, t) = V

(

r − tV(r, t)

)

In the special case of the one-dimensional equation



∂

∂t

+ q(x, t)

∂

∂x



q(x, t) = 0, q(x, 0) = q

(x), (1.77)

the solution can be drawn in both implicit and explicit form. This equation coincides

with Eq. (1.65) at G(t, q) = 0, U(t, q) = q(x, t).

The method of characteristics applied to Eq. (1.77) gives

q(t|x

) = q

), x(t|x

) = x

+ tq

), (1.78)

so that the solution of Eq. (1.77) can be written in the form of the transcendental equa-

tion

q(x, t) = q

(

x −tq(x, t)

)

from which follows an expression for spatial derivative

p(x, t) =

∂

∂x

q(x, t) =

)

1 + tq

)

, (1.79)

Examples, Basic Problems, Peculiar Features of Solutions 37

where

= x −tq(x, t) and q

(

)

(

)

The function p(x, t) by itself satisﬁes here the equation



∂

∂t

+ q(x, t)

∂

∂x



p(x, t) = −p

(x, t), p(x, 0) = p

(x) = q

(x). (1.80)

For completeness, we give the equation of continuity for the density ﬁeld ρ(x, t)



∂

∂t

+ q(x, t)

∂

∂x



ρ(x, t) = −p(x, t)ρ(x, t), ρ(x, 0) = ρ

(x), (1.81)

and its logarithm χ(x, t) = ln ρ(x, t)



∂

∂t

+ q(x, t)

∂

∂x



χ(x, t) = −p(x, t), χ(x, 0) = χ

(x), (1.82)

which are related to the Riemann equation (1.77). The solution to Eq. (1.77) has the

form

ρ(x, t) =

)

1 + tp

)

(x −tq(x, t))

1 + tp

(x −tq(x, t))

. (1.83)

If q

) < 0, then derivative

∂

∂x

q(x, t) and solution of Eq. (1.77) becomes discon-

tinuous. For times prior to t

, the solution is unique and representable in the form of

a quadrature. To show this fact, we calculate the variational derivative (for variational

derivative deﬁnitions and the corresponding operation rules, see Lecture 2)

δq

(

x, t

)

δq

(

)

1 + tq

(

)

(

x −tq

(

x, t

)

− x

)

Because q(x, t) =q

) and x − tq

) =x

, the argument of delta function van-

ishes at x = F(x

, t) = x

+ tq

). Consequently, we have

δq

(

x, t

)

δq

(

)

= δ(x − F(x

, t)) =

2π

∞

−∞

dk e

(

x−x

)

−iktq

(

)

We can consider this equality as the functional equation in variable q

). Then,

integrating this equation with the initial value

(

x, t

)

(

)

= 0,

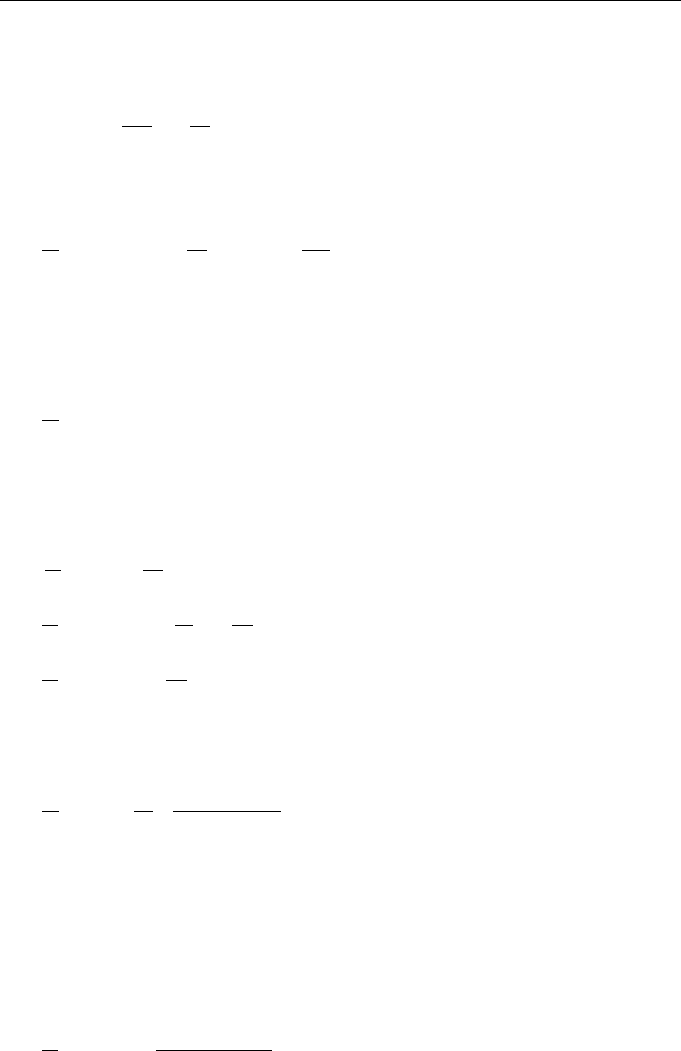
38 Lectures on Dynamics of Stochastic Systems

in the functional space, we obtain the solution of the Riemann equation in the form of

the quadrature (see e.g., [32])

(

x, t

)

2πt

∞

−∞

∞

−∞

dξe

(

x−x

)

−iktq

(ξ)

− 1

The mentioned ambiguity can be eliminated by considering the Burgers equation

∂

∂t

q(x, t) + q(x, t)

∂

∂x

q(x, t) = µ

∂

∂x

q(x, t), q(x, 0) = q

(x),

(it includes the molecular viscosity and also can be solved in quadratures) followed

by the limit process µ → 0.

In the general case, a nonlinear scalar ﬁrst-order partial differential equation can be

written in the form

∂

∂t

q(r, t) + H

(

r, t, q, p

)

= 0, q

(

r, 0

)

= q

(

)

, (1.84)

where p(r, t) = ∇q(r, t).

In terms of the Lagrangian description, this equation can be rewritten in the form

of the system of characteristic equations:

r(t|r

) =

∂

∂p

(

r, t, q, p

)

, r(0|r

) = r

;

p(t|r

) = −



∂

∂r

+ p

∂

∂q



(

r, t, q, p

)

, p(0|r

) = p

);

q(t|r

) =



∂

∂p

− 1



(

r, t, q, p

)

, q(0|r

) = q

(1.85)

Now, we supplement Eq. (1.84) with the equation for the conservative quantity

I(r, t)

∂

∂t

I(r, t) +

∂

∂r



∂H

(

r, t, q, p

)

∂p

I(r, t)



= 0, I

(

r, 0

)

= I

(

)

. (1.86)

From Eq. (1.86) follows that

drI(r, t) =

drI

(r). (1.87)

Then, in the Lagrangian description, the corresponding quantity satisﬁes the

equation

I(t|r

) = −

∂

(

r, t, q, p

)

∂r∂p

I(r, t), I

(

0|r

)

= I

(

)

Examples, Basic Problems, Peculiar Features of Solutions 39

so that the solution to Eq. (1.86) has the form

(

r, t

)

= I

(

t|r

(

t, r

))

(

t|r

)

(

t|r

)

(

t|r

)

− r

)

, (1.88)

where j

(

t|r

)

= det



∂r

(

t|r

)

/∂r



is the divergence (Jacobian).

Quantities I(t|r

) and j(t|r

) are related to each other. Indeed, substituting Eq. (1.88)

for I(r, t) in Eq. (1.87), we see that there is the evolution integral

(

t|r

)

(

)

(

t|r

)

and Eq. (1.88) assumes the form

(

r, t

)

(

)

(

t|r

)

− r

)

1.3.3 Parabolic Equation of Quasioptics (Waves in Randomly

Inhomogeneous Media)

We will describe propagation of a monochromatic wave U(t, x, R) = e

−iωt

u(x, R) in

the media with large-scale three-dimensional inhomogeneities responsible for small-

angle scattering on the base of the complex parabolic equation of quasioptics,

∂

∂x

u(x, R) =

u(x, R) +

ε(x, R)u(x, R), u(0, R) = u

(R), (1.89)

where k = ω/c is the wave number, c is the velocity of wave propagation, x-axis is

directed along the initial direction of wave propagation, vecor R denotes the coordi-

nates in the transverse plane, 1

= ∂

/∂R

, and function ε(x, R) is the deviation of

the refractive index (or dielectric permittivity) from unity. This equation was success-

fully used in many problems on wave propagation in Earth’s atmosphere and oceans

[33, 34].

Introducing the amplitude–phase representation of the waveﬁeld in Eq. (1.89) by

the formula

u(x, R) = A(x, R)e

iS(x,R)

we can write the equation for the waveﬁeld intensity

I(x, R) = u(x, R)u

∗

(x, R) = |u(x, R)|

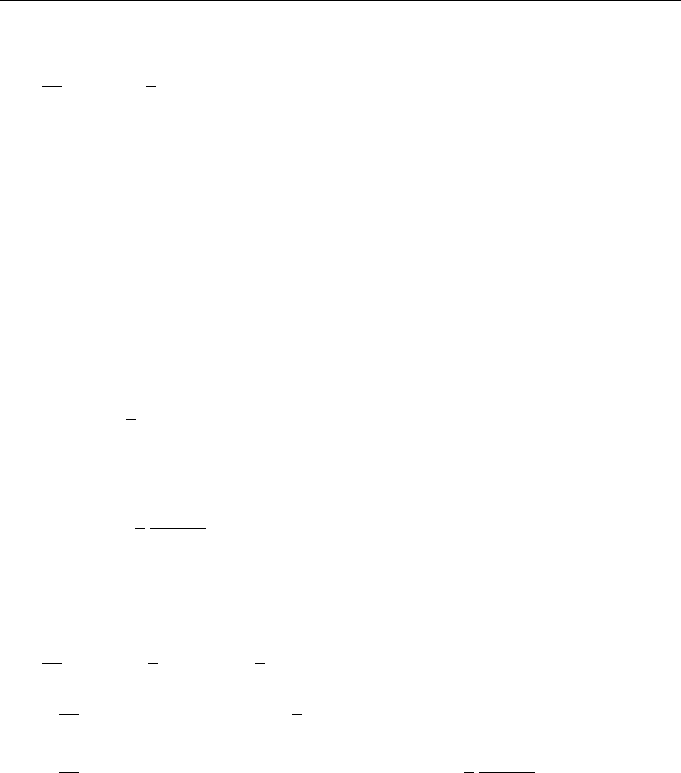
40 Lectures on Dynamics of Stochastic Systems

in the form

∂

∂x

I(x, R) +

∇

{

∇

S(x, R)I(x, R)

}

= 0, I(0, R) = I

(R). (1.90)

From this equation follows that the power of a wave in plane x = const is conserved

in the general case of arbitrary incident wave beam:

I(x, R)dR =

(R)dR.

Equation (1.90) coincides in form with Eq. (1.39). Consequently, we can treat it as

the transport equation for conservative tracer in the potential velocity ﬁeld. However,

this tracer can be considered the passive tracer only in the geometrical optics appro-

ximation, in which case the phase of the wave S(x, R), the transverse gradient of the

phase

p(x, R) =

∇

S(x, R),

and the matrix of the phase second derivatives

(x, R) =

∂

∂R

S(x, R)

characterizing the curvature of the phase front S(x, R) = const satisfy the closed

system of equations

∂

∂x

S(x, R) +

(x, R) =

ε(x, R),



∂

∂x

+ p(x, R)∇



p(x, R) =

∇

ε(x, R),



∂

∂x

+ p(x, R)∇



(x, R) + u

(x, R)u

(x, R) =

∂

∂R

ε(x, R).

(1.91)

In the general case, i.e., with the inclusion of diffraction effects, this tracer is the

active tracer.

According to the material of Sect. 1.3.1, realizations of intensity must show the

cluster behavior, which manifests itself in the appearance of caustic structures.

An example demonstrating the appearance of the waveﬁeld caustic structures is

given in Fig. 1.15, which is a fragment of the photo on the back of the cover – the

ﬂyleaf – of book [33] that shows the transverse section of a laser beam in turbulent

medium (laboratory measurements).

A photo of the pool in Fig. 1.16 also shows the prominent caustic structure of the

waveﬁeld on the pool bottom. Such structures appear due to light refraction and reﬂec-

tion by rough water surface, which corresponds to scattering by the so-called phase

screen.

Examples, Basic Problems, Peculiar Features of Solutions 41

Figure 1.15 Transverse section of a laser beam in turbulent medium.

Figure 1.16 Caustics in a pool.

Note that Eq. (1.89) with parameter x concidered as time coincides in form with the

Schr

odinger equation. In a similar way, the nonlinear parabolic equation describing

self-action of a harmonic wave ﬁeld in multidimensional random media,

∂

∂x

u(x, R) =

u(x, R) +

ε(x, R;I(x, R))u(x, R), u(0, R) = u

(R),

coincides in form with the nonlinear Schr

odinger equation. Consequently, clustering

of wave ﬁeld energy must occur in this case too, because Eq. (1.90) is formally inde-

pendent of the shape of function ε(x, R;I(x, R)).

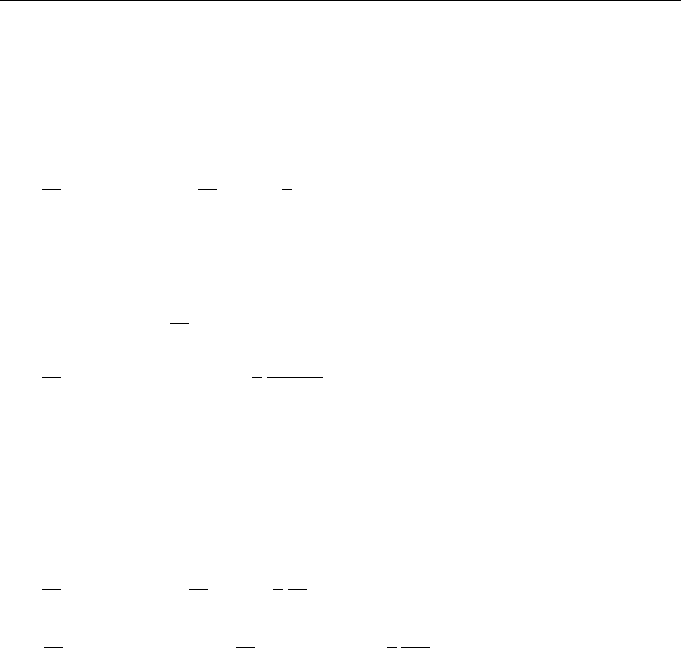
42 Lectures on Dynamics of Stochastic Systems

Consider now geometrical optics approximation (1.91) for parabolic equation

(1.89). In this approximation, the equation for the wave phase is the Hamilton–Jacobi

equation and the equation for the transverse gradient of the phase (1.91) is the closed

quasilinear ﬁrst-order partial differential equation, and we can solve it by the method

of characteristics. Equations for the characteristic curves (rays) have the form

R(x) = p(x),

p(x) =

∇

ε(x, R), (1.92)

and the waveﬁeld intensity and matrix of the phase second derivatives along the cha-

racteristic curves will satisfy the equations

I(x) = −I(x)u

(x),

(x) + u

(x)u

(x) =

∂

∂R

ε(x, R).

(1.93)

Equations (1.92) coincide in appearance with the equations for a particle under

random external forces in the absence of friction (1.12) and form the system of the

Hamilton equations.

In the two-dimensional case (R = y), Eqs. (1.92), (1.93) become signiﬁcantly sim-

pler and assume the form

y(x) = p(x),

p(x) =

∂

∂y

ε(x, y),

I(x) = −I(x)u(x),

u(x) + u

(x) =

∂

∂y

ε(x, y).

(1.94)

The last equation for u(x) in (1.94) is similar to Eq. (1.29) whose solution shows the

singular behavior. The only difference between these equations consists in the random

term that has now a more complicated structure. Nevertheless, it is quite clear that

solutions to stochastic problem (1.94) will show the blow-up behavior; namely, func-

tion u(x) will reach minus inﬁnity and intensity will reach plus inﬁnity at a ﬁnite dis-

tance. Such a behavior of a waveﬁeld in randomly inhomogeneous media corresponds

to random focusing, i.e., to the formation of caustics, which means the appearance of

points of multivaluedness (and discontinuity) in the solutions of quasilinear equation

(1.91) for the transverse gradient of the waveﬁeld phase.

1.3.4 Navier–Stokes Equation: Random Forces in

Hydrodynamic Theory of Turbulence

Consider now the turbulent motion model that assumes the presence of external forces

f(r, t) acting on the liquid. Such a model is evidently only imaginary, because there

are no actual analogues for these forces. However, assuming that forces f (r, t) on

average ensure an appreciable energy income only to large-scale velocity components,

we can expect that, within the concepts of the theory of local isotropic turbulence, the

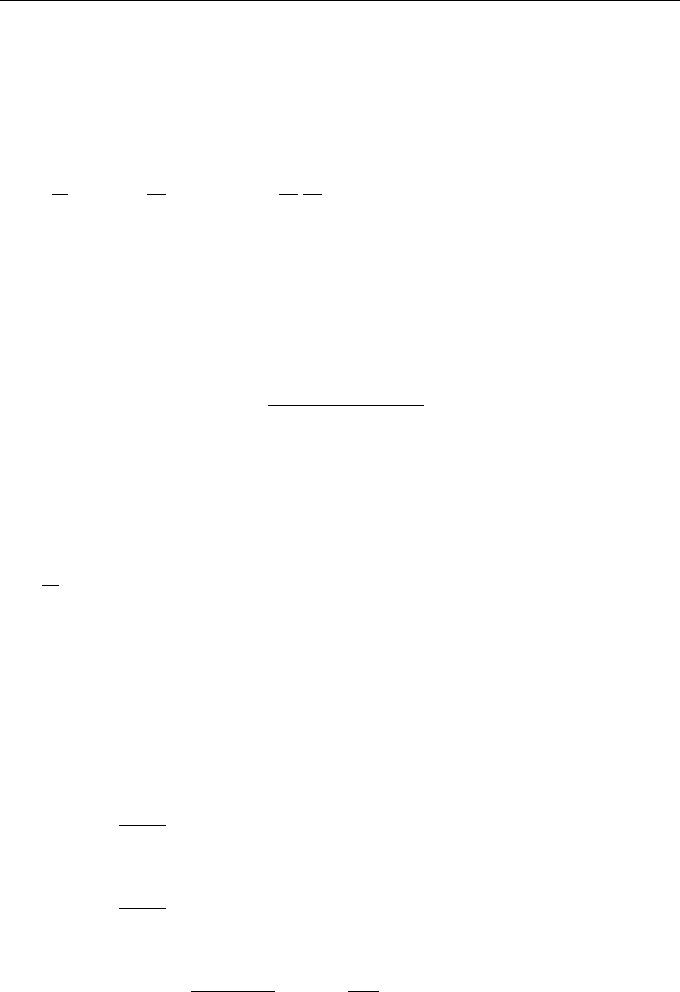
Examples, Basic Problems, Peculiar Features of Solutions 43

imaginary nature of ﬁeld f(r, t) will only slightly affect statistical properties of small-

scale turbulent components [35]. Consequently, this model is quite appropriate for

describing small-scale properties of turbulence.

Motion of an incompressible liquid under external forces is governed by the

Navier–Stokes equation



∂

∂t

+ u(r, t)

∂

∂r



u(r, t) = −

∂

∂r

p(r, t) + ν1u(r, t) + f (r, t),

div u(r, t) = 0, div f (r, t) = 0.

(1.95)

Here, ρ

is the density of the liquid, ν is the kinematic viscosity, and pressure

ﬁeld p(x, t) is expressed in terms of the velocity ﬁeld at the same instant by the

relationship

p(r, t) = −ρ

−1



r, r



∂



, t)u

, t)



∂r

, (1.96)

where 1

−1

(r, r

) is the integral operator inverse to the Laplace operator (repeated

indices assume summation).

Note that the linearized equation (1.95)

∂

∂t

u(r, t) = ν1u(r, t) + f (r, t), u(r, 0) = 0, (1.97)

describes the problem on turbulence degeneration for t → ∞. The solution to this

problem can be drawn in an explicit form:

u(r, t) =

dτ e

ν(t−τ )1

f (r, τ ) =

dτ e

ντ 1

δ(r − r

)f (r

, t − τ )

(2π)

dτ e

ντ 1

dq e

iq(r−r

)

f (r

, t − τ )

(2π)

dτ

dq e

−ντ q

iqr

f (r − r

, t − τ )

dτ

(4πντ )

3/2

exp



−

4ντ



f (r − r

, t − τ ). (1.98)

The linear equation (1.97) is an extension of the Langevin equation in velocity (1.75),

page 36 to random ﬁelds.

44 Lectures on Dynamics of Stochastic Systems

Neglecting the effect of viscosity and external random forces in Eq. (1.95), we

arrive at the equation

∂

∂t

u(r, t) +

(

u(r, t) · ∇

)

u(r, t) = −

∇p(r, t) (1.99)

that describes dynamics of perfect liquid and is called the Euler equation. Using

Eq. (1.58), page 29, this equation can be rewritten in terms of the velocity ﬁeld vortex

ω = curl u(r, t) as

∂

∂t

ω(r, t) = curl

[

u(r, t) × ω(r, t)

]

, ω(r, 0) = ω

(r), (1.100)



∂

∂t

∂

∂r

u(r, t)



ω(r, t) =



ω(r, t) ·

∂

∂r



ω(r, t), ω(r, 0) = ω

(r). (1.101)

These equations coincide with Eqs. (1.52) and (1.59), pages 28 and 30, and appeared

in the problem on the diffusion of magnetic ﬁeld.

However, this coincidence is only formal, because different boundary conditions to

these problems results in drastically different behaviors of ﬁelds ω(r, t) and H(r, t) as

functions of the velocity ﬁeld u(r, t).

If we substitute Eq. (1.96) in Eq. (1.95) to exclude the pressure ﬁeld, then we obtain

in the three-dimensional case that the Fourier transform of the velocity ﬁeld with res-

pect to spatial coordinates

(k, t) =

dru

(r, t)e

−ikr

, u

(r, t) =

(2π)

dkbu

(k, t)e

ikr

(bu

∗

(k, t) =bu

(−k, t)) satisﬁes the nonlinear integro-differential equation

∂

∂t

(

k, t

)

αβ

(

, k

)

(

, t

)

(

, t

)

− νk

(

k, t

)

(

k, t

)

, (1.102)

where

αβ

(

, k

)

(

2π

)



iβ

(

)

+ k

iα

(

)



δ(k

+ k

− k),

(

)

= δ

−

(i, α, β = 1, 2, 3),

and

f (k, t) is the spatial Fourier harmonics of external forces,

f (k, t) =

dr f(r, t)e

−ikr

, f (r, t) =

(2π)

f (k, t)e

ikr

A speciﬁc feature of the three-dimensional hydrodynamic motions consists in the

fact that the absence of external forces and viscosity-driven effects is sufﬁcient for

energy conservation.

Examples, Basic Problems, Peculiar Features of Solutions 45

It appears convenient to describe the stationary turbulence in terms of the space-

time Fourier harmonics of the velocity ﬁeld

(K) =

∞

−∞

dtu

(x, t)e

−i(kx+ωt)

(x, t) =

(2π)

∞

−∞

dωbu

(K)e

i(kx+ωt)

where K is the four-dimensional wave vector {k, ω} and ﬁeld bu

∗

(K) = bu

(−K)

because ﬁeld u

(r, t) is real. In this case, we obtain the equation for component bu

(K)

by performing the Fourier transformation of Eq. (1.102) with respect to time:

(iω + νk

)bu

(

)

αβ

(

, K

)

(

)

(

)

(

)

(1.103)

where

αβ

(

, K

)

2π

αβ

(

, k

)

δ(ω

+ ω

− ω),

and

(K) are the space-time Fourier harmonics of external forces. The obtained

Eq. (1.103) is now the integral (and not integro-differential) nonlinear equation.

Plane Motion Under the Action of a Periodic Force

Consider now the two-dimensional motion of an incompressible viscous liquid

U(r, t) = {u(r, t), v(r, t)} in plane r = {x, y} under the action of a spatially peri-

odic force directed along the x-axis f

(r, t) = γ sin py (γ > 0). Such a ﬂow is usually

called the Kolmogorov ﬂow (stream). The corresponding motion is described by the

system of equations

∂u

∂t

∂u

∂x

∂uv

∂y

= −

∂P

∂x

+ ν1u +γ sin py,

∂v

∂t

∂uv

∂x

∂v

∂y

= −

∂P

∂y

+ ν1v,

∂u

∂x

∂v

∂y

= 0,

(1.104)

where P(r, t) is the pressure, ρ is the density, and ν is the kinematic viscosity.

The system of the Navier–Stokes and continuity equations (1.104) has the steady-

state solution that corresponds to the laminar ﬂow at constant pressure along the x-axis

and has the following form

s-s

(r) =

νp

sin py, v

s-s

(r) = 0, P

s-s

(r) = const. (1.105)