Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

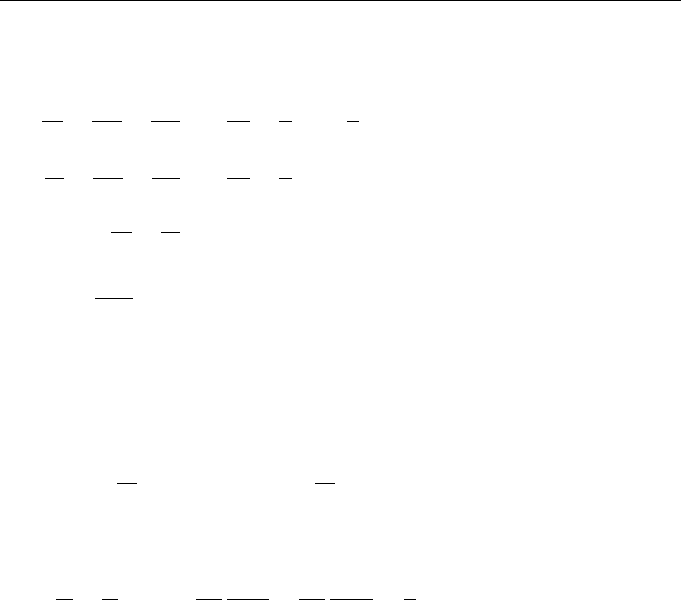
46 Lectures on Dynamics of Stochastic Systems

Introducing scales of length p

−1

, velocity p

−2

−1

γ , and time pνγ

−1

and using dimen-

sionless variables, we reduce system (1.104) to the form

∂u

∂t

∂u

∂x

∂uv

∂y

= −

∂P

∂x

1u +

sin y,

∂v

∂t

∂uv

∂x

∂v

∂y

= −

∂P

∂y

1v,

∂u

∂x

∂v

∂y

= 0,

(1.106)

where R =

is the Reynolds number. In these variables, the steady-state solution

has the form

s-s

(r) = sin y, v

s-s

(r) = 0, P

s-s

(r) = const.

Introducing ﬂow function ψ(r, t) by the relationship

u(r, t) =

∂

∂y

ψ(r, t), v(r, t) = −

∂

∂x

ψ(r, t),

we obtain that it satisﬁes the equation



∂

∂t

−



1ψ −

∂ψ

∂x

∂1ψ

∂y

∂ψ

∂y

∂1ψ

∂x

cos y, (1.107)

and

s-s

(r) = −cos y.

It was shown [43, 44] that, in the linear problem formulation, the steady-state solu-

tion (1.105) corresponding to the laminar ﬂow is unstable with respect to small dis-

turbances for certain values of parameter R. These disturbances rapidly increase in

time getting the energy from the ﬂow (1.105); this causes the Reynolds stresses des-

cribed by the nonlinear terms in Eq. (1.107) to increase, which results in decreasing

the amplitude of laminar ﬂow until certain new steady-state ﬂow (called usually the

secondary ﬂow) is formed.

We represent the hydrodynamic ﬁelds in the form

u(r, t) = U(y, t) +eu(r, t), v(r, t) =ev(r, t),

P(r, t) = P

P(r, t), ψ(r, t) = 9(y, t) +

ψ(r, t).

Here, U(y, t) is the new proﬁle of the steady-state ﬂow to be determined together with

the Reynolds stresses and the tilde denotes the corresponding ultimate disturbances.

Abiding by the cited works, we will consider disturbances harmonic in variable x with

Examples, Basic Problems, Peculiar Features of Solutions 47

wavelength 2π/α (α > 0). The new ﬂow proﬁle U(y, t) is the result of averaging with

respect to x over distances of about a wavelength.

One can easily see that, for α ≥ 1, the laminar ﬂow (1.105) is unique and stable for

all R [44] and instability can appear only for disturbances with α < 1.

According to the linear stability theory, we will consider ﬁrst the nonlinear inter-

action only between the ﬁrst harmonic of disturbances and the mean ﬂow and neglect

the generation of higher harmonics and their mutual interactions and interaction with

the mean ﬂow.

We represent all disturbances in the form

eϕ(r, t) = ϕ

(1)

(y, t)e

iαx

+ ϕ

(−1)

(y, t)e

−iαx



eϕ(r, t) =eu(r, t), ev(r, t),

P(r, t),

ψ(r, t)



where quantity ϕ

(−1)

(y, t) is the complex conjugated of ϕ

(1)

(y, t). Then, using this rep-

resentation in system (1.106) and eliminating quantities

P(r, t) and eu(r, t), we obtain

the system of equations in mean ﬂow U(y, t) and disturbances v

(1)

(y, t) [24, 25]:

∂

∂t

U +

(−1)

∂

(1)

∂y

− v

(1)

∂

(−1)

∂y

∂

∂y

sin y,



∂

∂t

−



(1)

+ iα



U1v

(1)

− v

(1)

∂

∂y



= 0.

(1.108)

The second equation in system (1.108) is the known Orr–Sommerfeld equation.

A similar system can be derived for the ﬂow function.

To examine the stability of the laminar regime (1.105), we set

U(y) = sin y

in the second equation of system (1.108) to obtain



∂

∂t

−



(1)

(y, t) + iα sin y[1 + 1]v

(1)

(y, t) = 0. (1.109)

Representing disturbances v

(1)

(y, t) in the form

(1)

(y, t) =

∞

n=−∞

(1)

σ t+iny

, (1.110)

and substituting this representation in Eq. (1.109), we arrive at the recurrent system in

quantities v

(1)



+ n





σ +

+ n



(1)

+ v

(1)

n−1

− 1 + (n − 1)

− v

(1)

n+1

− 1 + (n + 1)

= 0, n = −∞, . . . , +∞. (1.111)

48 Lectures on Dynamics of Stochastic Systems

The analysis of system (1.111) showed [43, 44] that, under certain restrictions on

wave number α and Reynolds number R, positive values of parameter σ can exist, i.e.,

the solutions are unstable. The corresponding dispersion equation in σ has the form

of an inﬁnite continued fraction, and the critical Reynolds number is R

√

2 for

α → 0. In other words, long-wave disturbances along the applied force appear to be

most unstable. For this reason, we can consider parameter α as a small parameter of

the problem at hand and integrate the Orr–Sommerfeld equation asymptotically. We

will not dwell on details of this solution. Note only that the components of eigenvec-

tor



(1)



of problem (1.111) have different orders of magnitude in parameter α. For

example, all components of vector



(1)



with n = ±2, ±3, . . . will have an order

of α

at least. As a result, we can conﬁne ourselves to the most signiﬁcant harmonics

with n = 0, ±1, which, in essence, is equivalent to the Galerkin method with the

trigonometric coordinate functions. In this case,

U(y, t) = U(t) sin y,

and the equation in v

(1)

assumes the form



∂

∂t

−



(1)

(y, t) + iαU(t) sin y[1 + 1]v

(1)

(y, t) = 0.

Substituting the expansion

(1)

(y, t) =

n=−1

(1)

(t)e

iny

in Eqs. (1.108), we obtain that functions

U(t), z

(t) = v

(1)

(t), z

(t) = v

(1)

(t) + v

(1)

−1

(t),

−

(t) =

(1)

(t) − v

(1)

−1

(t)

satisfy the system of equations [24, 45]





U(t) =

−

(t)z

−

(t),





(t) = αU(t)z

−

(t),





−

(t) =

U(t)z

(t),





(t) = 0.

(1.112)

Examples, Basic Problems, Peculiar Features of Solutions 49

Equation in quantity z

(t) is independent of other equations; as a consequence, the

corresponding disturbances can only decay with time. Three remaining equations form

the simplest three-component hydrodynamic-type system (see Sect. 1.1.3, page 10).

As was mentioned earlier, this system is equivalent to the dynamic system describing

the motion of a gyroscope with anisotropic friction under the action of an external

moment of force relative to the unstable axis. An analysis of system (1.112) shows

that, for R < R

√

2, it yields the laminar regime with U = 1, z

= 0. For R >

√

this regime becomes unstable, and new regime (the secondary ﬂow) is formed that

corresponds to the mean ﬂow proﬁle and steady-state Reynolds stresses

U =

√

−

R −

√

, z

= 0,

(1)

R −

√

, v

(1)

√

(1)

, α  1, R ≥

√

Turning back to the dimensional quantities, we obtain

U(y) =

√

2υp sin py,

euev

= −

R −

√

cos py. (1.113)

Note that the amplitude of the steady-state mean ﬂow is independent of the ampli-

tude of exciting force. Moreover, quantity v

(1)

can be both positive and negative,

depending on the signs of the amplitudes of small initial disturbances.

Flow function of the steady-state ﬂow has the form

(x, y) = −

√

cos y −

(1)

√

2α sin y cos αx + sin αx

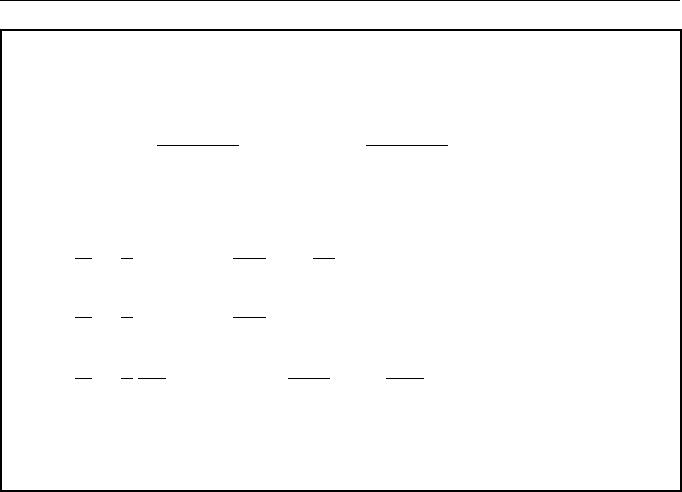
Figure 1.17 shows the current lines

α cos y +

√

2α sin y cos αx + sin αx = C

of ﬂow (1.113) at R = 2R

= 2

√

2 (v

(1)

> 0).

In addition, Fig. 1.17 shows schematically the proﬁle of the mean ﬂow. As distinct

from the laminar solution, systems of spatially periodic vortices appear here, and the

tilt of longer axes of these vortices is determined by the sign of the derivative of the

mean ﬂow proﬁle with respect to y.

Flow (1.113) was derived under the assumption that the nonlinear interactions bet-

ween different harmonics of the disturbance are insigniﬁcant in comparison with their

interactions with the mean ﬂow. This assumption will hold if ﬂow (1.113) is, in turn,

stable with respect to small disturbances. The corresponding stability analysis can be

carried out by the standard procedure, i.e., by linearizing the equation for ﬂow func-

tion (1.107) relative to ﬂow (1.113) [45]. The analysis shows that ﬂow (1.113) is stable

50 Lectures on Dynamics of Stochastic Systems

−

C = 0

C = 1 + α

C = 1 − α

αx

−π

2√ 3α

4√ α

2√ 3α 2√ 3α

2√ 2α

4√ α

2√ 2α

C = −1

C = 0

3π

−

Figure 1.17 Mean velocity and current lines of the secondary ﬂow at R = 2R

= 2

√

(1)

> 0).

if we restrict ourselves to the harmonics of the types same as in solution (1.113). How-

ever, the solution appears to be unstable with respect to small-scale disturbances. In

this case, the nonlinear interaction of inﬁnitely small disturbances governs the motion

along with the interaction of the disturbances with the mean ﬂow. Moreover, we can-

not here content ourselves with a ﬁnite number of harmonics in x-coordinate and need

to consider the inﬁnite series. As regards the harmonics in y-coordinate, we, as earlier,

can limit the consideration to the harmonics with n = 0, ±1.

Problem

Problem 1.1

Derive the system of equations which takes into account the whole inﬁnite series

of harmonics in x-coordinate and extends the system of gyroscopic-type equa-

tions (1.112) to the inﬁnite-dimensional case.

Solution Represent the ﬂow function in the form

ψ(x, y, t) = ψ

−1

(x, t)e

−iy

+ ψ

(x, t) + ψ

(x, t)e

(ψ

∗

(x, t) = ψ

−1

(x, t)),

(1.114)

where ψ

(x, t) are the periodic functions in x-coordinate with a period 2π/α.

Substituting Eq. (1.114) in Eq. (1.107), neglecting the terms of order α

Examples, Basic Problems, Peculiar Features of Solutions 51

interactions of harmonics and the terms of order α

in the dissipative terms of

harmonics ψ

±1

, and introducing new functions

(x, t) =

−1

+ ψ

, ψ

−

(x, t) =

−1

− ψ

we obtain the system of equations



∂

∂t



− ψ

−

∂ψ

∂x

= −



∂

∂t



−

+ ψ

∂ψ

∂x

= 0,



∂

∂t

−

∂

∂x



+ 2



−

∂ψ+

∂x

− ψ

∂ψ

−

∂x



= 0.

Its characteristic feature consists in the absence of steady-state solutions periodic

in x-coordinate (except the solution corresponding to the laminar ﬂow).

This page intentionally left blank

Lecture 2

Solution Dependence on Problem Type,

Medium Parameters, and Initial Data

Below, we consider a number of dynamic systems described by both ordinary and

partial differential equations. Many applications concerning research of statistical

characteristics of the solutions to these equations require the knowledge of solution

dependence (generally, in the functional form) on the medium parameters appearing

in the equation as coefﬁcients and initial values. Some properties appear common to

all such dependencies, and two of them are of special interest in the context of sta-

tistical descriptions. We illustrate these dependencies by the example of the simplest

problem, namely, the system of ordinary differential equations (1.1) that describes par-

ticle dynamics under random velocity ﬁeld and which we reformulate in the form of

the nonlinear integral equation

r(t) = r

dτ U(r(τ ), τ ). (2.1)

The solution to Eq. (2.1) functionally depends on vector ﬁeld U(r

, τ ) and initial

values r

, t

2.1 Functional Representation of Problem Solution

2.1.1 Variational (Functional) Derivatives

Recall ﬁrst the general deﬁnition of a functional. One says that a functional is given

if a rule is ﬁxed that associates a number to every function from a certain function

family. Below, we give some examples of functionals:

(a) F[ϕ(τ )] =

dτ a(τ )ϕ(τ),

Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00002-7

54 Lectures on Dynamics of Stochastic Systems

ϕ (τ)

ϕ (τ) + δϕ(τ)

Δτ

t −

Δτ

t +

Figure 2.1 To deﬁnition of variational derivative.

where a(t) is the given (ﬁxed) function and limits t

and t

can be both ﬁnite and

inﬁnite. This is the linear functional.

(b) F[ϕ(τ )] =

dτ

B(τ

, τ

)ϕ(τ

where B(t

, t

) is the given (ﬁxed) function. This is the quadratic functional.

(

8[ϕ(τ )]

)

where f (x) is the given function and quantity 8[ϕ(τ )] is the functional.

Estimate the difference between the values of a functional calculated for functions

ϕ(τ ) and ϕ(τ ) + δϕ(τ ) for t −

1τ

< τ < t +

1τ

(see Fig. 2.1).

The variation of a functional is deﬁned as the linear (in δϕ(τ )) portion of the

difference

δF[ϕ(τ)] =

{

[

ϕ(τ ) + δϕ(τ )

]

− F[ϕ(τ )]

}

The limit

δF[ϕ(τ)]

δϕ(t)dt

= lim

1τ →0

δF[ϕ(τ)]

1τ

dτ δϕ(τ )

, (2.2)

is called the variational (or functional) derivative (see, e.g., [35]).

For short, we will use notation

δF[ϕ(τ)]

δϕ(t)

instead of

δF[ϕ(τ)]

δϕ(t)dt

Note that, if we use function δϕ(τ ) = αδ(τ ), where δ(τ) is the Dirac delta function,

then Eq. (2.2) can be represented in the form of the ordinary derivative

δF[ϕ(τ)]

δϕ(t)

= lim

α→0

dα

F[ϕ(τ ) + αδ(τ − t)].

Solution Dependence on Problem Type, Medium Parameters, and Initial Data 55

The variational derivative of functional F[ϕ(τ )] is again the functional of ϕ(τ),

which depends additionally on point t as a parameter. As a result, this variational

derivative will have two types of derivatives; one can differentiate it in the ordinary

sense with respect to parameter t and in the functional sense with respect to ϕ(τ ) at

point τ = t

, thus obtaining the second variational derivative of the initial functional

F[ϕ(τ )]

δϕ(t

)δϕ(t)

δϕ(t

)



δF[ϕ(τ)]

δϕ(t)



The second variational derivative will now be the functional of ϕ(τ ) dependent on two

points t and t

, and so forth.

Determine the variational derivatives of functionals (a), (b), and (c).

In case (a), we have

δF[ϕ(τ)] = F[ϕ(τ) + δϕ(τ)] −F[ϕ(τ)] =

1τ

t−

1τ

dτ a(τ )δϕ(τ).

If function a(t) is continuous on segment 1τ, then, by the average theorem,

δF[ϕ(τ)] = a(t

)

1τ

dτ δϕ(τ ),

where point t

belongs to segment



t −

1τ

, t +

1τ



. Consequently,

δF[ϕ(τ)]

δϕ(t)

= lim

1τ →0

a(t

) = a(t). (2.3)

In case (b), we obtain similarly

δF[ϕ(τ)]

δϕ(t)

dτ

[

B(τ,t)+B(t, τ )

]

ϕ(τ ) (t

< t < t

Note that function B(τ

, τ

) can always be assumed a symmetric function of its argu-

ments here.

In case (c), we have

F[ϕ(τ ) + δϕ(τ )] = f

(

8[ϕ(τ )]

)

∂f

(

8[ϕ(τ )]

)

∂8

δ8[ϕ(τ)] + ···

= F[ϕ(τ )] +

∂f

(

8[ϕ(τ )]

)

∂8

δ8[ϕ(τ)] + ···

and, consequently,

δϕ(t)

(

8[ϕ(τ )]

)

∂f

(

8[ϕ(τ )]

)

∂8

δϕ(t)

8[ϕ(τ )]. (2.4)