Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.

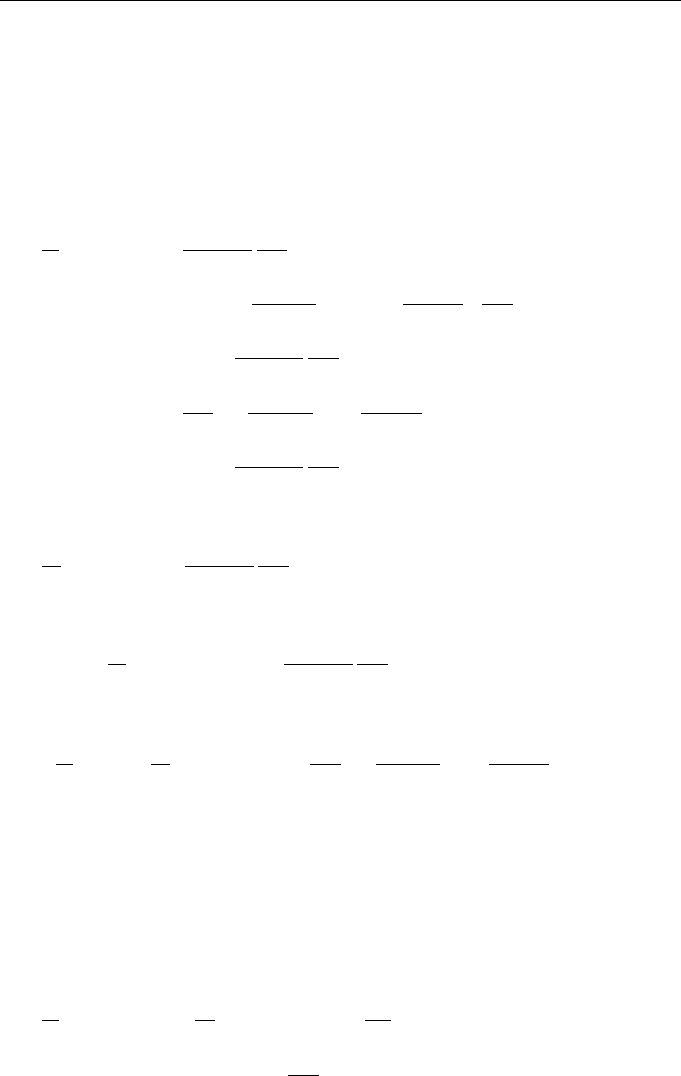
76 Lectures on Dynamics of Stochastic Systems
Magnetic Field Diffusion Under Random Velocity Field
Let us introduce the indicator function of magnetic field H(r, t),
ϕ(r, t; H) = δ(H(r, t) − H).
Differentiating this function with respect to time with the use of dynamic
equation (1.59), page 30, and probing property of the delta function, we arrive at the
equation
∂
∂t
ϕ(r, t; H) = −
∂H
i
(r, t)
∂t
∂
∂H
i
ϕ(r, t; H)
= −
H(r, t)
∂u
i
(r, t)
∂r
− H
i
(r, t)
∂u(r, t)
∂r
∂
∂H
i
ϕ(r, t; H)
+ u(r, t)
∂H
i
(r, t)
∂r
∂
∂H
i
ϕ(r, t; H)
= −
∂
∂H
i
H
∂u
i
(r, t)
∂r
− H
i
∂u(r, t)
∂r
ϕ(r, t; H)
+ u(r, t)
∂H
i
(r, t)
∂r
∂
∂H
i
ϕ(r, t; H),
which is unclosed because of the last term. However, since
∂
∂r
ϕ(r, t; H) = −
∂H
i
(r, t)
∂r
∂
∂H
i
δ(H(r, t) − H)
and, hence,
−u(r, t)
∂
∂r
ϕ(r, t; H) = u(r, t )
∂H
i
(r, t)
∂r
∂
∂H
i
δ(H(r, t) − H),
we obtain the desired closed Liouville equation [16]
∂
∂t
+ u(r, t)
∂
∂r
ϕ(r, t; H) = −
∂
∂H
i
H
∂u
i
(r, t)
∂r
− H
i
∂u(r, t)
∂r
ϕ(r, t; H)
(3.26)
with the initial condition
ϕ(r, 0; H) = δ(H
0
(r) − H).
Note that, in the case of velocity field described by the simplest model (1.15),
page 10, u(x, t) = v(t)f (x) (x is the dimensionless variable), the Liouville equation
(3.26) with homogeneous initial conditions becomes the equation
∂
∂t
ϕ(x, t; H) =
−
∂
∂x
f (x) + f
0
(x)
1 +
∂
∂H
H
v
x
(t)ϕ(x, t; H)
− f
0
(x)H
x0
v
i
(t)
∂
∂H
i
ϕ(x, t; H) (3.27)
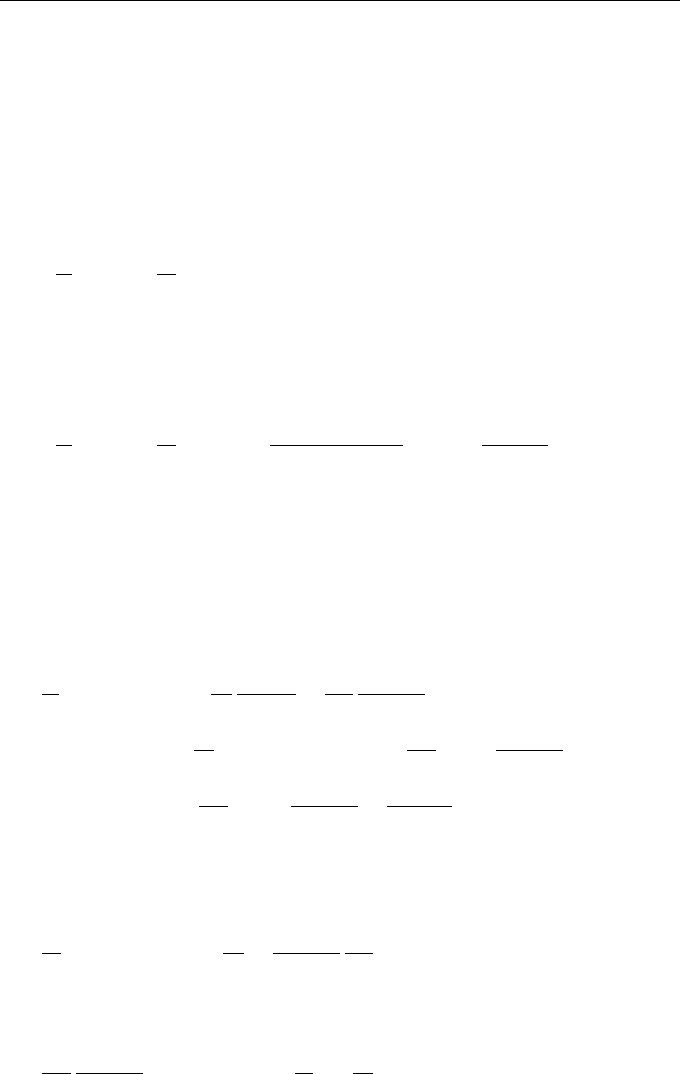
Indicator Function and Liouville Equation 77
with the initial condition
ϕ(x, 0; H) = δ(H
0
− H).
3.2.2 Quasilinear Equations
Consider now the simplest quasilinear equation for scalar quantity q(r, t) (1.65),
page 33,
∂
∂t
+ U(t, q)
∂
∂r
q(r, t) = Q
(
t, q
)
, q(r, 0) = q
0
(r). (3.28)
In this case, an attempt of deriving a closed equation for the indicator function
ϕ(r, t; q) = δ(q(r, t)− q) on the analogy of the linear problem will fail. Here, we must
supplement Eq. (3.28) with (1.66), page 33, for the gradient field p(r, t) = ∇q(r, t)
∂
∂t
+ U(t, q)
∂
∂r
p(r, t) +
∂
{
U(t, q)p(r, t)
}
∂q
p(r, t) =
∂Q(t, q)
∂q
p(r, t) (3.29)
and consider the extended indicator function
ϕ(r, t; q, p) = δ(q(r, t) − q)δ(p(r, t) − p). (3.30)
Differentiating Eq. (3.30) with respect to time and using Eqs. (3.28) and (3.29), we
obtain the equation
∂
∂t
ϕ(r, t; q, p) = −
∂
∂q
∂q(r, t)
∂t
+
∂
∂p
k
∂p
k
(r, t)
∂t
ϕ(r, t; q, p)
=
∂
∂q
[
pU(t, q) − Q(t, q)
]
+
∂
∂p
k
U(t, q)
∂p
k
(r, t)
∂r
ϕ(r, t; q, p)
+
∂
∂p
k
p
k
p
∂U (t, q)
∂q
−
∂Q(t, q)
∂q
ϕ(r, t; q, p), (3.31)
which is unclosed, however, because of the term ∂p
k
(r, t)/∂r in the right-hand side.
Differentiating function (3.30) with respect to r, we obtain the equality
∂
∂r
ϕ(r, t; q, p) = −
p
∂
∂q
+
∂p
k
(r, t)
∂r
∂
∂p
k
ϕ(r, t; q, p), (3.32)
from which follows that
∂
∂p
k
∂p
k
(r, t)
∂r
ϕ(r, t; q, p) = −
∂
∂r
+ p
∂
∂q
ϕ(r, t; q, p).

78 Lectures on Dynamics of Stochastic Systems
Consequently, Eq. (3.31) can be rewritten in the closed form
∂
∂t
+ U(t, q)
∂
∂r
ϕ(r, t; q, p) =
p
∂U (t, q)
∂q
−
∂
∂q
Q(t, q)
ϕ(r, t; q, p)
+
∂
∂p
k
p
k
p
∂U (t, q)
∂q
−
∂Q(t, q)
∂q
ϕ(r, t; q, p),
(3.33)
which is just the desired Liouville equation for the quasilinear equation (3.28) in the
extended phase space {q, p} with the initial value
ϕ(r, 0; q, p) = δ(q
0
(r) − q)δ(p
0
(r) − p).
Note that the equation of continuity for conserved quantity I(r, t)
∂
∂t
I(r, t) +
∂
∂r
{
U(t, q)I(r, t)
}
= 0, I(r, 0) = I
0
(r)
can be combined with Eqs. (3.28), (3.29). In this case, the indicator function has the
form
ϕ(r, t; q, p, I) = δ(q(r, t) − q)δ(p(r, t) − p)δ(I(r, t) − I)
and derivation of the closed equation for this function appears possible in space
{q, p, I}, which follows from the fact that, in the Lagrangian description, quantity
inverse to I(r, t) coincides with the divergence.
Note that the Liouville equation in indicator function
ϕ(x, t; q, p, χ) = δ
(
q(x, t) − u
)
δ
(
p(x, t) − p
)
δ
(
χ(x, t) − χ
)
in the case of the one-dimensional Riemann equation (1.77), page 36, in function
q(x, t) complemented with the equations for the gradient field p(x, t) =
∂q(x, t)
∂x
−
(1.80) and the logarithm of the density field χ (x, t) = ln ρ(x, t)− (1.82) assumes the
form of the equation
∂
∂t
+ q
∂
∂x
ϕ(x, t; q, p, χ) =
p +
∂
∂p
p
2
+ p
∂
∂χ
ϕ(x, t; q, p, χ) (3.34)
with the initial condition
ϕ(x, 0; q, p, χ) = δ(q
0
(x) − q)δ(p
0
(x) − p)δ
(
χ
0
(x) − χ
)
.
The solution to Eq. (3.34) can be represented in the form
ϕ(x, t; q, p, χ) = exp
−t
q
∂
∂x
− p
∂
∂χ
eϕ(x, t; q, p, χ),

Indicator Function and Liouville Equation 79
where function eϕ(x, t; q, p) satisfies the equation
∂
∂t
− p
2
∂
∂p
eϕ(x, t; q, p, χ) = 3peϕ(x, t; q, p, χ) (3.35)
with the initial condition
ϕ(x, 0; q, p, χ) = δ(q
0
(x) − q)δ(p
0
(x) − p)δ
(
χ
0
(x) − χ
)
.
Solving now Eq. (3.35) by the method of characteristics, we obtain the expression
eϕ(x, t; q, p, χ) =
1
(
1 − pt
)
3
δ(q
0
(x) − q)δ
p
0
(x) −
p
1 − pt
× δ
(
χ
0
(x) − ln
(
1 + tp
0
(x)
)
− χ
)
,
that can be rewritten in the form
eϕ(x, t; q, p, χ) =
[
1 + tp
0
(x)
]
δ(q
0
(x) − q)δ
p
0
(x)
1 + tp
0
(x)
− p
× δ
(
χ
0
(x) − ln
(
1 + tp
0
(x)
)
− χ
)
. (3.36)
Thus, we obtain the solution to Eq. (3.34) in the final form
ϕ(x, t; q, p, χ) = exp
−qt
∂
∂x
[
1 + tp
0
(x)
]
δ(q
0
(x) − q)δ
p
0
(x)
1 + tp
0
(x)
− p
× δ
(
χ
0
(x) − ln
(
1 + tp
0
(x)
)
− χ
)
, (3.37)
in agreement with solutions (1.78), (1.79) and (1.83), pages 36 and 37.
3.2.3 General-Form Nonlinear Equations
Consider now the scalar nonlinear first-order partial differential equation in the general
form (1.84), page 38,
∂
∂t
q(r, t) + H
(
r, t, q, p
)
= 0, q
(
r, 0
)
= q
0
(
r
)
, (3.38)
where p(r, t) = ∂q(r, t)/∂r. In order to derive the closed Liouville equation in this
case, we must supplement Eq. (3.38) with equations for vector p(r, t) and second
derivative matrix U
ik
(r, t) = ∂
2
q(r, t)/∂r
i
∂r
k
.
Introduce now the extended indicator function
ϕ(r, t; q, p, U, I) = δ(q(r, t) − q)δ(p(r, t) − p)δ(U(r, t) − U)δ(I(r, t) − I),
(3.39)

80 Lectures on Dynamics of Stochastic Systems
where we included for generality an additional conserved variable I(r, t) satisfying the
equation of continuity (1.86)
∂
∂t
I(r, t) +
∂
∂r
∂H
(
r, t, q, p
)
∂p
I(r, t)
= 0, I
(
r, 0
)
= I
0
(
r
)
. (3.40)
Equations (3.38), (3.40) describe, for example, wave propagation in inhomo-
geneous media within the frames of the geometrical optics approximation of the
parabolic equation of quasi-optics. Differentiating function (3.39) with respect to time
and using dynamic equations for functions q(r, t), p(r, t), U(r, t) and I(r, t), we gene-
rally obtain an unclosed equation containing third-order derivatives of function q(r, t)
with respect to spatial variable r. However, the combination
∂
∂t
+
∂H
(
r, t, q, p
)
∂p
∂
∂r
ϕ(r, t; q, p, U, I)
will not include the third-order derivatives; as a result, we obtain the closed Liouville
equation in space {q, r, U, I}.
3.3 Higher-Order Partial Differential Equations
If the initial dynamic system includes higher-order derivatives (e.g., Laplace opera-
tor), derivation of a closed equation for the corresponding indicator function becomes
impossible. In this case, only the variational differential equation (the Hopf equation)
can be derived in the closed form for the functional whose average over an ensemble
of realizations coincides with the characteristic functional of the solution to the cor-
responding dynamic equation. Consider such a transition using the partial differential
equations considered in Lecture 1 as examples.
3.3.1 Parabolic Equation of Quasi-Optics
The first example concerns wave propagation in random medium within the frames of
linear parabolic equation (1.89), page 39,
∂
∂x
u(x, R) =
i
2k
1
R
u(x, R) +
ik
2
ε(x, R)u(x, R), u(0, R) = u
0
(R). (3.41)
Equation (3.41) as the initial-value problem possesses the property of dynamic
causality with respect to parameter x. Indeed, rewrite this equation in the integral form
u(x, R) = u
0
(R) +
i
2k
x
Z
0
dξ1
R
u(ξ, R) +
ik
2
x
Z
0
dξε(ξ, R)u(ξ, R). (3.42)
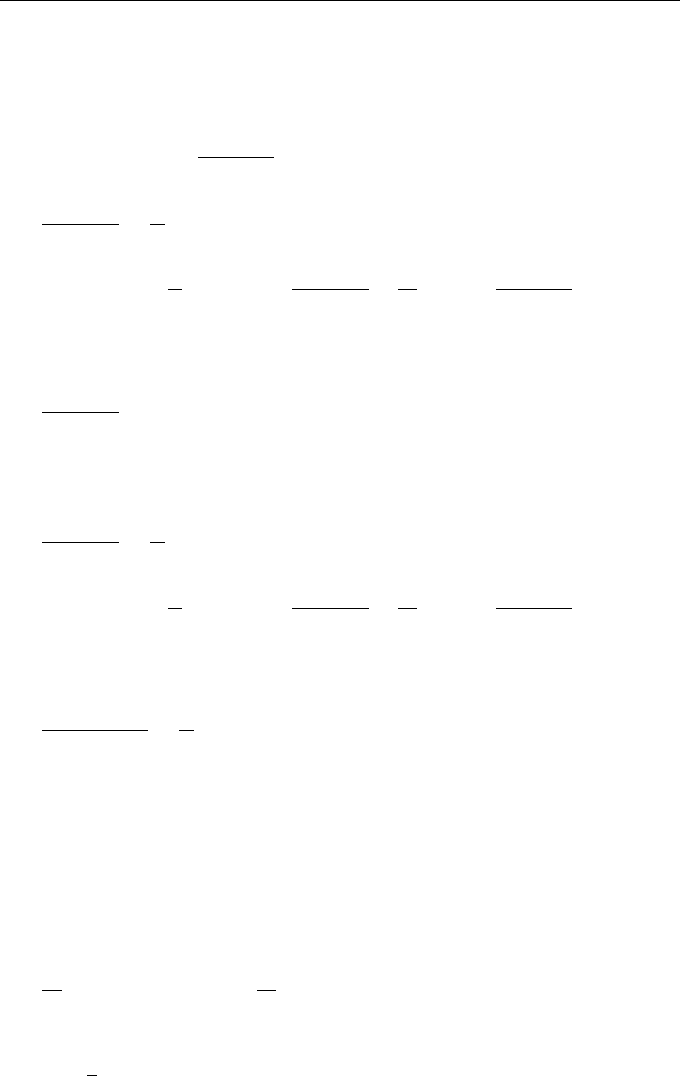
Indicator Function and Liouville Equation 81
Function u(x, R) is a functional of field ε(x, R), i.e.
u(x, R) = u
x, R; ε
ex,
e
R
.
Varying Eq. (3.42) with respect to function ε(x
0
, R
0
), we obtain the integral equation
in variational derivative
δu(x, R)
δε(x
0
, R
0
)
δu(x, R)
δε(x
0
, R
0
)
=
ik
2
θ(x − x
0
)θ(x
0
)δ(R − R
0
)u(x
0
, R)
+
ik
2
x
Z
0
dξε(ξ, R)
δu(ξ, R)
δε(x
0
, R
0
)
+
i
2k
x
Z
0
dξ1
R
δu(ξ, R)
δε(x
0
, R
0
)
. (3.43)
From this equation follows that
δu(x, R)
δε(x
0
, R
0
)
= 0 if x < x
0
or x
0
< 0, (3.44)
which just expresses the dynamic causality property. As a consequence of this fact, we
can rewrite Eq. (3.43) in the form (for 0 < x
0
< x)
δu(x, R)
δε(x
0
, R
0
)
=
ik
2
δ(R − R
0
)u(x
0
, R)
+
ik
2
x
Z
x
0
dξε(ξ, R)
δu(ξ, R)
δε(x
0
, R
0
)
+
i
2k
x
Z
x
0
dξ1
R
δu(ξ, R)
δε(x
0
, R
0
)
, (3.45)
from which follows the equality
δu(x, R)
δε(x − 0, R
0
)
=
ik
2
δ(R − R
0
)u(x, R). (3.46)
Consider now the functional
ϕ[x; v(R
0
), v
∗
(R
0
)] = exp
i
Z
dR
0
u(x, R
0
)v(R
0
) + u
∗
(x, R
0
)v
∗
(R
0
)
, (3.47)
where wavefield u(x, R) satisfies Eq. (3.41) and u
∗
(x, R) is the complex conjugated
function. Differentiating (3.47) with respect to x and using dynamic equation (3.41)
and its complex conjugate, we obtain the equality
∂
∂x
ϕ[x; v(R
0
), v
∗
(R
0
)] = −
1
2k
Z
dR
[
v(R)1
R
u(x, R)
−v
∗
(R)1
R
u
∗
(x, R)
ϕ[x; v(R
0
), v
∗
(R
0
)]
−
k
2
Z
dRε(x, R)
v(R)u(x, R) − v
∗
(R)u
∗
(x, R)
ϕ[x; v(R
0
), v
∗
(R
0
)],

82 Lectures on Dynamics of Stochastic Systems
which can be written as the variational differential equation
∂
∂x
ϕ[x; v(R
0
), v
∗
(R
0
)] =
ik
2
Z
dRε(x, R)
b
M(R)ϕ[x; v(R
0
), v
∗
(R
0
)]
+
i
2k
Z
dR
v(R)1
R
δ
δv(R)
− v
∗
(R)1
R
δ
δv
∗
(R)
× ϕ[x; v(R
0
), v
∗
(R
0
)], (3.48)
with the initial value
ϕ[0; v(R
0
), v
∗
(R
0
)] = exp
i
Z
dR
0
u
0
(R
0
)v(R
0
) + u
∗
0
(R
0
)v
∗
(R
0
)
,
and with the Hermitian operator
b
M(R) = v(R)
δ
δv(R)
− v
∗
(R)
δ
δv
∗
(R)
.
Equation (3.48) is equivalent to the input equation (3.41).
Rewrite problem (3.48) with the initial condition in the integral form
ϕ[x; v(
e
R), v
∗
(
e
R)] = ϕ[0; v(
e
R), v
∗
(
e
R)]
+
ik
2
x
Z
0
dξ
Z
dRε(ξ, R)
b
M(R)ϕ[ξ; v(
e
R), v
∗
(
e
R)]
+
i
2k
x
Z
0
dξ
Z
dR
v(R)1
R
δ
δv(R)
− v
∗
(R)1
R
δ
δv
∗
(R)
× ϕ[ξ; v(
e
R), v
∗
(
e
R)],
and vary the resulting equation with respect to function ε(x
0
, R
0
). Then we obtain that
variational derivative
δϕ[x; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
satisfies the integral equation
δϕ[x; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
= θ(x − x
0
)θ(x
0
)
ik
2
b
M(R
0
)ϕ[x
0
; v(
e
R), v
∗
(
e
R)]
+
ik
2
x
Z
0
dξ
Z
dRε(ξ, R)
b
M(R)
δϕ[ξ; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
+
i
2k
x
Z
0
dξ
Z
dR
v(R)1
R
δ
δv(R)
− v
∗
(R)1
R
δ
δv
∗
(R)
×
δϕ[ξ; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
.
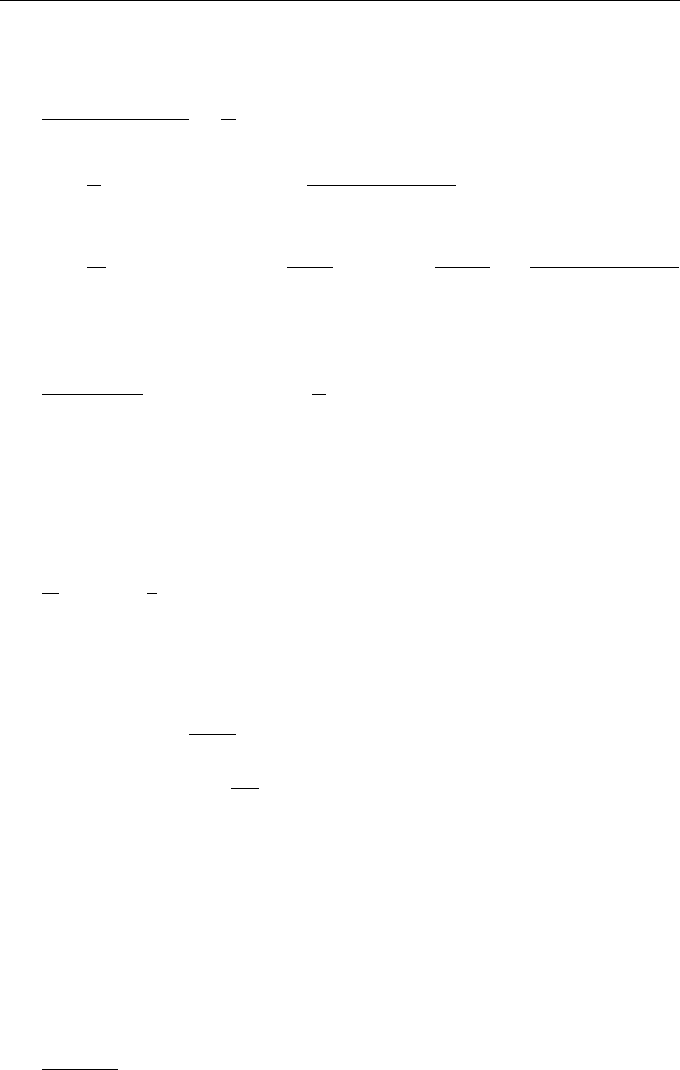
Indicator Function and Liouville Equation 83
In view of the dynamic causality property, we can rewrite it in the form of the equation
(for 0 < x
0
< x)
δϕ[x; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
=
ik
2
b
M(R
0
)ϕ[x
0
; v(
e
R), v
∗
(
e
R)]
+
ik
2
x
Z
x
0
dξ
Z
dRε(ξ, R)
b
M(R)
δϕ[ξ; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
+
i
2k
x
Z
x
0
dξ
Z
dR
v(R)1
R
δ
δv(R)
− v
∗
(R)1
R
δ
δv
∗
(R)
×
δϕ[ξ; v(
e
R), v
∗
(
e
R)]
δε(x
0
, R
0
)
,
from which follows the equality
δ
δε(x − 0, R)
ϕ[x; v(
e
R), v
∗
(
e
R)] =
ik
2
b
M(R)ϕ[x; v(
e
R), v
∗
(
e
R)]. (3.49)
3.3.2 Random Forces in Hydrodynamic Theory of Turbulence
Consider now integro-differential equation (1.102), page 44, for the Fourier harmonics
bu(k, t) of the solution to the Navier–Stokes equation (1.95)
∂
∂t
bu
i
(
k, t
)
+
i
2
Z
dk
1
Z
dk
2
3
αβ
i
(
k
1
, k
2
, k
)
bu
α
(
k
1
, t
)
bu
β
(
k
2
, t
)
− νk
2
bu
i
(
k, t
)
=
b
f
i
(
k, t
)
, (3.50)
where
3
αβ
i
(
k
1
, k
2
, k
)
=
1
(2π)
3
k
α
1
iβ
(
k
)
+ k
β
1
iα
(
k
)
δ(k
1
+ k
2
− k),
1
ij
(
k
)
= δ
ij
−
k
i
k
j
k
2
(i, α, β = 1, 2, 3),
and
b
f (k, t) is the spatial Fourier harmonics of external forces.
Function bu
i
(
k, t
)
satisfies the principle of dynamic causality, which means that the
variational derivative of function
bu
i
(
k, t
)
= bu
i
k, t;
b
f
α
e
k,
e
t
(considered as a functional of field
b
f
(
k, t
)
) with respect to field
b
f
k
0
, t
0
vanishes for
t
0
> t and t
0
< 0,
δbu
i
(
k, t
)
δ
b
f
j
k
0
, t
0
= 0, if t
0
> t or t
0
< 0,
84 Lectures on Dynamics of Stochastic Systems
and, moreover,
δbu
i
(
k, t
)
δ
b
f
j
k
0
, t − 0
= δ
ij
δ(k − k
0
). (3.51)
Consider the functional
ϕ[t; z] = ϕ[t; z(k
0
)] = exp
i
Z
dk
0
bu(k
0
, t)z(k
0
)
. (3.52)
Differentiating this functional with respect to time t and using dynamic equa-
tion (3.50), we obtain the equality
∂
∂t
ϕ[t; z] = −i
Z
dkz
i
(k)
n
νk
2
bu
i
(
k, t
)
−
b
f
i
(
k, t
)
o
ϕ[t; z]
+
1
2
Z
dkz
i
(k)
Z
dk
1
Z
dk
2
3
αβ
i
(
k
1
, k
2
, k
)
bu
α
(
k
1
, t
)
bu
β
(
k
2
, t
)
ϕ[t; z],
which can be rewritten in the functional space as the linear Hopf equation containing
variational derivatives
∂
∂t
ϕ[t; z] = −
1
2
Z
dkz
i
(k)
Z
dk
1
Z
dk
2
3
αβ
i
(
k
1
, k
2
, k
)
δ
2
ϕ[t; z]
δz
α
(
k
1
)
δz
β
(
k
2
)
−
Z
dkz
i
(k)
νk
2
δ
δz
i
(
k
)
− i
b
f
i
(
k, t
)
ϕ[t; z], (3.53)
with the given initial condition at t = 0.
This means that Eq. (3.53) satisfies the condition of dynamic causality; a conse-
quence of this condition is the equality
δ
δ
b
f (k, t − 0)
ϕ[t; z] = iz(k)ϕ[t; z]. (3.54)
In a similar way, considering the space-time harmonics of the velocity field bu
i
(K),
where K is the four-dimensional wave vector {k, ω} and bu
∗
i
(K) = bu
i
(−K) because
field u
i
(r, t) is real, we obtain the nonlinear integral equation (1.103), page 45,
(iω + νk
2
)bu
i
(
K
)
+
i
2
Z
d
4
K
1
Z
d
4
K
2
3
αβ
i
(
K
1
, K
2
, K
)
bu
α
(
K
1
)
bu
β
(
K
)
=
b
f
i
(
K
)
,
(3.55)
where
3
αβ
i
(
K
1
, K
2
, K
)
=
1
2π
3
αβ
i
(
k
1
, k
2
, k
)
δ(ω
1
+ ω
2
− ω),
and
b
f
i
(K) are the space-time Fourier harmonics of external forces. In this case, dealing
with the functional
ϕ[z] = ϕ[z(K
0
)] = exp
i
Z
d
4
K
0
bu(K
0
)z(K
0
)
, (3.56)

Indicator Function and Liouville Equation 85
we derive the linear variational integro-differential equation of the form
(iω + νk
2
)
δϕ[z]
δz
i
(
K
)
= i
b
f
i
(
K
)
ϕ[z]
−
1
2
Z
d
4
K
1
Z
d
4
K
2
3
αβ
i
(
K
1
, K
2
, K
)
δϕ[z]
δz
α
(
K
1
)
δz
β
(
K
2
)
.
(3.57)
Problems
Problem 3.1
Derive the Liouville equation for the Hamiltonian system of equations (1.14),
page 9.
Solution Indicator function ϕ(r, v, t) = δ(r(t) − r)δ(v(t) − v) satisfies the Liou-
ville equation (equation of continuity in the {r, v} space)
∂ϕ(r, v, t)
∂t
=
−
∂
∂r
k
∂H(r, v, t)
∂v
k
+
∂
∂v
k
∂H(r, v, t)
∂r
k
ϕ(r, v, t)
that can be rewritten in the form
∂ϕ(r, v, t)
∂t
=
{
H(r, v, t), ϕ(r, v, t)
}
, (3.58)
where
{
H, ϕ
}
=
∂H
∂r
k
∂ϕ
∂v
k
−
∂H
∂v
k
∂ϕ
∂r
k
is the Poisson bracket of functions H(r, v, t) and ϕ(r, v, t).
Problem 3.2
Determine the relationship between the Eulerian and Lagrangian indicator func-
tions for linear problem (3.14), page 73.
Solution
ϕ(r, t; ρ) =
Z
dr
0
∞
Z
0
dj jϕ
Lag
(r, ρ, j, t|r
0
).
Problem 3.3
Derive Eq. (3.18), page 74, from the dynamic system (1.42), (1.43), page 24, in
the Lagrangian description.
