Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


106 Lectures on Dynamics of Stochastic Systems
Expression (1.53), page 29, allows obtaining the following representations for the
vortex field correlation and spectral tensors [28]:
ω
i
(r, t)ω
j
(r
0
, t
0
)
= −δ
ij
1
r
B
ll
(r − r
0
, t − t
0
) +
∂
2
B
ll
(r − r
0
, t − t
0
)
∂r
i
∂r
j
+ 1
r
B
ij
(r − r
0
, t − t
0
),
ij
(k, t − t
0
) = (δ
ij
k
2
− k
i
k
j
)E
ll
(k, t − t
0
) − k
2
E
ij
(k, t − t
0
).
Convolving them with respect to indices i and j and setting r = r
0
, we obtain the
expressions for the correlation and spectral functions of the vortex field
ω
i
(r, t)ω
i
(r, t
0
)
= −1
r
B
ll
(0, t − t
0
) = −
u(r, t)1
r
u(r, t
0
)
,
ii
(k, t − t
0
) = k
2
E
ii
(k, t − t
0
).
(4.51)
Note that the procedure similar to that used to calculate vortex field variance and
spectrum allows additionally calculating average helicity of the velocity field
χ(r, t) = u(r, t)ω(r, t) = u(r, t) · curl u(r, t),
in the three-dimensional case in the absence of reflection symmetry. Indeed, the use
of Eq. (1.54), page 29, results in the following expression for statistically averaged
quantity
ω
i
(r, t)u
j
(r, t)
ω
i
(r, t)u
p
(r
0
, t)
r=r
0
= ε
ijk
∂u
k
(r, t)
∂r
j
u
p
(r
0
, t)
r=r
0
= ε
ijk
∂
∂r
j
B
kp
(r, 0)
r=0
= lim
r→0
ε
ijk
∂
∂r
j
C(r, 0)ε
kpm
r
m
= C(0, 0)ε
ijm
ε
mpj
= 2C(0, 0)δ
ip
,
and, hence, the average helicity of the Gaussian random field in the three-dimensional
case is
h
χ(r, t)
i
= 6C(0, 0). (4.52)
The isotropic portion of correlation tensor corresponds to the spatial spectral tensor
of the form
E
ij
(k, τ ) = E
s
ij
(k, τ ) + E
p
ij
(k, τ ),
where the spectral components of the tensor of velocity field have the following
structure
E
s
ij
(k, τ ) = E
s
(k, τ )
δ
ij
−
k
i
k
j
k
2
, E
p
ij
(k, τ ) = E
p
(k, τ )
k
i
k
j
k
2
.

Random Quantities, Processes, and Fields 107
Here, E
s
(k, τ ) and E
p
(k, τ ) are the solenoidal and potential components of the spectral
density of velocity field, respectively.
Define now function B
ij
(r) as the integral of correlation function (4.49) over time,
i.e.,
B
ij
(r) =
∞
Z
0
dτ B
ij
(r, τ ) = B
iso
ij
(r) + C(r)ε
ijk
r
k
. (4.53)
Then, B
ij
(0) = D
0
δ
ij
and, hence, quantity
B
ii
(0) = D
0
d = τ
0
σ
2
u
=
Z
dk
(
d − 1
)
E
s
(k) + E
p
(k)
, (4.54)
defines temporal correlation radius of the velocity field τ
0
. Here, σ
2
u
= B
ii
(0, 0) =
u
2
(r, t)
is the variance of the velocity field, and functions E
s
(k) and E
p
(k) are defined
as follows
E
s
(k) =
∞
Z
0
dτ E
s
(k, τ ), E
p
(k) =
∞
Z
0
dτ E
p
(k, τ ). (4.55)
The use of correlation function (4.53) appreciably simplifies calculations dealing
with spatial derivatives of the velocity field. Indeed, we have
∂B
ij
(0)
∂r
k
= C(0)ε
ijk
, (4.56)
−
∂
2
B
ij
(0)
∂r
k
∂r
l
=
D
s
d(d + 2)
(d + 1)δ
kl
δ
ij
− δ
ki
δ
lj
− δ
kj
δ
li
+
D
p
d(d + 2)
δ
kl
δ
ij
+ δ
ki
δ
lj
+ δ
kj
δ
li
, (4.57)
∂
3
B
kp
(0)
∂r
n
∂r
m
∂r
j
= −2α
ε
kpj
δ
nm
+ ε
kpm
δ
nj
+ ε
kpn
δ
mj
, (4.58)
and, consequently,
∂
3
B
kp
(0)
∂r
2
∂r
j
= −2α(d + 2)ε
kpj
,

108 Lectures on Dynamics of Stochastic Systems
where
D
s
=
Z
dk k
2
E
s
(k) =
1
d − 1
∞
Z
0
dτ hω(r, t +τ )ω(r, t)i,
D
p
=
Z
dk k
2
E
p
(k) =
∞
Z
0
dτ
∂u(r, t + τ )
∂r
∂u(r, t)
∂r
,
C(r) = C(0) − αr
2
,
(4.59)
and ω(r, t) is the velocity field vortex.
4.2.5 Logarithmically Normal Random Process
Note that the so-called logarithmically normal (lognormal) random process y(t)
y(t) = e
z(t)
,
whose logarithm is the Gaussian random process, is described by the one-time proba-
bility density P(y, t) of the form
P(y, t) =
1
y
P(z = ln y, t) =
1
y
p
2πσ
2
(t)
exp
(
−
ln
2
e
−
h
z(t)
i
y
2σ
2
(t)
)
,
and, consequently, the corresponding integral distribution function assumes the form
F(y, t) =
y
Z
−∞
dy
0
P(y
0
, t) =
1
p
2πσ
2
(t)
y
Z
−∞
dy
0
y
0
exp
(
−
ln
2
e
−
h
z(t)
i
y
0
2σ
2
(t)
)
=
1
p
2πσ
2
(t)
ln
e
−
h
z(t)
i
y
Z
−∞
dz exp
−
z
2
2σ
2
(t)
= Pr
ln
e
−
h
z(t)
i
y
σ (t)
!
,
where probability integral Pr(z) is defined by Eq. (4.20), page 94.
In view of Eq. (4.21), page 94, the right-hand side of this equality turns into 1/2 if
e
−
h
z(t)
i
y(t) = 1,
which means that the typical realization curve y
∗
(t) of the lognormal random process
y(t) is given by the equality
y
∗
(t) = e
h
z(t)
i
= e
h
ln y(t)
i
. (4.60)
Random Quantities, Processes, and Fields 109
Note that, if we know the moment functions of random process y(t) as functions
of time, i.e., if we know functions
h
y
n
(t)
i
(n = 1, 2, . . .), we know also the statistical
characteristics of random process z(t) = ln y(t). Indeed,
y
n
(t)
=
D
e
n ln y(t)
E
= exp
n
h
ln y(t)
i
+
n
2
2
σ
2
ln y
(t)
,
and, consequently,
h
ln y(t)
i
= lim
n→0
1
n
ln
y
n
(t)
, σ
2
ln y
(t) = lim
n→∞
2
n
2
ln
y
n
(t)
. (4.61)
Further, analyzing statistical topography of random processes and fields, we will
use, in line with the integral distribution function, functions
V(y, t) =
∞
Z
y
dy
0
P(y
0
, t) and Y(y, t) =
∞
Z
y
y
0
dy
0
P(y
0
, t),
closely related to the probability integral Pr(z).
For function V(y, t), we have
V(y, t) =
1
p
2πσ
2
(t)
∞
Z
y
dy
0
y
0
exp
(
−
ln y
0
−
h
z(t)
i
2
2σ
2
(t)
)
=
1
√
2π
∞
Z
ln y−
h
z(t)
i
σ (t)
dz exp
−
z
2
2
= Pr
−
ln y −
h
z(t)
i
σ (t)
= Pr
1
σ (t)
ln
1
y
e
h
z(t)
i
. (4.62)
For function Y(y, t), we obtain the expression
Y(y, t) =
1
p
2πσ
2
(t)
∞
Z
y
dy
0
exp
(
−
ln y
0
−
h
z(t)
i
2
2σ
2
(t)
)
=
1
√
2π
e
h
z(t)
i
+σ
2
(t)/2
∞
Z
ln y−
h
z(t)
i
−σ
2
(t)
σ (t)
dz exp
−
z
2
2
= e
h
z(t)
i
+σ
2
(t)/2
Pr
−
ln y −
h
z(t)
i
− σ
2
(t)
σ (t)
= e
h
z(t)
i
+σ
2
(t)/2
Pr
1
σ (t)
ln
1
y
e
h
z(t)
i
+σ
2
(t)
. (4.63)

110 Lectures on Dynamics of Stochastic Systems
Note that for random processey(t) = y
0
y(t), i.e.,
ey(t) = y
0
e
z(t)
,
instead of Eqs. (4.62), (4.63) we have the expressions
e
V(y, t) = Pr
1
σ (t)
ln
y
0
y
e
h
z(t)
i
,
e
Y(y, t) = y
0
e
h
z(t)
i
+σ
2
(t)/2
Pr
1
σ (t)
ln
y
0
y
e
h
z(t)
i
+σ
2
(t)
.
(4.64)
4.2.6 Discontinuous Random Processes
Consider now some examples of discontinuous processes. The discontinuous pro-
cesses are the random functions that change their time-dependent behavior at dis-
crete instants t
1
, t
2
, . . . given statistically. The description of discontinuous processes
requires first of all either the knowledge of the statistics of these instants, or the knowl-
edge of the statistics of number n(0, t) of instants t
i
falling in time interval (0, t). In
the latter case, we have the equality
n(0, t) = n(0, t
0
) + n(t
0
, t), 0 ≤ t
0
≤ t.
The quantity n(0, t) by itself is a random process, and Fig. 4.2 shows its possible
realization.
The set of points of discontinuity t
1
, t
2
, . . . of process z(t) is called the stream
of points. In what follows, we will consider Poisson’s stationary stream of points in
which the probability of falling n points in interval (t
1
, t
2
) is specified by Poisson’s
formula
P
n(t
1
,t
2
)=n
=
h
n(t
1
, t
2
)
i
n
n!
e
−n(t
1
,t
2
)
, (4.65)
with the mean number of points in interval (t
1
, t
2
) given by the formula
n(t
1
, t
2
) = ν|t
1
− t
2
|,
t
1
t
2
t
3
t
4
t
0
n(0, t)
1
2
3
4
Figure 4.2 A possible realization of process n(0, t).

Random Quantities, Processes, and Fields 111
where ν is the mean number of points per unit time. It is assumed here that the num-
bers of points falling in nonoverlapping intervals are statistically independent and the
instants at which points were fallen in interval (t
1
, t
2
) under the condition that their
total number was n are also statistically independent and uniformly distributed over
the interval (t
1
, t
2
). The length of the interval between adjacent points of discontinuity
satisfies the exponential distribution.
Poisson stream of points is an example of the Markovian processes.
Consider now random processes whose points of discontinuity form Poisson’s
streams of points. Currently, three types of such process – Poisson’s process, teleg-
rapher’s process, and generalized telegrapher’s process – are mainly used to model
problems in physics. Below, we focus our attention on these processes.
Poisson’s (Impulse) Random Process
Poisson’s (impulse) random process z(t) is the process described by the formula
z(t) =
n
X
i=1
ξ
i
g(t − t
i
), (4.66)
where random quantities ξ
i
are statistically independent and distributed with probabi-
lity density p(ξ); random points t
k
are uniformly distributed on interval (0, T), so that
their number n obeys Poisson’s law with parameter ¯n = νT; and function g(t) is the
deterministic function that describes the pulse envelope (g(t) = 0 for t < 0).
The characteristic functional of Poisson’s random process z(t) assumes the form
8[t;v(τ )] = exp
ν
t
Z
0
dt
0
W
t
Z
t
0
dτ v(τ )g(t − t
0
)
− 1
, (4.67)
where
W(v) =
∞
Z
−∞
dξp(ξ )e
iξv
,
is the characteristic function of random quantity ξ . Consequently, functional 2[t;v(τ )]
is given by the formula
2[t;v(τ )] = ln 8[t;v(τ )]
= ν
t
Z
0
dt
0
∞
Z
−∞
dξp(ξ )
exp
iξ
t
Z
t
0
dτ v(τ )g(t − t
0
)
− 1
, (4.68)

112 Lectures on Dynamics of Stochastic Systems
and cumulant functions assume the form
K
n
(t
1
, . . . , t
n
) = ν
ξ
n
min{t
1
,...,t
n
}
Z
0
dt
0
g(t − t
0
) . . . g(t
n
− t
0
). (4.69)
We consider two types of Poisson’s processes important for applications.
1. Let g(t) = θ (t) =
1, t > 0,
0, t < 0,
, i.e., z(t) =
n
P
i=1
ξ
i
θ(t − t
i
). In this case,
K
n
(t
1
, . . . , t
n
) = ν
ξ
n
min{t
1
, . . . , t
n
}.
If additionally ξ = 1, then process z(t) ≡ n(0, t), and we have
K
n
(t
1
, . . . , t
n
) = ν min{t
1
, . . . , t
n
},
2[t;v(τ )] = ν
t
Z
0
dt
0
exp
i
t
Z
t
0
dτ v(τ )
− 1
.
(4.70)
2. Let now g(t) = δ(t). In this case, process
z(t) =
n
X
i=1
ξ
i
δ(t − t
i
)
is usually called the shot noise process. This process is a special case of the delta-correlated
processes (see Sect. 5.5, page 130). For such a process, functional 2[t;v(τ )] is
2[t;v(τ )] = ν
t
Z
0
dτ
∞
Z
−∞
dξ p(ξ )
n
e
iξv(τ )
− 1
o
(4.71)
and cumulant functions assume the form
K
n
(t
1
, . . . , t
n
) = ν
ξ
n
δ(t
1
− t
2
)δ(t
2
− t
3
) . . . δ(t
n−1
− t
n
).
Note that Poisson’s process z(t) with arbitrary given impulse function g(t) can be always
expressed in terms of Poisson’s delta-correlated random process z
δ
(t) by the formula
z(t) =
t
Z
0
dτ g(t − τ )z
δ
(τ ). (4.72)
Telegrapher’s Random Process
Consider now statistical characteristics of telegrapher’s random process (Fig. 4.3)
defined by the formula
z(t) = a(−1)
n(0,t)
(z(0) = a, z
2
(t) ≡ a
2
), (4.73)
where n(t
1
, t
2
) is the random sequence of integers equal to the number of points of
discontinuity in interval (t
1
, t
2
).
We consider two cases.

Random Quantities, Processes, and Fields 113
t
z (t )
a
−a
Figure 4.3 A possible realization of telegrapher’s random process.
1. We will assume first that amplitude a is the deterministic quantity.
For the two first moment functions of process z(t), we have the expressions
h
z(t)
i
= a
∞
X
n(0,t)=0
(−1)
n(0,t)
P
n(0,t)
= ae
−2n(0,t)
= ae
−2νt
,
h
z(t
1
)z(t
2
)
i
= a
2
D
(−1)
n(0,t
1
)+n(0,t
2
)
E
= a
2
D
(−1)
n(t
2
,t
1
)
E
= a
2
e
−2n(t
2
,t
1
)
= a
2
e
−2ν(t
1
−t
2
)
(t
1
≥ t
2
). (4.74)
The higher moment functions for t
1
> t
2
> . . . > t
n
satisfy the recurrence relationship
M
n
(t
1
, . . . , t
n
) =
h
z(t
1
) . . . z(t
n
)
i
= a
2
D
(−1)
n(0,t
1
)+n(0,t
2
)+n(0,t
3
)+···+n(0,t
n
)
E
= a
2
D
(−1)
n(t
2
,t
1
)
ED
(−1)
n(0,t
3
)+···+n(0,t
n
)
E
=
h
z(t
1
)z(t
2
)
i
M
n−2
(t
3
, . . . , t
n
). (4.75)
This relationship is very similar to Eq. (4.42) for the Gaussian process with correlation
function B(t
1
, t
2
). The only difference is that the right-hand side of Eq. (4.75) coincides
with only one term of the sum in Eq. (4.42), namely, with the term that corresponds to the
above order of times.
Consider now the characteristic functional of this process
8
a
[t;v(τ )] =
*
exp
i
t
Z
0
dτ z(τ )v(τ )
+
,
where index a means that amplitude a is the deterministic quantity. Expanding the charac-
teristic functional in the functional Taylor series and using recurrence formula (4.75), we
obtain the integral equation
8
a
[t;v(τ )] = 1 +ia
t
Z
0
dt
1
e
−2νt
1
v(t
1
)
− a
2
t
Z
0
dt
1
t
1
Z
0
dt
2
e
−2ν(t
1
−t
2
)
v(t
1
)v(t
2
)8
a
[t
2
;v(τ )]. (4.76)

114 Lectures on Dynamics of Stochastic Systems
Differentiating Eq. (4.76) with respect to t, we obtain the integro-differential equation
d
dt
8
a
[t;v(τ )] = iae
−2νt
v(t) − a
2
v(t)
t
Z
0
dt
1
e
−2ν(t−t
1
)
v(t
1
)8
a
[t
1
;v(τ )]. (4.77)
2. Assume now amplitude a is the random quantity with probability density p(a). To obtain
the characteristic functional of process z(t) in this case, we should average Eq. (4.77) with
respect to random amplitude a. In the general case, such averaging cannot be performed
analytically. Analytical averaging of Eq. (4.77) appears to be possible only if probability
density of random amplitude a has the form
p(a) =
1
2
[
δ
(
a −a
0
)
+ δ
(
a +a
0
)
]
, (4.78)
with
h
a
i
= 0 and
a
2
= a
2
0
(in fact, this very case is what is called usually telegrapher’s
process). As a result, we obtain the integro-differential equation
d
dt
8[t;v(τ )] = −a
2
0
v(t)
t
Z
0
dt
1
e
−2ν(t−t
1
)
v(t
1
)8[t
1
;v(τ )]. (4.79)
Now, we dwell on an important limiting theorem concerning telegrapher’s random pro-
cesses.
Consider the random process
ξ
N
(t) = z
1
(t) + ··· + z
N
(t),
where all z
k
(t) are statistically independent telegrapher’s processes with zero-valued means
and correlation functions
h
z(t)z(t + τ )
i
=
σ
2
N
e
−α|τ |
.
In the limit N → ∞, we obtain that process ξ(t) = lim
N→∞
ξ
N
(t) is the Gaussian random
process with the exponential correlation function
h
ξ(t)ξ(t + τ )
i
= σ
2
e
−α|τ |
,
i.e., the Gaussian Markovian process. Thus, process ξ
N
(t) for finite N is the finite-number-
of-states process approximating the Gaussian Markovian process.
Generalized Telegrapher’s Random Process
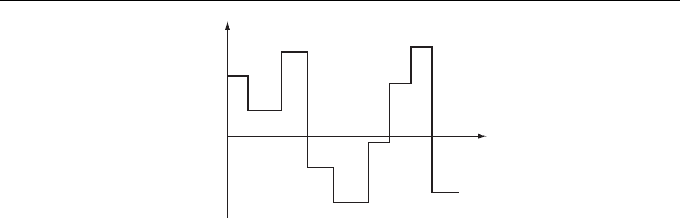
Consider now generalized telegrapher’s process defined by the formula
z(t) = a
n(0,t)
. (4.80)
Here, n(0, t) is the sequence of integers described above and quantities a
k
are assumed
statistically independent with distribution function p(a). Figure 4.4 shows a possible
realization of such a process.
Random Quantities, Processes, and Fields 115
a
0
a
2
a
1
a
3
a
4
a
5
a
6
a
7
a
8
t
z (t )
Figure 4.4 A possible realization of generalized telegrapher’s random process.
For process z(t), we have
h
z(t)
i
=
∞
X
k=0
a
k
δ
k,n(0,t)
=
h
a
i
,
h
z(t
1
)z(t
2
)
i
=
∞
X
k=0
∞
X
k=0
h
a
k
a
l
i
δ
k,n(0,t
1
)
δ
l,n(0,t
2
)
=
D
a
2
E
(
∞
X
k=0
δ
k,n(0,t
1
)
δ
0,n(t
2
,t
1
)
+ 1 −
∞
X
k=0
δ
k,n(0,t
2
)
δ
0,n(t
2
,t
1
)
)
=
D
a
2
E
e
−ν(t
1
−t
2
)
+
D
a
2
E
1 − e
−ν(t
1
−t
2
)
(t
1
> t
2
),
and so on. In addition, the probability of absence of points of discontinuity in interval
(t
2
, t
1
) is given by the formula
P
n(t
2
,t
1
)=0
=
δ
0,n(t
2
,t
1
)
= e
−ν|t
1
−t
2
|
.
Earlier, we mentioned that Poisson’s stream of points and processes based on these
streams are the Markovian processes. Below, we consider this important class of ran-
dom processes in detail.
4.3 Markovian Processes
4.3.1 General Properties
In the foregoing section, we considered the characteristic functional that describes all
statistical characteristics of random process z(t). Specification of the argument of the
functional in the form
v(t) =
n
X
k=1
v
k
δ(t − t
k
)
