Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

561
Відповіді до задач та прикладів
21)
2
40
2314
x
x
; 22) (x
2
+ 1)
sin x
(
2
2sin
1
xx
x
– cos x
ln(x
2
+ 1));
23) (ln x)
x
(
1
ln
x
+ lnln x); 24) –4(1 – 4x
3
)
cos 4x
(
2
3
3cos4
14
xx
x
+
sin 4x
ln(1 – 4x
3
)); 25)
1
1
(1 ctg 3 )
x
x
x
3
sin3
(
sin3 cos3
)
xx x
§
¨
©
–
–
ln(1 ctg3 )
x
x
·
¸
¹
; 26)
33
3
632
3
ctg arctg
(1 ) (arctg )
xx
xx
ee
ee
; 27)
2
1
2arct
g
1
x
x
;
28)
arcsin2
2
2
14
x
e
x
; 29)
ln
2
(ln 1)ln2
2
ln
x
x
x
x
; 30)
3
3
23 9xx
;
31) 3x
2
arctg x
3
+
5
6
3
1
x
x
; 32)
1
x
–
2
1
x
x
+ctg x; 33)
23
6
(
32 73
)(
3
)
2( 1) 2
x
xx
xx
;
34) 2x
ln x–1
ln x; 35)
2
ln( )
2
(2 )
2( ) ln( )
ax bx c
ax b e
ax bx c ax bx c
;
36)
22 2
arctg 1 (2 ) 1
x
xx x
; 37)
2
()(
1ln
()
a
ax b ax b
;
38)
2
414
(
14
)
14
x
xx
§
¨
¨
©
+ arcsin 4x
·
¸
¹
; 39) 10
x
tg
x
ln10(tgx +
2
cos
x
x
);
40)
2
42
3
2( 2)( 11 1)
3( 5) ( 1)
xxx
xx
; 41)
(
2
)
x
x
x
x
§
¨
¨
©
+
ln2
2
x
x
·
¸
¹
;
42)
2
1
1
(2 2 )arctg
1
xx
x
; 43) 2sin x(xsinxcosx
2
+ cosxsinx
2
);
562
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
44)
2
3
2
23(1 3)
x
xxx
; 45)
2
ct
g
(
t
g
2
)
x
x
2
4ctg
lntg2
2
sin4
2sin
2
x
x
x
x
§·
¨¸
¨¸
¨¸
¨¸
©¹
.
4.10. 1)
(
ln
)
(
ln
)
y
xx
yy
x
y
xx
y
; 2)
sin sin
cos cos
y
x
y
xx
y
; 3)
(1 )
(1)
y
x
xy
;
4)
1
3
xy
xy
y
e
x
e
=
1( 3)
(3)3
y
xy
xx y
; 5)
sin( ) cos
sin sin( ) sin
x
yy x
x
xy y
;
6)
(1 )
(2 1)
y
x
xy
; 7)
2
2
x
y
xy
x
ye
x
ey
=
22
22
2( )
()2
x
yx y
x
xy y
. 4.11. 1)
2
31
2
t
t
;
2) ctg
2
t
; 3) –1; 4)
2
t
; 5)
cos sin
1sin cos
M
MM
M
MM
; 6)
2
2
1
(2 3 )
t
ttt
;
7)
1tg
1tg
t
t
. 4.12. a)
2
23
6
(
21
)
(
1
)
xx
x
; б)
2
2
1
x
x
+ 2arctg x; в)
23
(
1
)
x
x
;
г)
2
223
()
a
ax
; д)
2
23
arcsin 1
(1 )
x
xx
x
. 4.16. a) 2x – y + 5 = 0,
x + 2y – 5 = 0; б) 4x – 3y + 1 = 0, 3x + 4y – 18 = 0, 4x + 3y + 1 = 0,
3
x – 4y – 18 = 0; в) x + y – 4 = 0, x – y – 2 = 0. 4.17. (3;4), (–3;–4).
4.20. 1) 5
ln tg
x
2ln3
sin2
x
dx; 2)
2
2
12arctg
1
2arcsin 1
x
x
xx
§·
¨¸
©¹
dx;
3)
2
1
2
2
22
3ln39
x
x
x
x
§·
¨¸
¨¸
©¹
dx; 4) dy=
55
10
5
(
21
)
1
xx
x
ee
e
dx; якщо х = 0
і
dx = 0,1, то dy = 0,25. 4.21. a) 0,0100; б) 1,9895. 4.27. 1) 1; 2)
1
2
;

563
Відповіді до задач та прикладів
3) 2; 4) 1; 5) 1; 6) 0; 7) 0; 8) 1; 9) 1; 10) e
2
. 4.39. 1) E
x
(y)=
2
2(1 )
12
xx
xx
,
E
1
(y) = 0; 2) E
x
(y) = 5x, E
1
(y) = 5, E
0
(y) = 0, E
2
(y) = 10; 3) E
x
(y)=
1
ln
x
,
E
10
(y)=
1
ln10
|
0,4343; E
e
(y) = 1,
4
()
e
Ey
= 0,25; 4) E
x
(y) = 1 – 2x
2
,
E
1
(y) = –1, E
2
(y) = –7. 4.40. 1) E
10
(K)
|
0,91; E
50
(K)
|
–0,33;
2) E
1
(K)
|
0,87; E
2
(K)
|
1,25. 4.41. 1,5. 4.42. 146 од. 4.43. 9 грош. од.,
7 грош.
од. 4.44. E
p
(q)=
2
(3 4 )
238
pp
pp
, E
1
(q)=
1
9
. 4.45. a) 3 грош. од.;
б) E
p
(q) = –0,75, E
p
(s) = 1; в) 1,25%. 4.46. 1. a) x = 20; b) E
2
(K)
|
0,039;
E
50
(K)
|
1,788; 2. a) x = 50; b) E
5
(K) = 0,0198; E
25
(K) = 0,4. 4.47. 3. 4.53.
1) функція зростає на інтервалі
(
;
)
f f
; 2) функція зростає на інтер+
валах
(
f
;–2)
(1;
f
), спадає на інтервалі (–2;1); 3) функція зрос+
тає на інтервалі
(–1; 1), спадає на інтервалах (
f
;–1)
(1;
f
);
4) спадає на інтервалі (
f
;0), зростає на інтервалі (–0;
f
); 5) спадає
на інтервалах (
f
;0)
(0;1), зростає на інтервалі (1;
f
). 4.54. 1) точка
х
1
= 0 — точка максимуму, f(0) = 1, точка х
2
= 1 — точка мінімуму,
f(1) = 0; 2) точка х
1
= 1 — точка максимуму, f(1) = 1, точка х
2
= 3 —
точка мінімуму,
f(3) = –3; 3) точка х
1
= 0 — точка мінімуму, f(0) = 0,
точка
х
2
= 1 — точка максимуму, f(1) =
79
, точка х
3
= 4 — точка
мінімуму,
f(4) =
128
3
; 4) точка х
1
= –1 — точка максимуму, f(–1) = 0,
точка
х
2
=
1
5
— точка мінімуму, f(–1/5)=
331
1
3125
, точка х
3
= 1 —
не є точкою екстремуму; 5) точка
х = 0 — точка мінімуму, f(0) = 0;
6) точка х =
2r
— точка мінімуму, f(
2r
) = 4; 7) точка х
1
= 0 — точка
мінімуму,
f(0) = 0, точка х
2
= 2 — точка максимуму, f(2) =
2
4
e
;
8)
точка х = e — точка мінімуму, f(e) = e; 9) точка х=–1 — точка
564
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
мінімуму, f(–1) = ln
2
–
4
S
; 10) екстремумів немає; 11) точка х=
1
e
—
точка мінімуму,
f(
1
e
) =
1
2e
; 12) точка х
1
= –3 — точка, максиму+
му,
f(–3)=3
3
3
, точка х
2
= 2 — точка мінімуму, f(2)=
3
44
; 13) точка
х
1
= 1 –
19
— точка мінімуму, f(1–
19
)
|
–14, точка х
2
= 1+
19
—
точка максимуму,
f(1+
19
)
|
5,5; 14) точка х
1
= 0 — точка максиму+
му,
f(0) = 0, точка х
2
= 1 — точка мінімуму, f(1)=
2
3
; 15) точка х
1
=1 —
точка максимуму,
f(1) = 2,5, точка х
2
= e — точка мінімуму,
f(e)=
(4 )
2
ee
|
1,76. 4.55. х
1
= –4 — точка мінімуму, f(–4) =
365
3
,
х
2
= 2 — точка максимуму, f(2)=
67
3
, х
3
= 3 — точка мінімуму, f(3) =
85
4
,
на відрізку [–5;2]
у
найбільше
= у(2) =
67
3
, у
найменше
= у(–4) = –
365
3
. 4.56.
a)
[2;1]
min
f(x)=f(
1r
)=2,
[2;1]
max
f(x)=f(–2)=11; б)
[1;3]
min
f(x)=f(3)=
5
13
,
[1;3]
max
f(x)=f(0)=1; в)
[4;4]
min
f(x)=f(–4)=–41,
[4;4]
max
f(x)=f(–1)=40;
г)
[0;3]
min
f(x)=f(0)=–10,
[0;3]
max
f(x)=f(2)=10; д)
[1; ]
min
e
f(x)=f(2)=2(1–ln2),
[1; ]
max
e
f(x)=f(1)=1; e)
[1; ]
min
e
f(x)=f(1)=0,
[1; ]
max
e
f(x)=f(e)=e
2
; є)
[2;1]
min
f(x)=
=f
(0)=1,
[2;1]
max
f(x)=f(–2)=3. 4.60. x=
2
3
a, V=
2
27
a
3
. 4.61. 3,6 i 4 cм.
4.62. Радіус основи дорівнює висоті R=
3
V
S
. 4.63. Довжина сторінки
565
Відповіді до задач та прикладів
30 см, а ширина — 20 см. 4.64.
a
h
=2. 4.65. AP=l–a
ctg
D
, де cos
D
=
1
m
.
4.70. 1) точка перегину (1;–2), при
f
< x < 1 крива опукла, а при
1
< x <
f
крива вгнута; 2) точки перегину (–3;294) і (2;114), при
f
< x < –3 та 2 < x <
f
крива опукла, а при –3 < x < 2 крива
вгнута;
3) крива вгнута на всій області визначення:
f
< x < 2 і
2
< x <
f
; 4) точка перегину (0;2), при х < 0 крива вгнута, а при
x > 0 крива опукла. 4.72. 1) горизонтальна асимптота у=0, верти+
кальні асимптоти
х=–2 та х=2; 2) горизонтальна асимптота у=1, вер+
тикальна асимптота
х=–4; 3) горизонтальна асимптота у=0, верти+
кальна асимптота
х=0; 4) вертикальна асимптота х=
2
3
, похила
асимптота
у=
1
2
х–
3
4
; 5) вертикальна асимптота х=–6, похила асимп+
тота
у=2х–11; 6) горизонтальна асимптота у=0 при
x of
;
7)
вертикальна асимптота х=0, похила асимптота у=х. 4.74. 1) виз+
начена:
х
(;)f f
; графік симетричний відносно початку коорди+
нат;
у
max
=
1
2
при х = 1, у
min
=
1
2
при х=–1; точки перегину графіка
(
3
;
3
4
); асимптота у=0; 2) визначена: х
(
f
;–1)
(–1;1)
(1;
f
);
графік симетричний відносно осі ординат;
у
min
=1 при х=0; максимумів
немає; точок перегину немає; асимптоти
х=
1r
, у=0; 3) визначена:
х
(
f
;–1)
(–1;1)
(1;
f
); графік симетричний відносно почат+
ку координат; екстремумів немає; точка перегину
(0;0); асимптоти
х=
1r
, у=0; 4) не визначена при х=
1r
; графік симетричний відносно
осі ординат;
у
max
=0 при х=0, мінімумів немає; при х < –1 зростає; при
х > 1 спадає; точок перегину немає; асимптоти х=
1r
, у=1; 5) визна+
чена:
х
(
f
,0)
(0;
f
); у
min
=3 при х=
1
2
; максимумів немає; точка
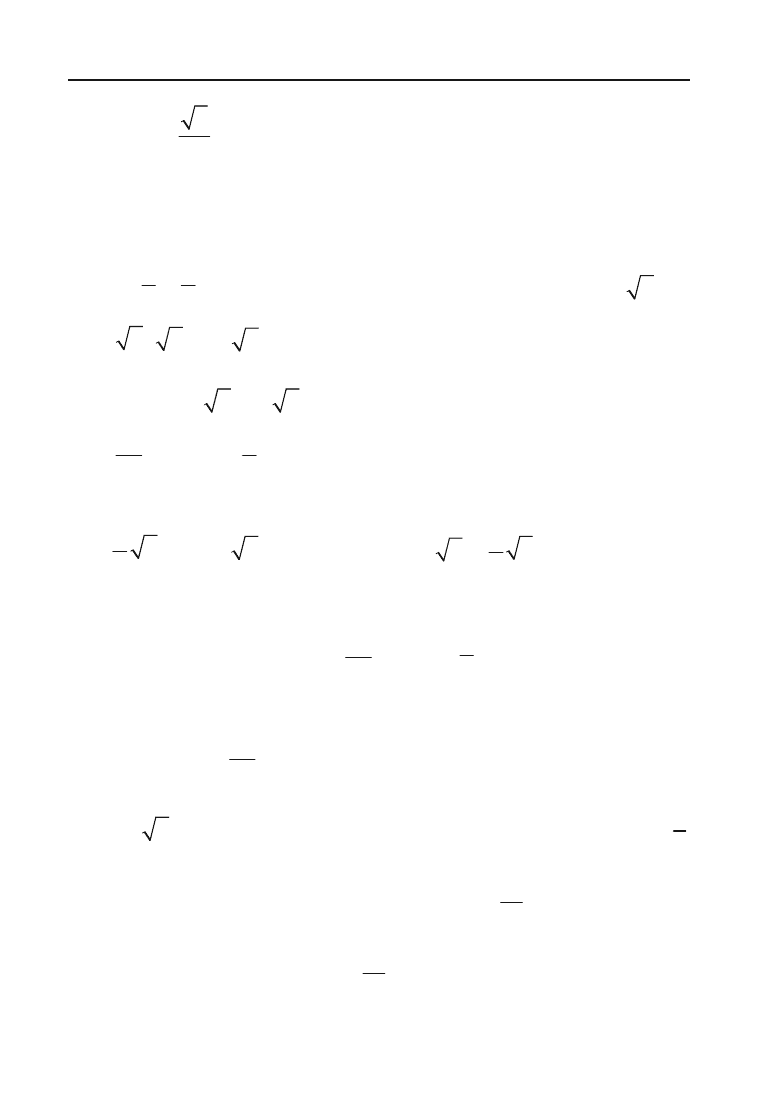
566
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
перегину (
3
2
2
;0); асимптота х = 0; 6) визначена: х
(
f
;0)
(0;
f
);
графік симетричний відносно осі ординат;
у
min
= 2 при х =
1r
; макси+
мумів немає; точок перегину немає; асимптота
х=0; 7) визначена:
х
(
f
,1)
(1;
f
); у
min
=–1 при х=0; максимумів немає; точка пере+
гину
(
1
2
;
8
9
); асимптоти х=1, у=0; 8) визначена: х
(
f
,
3
)
(
3
;
3
)
(
3
;
f
); графік симетричний відносно початку
координат;
у
max
= –4,5 при х = 3, у
min
= 4,5 при х = –3; точка перегину (0;0);
асимптоти
х=
3
, х=
3
, у=– х; 9) визначена: х
(
f
;1)
(1;
f
);
у
min
=
27
4
при х=
3
2
; максимумів немає; точка перегину (0;0);
асимптотa
х = 1; 10) визначена: х
(
f
;1)
(1;
f
); у
max
=0 при х=0,
у
min
=
3
4
4
3
при х=
3
4
; точка перегину (
3
2
;
3
2
2
3
); асимптоти х=1,
у=x; 11) визначена: х
(;)f f
; графік симетричний відносно осі
ординат;
у
max
=0 при х=0, у
min
=
27
8
при х=
1
2
r
; точка перегину (
1r
;0),
при
х
|
0,7 і х
|
0,26r
; асимптот немає; 12) визначена: х
(
f
;–1)
(–1;
f
); у
max
=
2
27
при х=5, у
min
=0 при х=1; абсциси точок переги+
ну
523
r
; асимптоти х=–1, у=0; 13) визначена: х
(;)f f
; у
max
=
1
e
при х=1, мінімумів немає; точка перегину (2;
2
2
e
); асимптота у=0;
14) визначена: х
(;)f f
; у
max
=
2
4
e
при х=2; у
min
=0 при х=0; абсциси
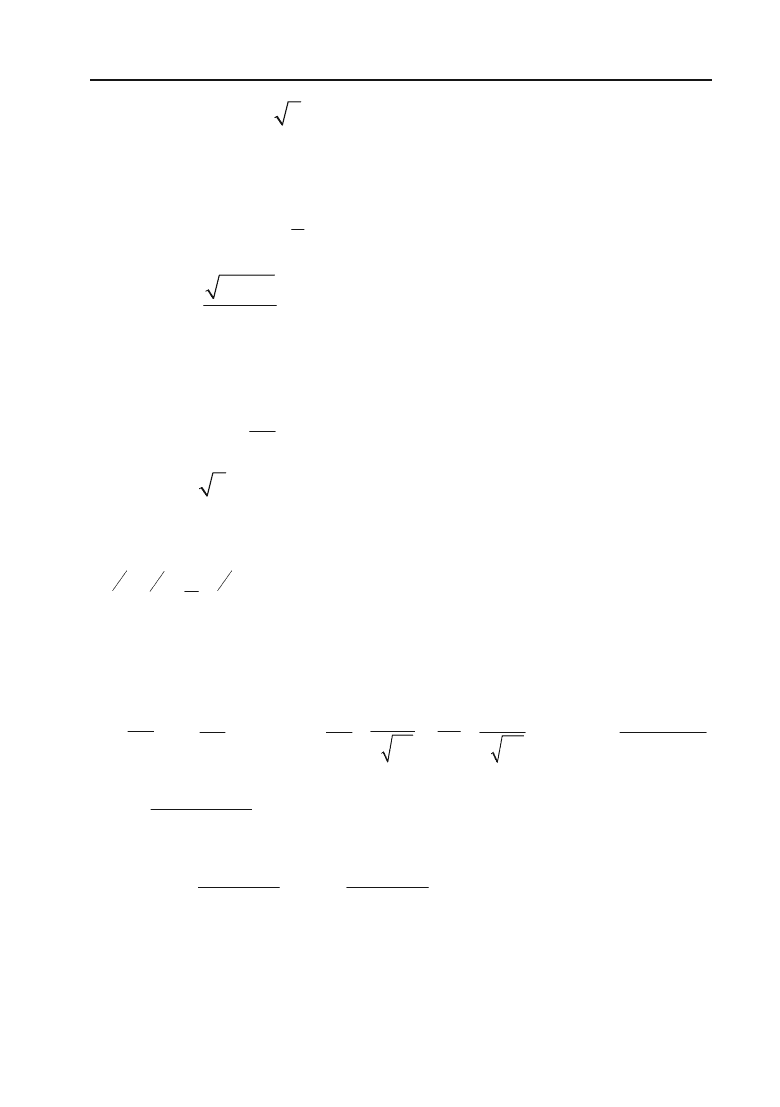
567
Відповіді до задач та прикладів
точок перегину
22
r
; асимптота у=0; 15) визначена: х
(–1,
f
);
у
min
=0 при х=0; максимумів немає; графік немає точок перегину; асим+
птота
х=–1; 16) визначена: х
(;)f f
; графік симетричний віднос+
но осі ординат
; у
max
=
1
e
при х=
1r
; у
min
=0 при х=0; абсциси точок
перегину
517
2
r
r
; асимптота у=0; 17) визначена: х
(;)f f
;
графік симетричний відносно осі ординат
; у
min
=0 при х=0; максимумів
немає; точки перегину (
1r
; ln 2); асимптот немає; 18) визначена:
х
(;)f f
; у
max
=
3
27
e
при х=3; мінімумів немає; абсциси точок пере+
гину 0
і
33
r
; асимптота у=0; 19) визначена: х
(
f
;0)
(0;
f
);
екстремумів немає
; графік немає точок перегину; асимптоти х=0, у=0,
у=–1; 20) визначена: х
(0;
f
); екстремумів немає; точка перегину
(
3
2
e
;
3
2
e
+
3
2
3
2
e
); асимптоти х=0, у=х.
Розділ V. Диференціальне числення функції багатьох змінних
5.7.
z
x
w
w
=2x,
z
y
w
w
=–3y
2
. 5.8.
z
x
w
w
=
1
2 xy
y,
z
y
w
w
=
1
2 x
y
x. 5.9.
x
z
c
=
2
1
cos ( )xy
,
y
z
c
=–
2
1
cos ( )xy
. 5.10.
x
z
c
=2xcos(x
2
+y
2
),
y
z
c
=2y cos(x
2
+y
2
).
5.11.
x
z
c
=
2
3
32
2
x
y
x
xy
,
y
z
c
=
3
2
2
x
x
xy
. 5.12.
x
z
c
=e
x–y
,
y
z
c
= –e
x
–
y
.
5.13.
x
z
c
= 2
sin(
x+y
)
ln2cos(x+y),
y
z
c
= 2
sin(
x+y
)
ln2cos(x+y). 5.14.
x
z
c
= cos x,
y
z
c
= sin y. 5.15.
x
z
c
= 2ycos xy,
y
z
c
= 2xcos xy. 5.16.
x
z
c
= –3
2xy
3
sin(x
2
y
3
),
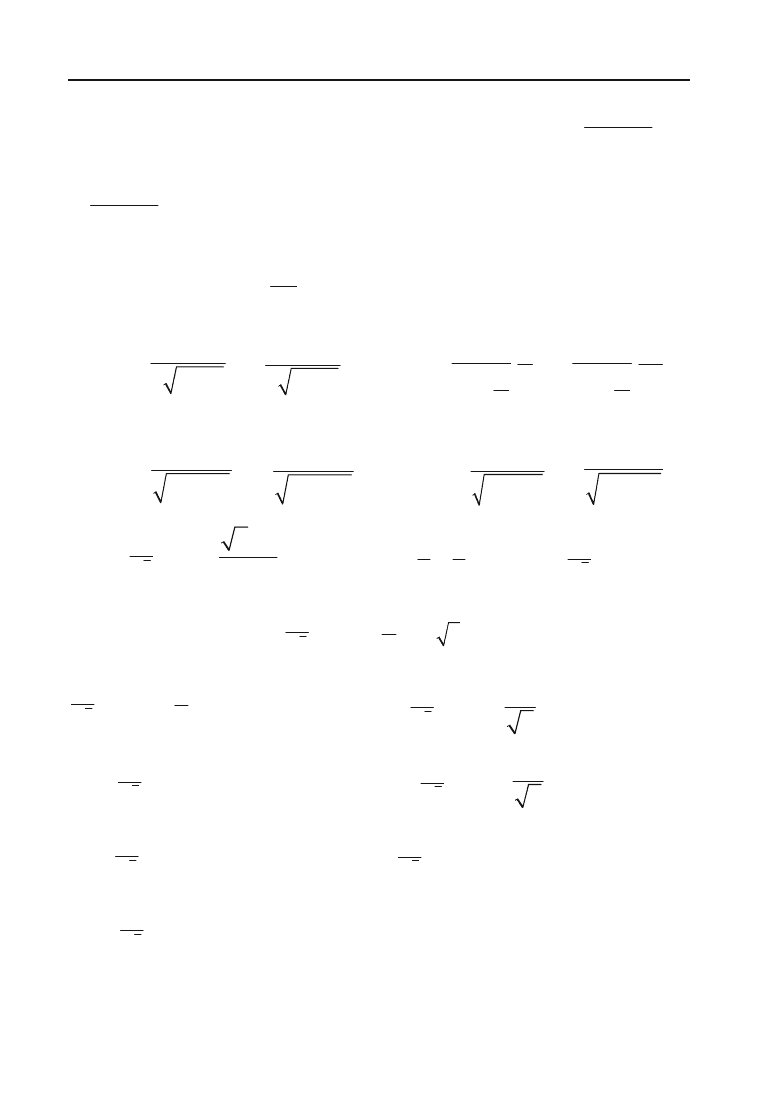
568
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
y
z
c
= –3
3x
2
y
2
sin(x
2
y
3
). 5.17. dz=2xy
4
dy + 4x
2
y
3
dy. 5.18. dz =
22
x
xy
dx+
+
22
y
xy
dy. 5.19. dz= e
x
–2
y
dx – 2e
x
–2
y
dy. 5.20. dz = cos(x–y)(ydx+xdy).
5.21. dz = 2xlnydx +
2
x
y
dy. 5.22. dz = (2xy – y
2
)dx + (x
2
–2xy)dy.
5.23. dz=
1
2 x
y
dx–
1
2 x
y
dy. 5.24. dz=
2
1
cos
x
y
1
y
dx–
2
1
cos
x
y
2
x
y
dy.
5.25. dz=
22
x
xy
dx+
22
y
xy
dy. 5.26. dz=
22
x
xy
dx–
22
y
xy
dy.
5.40.
z
l
w
w
(M
0
)=
31
4
, gradz|
0
M
=
11
;
22
§·
¨¸
©¹
. 5.41.
z
l
w
w
(M
0
) = 6,
grad
z|
0
M
= (0;12). 5.42.
z
l
w
w
(M
0
) =
3
2
(3–
3
), gradz|
0
M
= (9;–3). 5.43.
z
l
w
w
(M
0
)=
6
5
, gradz|
0
M
= (–2;0). 5.44.
z
l
w
w
(M
0
) =
1
2
, gradz|
0
M
= (2;3).
5.45.
z
l
w
w
(M
0
) = 0, gradz|
0
M
= (24;0). 5.46.
z
l
w
w
(M
0
) =
7
2
, gradz|
0
M
= (4;3).
5.47.
z
l
w
w
(M
0
) = 0, gradz|
0
M
= (0;0). 5.48.
z
l
w
w
(M
0
)= –20, gradz|
0
M
= (–20;–12).
5.49.
z
l
w
w
(M
0
) = 12, gradz|
0
M
= (–13;–12). 5.54.
max
(20;30) 500zz
.
5.55.
max
(10;50) 2850zz
. 5.56.
max
(40;30) 700zz
.
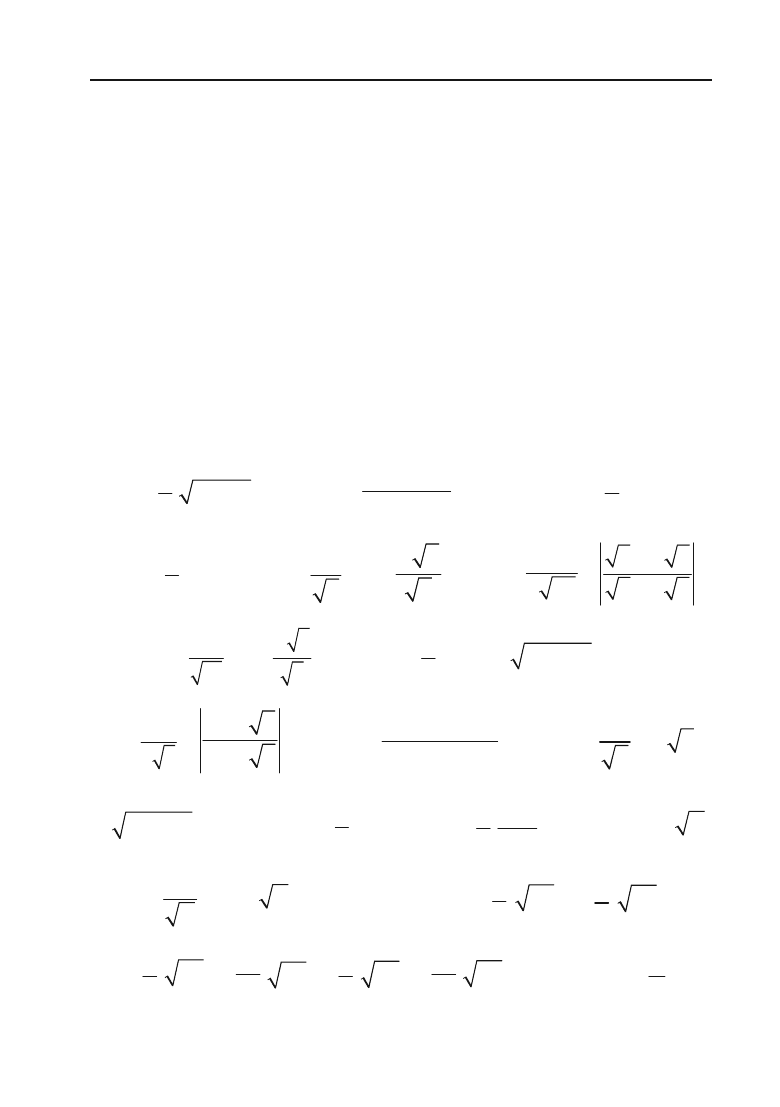
569
Відповіді до задач та прикладів
5.57.
max
(20;50) 800zz
. 5.58.
max
(20;40) 300zz
.
5.59.
max
(10;40) 200zz
. 5.60.
max
(50;20) 900zz
.
5.61.
min
(2;2) 4zz
;
max
(2;2) 4zz
. 5.62.
min
(1;1) 2zz
.
5.63.
min
( 3/2; 3/2) 19/4zz
. 5.65. y = 1,525x – 0,12.
5.67. y = –2,186x + 2,92. 5.67. у = 3,46х + 2,86. 5.68. у = 15,93х + 110,57.
5.73. П(240;340/3) = 26866,67. 5.74. П(10;5) = 475. 5.75. 1) E
x
(z)
|
0,042;
E
y
(z)
|
0,958; 2) E
x
(z)
|
0,911; E
y
(z)
|
1,821; 3) E
x
(z) = 1; E
y
(z) = 1;
4) E
x
(z)
|
0,363; E
y
(z)
|
0,545. 5.76. x
1
= 9994, x
2
= 3. 5.78. 25; 50.
Розділ VI. Інтегральне числення
6.14.
2
7
37
x
+ C. 6.15.
1
3(7 3 )
x
+ C. 6.16. C –
1
3
ln|7 – 3x|.
6.17. C–
1
6
ln|5–3x
2
|. 6.18.
1
7
arcsin
7
3
x
+C. 6.19.
1
235
ln
57
57
x
x
+
+ C. 6.20.
1
15
arctg
5
3
x
+ C. 6.21.
1
3
ln|
2
395xx
| + C.
6.22.
1
47
ln
27
27
x
x
+ C. 6.23.
22
1
12(5 3 )
x
+ C. 6.24.
1
7
ln|x
7
+
+
2
74x
| + C. 6.25. C –
1
5
e
–5
x
. 6.26. C –
1
3
3
7
ln7
x
. 6.27. C – 2cos
x
.
6.28.
4
x
+ 18
6
x
+ 5ln|x| + C. 6.29.
6
7
6
7
x
–
4
3
4
3
x
+ C.
6.30.
3
2
3
2
x
+
18
7
6
7
x
+
9
5
3
5
x
+
6
13
6
7
x
+ C. 6.31. e
x
+
1
x
+ C.
570
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.32.
ln
x
a
a
+
2
x
+ C. 6.33. –ctg
2
x – tg
2
x + C. 6.34.
3
3
x
+
2
x
+ C.
6.35.
3
2
ln|x
2
–4| – ln
2
2
x
x
+ C. 6.36. –
2
1
x
+ arcsinx + C.
6.37. tg
2
x – ctg
2
x + C. 6.38.
1
2
x –
1
2
sin x + C. 6.39.
1
2
x +
3
4
sin
2
3
x
+ C.
6.40. 2arctg x – 3arcsin x + C. 6.41.
3
5
arctg
5
x
– ln|
2
5
xx
| + C.
6.42.
2
2
x
–
2
3
3
x
+ x + C. 6.43. –2cos x +
3
3
x
+ C. 6.44.
2
(2)
2
x
+ C.
6.45.
5
2
ln|x
2
+4| – arctg
2
x
+ C. 6.46.
2
1x
+ ln|
2
1
xx
| + C.
6.47. x – arctgx + C. 6.48.
3
3
x
+ 3x +
33
2
ln
3
3
x
x
+ C.
6.49.
1
2
(
32ln
)
x
+ C. 6.50.
2
arctg
2
x
+ 2arctg x + C. 6.56. C –
–
ln | | 1
x
x
. 6.57. C –
1
4
e
–2
x
(2x + 1). 6.58.
3
4
3
4
x
(ln|x|–1) + С.
6.59.
1
3
xsin 3x +
1
9
cos 3x + C. 6.60. –x
ctg x + ln |sin x| + C.
6.61. 4sin
2
x
– 2xcos
2
x
+ C. 6.62. C –
2
ln
x
x
–
2ln
x
x
–
2
x
.
6.63.
1
32
cos 4x +
8
x
sin 4x –
2
4
x
cos 4x + C. 6.64. –2
2
x
e
(x
2
+ 4x + 8) + C.
