Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


521
Розділ VIII. Ряди
lim
nof
1
1
n
n
n
n
ax
ax
= |x|
lim
n
of
1
n
n
a
a
= |x|
L.
Звідси за ознакою Даламбера ряд (8.24) збігається при |
x|
L < 1 і
розбігається при |
x|
L > 1. Отже, якщо |x| <
1
L
, то ряд (8.24) збігаєть+
ся, а якщо |
x| >
1
L
, то розбігається. Таким чином радіус збіжності
степеневого ряду визначається формулою
R =
1
L
=
lim
n
of
1
n
n
a
a
. (8.26)
Якщо до ряду застосовується ознака Коші, то, міркуючи аналог+
ічно, одержуємо наступну формулу
R =
1
L
=
1
lim | |
n
n
n
a
of
. (8.27)
Формулами (8.26) і (8.27) виражається і радіус збіжності ряду
(8.25). Інтервалом збіжності цього ряду є (
х
0
– R; x
0
+ R).
Таким чином, будь+який степеневий ряд має радіус збіжності
R і
інтервал збіжності (
–R; R). При х =
r
R ряд може або збігатися, або
розбігатися. Це питання розв’язується для кожного конкретного ряду
індивідуально. Отже, областю збіжності степеневого ряду (8.34) є
його інтервал збіжності з можливим приєднанням до нього однієї
або двох точок в залежності від того, як веде себе ряд на кінцях інтер+
валу, тобто при
х =
r
R.
8.4.1. Розв’язання прикладів
Приклад 8.22. Знайти область збіжності ряду
1
1
(1)
n
n
n
x
n
f
¦
= х –
2
2
x
+
3
3
x
– ... + (–1)
n–1
n
x
n
+ ...
Розв’язок. За формулою (8.26) знайдемо радіус збіжності
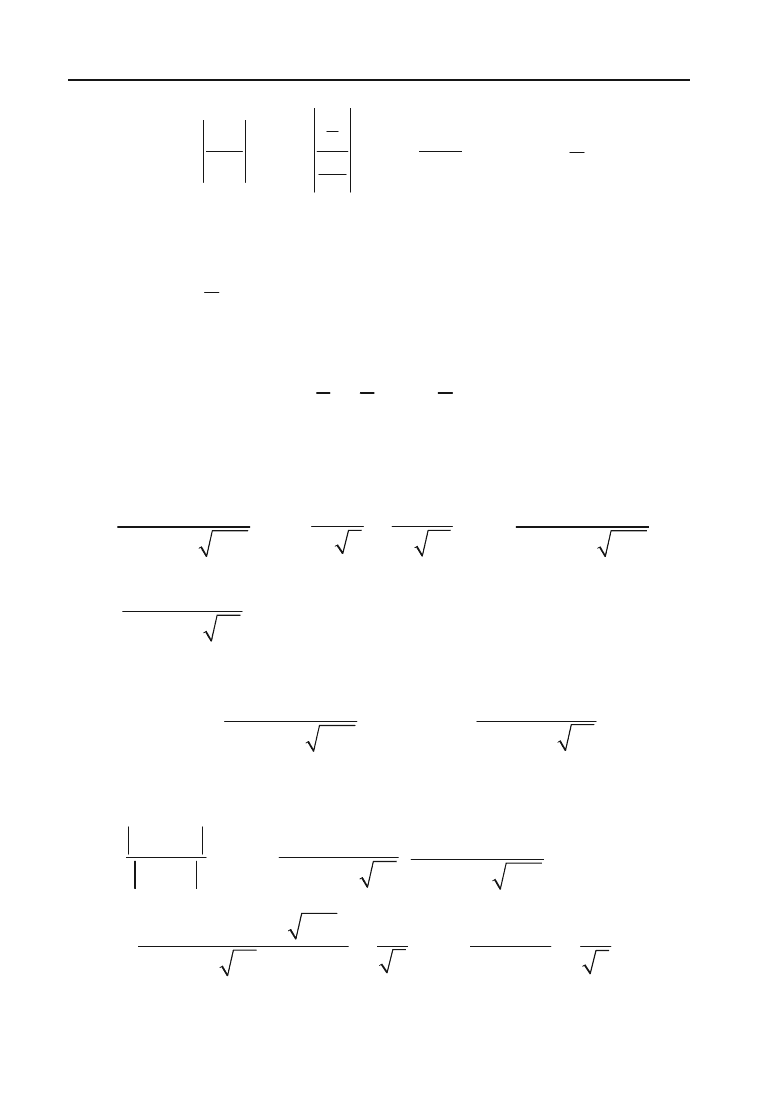
522
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
R =
lim
n
of
1
n
n
a
a
=
lim
nof
1
1
1
n
n
=
lim
nof
1n
n
=
lim
nof
(1 +
1
n
) = 1.
Отже, інтервалом збіжності ряду буде (–1; 1). Розглянемо
збіжність ряду на кінцях інтервалу збіжності. При х = 1 одержуємо
ряд
1
1
1
(1)
n
n
n
f
¦
. Цей знакопереміжний ряд за ознакою Лейбніца
збігається неабсолютно. При х = –1 одержуємо ряд
–1 –
1
2
–
1
3
– ... –
1
n
– ...
який розбігається. Отже, областю збіжності ряду є проміжок (–1;1].
Приклад 8.23. Знайти радіус та область збіжності ряду
11
21
1
2
(2 1) 3
nn
n
n
x
n
f
¦
= 1 +
2
2
33
x
+
22
4
53
x
+ ... +
11
21
2
(2 1) 3
nn
n
x
n
+
+
2
2
(2 1) 3
nn
n
x
n
+ ...
Розв’язок. Маємо
U
n
(x) =
11
21
2
(2 1) 3
nn
n
x
n
; U
n+1
(x) =
2
2
(2 1) 3
nn
n
x
n
.
В силу ознаки Даламбера заданий степеневий ряд буде збіжним
для тих значень, для яких
lim
nof
1
()
()
n
n
Ux
Ux
=
lim
n
of
2
2| |
(2 1) 3
nn
n
x
n
:
11
21
2||
(2 1) 3
nn
n
x
n
=
=
lim
n
of
21
211
2| |(2 1) 3
(2 1) 3 2 | |
nn
nn n
xn
nx
=
2
3
|x|
lim
nof
2
2
(2 1)
(2 1)
n
n
=
2
3
|x|
1 < 1,
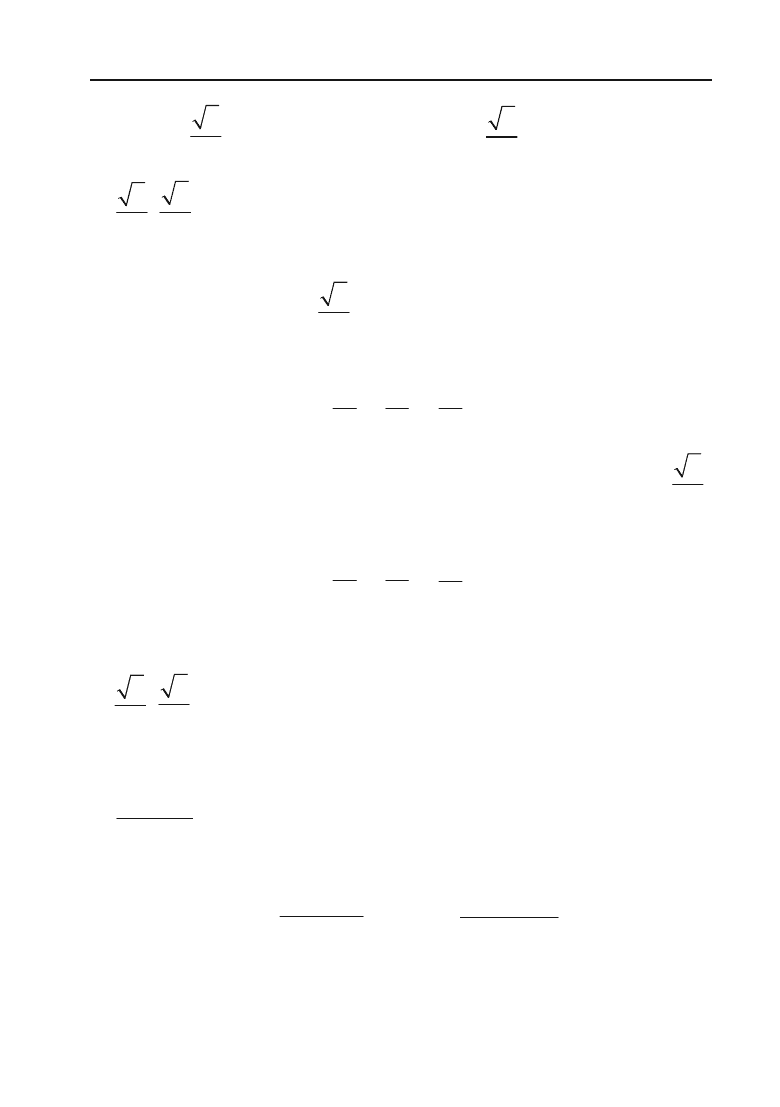
523
Розділ VIII. Ряди
тобто |x| <
3
2
. Отже, радіус збіжності R =
3
2
, а інтервал збіжності
(
3
2
;
3
2
).
Тепер з’ясуємо поведінку ряду на кінцях інтервалу збіжності.
В лівому кінці, при
х =
3
2
, заданий степеневий ряд перетворюєть+
ся в числовий ряд
1 –
2
1
3
+
2
1
5
–
2
1
7
+ ...,
який збігається за ознакою Лейбніца. В правому кінці, при
х =
3
2
,
одержуємо ряд
1 +
2
1
3
+
2
1
5
+
2
1
7
+ ...,
який збігається.
Таким чином, заданий степеневий ряд збігається на відрізку
[
3
2
;
3
2
].
Приклад 8.24. Знайти область збіжності степеневого ряду
3
2
1
(8)
n
n
x
n
f
¦
.
Розв’язок. Маємо
U
n
=
3
2
(8)
n
x
n
; U
n+1
=
33
2
(8)
(1)
n
x
n
.
Знайдемо
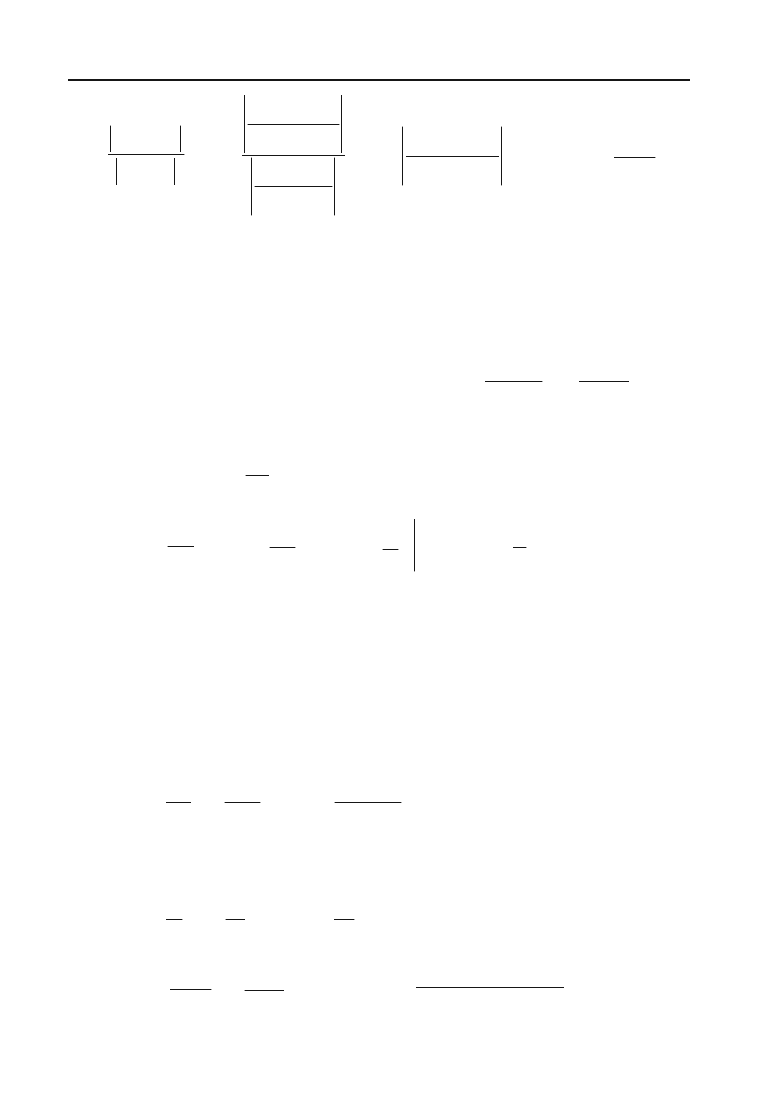
524
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
lim
nof
1
()
()
n
n
Ux
Ux
=
lim
nof
33
2
3
2
(8)
(1)
(8)
n
n
x
n
x
n
=
lim
nof
23
2
(8)
(1)
nx
n
= |x + 8|
3
lim
nof
2
1
n
n
§·
¨¸
©¹
=
= |
x + 8|
3
1 < 1.
Звідки
|x + 8|
3
< 1, |x + 8| < 1, –1 < x + 8 <1, –9 < x < –7.
Дослідимо межі інтервалу. При
х = –9 одержуємо числовий зна+
копереміжний ряд з загальним членом
a
n
=
3
2
(1)
n
n
=
2
(1)
n
n
, який
збігається згідно ознаки Лейбніца. При
х = –7 одержуємо ряд з додат+
ними членами
a
n
=
2
1
n
. Досліджуючи його за інтегральною ознакою
2
1
dx
x
f
³
=
lim
nof
2
1
dx
x
f
³
=
lim
bof
(
1
x
)
1
b
=
lim
bof
(
1
b
+ 1) = 1,
з’ясуємо, що він збігається. Отже, областю збіжності заданого ряду є
відрізок [–9; –7].
8.4.2. Приклади для самостійного розв’язку
8.25. Знайти область збіжності степеневих рядів:
а) 10
x + 100x
2
+ ... + 10
n
x
n
+ ...;
б)
x +
2
20
x
+
3
300
x
+ ... +
1
10
n
n
x
n
+ ...;
в) 1 +
x + 2!x
2
+ ... + n!x
n
+ ...;
г) 1 + 2
x
2
+ 4x
4
+ ... + 2
n–1
x
2(n–1)
+ ...;
д) 1 +
1
1!
x +
2
2!
x
2
+ ... +
!
n
n
x
n
+ ...;
ж)
x –
3
33!
x
+
5
55!
x
– ... + (–1)
n–1
21
(2 1) (2 1)!
n
x
nn
+ ... .

525
Розділ VIII. Ряди
§ 8.5. Розклад функцій в ряди Тейлора і Маклорена
8.5.1. Розклад функцій в ряди Тейлора
Рядом Тейлора для функції f(x) при умові, що вона визначена
в околі точки
а, і в цій же точці має скінчені похідні будь+якого по+
рядку, називається степеневий ряд вигляду:
f(a) +
()
1!
fa
c
(x – a) +
()
2!
fa
cc
(x – a)
2
+ ... +
(1)
()
(1)!
n
f
a
n
(x – a)
n–1
+... . (T)
Функція
f(x) буде сумою цього ряду тільки для тих значень х,
при яких залишковий член
R
n
(x) =
()
(())
!
n
f
axa
n
4
(x – a)
n
, де
0 <
Q < 1, формули Тейлора
f(x) = f(a) +
()
1!
fa
c
(x – a) +
()
2!
fa
cc
(x – a)
2
+ ... +
(1)
()
(1)!
n
f
a
n
(x – a)
n–1
+
+
()
(()
!
n
f
axa
n
4
(x – a)
n
,
має свою границю нуль, коли
n of
, тобто
lim
n
of
R
n
(x) = 0.
Коротко: необхідною і достатньою умовою існування рівності
f(x) = f(a) +
()
1!
f
a
c
(x – a) +
()
2!
f
a
cc
(x – a)
2
+ ... +
(1)
()
(1)!
n
f
a
n
(x – a)
n–1
+ ... (Т)
для значень
х із деякого проміжку є умова
lim
nof
R
n
(x) = 0 для всіх х
із цього проміжку. Формула (Т), що вірна при вказаній умові, дає
розклад функції
f(x) в ряд Тейлора. Таким чином, функція f(x) може
бути розкладена в ряд Тейлора для розглянутого
х, якщо:
а) вона має похідні будь+якого порядку,
б) границя залишкового члена при
n of
дорівнює нулю, тобто
lim
nof
R
n
(x) = 0.
Для розкладу заданої функції в ряд Тейлора необхідно:

526
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
8.5.2. Розклад функції в ряд Маклорена
Якщо в ряді Тейлора (Т) прийняти а = 0, то одержимо ряд Мак+
лорена:
f(x) = f(0) +
(0)
1!
f
c
x +
(0)
2!
f
cc
x
2
+ ... +
(1)
(0)
(1)!
n
f
n
x
n–1
+ ... (М)
Розглянемо розклад в степеневий ряд (ряд Маклорена) деяких
елементарних функцій.
1) f(x) = e
x
.
Маємо:
f(x) = e
x
; f(0) = 1;
()
f
x
c
= e
x
;
(
0
)
f
c
= 1;
()
f
x
cc
= e
x
;
(0)f
cc
= 1;
............................... ..........................
f
(n)
(x) = e
x
; f
(n)
(0) = 1.
За формулою (М) складемо ряд Маклорена
1) записати ряд Тейлора для заданої функції, тобто обчислити
значення цієї функції і її похідні при
х = а і підставити їх у загаль+
ний вираз ряду Тейлора (Т) для заданої функції.
2) дослідити залишковий член
R
n
формули Тейлора для заданої
функції і визначити сукупність значень
х, при яких одержаний ряд
збігається до заданої функції (тобто при яких
lim
n
of
R
n
(x) = 0).
Для багатьох функцій, які використовуються в практичних зас+
тосуваннях математичного аналізу, інтервал збіжності ряду Тейлора
співпадає з сукупністю тих значень
х, при яких відповідний залиш+
ковий член
R
n
o
0, коли
n of
, тобто для багатьох функцій кожна
точка
х збіжності ряду Тейлора є і точкою збіжності того ряду, який
складено для заданої функції. Через це при розкладі багатьох функцій
в ряд Тейлора можна замість дослідження відповідного залишкового
члена
R
n
(x), де в багатьох випадках складно, дослідити збіжність са+
мого ряду Тейлора, як звичайного степеневого ряду.

527
Розділ VIII. Ряди
1 + х +
2
2!
x
+
3
3!
x
+ ... +
!
n
x
n
+ ...
Знайдемо радіус збіжності одержаного ряду
R =
lim
nof
1
n
n
a
a
=
lim
nof
(
1
)
!
!
n
n
=
lim
nof
(n + 1) =
f
.
Отже, одержаний ряд абсолютно збігається на всій числовій
прямій. Він збігається до функції
е
х
при будь+якому х
(
;f f
), так
як на будь+якому відрізку функція
е
х
та її похідні обмежені одним і
тим же числом, наприклад
е
0
.
Таким чином, при будь+якому х має місце розклад
е
х
= 1 + х +
2
2!
x
+
3
3!
x
+ ... +
!
n
x
n
+ ... (8.28)
2) f(x) = sin x.
Маємо:
f(x) = sin x; f(0) = 0;
()
f
x
c
= cos x = sin(x +
2
S
);
(0)f
c
= 1;
()
f
x
cc
= –sin x = sin(x + 2
2
S
);
(
0
)
f
cc
= 0;
()
f
x
ccc
= –cos x = sin(x + 3
2
S
);
(0)f
ccc
= –1;
f
ІV
(x) = sin x = sin(x + 4
2
S
); f
ІV
(0) = 0;
............................... ..........................
f
(n)
(x) = sin(x + n
2
S
); f
(n)
(0) =
1
0, 2
(
1
)
, 2 1
n
я
к
щ
оn m
якщо n m
®
¯
.
За формулою (М) для функції sin x складемо ряд Маклорена:
х –
3
3!
x
+
5
5!
x
+
7
7!
x
+ ... + (–1)
n–1
21
(2 1)!
n
x
n
+ ...
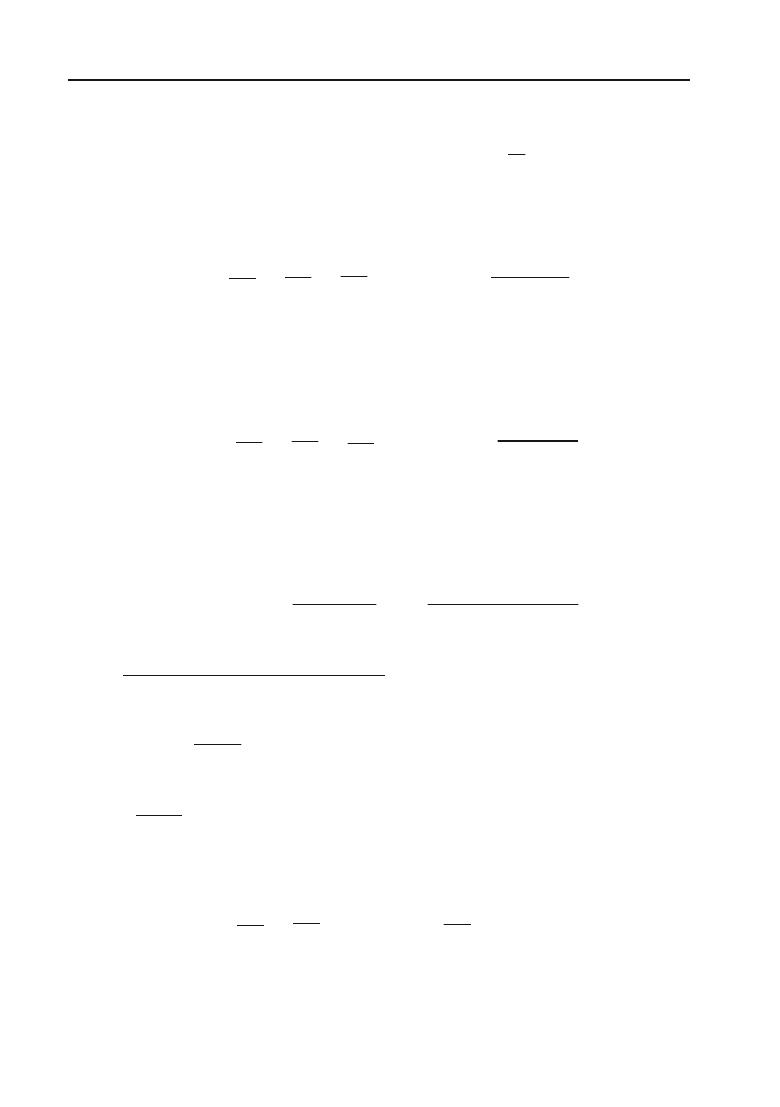
528
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Легко показати, що ряд збігається абсолютно на всій числовій
прямій, тобто
R =
f
. Так як |f
(n)
(x)| = |sin(x + n
2
S
)|
d
1, то одержа+
ний числовий ряд збігається до функції sin
x. Отже, для будь+якого
х справедливий розклад:
sin
x = х –
3
3!
x
+
5
5!
x
+
7
7!
x
+ ... + (–1)
n–1
21
(2 1)!
n
x
n
+ ... (8.29)
3) f(x) = cos x.
Аналогічно попередньому можна одержати розклад функції cos x
в ряд Маклорена, який справедливий при будь+якому х.
cos
x = 1 –
2
2!
x
+
4
4!
x
–
6
6!
x
+ ... + (–1)
n–1
22
(2 2)!
n
x
n
+ ... (8.30)
Вкажемо розклад у ряд Маклорена і інших функцій, які викори+
стовуються найчастіше.
4) f(x) = (1 + x)
m
.
(1 + x)
m
= 1 + mx +
(1)
2!
mm
x
2
+
(1)(2)
3!
mm m
x
3
+ ... +
+
(
1
)(
2
)
...
(
1
)
!
mm m m n
n
x
n
+ ..., де х
(–1; 1).
5) f(x) =
1
1 x
.
1
1 x
= 1 – x + x
2
– x
3
+ ... + (–1)
n
x
n
+ ..., де х
(–1; 1).
6) f(x) = ln(1 + x).
ln(1 + x) = x –
2
2
x
+
3
3
x
– ... + (–1)
n+1
n
x
n
+ ..., де х
(–1; 1).
7) f(x) = arctg x.

529
Розділ VIII. Ряди
arctg x = x –
3
3
x
+
5
5
x
– ... + (–1)
n+1
21
21
n
x
n
+ ..., де х
(–1; 1).
Два степеневих ряда можна почислено додавати і множити (за
правилом множення многочленів). При цьому інтервалом збіжності
одержаного нового степеневого ряду буде сукупність всіх точок, в
яких одночасно збігаються обидва ряди. Степеневий ряд в інтервалі
його збіжності можна почленно інтегрувати, а в середині інтервалу
збіжності можна почленно диференціювати.

530
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
8.5.3. Розв’язання прикладів
Приклад 8.26. Розкласти в ряд Тейлора функцію f(x) =
1
x
при
а = –2.
Розв’язок. Обчислимо значення заданої функції і її похідних при
х = а = –2.
f(x) = x
–1
; f(–2) =
1
2
;
()
f
x
c
= –1x
–2
;
(
2
)
f
c
=
2
1!
2
;
()
f
x
cc
= 1
2x
–3
;
(
2
)
f
cc
=
3
2!
2
;
()
f
x
ccc
= –1
23x
–4
;
(
2
)
f
ccc
=
4
3!
2
;
f
ІV
(x) = 1
2
3
4x
–5
; f
ІV
(–2) =
5
4!
2
;
........................... .................................
f
(n)
(x) = (–1)
n
n!x
n–1
; f
(n)
(–2) =
1
!
2
n
n
.
Підставимо ці значення в ряд Тейлора (Т) для заданої функції,
одержуємо:
1
x
=
1
2
–
2
1!
21!
(х + 2) –
3
2!
22!
(х + 2)
2
–
4
3!
23!
(х + 2)
3
– ... –
–
1
!
2!
n
n
n
(х + 2)
n
– ... = –
1
2
(1 +
2
2
x
+
2
2
(2)
2
x
+
3
3
(2)
2
x
+
+ ... +
(2)
2
n
n
x
+ ...).
