Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

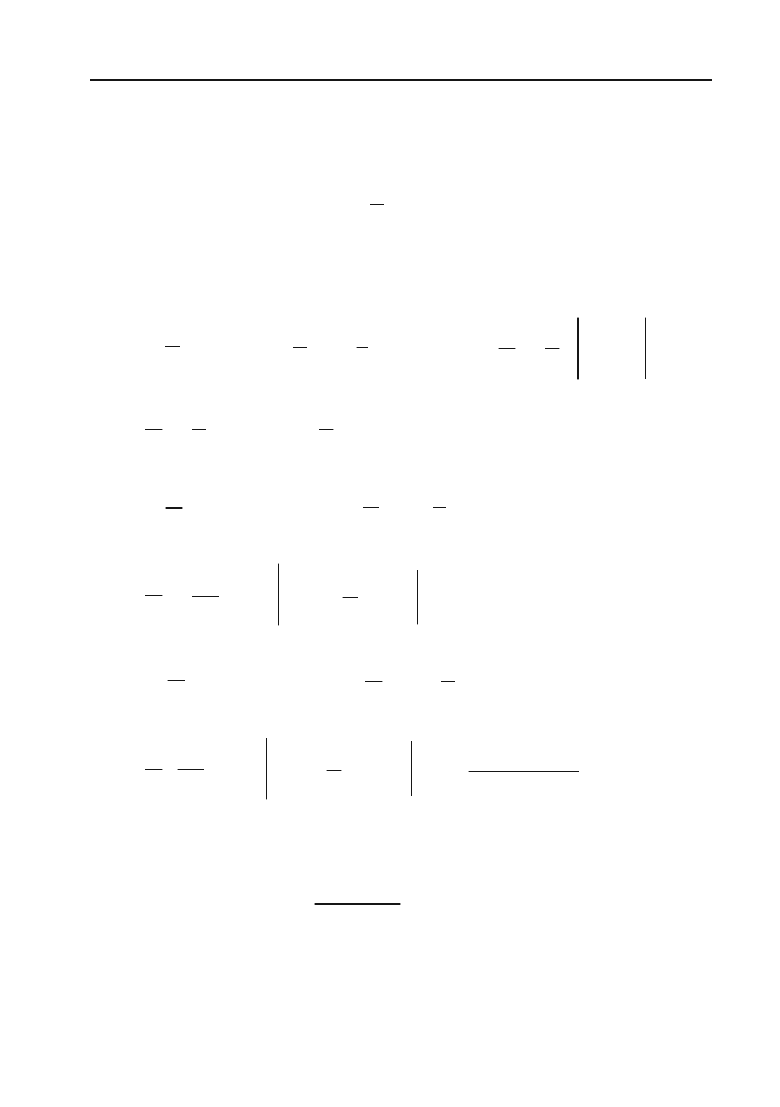
541
Розділ VIII. Ряди
8.7.2. Розв’язання прикладів
Приклад 8.42. Розкласти в ряд Фур’є функцію
1
, ( 0)
()
2
1, (0 )
x
fx
x
S
S
°
®
°
d
¯
.
Розв’язок. Обчислимо коефіцієнти Фур’є функції f(x):
а
0
=
1
()
f
xdx
S
S
S
³
=
0
0
11
1
2
dx dx
S
S
S
§·
§·
¨¸
¨¸
©¹
©¹
³³
=
1
S
(
1
2
х
0
S
+ х
0
S
) =
=
1
S
(
1
2
S
+
S
) =
1
2
;
а
n
=
1
()cosfx nxdx
S
S
S
³
=
0
0
11
cos 1cos
2
nxdx nxdx
S
S
S
§·
§·
¨¸
¨¸
©¹
©¹
³³
=
=
1
S
(
1
2n
sin nx
0
S
+
1
n
sin nx
0
S
) = 0;
b
n
=
1
()sinfx nxdx
S
S
S
³
=
0
0
11
sin 1sin
2
nxdx nxdx
S
S
S
§·
§·
¨¸
¨¸
©¹
©¹
³³
=
=
1
S
(
1
2n
cos nx
0
S
–
1
n
cos nx
0
S
) =
3(1 ( 1) )
2
n
n
S
;
так як
cos
n
S
= (–1)
n
, то
b
2k
= 0, (k = 1, 2, 3, …),
b
2k+1
=
3
(2 1)k
S
, (k = 1, 2, 3, …).
Функція
f(x) задовольняє умовам Дирихле, а через це розкла+
дається в свій ряд Фур’є. Отже, в кожній точці неперервності:
542
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
f(x) =
1
4
+
0
3sin(21)
21
k
kx
k
S
f
¦
.
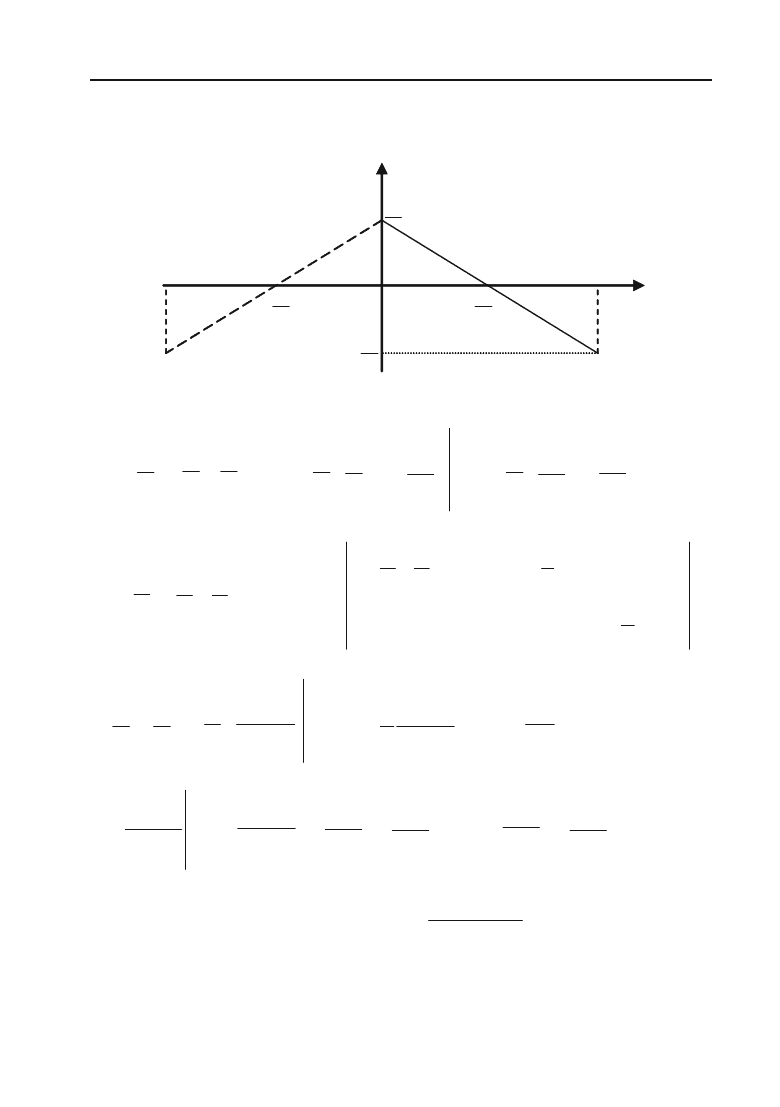
Приклад 8.43. Розкласти в ряд Фур’є функцію f(x) = x (–
S
< x <
S
).
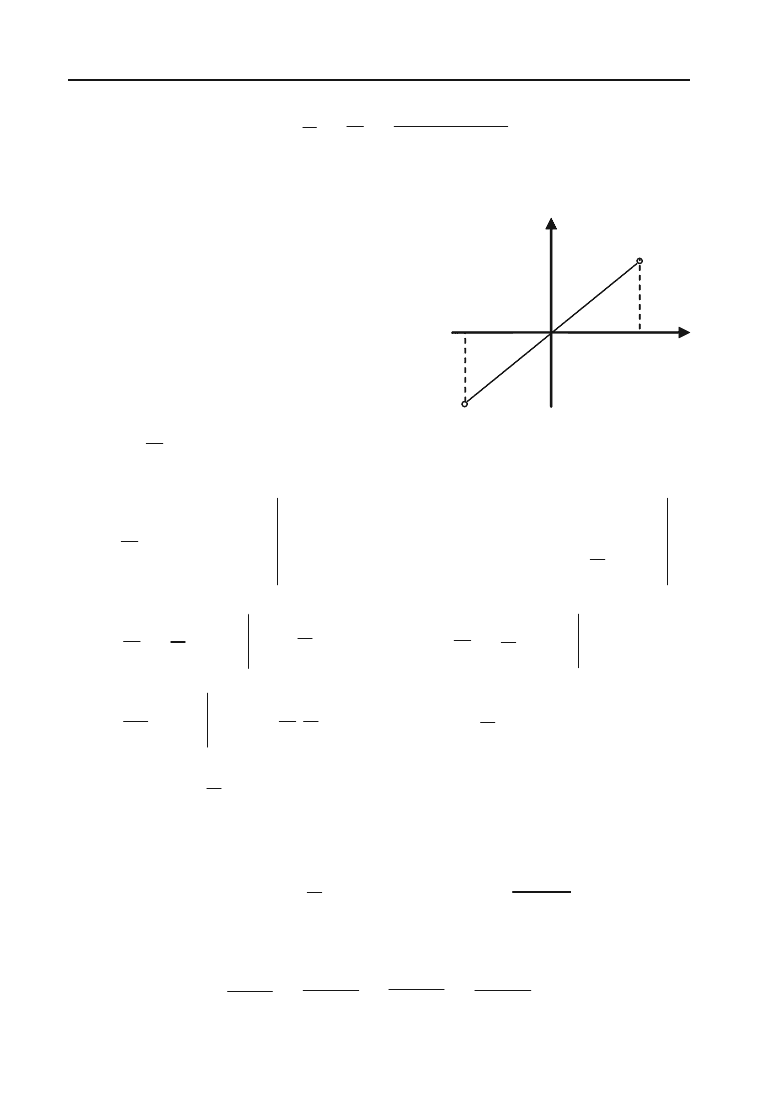
Розв’язок. Задана функція задоволь+
няє умовам Дирихле і через це може
бути розкладена в ряд Фур’є. На інтер+
валі (
–
S
< x <
S
) функція f(x) = x —
непарна (див. рис. 8.1). Звідси слідує, що
ряд Фур’є цієї функції буде містити
тільки синуси.
Знайдемо
b
n
.
b
n
=
0
2
()sinfx nxdx
S
S
³
=
=
0
2
sin
x
nxdx
S
S
³
=
,
1
sin , sin cos
u x du dx
dv nxdx v nxdx nx
n
³
=
=
2
S
(
1
n
cos nx
0
S
+
1
n
0
cosnxdx
S
³
) =
2
S
(
1
n
cos nx
0
S
+
+
2
1
n
sin nx
0
S
) =
2
S
1
n
S
(–1)
n
= (–1)
n+1
2
n
;
b
n
= (–1)
n+1
2
n
.
Отже,
x =
1
1
2
(1) sin
n
n
nx
n
f
¦
= 2
1
1
sin
(1)
n
n
nx
n
f
¦
.
В розгорнутому вигляді, надаючи
n значення 1, 2, 3, ... , одержуємо:
x = 2(
sin
1
x
–
sin 2
2
x
+
sin3
3
x
–
sin 4
4
x
+ …).
Y
S
0
S
X
Рис. 8.1.

543
Розділ VIII. Ряди
В інтервалі (–
S
;
S
) ця функція має місце в точках непервності
функції
f(x), тобто в даному випадку у всіх внутрішніх точках інтер+
валу (–
S
;
S
). Поза інтервалом цей ряд зображає періодичне провод+
ження розглянутої функції.
В точках же розриву, якими являються точки
S
r
,
3
S
r
, ..., сума
ряду дорівнює середньому арифметичному її лівосторонньої та пра+
восторонньої границі в цих точках.
Знайдемо ці границі. Наприклад, в точці
х =
S
.
0
lim
x
S
o
f(x) =
0
lim
x
S
o
x =
S
;
0
lim
x
S
o
f(x) =
0
lim
x
S
o
x = –
S
.
Середнє арифметичне цих границь:
(0)(0)
0
22
ff
SSSS
.
У всіх точках розриву цієї функції одержуємо те ж саме. Таким
чином, в точках розриву сума ряду буде дорівнювати нулю. Отже,
одержаний розклад можна записати і так:
2(
sin
1
x
–
sin 2
2
x
+
sin3
3
x
–
sin 4
4
x
+ …) =
,
0,
(
21
)
xякщо x
якщо x k
SS
S
®
¯
де k — будь+яке ціле число.
Приклад 8.44. Розкласти в ряд Фур’є функцію f(x) = |x| (–
S
< x
d
S
).
Розв’язок. Це неперервна функція з періодом
2
S
, задовольняє
умовам розкладу в ряд Фур’є, вона парна. Знаходимо:
a
0
=
2
S
0
()
f
xdx
S
³
=
2
S
0
xdx
S
³
=
2
S
2
0
2
x
S
=
S
;
a
n
=
2
S
0
()cos
f
xnxdx
S
³
=
2
S
0
cosxnxdx
S
³
=
=
1
,
cos , cos sin
n
u x du dx
dv nxdx v nxdx nx
³
=
544
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
=
2
S
(x
1
n
sin nx
0
S
–
2
S
0
sinnxdx
S
³
) =
2
S
(0 +
2
1
n
cos nx
0
S
) =
=
2
2
n
S
(cos np – 1) =
2
0,
4
,
я
кщо n парне
я
кщо n непарне
n
S
°
®
°
¯
.
Отже,
|x| =
2
S
–
4
S
(cos x +
1
9
cos 3x +
1
25
cos 5x + …+
2
1
(
21
)
n
cos(2n + 1)x + …).
Приклад 8.45. Розкласти в ряд Фур’є функцію f(x)=x, що задана
на інтервалі
(0;
2
S
).
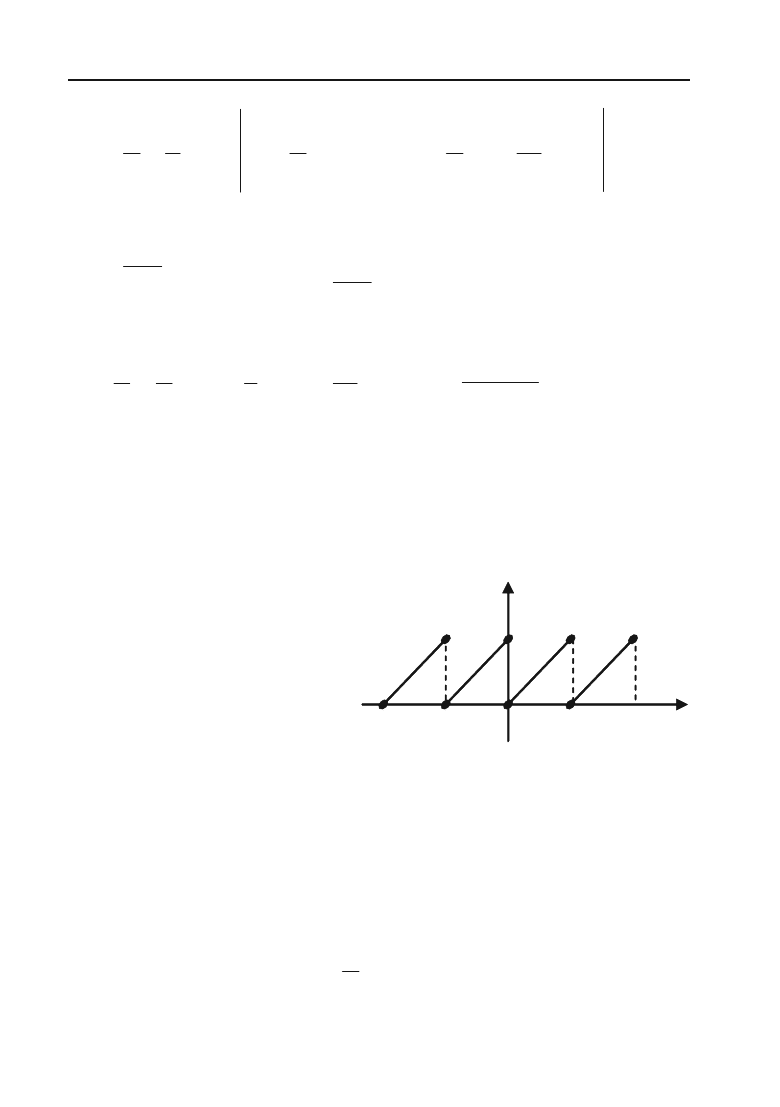
Розв’язок. На рис. 8.2 показано графік заданої функції з її періо+
дичним продовженням. Аналітичний вираз функції співпадає з ана+
літичним виразом функції в задачі 8.43. проте між ними маємо істот+
ну відмінність. В задачі 8.43
функція
f(x) = x задавалась
на інтервалі (–
S
;
S
), а в цій
задачі на інтервалі (0;
2
S
). Їх
відмінність легко бачити із
графіків функцій. Функція
f(x)= x на інтервалі (0;
2
S
)
не належить а ні до класу
парних, а ні до класу непар+
них.
Якщо функція
f(x) задана не в інтервалі (–
S
;
S
), а в інтервалі
(0;
2
S
), також довжиною
2
S
, то її можна розкласти в ряд Фур’є
того ж виду, що і (8.36), але коефіцієнти визначаються за форму+
лами:
а
0
=
2
0
1
()fxdx
S
S
³
;
Y
4
S
2
S
0
2
S
4
S
Х
Рис. 8.2.
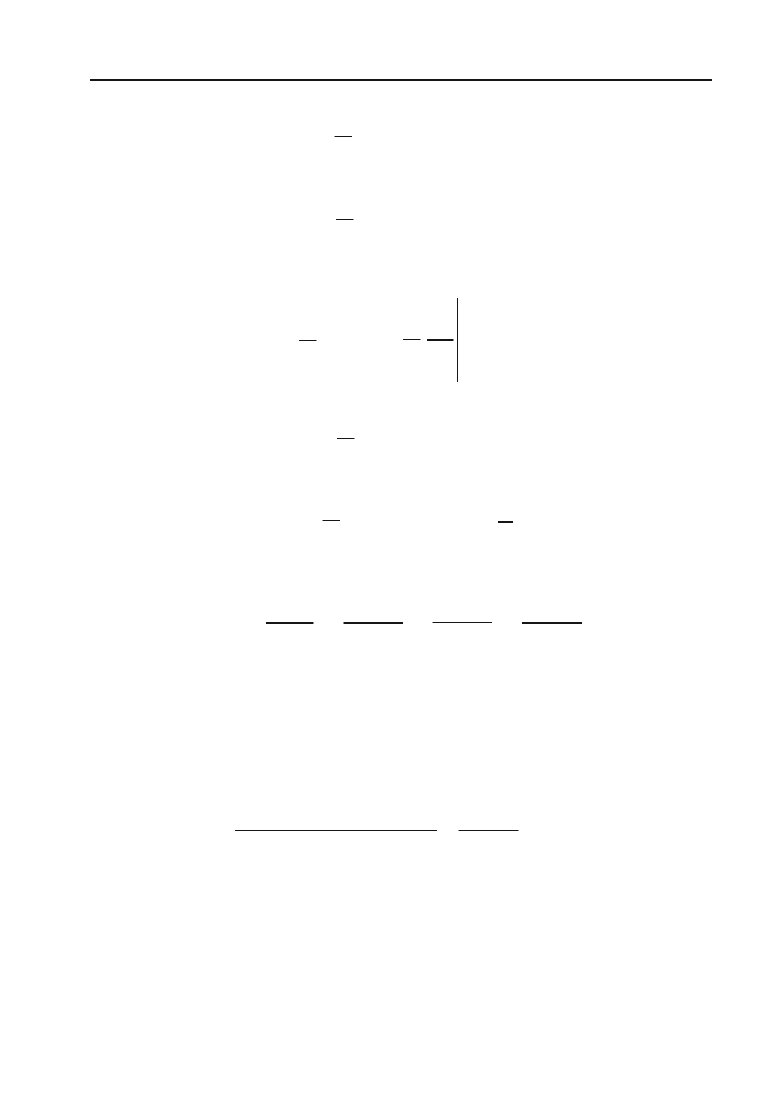
545
Розділ VIII. Ряди
а
n
=
2
0
1
()cos
f
xnxdx
S
S
³
;
b
n
=
2
0
1
()sin
f
xnxdx
S
S
³
.
В нашому випадку маємо:
а
0
=
2
0
1
xdx
S
S
³
=
1
S
2
2
0
2
x
S
=
2
S
;
а
n
=
2
0
1
cos
x
nxdx
S
S
³
= 0;
b
n
=
2
0
1
sinxnxdx
S
S
³
=
2
n
.
Підставляючи одержані значення в формулу (8.36), одержуємо:
x =
S
– 2(
sin
1
x
+
sin 2
2
x
+
sin3
3
x
+
sin 4
4
x
+ …).
Так як на інтервалі (0;
2
S
) функція f(x) = x неперервна, то одер+
жаний ряд збігається до
х у всіх точках цього інтервалу. В точках х
=
2 n
S
(n = 0, 1, 2, …), які являються точками розриву функції ряд
збігається до середнього арифметичного ліво+ та правосторонніх гра+
ниць функції, тобто до числа
(2 0) (2 0) 2 0
22
ff
SSS
=
S
.
Отже, в точках розриву сума ряду дорівнює
S
.

546
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
8.7.4. Розв’язання прикладів
Приклад 8.46. Функцію f(x) =
4
S
–
2
x
розкласти в ряд коси+
нусів на інтервалі (0;
S
).
8.7.3. Розклад в ряд Фур’є функцій, що задані на півперіоді
Функцію, що задана на півперіоді (0;
S
) можна розкласти (по
бажанню) в ряд синусів або в ряд косинусів, продовжуючи на дру+
гий півперіод (–
S
; 0) відповідно непарним або парним чином.
а) Якщо потрібно розкласти таку функцію в ряд по косинусам,
то із інтервалу (0;
S
) в сусідній інтервал (–
S
; 0) необхідно зробити
парне продовження функції, а потім поза інтервалом (–
S
;
S
) вико+
нати її періодичне продовження з періодом
2
S
.
Ряд буде мати вигляд
f(x) =
0
2
a
+
1
cos
n
n
anx
f
¦
,
а коефіцієнти визначаються за формулою:
a
n
=
2
S
0
()cos
f
xnxdx
S
³
.
б) Якщо ж потрібно функцію
f(x), що задано в інтервалі (0;
S
)
розкласти в ряд по синусам, то в сусідній інтервал (–
S
; 0) потрібно
зробити її непарне продовження, а потім періодично продовжити її з
періодом
2
S
.
В цьому випадку ряд буде мати вигляд:
f(x) =
1
sin
n
n
bnx
f
¦
;
а коефіцієнти
b
n
визначаються за формулою:
b
n
=
2
S
0
()sinfx nxdx
S
³
.
547
Розділ VIII. Ряди
Розв’язок. Продовжуючи цю функцію парним чином, як показано
на рис. 8.3 — пунктиром, будемо мати:
а
0
=
2
S
0
()
42
x
dx
S
S
³
=
2
S
(
4
S
х –
2
2
x
)
0
S
=
2
S
(
2
4
S
–
2
4
S
) = 0.
а
n
=
2
S
0
()cos
42
x
nxdx
S
S
³
=
1
,
42 2
1
cos , cos sin
ududx
dv nxdx v nxdx nx
n
SS
³
=
=
2
S
((
4
S
–
2
x
)
sin nx
n
0
S
–
0
1sin
2
nx
dx
n
S
³
) =
1
n
S
0
sinnxdx
S
³
=
= –
2
0
cosnx
n
S
S
= –
2
cos n
n
S
S
+
2
1
n
S
=
2
1
n
S
– (–1)
n
2
1
n
S
=
2
1
n
S
(1 – (– 1)
n
);
a
2k
= 0; a
2k+1
=
2
2
(2 1)k
S
.
Отже,
Y
4
S
4
S
S
2
S
0
2
S
S
X
Рис. 8.3.
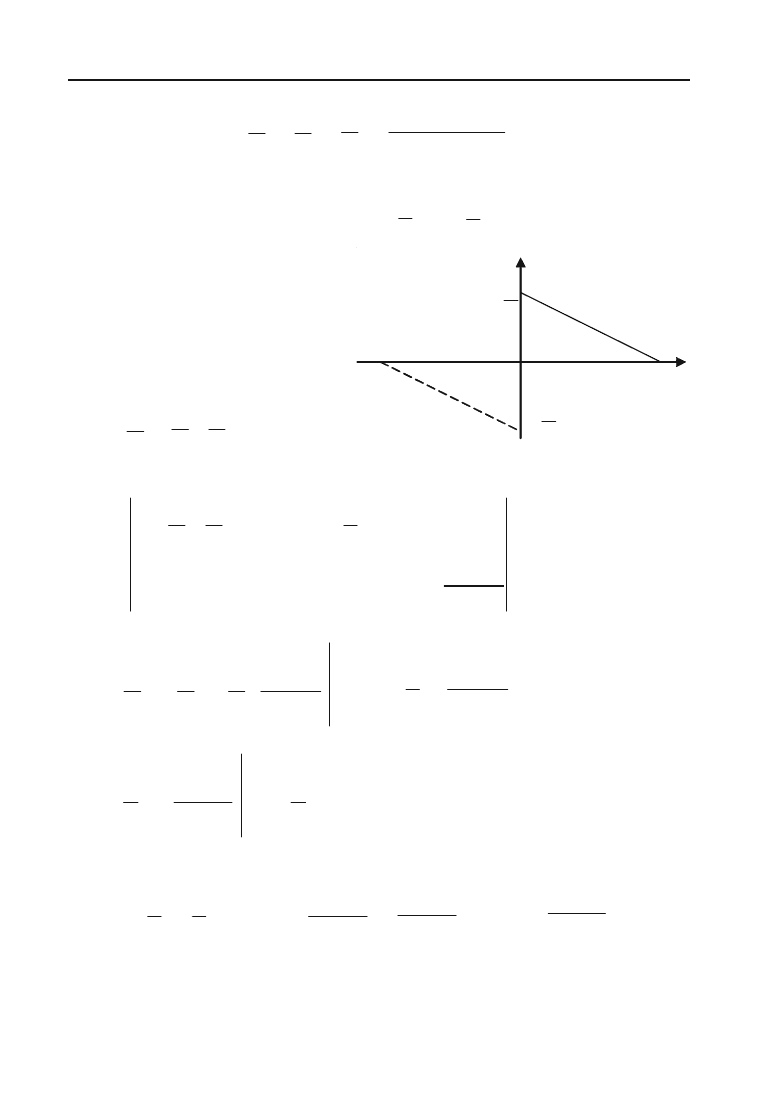
548
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4
S
–
2
x
=
2
0
2cos(21)
(2 1)
k
kx
k
S
f
¦
.
Приклад 8.47. Функцію f(x) =
1
2
S
–
1
2
x
розкласти в ряд си+
нусів на інтервалі (0;
S
).
Розв’язок. Продовжуючи
цю функцію непарним чином,
як показано на рис. 8.4. пунк+
тиром, будемо мати:
b
n
=
2
S
0
()sin
22
x
nxdx
S
S
³
=
=
1
,
22 2
cos
sin , sin
x
ududx
nx
dv nxdx v nxdx
n
S
³
=
=
2
S
(–(
2
S
–
2
x
)
cos
nx
n
0
S
–
0
1cos
())
2
nx
dx
n
S
³
=
=
1
n
–
2
sin
nx
n
S
0
S
=
1
n
.
Отже,
1
2
–
1
2
x = sin x +
sin 2
2
x
+
sin3
3
x
+ … =
1
sin
n
nx
n
f
¦ .
Рис. 8.4.
Y
4
S
4
S
S
0
S
X
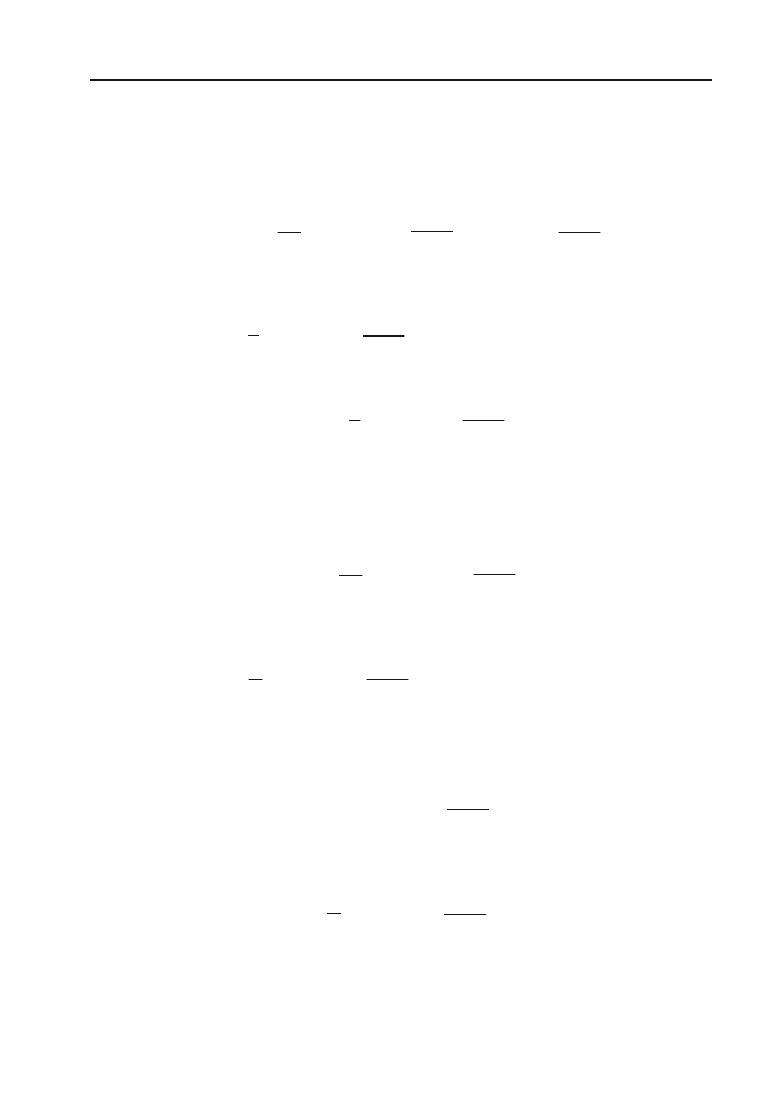
549
Розділ VIII. Ряди
8.7.5. Розклад в ряд Фур’є функції з періодом 2l
Якщо період функції f(x) дорівнює не
2
S
, а 2l, то її ряд Фур’є
має вигляд:
f(x) =
0
2
a
+
1
cos
n
n
nx
a
l
S
f
¦
+
1
sin
n
n
nx
b
l
S
f
¦
, (8.39)
а коефіцієнти цього ряду
а
0
, а
n
, b
n
обчислюються за формулами:
а
n
=
1
l
()cos
l
l
nx
fx dx
l
S
³
, (n = 0, 1, 2, 3, …);
b
n
=
1
l
()sin
l
l
nx
fx dx
l
S
³
. (8.40)
Якщо функція
f(x) на інтервалі (–l; l) парна, то всі коефіцієнти
b
n
= 0, її розклад в ряд Фур’є містить тільки сталу і косинуси і має
вигляд:
f(x) =
0
2
a
+
1
cos
n
n
nx
a
l
S
f
¦
.
Коефіцієнти розкладу а
n
дорівнюють в цьому випадку:
а
n
=
2
l
()cos
l
l
nx
fx dx
l
S
³
, (n = 0, 1, 2, 3, …).
Якщо ж на інтервалі (–
l; l) функція f(x) — непарна, то а
0
= а
n
= 0,
її ряд Фур’є містить тільки синуси та має вигляд:
f(x) =
1
sin
n
n
nx
b
l
S
f
¦
,
а коефіцієнти
b
n
=
2
l
()sin
l
l
nx
fx dx
l
S
³
.
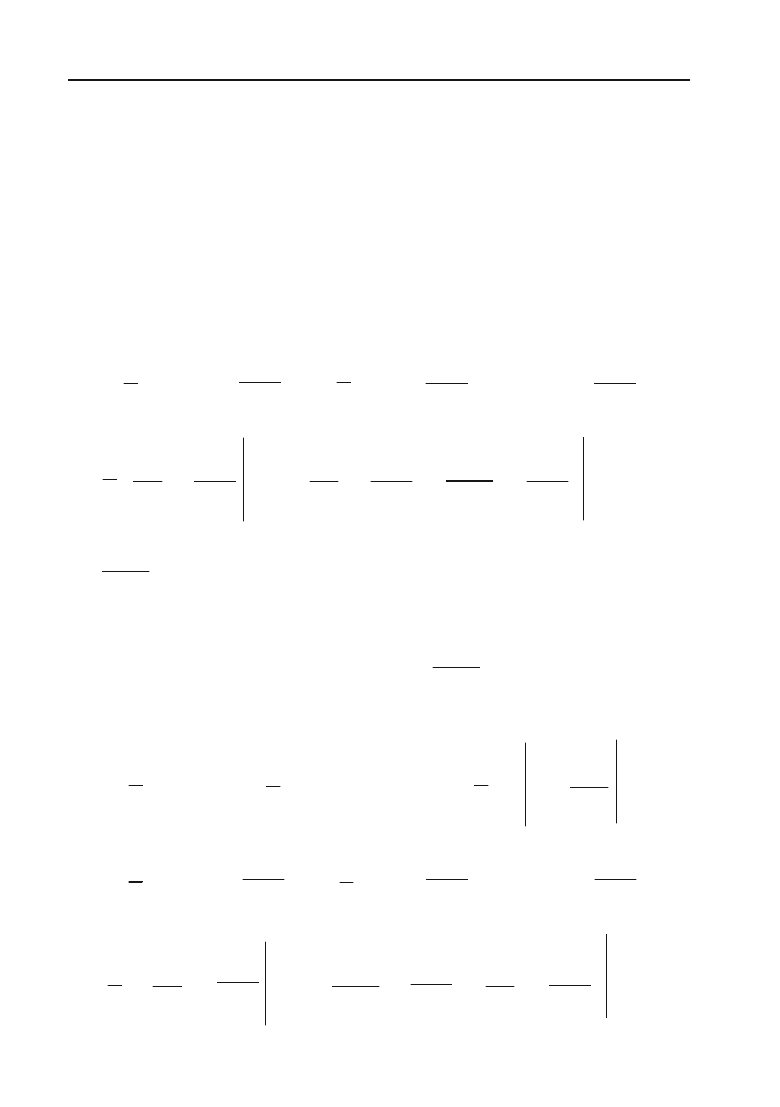
550
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
8.7.6. Розв’язання прикладів
Приклад 8.48. Розкласти в ряд Фур’є функцію
6, 0 2,
()
3 , 2 4.
якщо x
fx
xякщо x
®
¯
Розв’язок. Користуючись формулами (8.40), маючи l = 2 та роз+
биваючи інтервал інтегрування (0; 4) точкою
х = 2 на дві частини,
так як в кожній із них функцію задано різними формулами, одер+
жуємо:
a
n
=
1
2
4
0
()cos
2
nx
fx dx
S
³
=
1
2
(
2
0
6cos
2
nx
dx
S
³
+
4
2
3cos
2
nx
xdx
S
³
) =
=
1
2
(
12
n
S
sin
2
nx
S
2
0
+ 3(
2
x
n
S
sin
2
nx
S
+
22
4
n
S
cos
2
nx
S
)
4
2
) =
=
22
6
n
S
(1– cos pn), n
z
0.
Якщо n парне: cos pn = 1 і a
n
= 0;
Якщо
n непарне: cos pn = –1 і a
n
=
22
12
n
S
;
Якщо
n = 0 за формулою (8.40) одержуємо:
a
0
=
1
2
4
0
()
f
xdx
³
=
1
2
(
2
0
6
dx
³
+
4
2
3
xdx
³
) =
1
2
(6x
2
0
+
2
3
2
x
4
2
) = 15.
b
n
=
1
2
4
0
()sin
2
nx
fx dx
S
³
=
1
2
(
2
0
6sin
2
nx
dx
S
³
+
4
2
3sin
2
nx
xdx
S
³
) =
=
1
2
(
12
n
S
cos
2
nx
S
2
0
+ 3(
22
4
n
S
sin
2
nx
S
–
2
x
n
S
cos
2
nx
S
)
4
2
) =
