Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

531
Розділ VIII. Ряди
Дослідимо збіжність одержаного ряду за ознакою Даламбера:
U
n
=
(2)
2
n
n
x
; U
n+1
=
1
1
(2)
2
n
n
x
.
l =
lim
n
of
1
n
n
U
U
=
|2|
2
x
; l < 1, якщо
|2|
2
x
< 1.
Розв’язавши цю нерівність |x + 2| < 2, знаходимо інтервал –4 < x < 0.
Дослідимо границі цього інтервалу. Підставляючи в ряд
х = –4, а потім
х = 0, одержуємо числові ряди 1 – 1 + 1 – 1 + ... і 1 + 1 + 1 + 1 + ...,
які розходяться, так як у них не виконується необхідної умови
збіжності ряду. Отже, інтервал збіжності одержаного ряду Тейлора
для заданої функції є (–4;
0). Досліджуючи залишковий член R
n
формули Тейлора для заданої функції, переконаємося, що в указа+
ному інтервалі одержаний ряд збігається до заданої функції.
Приклад 8.27. Розкласти в ряд функцію f(x) =
2
2
1
x
e
x
.
Розв’язок.
Так як за (8.28)
е
х
= 1 + х +
2
2!
x
+
3
3!
x
+ ... +
!
n
x
n
+ ...,
то замінивши
х на –х
2
одержуємо:
2
x
e
= 1 – х
2
+
4
2!
x
–
6
3!
x
+ ... + (–1)
n
2
!
n
x
n
+ ...
1 –
2
x
e
= х
2
–
4
2!
x
+
6
3!
x
+ ... + (–1)
n+1
2
!
n
x
n
+ ...
і нарешті,
2
2
1
x
e
x
= 1 –
2
2!
x
+
4
3!
x
– ... + (–1)
т+1
22
!
n
x
n
+ ...
Область збіжності ряду (
;f f
).
Приклад 8.28. Розкласти в ряд функцію f(x) = ln
1
1
x
x
.
532
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок. В розкладі
ln(1 +
x) = x –
2
2
x
+
3
3
x
– ... + (–1)
n+1
n
x
n
+ ...,
замінимо х на –х. Одержимо
ln(1 –
x) = – х –
2
2
x
–
3
3
x
– ... –
n
x
n
– ...
Тепер
ln
1
1
x
x
= ln(1 + x) – ln(1 – x) = (x –
2
2
x
+
3
3
x
– ... + (–1)
n+1
n
x
n
+ ...) –
– (
–х –
2
2
x
–
3
3
x
– ... –
n
x
n
– ...) = 2(x +
3
3
x
+
5
5
x
+ ... +
21
21
n
x
n
+ ...)
Область збіжності ряду (–1; 2).
Приклад 8.29. Розкласти в ряд Маклорена функцію f(x) = cos
2
x.
Розв’язок. Відомо, що cos
2
x =
1
2
(1 + cos 2x). Розклад функції
cos 2
x в ряд Маклорена легко можна отримати, замінивши в фор+
мулі (8.30)
х на 2х:
cos 2
x = 1 –
2
(2 )
2!
x
+
4
(2 )
4!
x
–
6
(2 )
6!
x
+ ... + (–1)
n
2
(2 )
(2 )!
n
x
n
+ ...
Одержуємо, що
cos
2
x =
1
2
(1 + (1 –
2
(2 )
2!
x
+
4
(2 )
4!
x
–
6
(2 )
6!
x
+ ... + (–1)
n
2
(
2
)
(
2
)
!
n
x
n
+ ...)),
звідки:
cos
2
x = 1 –
2
2
2!
x
+
34
2
4!
x
–
56
2
6!
x
+ (–1)
n
212
2
(2 )!
nn
x
n
+ ...
Область збіжності одержаного ряду (
;f f
).
533
Розділ VIII. Ряди
8.5.4. Приклади для самостійного розв’язку
В прикладах 8.30 – 8.36 розкласти задані функції по степенях х
користуючись формулами розкладу в ряд Маклорена функцій е
х
,
sin
x, cos x, ln(1 + x), (1 + x)
m
.
7.30. f(x) =
1
x
e
x
. 7.31. f(x) = sin
2
x
.
7.32. f(x) = sin
2
x. 7.33. f(x) = x ln(1 + x
2
).
7.34. f(x) = ln
3
12
1
x
x
. 7.35. f(x) =
2
1 x
.
7.36. f(x) =
3
3
8 x
.

534
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§8.6. Застосування рядів до наближених обчислень
Степеневі ряди мають самі різні застосування. З їх допомогою
обчислюють з заданою степеню точності значення функції, визначені
інтеграли, які не виражаються через елементарні функції або є за+
надто складними для обчислень, інтегруються диференційні рівнян+
ня. Для обчислення наближених значень функції з заданою точні+
стю зручно користуватися рядами в тому випадку, якщо відповідний
ряд є знакопереміжним. Для знакопереміжного збіжного ряду легко
оцінити похибку наближеного значення суми — вона не перевищує
абсолютного значення першого із відкинутих членів (ознака Лейбн+
іца). В інших випадках наближене значення функції з заданою точ+
ністю обчислюється за формулою Тейлора (Маклорена).
8.6.1. Розв’язання прикладів
Приклад 8.37. Обчислити
4
1
e
з точністю до 0,001.
Розв’язок. Використаємо ряд
е
х
= 1 + х +
2
2!
x
+
3
3!
x
+ ... +
!
n
x
n
+ ...
4
1
e
=
1
4
e
.
Отже, в цьому ряду необхідно взяти
х =
1
4
. Одержимо знакопере+
міжний ряд:
1
4
e
= 1 –
1
4
+
2
11
2! 4
§·
¨¸
©¹
+ ... + (–1)
n–1
1
(1)!n
1
1
4
n
§·
¨¸
©¹
+ ... =
= 1 –
1
4
+
1
32
–
1
384
+ ... + (–1)
n–1
1
(1)!n
1
1
4
n
§·
¨¸
©¹
+ ...
Якщо для обчислення взяти
n перших членів, то, враховуючи,
що ряд знакопереміжний, похибка від відкидання решти членів бу+
де менше абсолютної величини першого відкинутого члена, тобто
535
Розділ VIII. Ряди
R
n
<
1
!n
1
4
n
§·
¨¸
©¹
. За умовою повинно бути одержане число з точністю
до 0,001, тобто загальна похибка від відкидання членів і від округ+
лення повинна бути менше 0,0005. якщо зберегти перші чотири чле+
на, то похибка від відкидання всіх останніх членів на основі ознаки
Лейбніца
R
4
<
1
4!
4
1
4
§·
¨¸
©¹
< 0,00016, через це:
4
1
e
|
1 –
1
4
+
2
11
2! 4
§·
¨¸
©¹
–
3
11
3! 4
§·
¨¸
©¹
|
0,799.
Обчислити з округленням треба тільки останній додаток. Якщо
зберегти чотири десятичні знаки, то похибка округляється не більше
0,00005. Найвища межа загальної похибки дорівнює 0,00021. Отже,
4
1
e
|
0,799.
Приклад 8.38. Знайти наближене значення соs 10° з точністю до
0,0001.
Розв’язок. Переведемо градусну міру в радіанну 10°=
18
S
|
0,1745.
Скористуємося розкладом cos
х в степеневий ряд
cos
x = 1 –
2
2!
x
+
4
4!
x
–
6
6!
x
+ ... + (–1)
n–1
22
(2 2)!
n
x
n
+ ...
Одержуємо
cos 10°
= cos
18
S
= 1 –
2
18
2!
S
§·
¨¸
©¹
+
4
18
4!
S
§·
¨¸
©¹
– ...
цей ряд є рядом Лейбніца, через це, прийнявши за наближене зна+
чення cos 10° суму перших двох членів розкладу, виконаємо похиб+
ку
R
3
за абсолютною величиною меншу третього члена
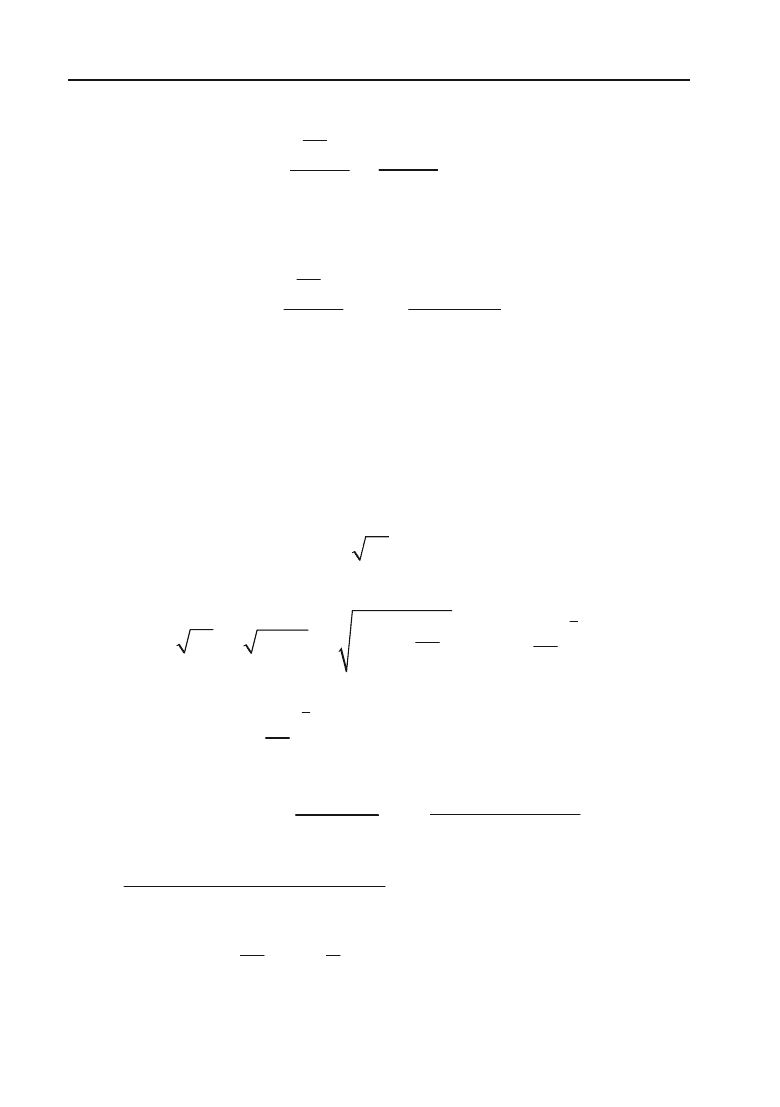
536
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
|R
3
| <
4
18
4!
S
§·
¨¸
©¹
<
4
(0,2)
24
< 0,0001.
Таким чином,
cos 10°
|
1 –
2
18
2!
S
§·
¨¸
©¹
|
1 –
2
(0,1745)
24
|
0,9948.
З точністю до 0,0001, з недостачею, так як третій член розкладу
додатний. Обчислюючи суму перших двох членів з точністю до 10
+4
з залишком (для того, щоб обчислити другий член з тією ж точністю
з недостачею), одержимо абсолютну похибку, тобто повну похибку,
меншу 0,0001, відповідно з завданням (таке як обидві похибки були
менше 10
+4
і мають різні знаки). Отже, cos 10°
|
0,9948.
Приклад 8.39. Обчислити
4
17
з точністю до 0,001.
Розв’язок. Перетворимо заданий корінь
4
17
=
4
16 1
=
4
1
16 1
16
§·
¨¸
©¹
=
1
4
1
21
16
§·
¨¸
©¹
.
Для обчислення
1
4
1
1
16
§·
¨¸
©¹
використаємо біноміальний ряд
(1 +
x)
m
= 1 + mx +
(1)
2!
mm
x
2
+
(1)(2)
3!
mm m
x
3
+ ... +
+
( 1)( 2)...( 1)
!
mm m m n
n
x
n
+ ...,
підставляючи
х =
1
16
, m =
1
4
:

537
Розділ VIII. Ряди
1
4
1
21
16
§·
¨¸
©¹
= 2(1 +
1
416
–
2
13
4816
+
3
137
481216
– ...).
Щоб визначити, скільки необхідно взяти перших членів цього
знакопереміжного ряду для обчислення
4
17
з точністю до 0,0001,
обчислимо декілька послідовних перших членів ряду:
а
1
= 1; а
2
|
0,01562; а
3
|
–0,00037; а
4
|
0,00001. Згідно властивості знакоперем+
іжного збіжного ряду, якщо обмежитися сумою трьох перших членів
ряду, то похибка шуканого наближеного значення кореня буде мен+
шою 2
а
4
|
20,00001 < 0,0001. Отже,
4
17
|
2(1 + 0,1562 – 0,00037)
|
2,0305.
Приклад 8.40. Обчислити інтеграл
1/4
0
sin x
dx
x
³
з точністю до
0,00001.
Розв’язок. Невизначений інтеграл
sin x
dx
x
³
не виражається че+
рез елементарні функції, через це при обчисленні даного визначено+
го інтегралу формулу Ньютона+Лейбніца застосовувати не можна.
Обчислимо інтеграл наближено. Розділивши почленно ряд
sin
x = х –
3
3!
x
+
5
5!
x
–
7
7!
x
+ ...
на х, одержимо:
sin x
x
= 1 –
2
3!
x
+
4
5!
x
–
6
7!
x
+ ...
Інтегруємо цей ряд почленно:
1/4
0
sin x
dx
x
³
=
1/4
246
0
1...
3! 5! 7!
xxx
dx
§·
¨¸
©¹
³
=
1
4
–
1
33!
3
1
4
§·
¨¸
©¹
+
+
1
55!
5
1
4
§·
¨¸
©¹
– ...
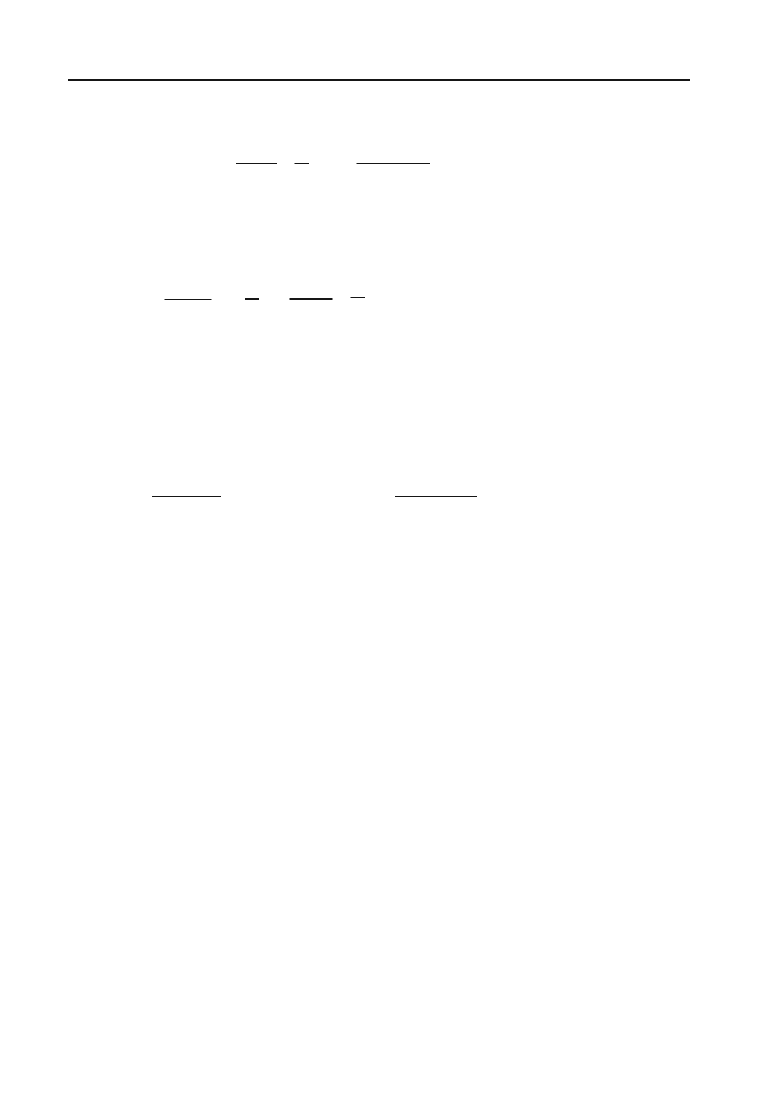
538
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Так як
1
55!
5
1
4
§·
¨¸
©¹
=
1
614400
< 0,00001,
то за ознакою Лейбніця, щоб виконати задану точність, досить взяти
суму перших двох членів:
1/4
0
sin x
x
³
|
1
4
–
1
33!
3
1
4
§·
¨¸
©¹
= 0,25 – 0,00087 = 0,24913.
8.6.2. Приклади для самостійного розв’язку
7.41. Обчислити визначені інтеграли з точністю до 0,001.
а)
1/2
0
arctg x
dx
x
³
;б)
1/10
0
ln(1 )x
dx
x
³
;
в)
1
2
0
sin xdx
³
;г)
2
1/4
0
x
edx
³
.
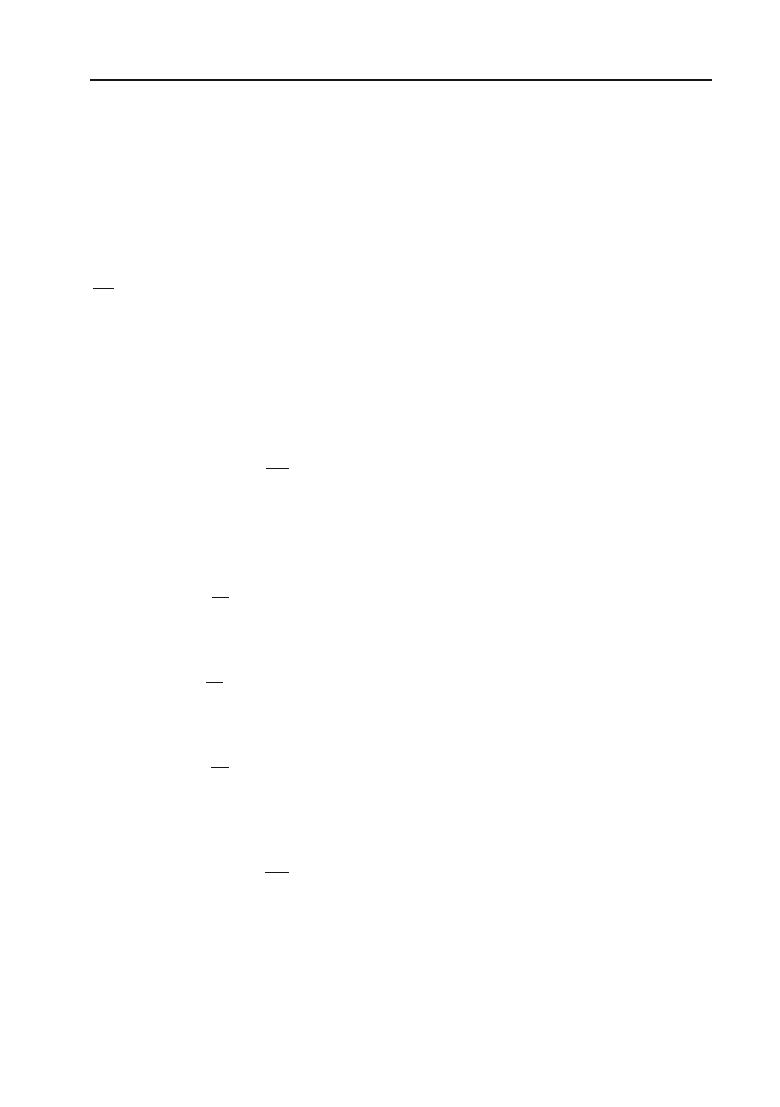
539
Розділ VIII. Ряди
§8.7. Ряди Фур’є
8.7.1. Розклад в ряди Фур’є функції з періодом
2
S
Нехай f(x) — функція з періодом
2
S
, що інтегрується на
[
;
]
SS
.
Ряд виду:
0
11 2 2 3 3
(
cos sin
)(
cos2 sin 2
)(
cos3 sin 3
)
2
a
axbxa xb xa xb x
+
(
cos sin
)
nn
anxbnx + ... (8.34)
називається
тригонометричним рядом функції f(x). Числа а
1
, а
2
, ... ,
а
n
, ..., b
1
, b
2
, b
3
, … , b
n
, … називаються коефіцієнтами тригонометрич,
ного ряду
. Цей ряд в скороченому вигляді може бути записаний так:
0
1
( cos sin )
2
nn
n
a
anxbnx
f
¦
. (8.34)
Тригонометричний ряд називається також
рядом Фур’є, коефіці+
єнти якого визначаються за формулами:
а
0
=
1
()fxdx
S
S
S
³
;
а
n
=
1
()cosfx nxdx
S
S
S
³
(n = 1, 2, 3, ...); (8.35)
b
n
=
1
()sin
f
xnxdx
S
S
S
³
(n = 1, 2, 3, ...).
При цьому пишуть так:
f(x)
|
0
1
( cos sin )
2
nn
n
a
anxbnx
f
¦
. (8.36)
Ряд Фур’є функції
f(x) не завжди своєю сумою має f(x), якщо
навіть збігається. Найпростішими достатніми ознаками розкладу
функції в ряд Фур’є є:
540
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1. Якщо функція f(x) з періодом
2
S
має на відрізку
[;]
SS
скінчене число точок розриву першого роду і абсолютно інтегрована
на цьому відрізку, то ця функція розкладається в свій ряд Фур’є в
кожній точці, в якій вона диференційовна.
2. Якщо функція з періодом
2
S
задовольняє умовам Дірихле на
відрізку
[;]
SS
(якщо цей відрізок може бути розбитий на скінчене
число частин так, що всередині кожної частини функція монотонна
і обмежена), то ця функція розкладається в свій ряд Фур’є в кожній
точці неперервності, якщо ж
х — точка розриву, ряд Фур’є збігається
до числа:
(0)(0)
2
fx fx
.
Ряд Фур’є парної функції, тобто
f(x) = f(–x), не містить членів з
синусами; цей ряд має вигляд:
f(x)
|
0
1
cos
2
n
n
a
anx
f
¦
, (8.37)
де
а
0
=
0
2
()fxdx
S
S
³
;
а
n
=
0
2
()cosfx nxdx
S
S
³
, (n = 1, 2, 3, ...).
Ряд Фур’є непарної функції, тобто
f(–x)= –f(x), не містить
вільного члена і членів з косинусами; цей ряд має вигляд:
f(x)
|
1
sin
n
n
bnx
f
¦
, (8.38)
де
b
n
=
0
2
()sinfx nxdx
S
S
³
, (n = 1, 2, 3, ...).
