King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

We general ize the Lagrange method for any interpolating polynomial of degree n.

The kth Lagrange polynomial of order n is given by

ðxÞ¼

x  x

ðÞx  x

ð Þ x  x

k1

ðÞx  x

kþ1

ð Þ x  x

ðÞ

 x

ðÞx

 x

ð Þ x

 x

k1

ðÞx

 x

kþ1

ðÞx

 x

ðÞ

: (6:15)

Note that L

ðxÞ does not contain the term x  x

ðÞin the numerator. When x ¼ x

the numerator of L

equals the denominator and L

¼ 1. For which values of x does

¼ 0?

Lagrange interpolation for generating an nth-degree polynomial involves the

construction of n + 1 Lagrange polynomials. To evaluate pðxÞone needs to calculate

the values of the n +1nth-order Lagrange polynomials. The Lagrange interpolation

formula for the nth-degree polynomial pðxÞ is

pxðÞ¼

k¼0

∏

j¼0; j6¼k

x  x



 x



k¼0

: (6:16)

A drawback of the Lagrange method is that to interpolate at a new value of x it is

necessary to recalculate all individual terms in the expansion for pxðÞ. Manual

calculation of the Lagrange polynomials is cumbersome for interpolating polyno-

mials of degree ≥ 3.

If the function fxðÞthat deﬁnes the data is differentiable n + 1 tim es in the interval

[a, b ], which contains the n + 1 points at which the function values are known, the

error in polynomial inter polation is given by Equation (6.17):

ExðÞ¼

nþ1

ξðxÞðÞ

n þ 1ðÞ!

x  x

ðÞx  x

ð Þ x  x

ðÞa  ξ  b: (6:17)

The location of ξ is a function of x. Note that this term is similar to the error term of

the Taylor series. The error depends on (1) the location of the x value within the

interval [a, b], (2) the degree of the interpolating polynomial, (3) the behavior of the

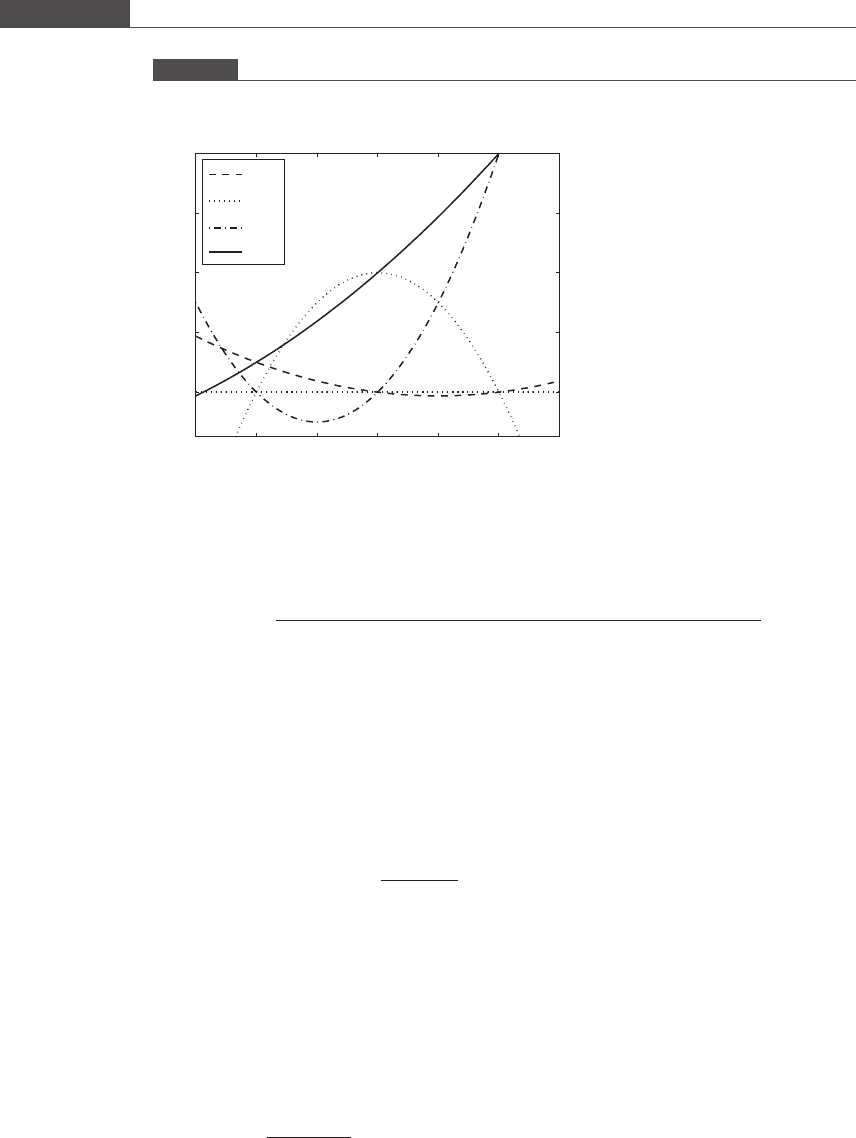
Figure 6.6

The 2nd-degree interpolating polynomial is the sum of three quadratic Lagrange functions. The polynomial interpolates

between three points (1, 1), (2, 4), and (3, 8).

0.5 1 1.5 2 2.5 3 3.5

p(x)

367

6.2 Polynomial interpolation

actual function, and (4) the location of the n + 1 nodes. The derivation of Equation

(6.17) requires the use of advanced calculus concepts (e.g. generalized Rolle’s

theorem) which are beyond the scope of this book. The interested reader is referred

to Burden and Faires (2005) for the proof. Because the error cannot be evaluated, it

is not possible to deduce the degree of the polynomial that will give the least error

during interpolation. Increasing the degree of the interpolating polynomial does not

necessarily improve the quality of the approximation.

Box 6.2 Transport of nutrients to cells suspended in cell culture media

Suspended spherical cells placed in a nutrient medium may survive (and multiply) for a period of time if

critical solutes/nutrients are available. If the cell media is kept stationary (not swirled or mixed – no

convective currents

), the nutrients in the media spread by diffusing through the liquid medium to the

cell surface, where they either diffuse through the cell membrane or react with cell membrane proteins

(includes receptors and channels). If uptake of a solute is rapid, the concentration of the solute at the

cell surface is negligible, and the process by which the cells acquire the desired nutrient is said to be

“transport-limited” or “diffusion-limited.” In a spherical coordinate system, solute transport towards a

spherical cell of radius a is governed by the following mass balance equation:

∂C

¼ D

∂

∂r

∂C

∂r



;

where D

is the binary diffusion coefficient of diffusing species i in water. The mixture is assumed to be

dilute. We are only interested in the transport of species A.

The initial and boundary conditions for this system are

r; tðÞ¼C

; for r  a; t ¼ 0;

r; tðÞ¼0; for r ¼ a; t

r; tðÞ¼C

; for r ! ∞; t

Figure 6.7 illustrates the system geometry.

Figure 6.7

Diffusion of solute through the medium to the cell surface.

Cell

Cell culture medium

Concentration far from cell: C

= C

Solute diffusivity: D

A, surface

= 0

While the cells will settle on the bottom surface of the ﬂask, we will assume the wall can be neglected in

analyzing the diffusion.

368

Numerical quadrature

The mass balance equation is solved to yield the following analytical solution:

¼ 1 

erfc

r  a

ﬃﬃﬃﬃﬃﬃ

: (6:18)

Equation (6.18) describes the time-varying concentration profile of solute. It contains the comple-

mentary error function, which is defined as

erfc zðÞ¼1  erf zðÞ¼1 

ﬃﬃ

z

dz:

The integral

z

dz cannot be solved analytically. You may recognize this integral as similar in form to

the cumulative normal distribution function discussed in Chapter 3. The error function has the following

property:

ﬃﬃ

∞

z

dz ¼ 1:

The integral solutions for various values of z are available in tabulated form in mathematical handbooks

such as that by Abramowitz and Stegun (1965). The error function values for seven different values of z

are listed in Table 6.1.

The constants in Equation (6.18)areD

=10

−7

/s, a =10μm. Using the values in Table 6.1,we

calculate the solute concentration in the medium at six radial distances from the cell surface at t =10s.

The calculations are presented in Table 6.2.

Table 6.1. Values of error function

z erf(z)

0.0 0.0000000000

0.1 0.1124629160

0.2 0.2227025892

0.5 0.5204998778

1.0 0.8427007929

1.5 0.9661051465

2.0 0.9953222650

Table 6.2. Concentration proﬁle at t = 10 s

r (μm) z erfc(z) C

10 0.0 1.0000000000 0.0000000000

12 0.1 0.8875370830 0.2603857641

14 0.2 0.7772974108 0.4447875637

20 0.5 0.4795001222 0.7602499389

30 1.0 0.1572992071 0.9475669309

40 1.5 0.0338948535 0.9915262866

50 2.0 0.0046777350 0.9990644530

369

6.2 Polynomial interpolation

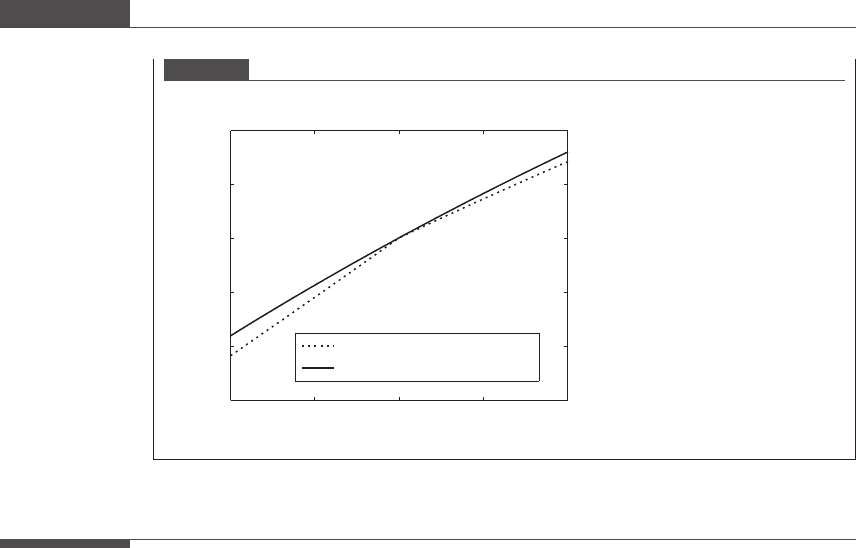
Figure 6.8

Piecewise cubic polynomial interpolant plotted along with the true concentration profile.

10 20 30 40 50

0.2

0.4

0.6

0.8

Radial distance, r (μm)

Piecewise cubic interpolant

True concentration profile

You are asked to use a third-degree piecewise polynomial interpolant to approximate the concen-

tration profile of solution near the cell surface at time t = 10 s. Use the MATLAB polyﬁt function to

obtain the coefficients for the two cubic interpolants.

The first cubic interpolant is created using the first four data points. The MATLAB statements

r = [10 12 14 20];

y = [0.0000000000 0.2603857641 0.4447875637 0.7602499389];

[p S] = polyﬁt(r, y, 3);

give us the following cubic polynomial:

y ¼ 0:000454r

 0:025860r

þ 0 :533675 r  3:205251 for 10  r  20:

The second cubic interpolant is given by

y ¼ 0:000018r

 0:002321r

þ 0 :100910 r  0:472203 for 20  r  50:

The piecewise cubic interpolating function is plotted in Figure 6.8. Using the built-in MATLAB error

function erf, we calculate the true concentration profile (Equation (6.18)). The actual concentration

profile is calculated in a MATLAB script file as follows:

Da = 10; % um^2/s

t=10;%s

a=10;%um

hold on

r = [10:0.1:50];

y=1-a./r.*(1 - erf((r-a)/2/sqrt(Da*t)));

The exact concentration profile is plotted in Figure 6.8 for comparison. The plot shows that there is good

agreement between the cubic polynomial interpolant and the true function.

There is a discontinuity at r =20 μm where the two piecewise interpolants me et. Calculate

the slopes of both functions at r =20 μm and compare them. Fi gure 6.9 shows a magnification

of the region of disc ontinuity. Do your slo pe calculations explain the discontinuous behavior

observed here?

370

Numerical quadrature

6.3 Newton–Cotes formulas

The most widely used numerical quadrature schemes are the Newton–C otes rules.

The Newton–Cotes formulas are obtained by replacing the integrand function with a

polynomial function that interpolates between speciﬁc known values of the inte-

grand. For example, the midpoint rule (which was introduced in Section 6.1)usesa

zero-degree polynomial to represent the integrand function. Because the interpola-

ting function is a constant value within the interval, the function value needs to be

speciﬁed at only one node. The location of the node is at the midpoint of the interval

(and not at the interval endpoints ). Therefore, the midpoint rule is a Newton–

Cotes open integration rule. To improve accuracy of the midpoint method, a piece-

wise constant function can be used to approximate the integrand function.

The entire interval is divided into a number of subintervals and the midpoint rule,

i.e. fxðÞ¼fx

iþ0:5

ðÞfor x 2 x

; x

iþ1

½, is applied to each subinterval. This is called the

composite midpoint rule, which was illustrated in Figure 6.2. The formula for this rule

is given by Equation (6.2). The integration rules that we discuss in this section are

closed integration formulas, i.e. the nodes used to construct the interpolating poly-

nomial (nodes at which the function values are speciﬁed) include both endpoints of

the interval of integration.

A ﬁrst-degree polynomial (n = 1), i.e. a straight line, can be used to interpolate the

two data points that lie at the ends of the interval. Since only two data points are

required to deﬁne a line, and both these points are located at the ends of the interval,

this scheme is a closed form of numerical integration. The straight line approximates

the integrand function over the entire interval. Alternatively, the function can be

represented by a series of straight lines applie d piecewise over the n subintervals.

Numerical integration using linear interpolation or piecewise linear interpolation of

the data generates the trapezoidal rule.

If a second-degree polynomial (n = 2), i.e. a quadratic function, is used to

interpolate three data points, two of which are located at the endpoints of the

interval and a third point that bisects the ﬁrst two, then the resulting integration

rule is called Simpson’s 1/3 rule. For n = 3, a cubic polynomial interpolant (that

Figure 6.9

Discontinuity at r =20μm.

19 19.5 20 20.5 21

0.7

0.72

0.74

0.76

0.78

0.8

Piecewise cubic interpolant

True concentration profile

Radial distance, r (μm)

371

6.3 Newton–Cotes for mulas

connects four data points) of the function is integrate d, and the resulting Newton–

Cotes formula is called Simpson’s 3/8 rule.

A key feature of the Newton–Cotes formulas is that the polynomial function of

degree n must interpolate equally spaced nodes. For example, a second-degree

interpolant is constructed using function values at three nodes. Since two of the

nodes are the interval endpoints, the integration interval is divided into two parts by

the third node, located in the interior of the interval. The subinterval widths must be

equal. In other words, if the node points are x

; x

; and x

, and x

, then

 x

¼ x

 x

¼ h. In general, the n + 1 nodal points within the closed interval

½a; b must be equally spaced.

6.3.1 Trapezoidal rule

The trapezoidal rule is a Newton–Cotes quadrature method that uses a straight line

to approximate the integrand function. The straight line is constructed using the

function values at the two endpoints of the integration interval. The Lagrange

formula for a ﬁrst-degree polynomial interpolant given by Equation (6.12) is repro-

duced below:

pxðÞ¼

x  x

ðÞ

 x

ðÞþ

x  x

ðÞ

 x

ðÞ:

The function values at the integration limits, a ¼ x

and b ¼ x

, are used to derive

the straight-li ne polynomial. The equation above c ontains two ﬁrst-order

Lagrange polynomials, which upon integration produce the weights of the numer-

ical integration formula of Equation (6.1).Leth ¼ x

 x

. The integral of the

function fðxÞ is exactly equal to the integral of the corresponding ﬁrst-degree

polynomial interpolant plus the integral of the truncation error associated with

interpolation, i.e.

fxðÞdx ¼

x  x

ðÞ

 x

ðÞþ

x  x

ðÞ

 x

ðÞ



ξðxÞðÞ

x  x

ðÞx  x

ðÞdx; a  ξ  b:

Performing integration of the interpolant, we obtain

fxðÞdx 

x  x

ðÞ

 x

ðÞþ

x  x

ðÞ

 x

ðÞ



fx

ðÞ

x  x

ðÞdx þ fx

ðÞ

x  x

ðÞdx



fx

ðÞ

 x

ðÞ



þ fx

ðÞ

 x

ðÞ



;

fxðÞdx 

ðÞþfx

ðÞðÞ:

(6:19)

Equation (6.19) is called the trapezoidal rule. It is the formula used to calculate the

area of a trapezoid. Thus, the area under the straight-line polynomial is a trapez oid.

Figure 6.10 presents the graphical interpretation of Equation (6.19).

372

Numerical quadrature

Now we calculate the error associated with using a linear interpolant to approxi-

mate the function fðxÞ. We assume that the function is twice differentiable on the

interval range. For some value ξ in the interval, we have

E ¼

ξðÞ

x  x

ðÞx  x

ðÞdx:

The integral is evaluated as

x  x

ðÞx  x

ðÞdx ¼



þ x



þ x



 x



þ 3x

 x

ðÞ



 x

ðÞ

¼

Thus, the error term becomes

E ¼

ξðÞ: (6:20)

The error of the trapezoidal rule is exactly zero for any function whose second

derivative is equal to zero.

The accuracy or precision of a quadrature rule is defined as the largest positive integer n such that

the rule integrates all polynomials of degree n and less with an error of zero.

The second derivative of any linear function is zero.

The degree of precision of the trapezoidal rule is one. The error of the trapezoidal rule is Oh



Equation (6.19) is the trapezoidal rule applied over a single interval. If the interval of

integration is large, a linear function may be a poor choice as an approximating

Figure 6.10

The trapezoidal rule for numerical integration. The shaded area is a trapezoid.

y = f(x)

= p(x)

, f(x

))

, f (x

))

We can take f

ξðÞout of the interval because x  x

ðÞx x

ðÞdoes not change sign over the entire

interval and the weighted mean value theorem applies. While these theorems are beyond the scope of

this book, the interested reader may refer to Burden and Faires (2005), p. 8.

373

6.3 Newton–Cotes for mulas

function over this interval, and this can lead to a large error in the result. To increase

accuracy in the approximation of the integrand function, the interval is divided into

a number of subintervals and the function within each subinterval is approximated

by a straight line. Thus, the actual function fðxÞ is replaced with a piecewise linear

function. The trapezoidal rule for numerical integration given by Equation (6.19) is

applied to each subinterval. The numerical result obtained from each subinterval is

summed up to yield the integral approximation for the entire interval.

If the interval is divided into n subintervals, then the integral can be written as the

sum of n integrals:

fxðÞdx ¼

fxðÞdx þ

fxðÞdx þþ

n1

fxðÞdx:

Now n linear polynomials are constructed from the n + 1 data points, i.e. values of

fxðÞevaluated at x

; x

; ...; x

(whose values are in increasing order). The tra-

pezoidal rule (Equation (6.19)) is applied to each subinterval . The numerical approx-

imation of the integral is given by

fxðÞdx 

 x

ðÞ

ðÞþfx

ðÞðÞþ

 x

ðÞ

ðÞþfx

ðÞðÞ

 x

ðÞ

ðÞþfx

ðÞð Þþ

 x

n1

ðÞ

n1

ðÞþfx

ðÞðÞ:

(6:21)

Equation (6.21) is called the composite trapezoidal rule for unequal subinterval widths,i.e.

it applies when the function is not evaluated at a uniform spacing of x. If all subintervals

have the same width equal to h,thenx

¼ x

þ ih,andEquation (6.21) simpliﬁes to

fxðÞdx 

ðÞþ2

n1

i¼1

ðÞþfx

ðÞ

: (6:22)

Equation (6.22) is the composite trapezoidal rule for subintervals of equal width.

Comparing Equation (6.22) with Equation (6.1), you will observe that the composite

trapezoidal rule for numerical integration is the summation of the function values

evaluated at n + 1 points along the interval, multiplied by their respective weights.

Figure 6.11 illustrates the composite trapezoidal rule.

Figure 6.11

The composite trapezoidal rule. The six shaded areas each have the shape of a trapezoid.

, f (x

))

f(x)

374

Numerical quadrature

Next, we calculate the error associated with the composite trapezoidal rule when

the subinterval widths are equal. The integration error of each subinterval is added

to obtain the total error of integration over n subintervals as follows:

E ¼

i¼1

ðÞ¼

ðb  aÞ

12n

i¼1

ðÞ;

where ξ

2 x

i1

; x

½is a point located within the ith subinterval. We deﬁne the

average value of the second deriva tive over the interval of integration:

i¼1

ðÞ:

The quadratur e error becomes

E ¼

ðb  aÞ

12n

¼

ðb  aÞh

; (6:23)

which is Oh



. Note that the error of the composite trapezoidal rule is one

order of magnitude less than the error associated with the basic trapezoid rule

(Equation (6.19)).

Box 6.3A IV drip

A cylindrical bag of radius 10 cm and height 50 cm contains saline solution (0.9% NaCl) that is provided

to a patient as a peripheral intravenous (IV) drip. The method used to infuse saline into the patient’s

bloodstream in this example is gravity drip. The solution flows from the bag downwards under the action

of gravity through a hole of radius 1 mm at the bottom of the bag. If the only resistance offered by the flow

system is the viscous resistance through the tubing, determine the time it will take for the bag to empty

by 90%. The length of the tubing is 36″ (91.44 cm) and its ID (inner diameter) is 1 mm. The viscosity of

the saline solution μ = 0.01 Poise, and the density ρ = 1 g/cm

Let L be the length of the tubing, d the diameter of the tubing, and R the radius of the cylindrical bag.

Then,

L = 91.44 cm; d = 0.1 cm; R = 10 cm.

Mechanical energy balance

The mechanical energy balance is given by the Bernoulli equation corrected for loss of mechanical

energy due to fluid friction. The mechanical energy at the liquid level in the bag is equal to the

mechanical energy of the fluid flowing out of the tubing minus the frictional loss. We ignore the friction

loss from sudden contraction of the cross-sectional area of flow at the tube entrance. The height at which

the drip fluid enters the patient is considered the datum level. The height of the fluid in the bag is z cm

with respect to the bottom of the bag, and is (z + L) cm with respect to the datum level (see

Figure 6.12).

The pressure drop in the tubing due to wall friction is given by the Hagen–Poiseuille equation:

Δp ¼

32Luμ

¼ 2926:08u:

The Bernoulli equation for this system is as follows:

gzþ L

ðÞ

Δp

32Luμ

; (6:24)

375

6.3 Newton–Cotes for mulas

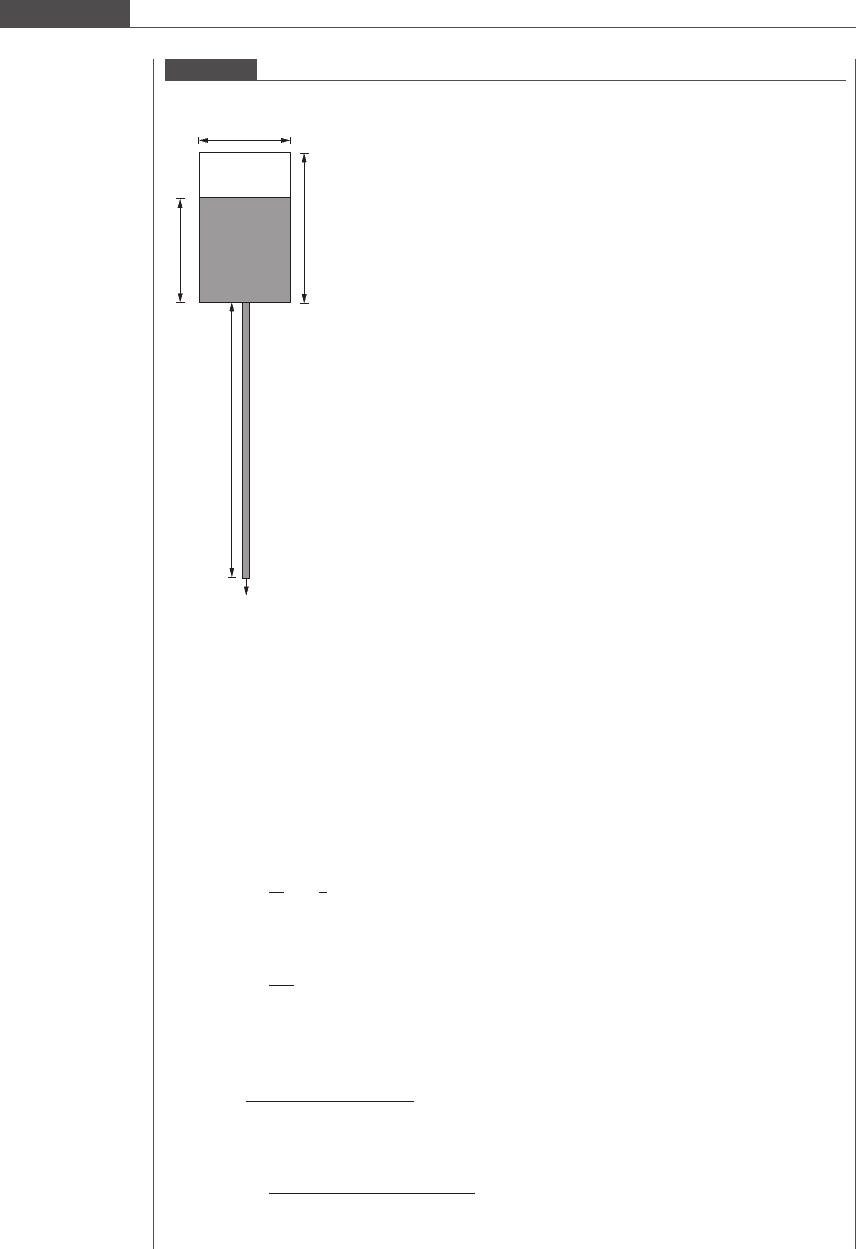
Figure 6.12

Schematic of saline IV drip under gravity.

20 cm

L = 36˝

50 cm

where Δp=ρ is the term for mechanical loss due to fl uid friction and has units of energy per

mass.

Steady state mass balance

There is n o reaction, accumulation, or depl etion wi thin the system, and we ignore the initial unsteady

flow when i nitiating the IV drip. The mass flow rate in the bag is equal to the mass flow rate in the

tubing:

 ρπR

¼ ρ

On rearranging, we get

dt ¼

dz:

We can express u in terms of z by solving Equation (6.24) for u.

Letting α ¼ 64Lμ=d

ρ,

u ¼

α þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ 8gðz þ LÞ

Substituting the above into the steady state mass balance,

dt ¼

α þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ 8gðz þ LÞ



dz:

376

Numerical quadrature