King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

curve. The point of intersection of the quadratic with the x-axis provides the next

estimate of the root. When the secant method or the inverse quadratic interpolation

method produces a diverging solution, the bisection method is employed. Note that,

if the function has a discontinuity, fzero will not be able to distinguish a sign

change at a discontinuity from a zero point and may report the point of discontinuity

as a zero.

The basic syntax for the fzero function is

x = fzero(func, x0)

Here x is the numerically determined root, func is the name of the function whose

zero is required, and x0 can be one of two things: an initial guess value or a bracketing

interval. If x0 is a scalar value, then fzero will automatically search for the nearest

bracketing interval and then proceed to ﬁnd a zero within that interval. If x0 is a

vector containing two values that specify a bracketing interval, the function values

evaluated at the interval endpoints must lie on opposite sides of the x-axis, otherwise

an error will be generated. Note that fzero cannot locate points where the function

touches the x-axis (no change in sign of the function) but does not cross it.

The function whose zero is sought can either be speciﬁed as an m-ﬁle function or

an inline function. Examples of m-ﬁle functions are supplied throughout this chap-

ter. Such functions are deﬁned using the function keyword at the beginning of an

m-ﬁle, and the m-ﬁle is saved with the same name as that of the function. An inline

function is constructed using inline and providing a string expression of the

function as input. For example, entering the following at the command line produces

an inline function object f:

f = inline( ‘ 2*x – 3’)

Inline function:

f(x) = 2*x - 3

f is now a function that can be evaluated at any point x. For example,

f(2)

produces the output

ans =

Let’s use fzero to determine a root of the equation x

 6x

þ 9x  4 ¼ 0

(Equation (5.4)). This equation has three roots, a single root: x = 4 and a double

root at x =1.

We ﬁrst specify only a single value as the initial guess:

fzero(inline(‘x^3 – 6*x^2 + 9*x – 4’),5)

ans =

Now we specify a bracketing interval:

fzero(inline(‘x^3 – 6*x^2 + 9*x – 4’),[3 5])

ans =

4.0000

Let’s try to ﬁnd the double root:

347

5.8 MATLAB function fzero

fzero(inline(‘x^3 – 6*x^2 + 9*x – 4’),0)

ans =

The root x = 1 could not be found.

Let’s specify the interval of search as [0 2] (note that there is no sign change in this

interval):

fzero(inline(‘x^3 – 6*x^2 + 9*x – 4’),[0 2])

??? Error using ==> fzero at 292

The function values at the interval endpoints must differ in sign.

On the other hand, if we specify the interval [−1 1], we obtain

fzero(inline(‘x^3 – 6*x^2 + 9*x – 4’),[-1 1])

ans =

We have found the double root! Since fzero cannot locate double roots, can you

guess how this is possible?

Other ways of calling the fzero function can be studied by typing in the state-

ment help fzero in the Command Window.

5.9 End of Chapter 5: key points to consider

(1) Nonlinear equations of the form f(x) = 0 that are not amenable to analytical

solution can be solved using numerical iterative procedures such as

the bisection method,

the regula-falsi method,

ﬁxed-point iteration,

Newton’s method,

the secant method.

(2) The iterative schemes listed above can be broadly stated in two categories.

(a) Bracketing methods, in which the search for a root of an equ ation is constrained

within a speciﬁed interval that encapsulates a sign change of the function, e.g.

the bisection method and the regula-falsi method.

(b) Open interval methods, in which one or two guesses are speciﬁed initially; how-

ever, the search for the root may proceed in any direction and any distance away

from the initally supplied values, e.g. ﬁxed-point iteration, Newton’s method

and the secant method.

(3) It is critical for the success of these numerical root-ﬁnding methods that f (x) and/or

its derivatives be continuous within the interval of interest in which the root lies.

(4) A comparison of nonlinear root- ﬁnding methods is outlined in Table 5.2.

(5) A generalized Newton’s method can be applied to solve nonlinear multi-equation

systems. The limitations of Newton’s method for solving systems of nonlinear

equations are similar to those faced when solving a nonlinear equation in one

variable.

(6) Hybrid methods of solution combine two or more numerical schemes of root ﬁnding

and are more powerful compared to individual methods of root ﬁnding. A hybrid

method can marshal the strengths of two or more root-ﬁnding techniques to effec-

tively minimize the limitations imposed by any of the individual numerical

techniques.

348

Root-finding techniques for nonlinear equations

(7) The MATLAB-deﬁned function fzero is a hybrid method that uses the bisection

method, secant method, and the inverse quadratic interpolation method to solve for

a zero of a function, i.e. wherever a sign change in the function occurs (excluding

singularities).

5.10 Problems

5.1. Packed bed column A column packed with spherical particles provides high sur-

face area geometry that is useful in isolating speciﬁc protein(s) or other biological

molecules from a cell lysate mixture. The Ergun equation relates the pressure drop

through a packed bed of spheres to various ﬂuid and geometric parameters of the bed:

Δp

¼ 150

ð1  εÞ

μu

þ 1:75

ð1  εÞ

ρu

;

where Δp is the pressure drop, l is the length of the co lumn, ε is the porosity, μ is the

ﬂuid viscosity, u is the ﬂuid velocity, d

is the diameter of the spherical particles, and

Table 5.2. Nonlinea r root-ﬁnding methods

Property

Bisection

method

Regula-falsi

method

Newton’s

method Secant method

Fixed-point

iteration

Type of method bracketing bracketing open interval open interval open interval

Rate of

convergence

r =1

C = 0.5

r =1 r = 2 for

simple roots

r = 1 for

multiple roots;

if Equation

(4.25) is used

then r =2

C =

ðx



ðx





r = 1.618

C =

ðx



ðx





0:618

r =1

C =|g

(x)|

Number of initial

guesses required

2212 1

Is convergence

guaranteed as

i → ∞?

yes yes no no no

Other limitations cannot be

used to ﬁnd a

double root

cannot be

used to ﬁnd

a double

root

proximity of

guess value to

root to ensure

convergence

not known a

priori

proximity of guess

value to root to

ensure convergence

not known a priori

Convergence

observed only

if |g

(x)| < 1

349

5.10 Problems

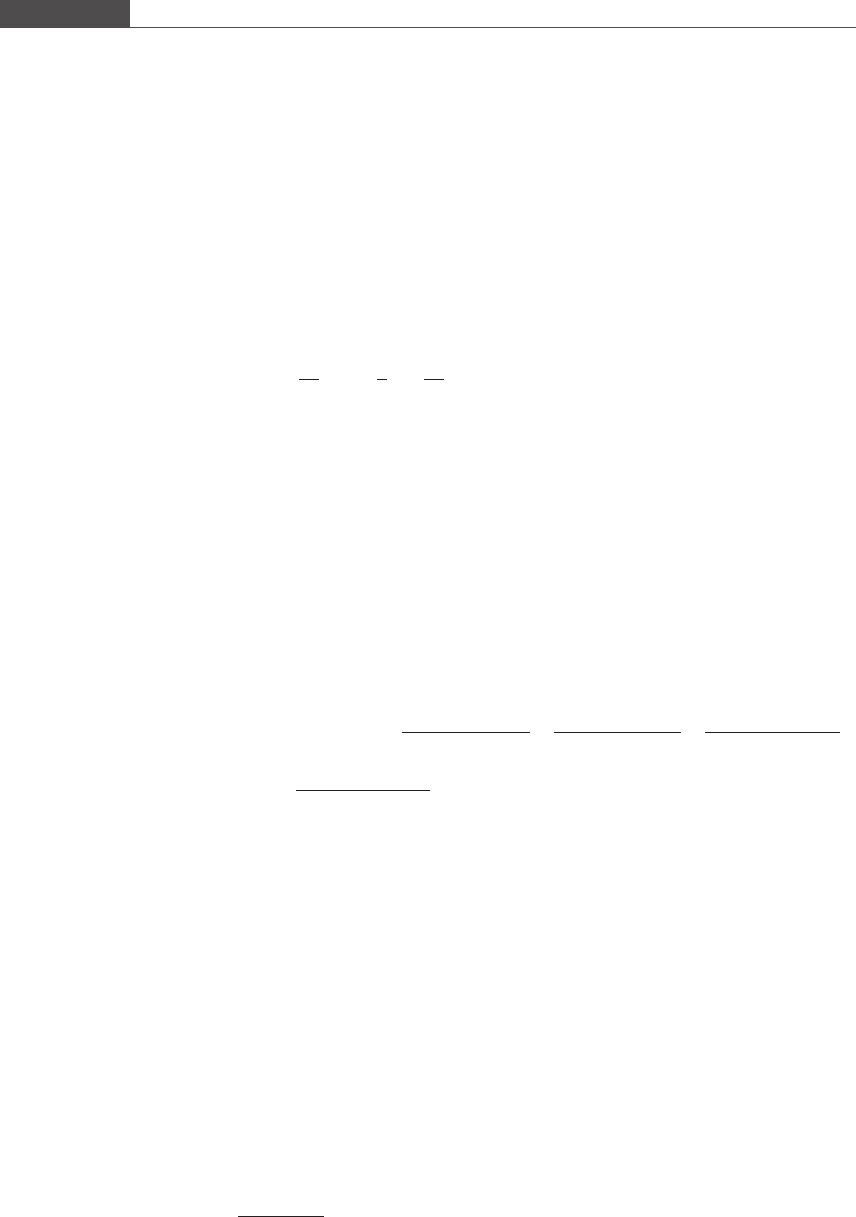
ρ is the ﬂuid density. For a 20 cm column, packed with 1 mm spheres and perfused

with a buffer of equal viscosity and density to water (μ = 0.01 P, ρ = 1 g/cm

), use

the bisection method to determine the column porosity if the pressure drop is

measured to be 810.5 dyn/cm

for a ﬂuid ﬂowing with velocity u = 0.75 cm/s.

Make sure that you use consistent units throughout your calculation.

Using a starting interval of 0.1 < ε < 0.9, report the number of iterations

necessary to determine the porosity to within 0.01 (tolerance).

5.2. Blood rheol ogy Blood behaves as a non-Newtonian ﬂuid, and can be modeled as

a “Casson ﬂuid.” This model predicts that unlike simple ﬂuids such as water, blood

will ﬂow through a tube such that the central core will move as a plug with little

deformation, and most of the velocity gradient will occur near the vessel wall. The

following equation is used to describe the plug ﬂow of a Casson ﬂuid:

FðξÞ¼1 

ﬃﬃﬃ

ξ 

;

where F measures the reduction in ﬂowrate (relative to a Newtonian ﬂuid) experi-

enced by the Casson ﬂuid for a given pressure gradient and ξ gives an indication of

what fraction of the tube is ﬁlled with plug ﬂow. For a value of F = 0.40, use the

secant method to determine the corresponding value of ξ. Use a starting guess of ξ =

0.25 (and a second starting guess of 0.26, since the secant method requires two init ial

guesses). Show that the rate of convergence is superlinear and approximately equal

to r = 1.618. Note that the function is not deﬁned when ξ ≤ 0. Therefore, one must

choose the starting guess values carefully.

5.3. Saturation of oxygen in water Oxygen can dissolve in water up to a saturation

concentration that is dependent upon the temperature of water. The saturation

concentration of dissolved oxygen in water can be calculated using the following

empirical equation:

ln s

¼139:34411 þ

1:575701  10



6:642308  10

1:243800  10



8:621949  10

;

where s

= the satur ation concentration of dissolved oxygen in water at 1 atm

(mg/l) an d T

= absolute temperature (K). Rem ember that T

= T

+ 273.15,

where T

= temperature (8C). According to this equation, saturation decreases with

increasing temperature. For typical water samples near ambient temperature, this

equation can be used to determine oxygen concen tration ranges from 14.621 mg/l at

0 8C to 6.949 mg/l at 35 8C. Given a value of oxygen concentration, this formula and

the bisection method can be used to solve for the temperature in degrees Celsius.

(a) If the initial guesses are set as 0 and 35 8C, how many bisection iterations would

be required to determine temperature to an absolute error of 0.05 8C?

(b) Based on (a), develop and test a bisection m-ﬁle function to determine T as a

function of a given oxygen concentration. Test your function for s

= 8, 10,

and 14 mg/l. Check your results.

5.4. Fluid permeability in biogels The speciﬁc hydraulic permeability k relates the

pressure gradient to the ﬂuid velocity in a porous medium such as agarose gel or

extracellular matrix. For non-cylindrical pores comprising a ﬁber matrix, k is given by

k ¼

20ð1  εÞ

;

350

Root-finding techniques for nonlinear equations

where r

is the ﬁber radius and 0 ≤ ε ≤ 1 is the porosity (Saltzman, 2001). For a ﬁber

radius of 10 nm and a measurement of k = 0.4655 nm

, determine the porosity using

both (i) the regula-falsi and (ii) the secant methods. Calculate the ﬁrst three iterations

using both methods for an initial interval of 0.1 ≤ ε ≤ 0.5 for regula-falsi, and init ial

guesses of ε

−1

= 0.5 and ε

= 0.55 for the secant method. What are the relative errors

in the solutions obtained at the third iteration?

5.5. Thermal regulation of the body Stolwijk (1980) developed a model for thermal

regulation of the human body, where the body is represented as a spherical segment

(head), ﬁve cylindrical segments (trunk, arms, hands, legs, and feet), and the central

blood compartment. An important mechanism of heat loss is the respiratory system.

To approximate the thermal energy contained in the breath, we use the following

mathematical model that relates the pressure of water vapor in the expired breath

(mm Hg) to temperature T,(8C) of the inhaled air:

¼ exp 9:214 

1049:8

1:985ð32 þ 1:8TÞ



If the water vapor in the expired breath is measured to be 0.298 mm Hg, then use

Newton’s method of nonlinear root ﬁnding to determine the inhaled gas temperature.

Use a starting guess of 15 8C. Conﬁrm your answer using the bisection method. Take

(5 8C, 20 8C) as your initial interval.

5.6. Osteoporosis in Chinese women Wu et al.(2003) studied the variations in age-

related speed of sound (SOS) at the tibia and prevalence of osteoporosis in native

Chinese women. They obtained the following relationship between the SOS and the

age in years, Y:

SOS ¼ 3383 þ 39:9Y  0:78Y

þ 0:0039Y

;

where the SOS is expressed in units of m/s. The SOS for one research subject is

measured to be 3850 m/s; use Newton’s method of nonlinear root ﬁnding to deter-

mine her most likely age. Take Y = 45 years as your initial guess.

5.7. Biomechanics of jumping The effort exerted by a person while jumping is depend-

ent on several factors that include the weight of the body and the time spent pushing

the body off the ground. The following equation describes the force F (measured in

pound-force, lb

) exerted by a person weighing 160 lb and performing a jump from a

stationary position. The time spent launching the body upwards, or the “duration of

lift-off,” is denoted by τ (in milliseconds):

FðtÞ¼480  sin

πt



þ 160 1  t=τðÞ:

For τ = 180 ms, use the regula-falsi method of nonlinear root ﬁnding to determine

the time at which the force is equal to 480 lb

. Use 1 < t < 75 as your initial interval.

5.8. Drug concentration proﬁle The following equation describes the steady state

concentration proﬁle of a drug in the tissue surrounding a spherical polymer

implant:

exp ðζ  1Þ½;

where C

(ζ) is the concentration in the tissue, C

is the concentration at the surface of

the implant,

 ¼ R

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



;

351

5.10 Problems

ζ = r/R is the dimensionless radial position, R is the radius of the implant, k

is the

apparent ﬁrst-order elimination constant, and D

is the apparent diffusivity of the

drug (Saltzman, 2001). For parameter values of R = 0.032 cm, k

= 1.9 × 10

4

/s,

and D

=4× 10

7

/s (typical values for experimental implants used to treat brain

tumors), use the secant method to solve for the dimensionless radial position, where

the concentration of drug is equal to half that at the implant surface. Determine the

ﬁrst two guess values by ﬁrst plotting the function. Why will the ﬁxed-point iterative

method not work here?

5.9. Using Equations (5.10) and (5.13), show that, for the ﬁxed-point iterative method,

lim

n!∞

C ¼ g



ðÞ

5.10. Animal-on-a-chip Box 2.1 discussed the concept of “animal-on-a-c hip” or the

microscale cell culture analog (μCCA) invented by Shuler and co-workers at Cornell

University as cost-effective in vitro drug-screening method. The transport and

metabolism of naphthalene was investigated within the μCCA assuming steady

state conditions. In our problem formulation discussed in Box 2.1, it was assumed

that the consumption rate of naphthalene in the lung and liver followed zero-order

kinetics, so that we could obtain a set of linear equations. Now we drop the

assumption of zero-order kinetics. Substituting the process parameters listed in

Box 2.1 into Equations (2.1) and (2.2), we have the following.

Lung compartment

780ð1  RÞþR 0:5C

liver

þ 1:5C

lung





8:75C

lung

2:1 þ C

lung

0:08  2C

lung

¼ 0:

Liver compartment

0:5C

lung



118C

liver

7:0 þ C

liver

0:322  0:5C

liver

¼ 0:

(a) For recycle fractions R = 0.6, 0.8, and 0.9, determine the steady state naphtha-

lene concentrations in the lung and liver compartments using the multi-equation

Newton’s method. Use as the initial guess values for C

lung

and C

liver

the solution

obtained from Problem 2.5, in which you solved for the naphthalene concen-

trations us ing linear solution methods, and zero-order kinetics was assumed for

naphthalene consumption. These are provided below:

R ¼ 0:6: C

lung

¼ 360:6 μ M; C

liver

¼ 284:6 μ M;

R ¼ 0:8: C

lung

¼ 312:25 μ M; C

liver

¼ 236:25 μ M;

R ¼ 0:9: C

lung

¼ 215:5 μ M; C

liver

¼ 139:5 μ M:

(b) Determine the steady state naphthalene concentrations in the lung and liver

compartments for R = 0.95. Can you use the solution from Problem 2.5 for

R = 0.9 as initial guess values? Why or why not? If not, ﬁnd other values to use

as initial guess values. Do you get a solution at R = 0.95 using the multi-

equation Newton’s method?

2.5 (listed above) for the three recycle ratios R = 0.6, 0.8, and 0.9. Why are the

steady state naphthalene concentrations higher when zero-order naphthale ne

consumption rate is not assumed? Find the relative error in the Problem 2.5

(linear) solutions listed above. What is the trend in relative error with R? Can

you explain this trend?

352

Root-finding techniques for nonlinear equations

References

Burden, R. L. and Faires, J. D. (2005) Numerical Analysis (Belmont, CA: Thomson Brooks/

Cole).

Fournier, R. L. (2007) Basic Transport Phenomena in Biomedical Engineering (New York:

Taylor & Francis).

Gaehtgens, P. (1980) Flow of Blood through Narrow Capillaries: Rheological Mechanisms

Determining Capillary Hematocrit and Apparent Viscosity. Biorheology, 17, 183–9.

Gaehtgens, P., Duhrssen, C., and Albrecht, K. H. (1980) Motion, Deformation, and

Interaction of Blood Cells and Plasma During Flow through Narrow Capillary Tubes.

Blood Cells, 6, 799–817.

Lauffenburger, D. A. and Linderman, J. J. (1993) Receptors: Models for Binding, Trafﬁcking

and Signaling (New York: Oxford University Press).

McCabe, W., Smith, J., and Harriott, P. (2004) Unit Operations of Chemical Engineering (New

York: McGraw-Hill).

Mody, N. A. and King, M. R. (2008) Platelet Adhesive Dynamics. Part II: High Shear-

Induced Transient Aggregation Via GPIbalpha-vWF-GPIbalpha Bridging. Biophys. J.,

95, 2556–74.

Perelson, A. S. (1981) Receptor Clustering on a Cell-Surface. 3. Theory of Receptor Cross-

Linking by Multivalent Ligands – Description by Ligand States. Math. Biosci., 53, 1–39.

Saltzman, W. M. (2001) Drug Delivery: Engineering Principles for Drug Therapy (New York:

Oxford University Press).

Stolwijk, J. A. (1980) Mathematical Models of Thermal Regulation. Ann. NY Acad. Sci., 335,

98–106.

Wu, X. P., Liao, E. Y., Luo, X. H., Dai, R. C., Zhang, H., and Peng, J. (2003) Age-Related

Variation in Quantitative Ultrasound at the Tibia and Prevalence of Osteoporosis in

Native Chinese Women. Br. J. Radiol., 76, 605–10.

353

5.10 Problems

6 Numerical quadrature

6.1 Introduction

Engineering and scientiﬁc calculations often require the evaluation of integrals. To

calculate the total amount of a quantity (e.g. mass, number of cells, or brightness of

an image obtained from a microscope/camera) that continuously varies with respect

to an independent variable such as location or time, one must perform integration.

The concentration or rate of the quantity (e.g. concentration of substrate or drug,

intensity of light passing through a microscope, position-dependent density of a

material) is integrated with respect to the independent variable, which is called the

integration variable. Integration is the inverse of differentiation. A derivative mea-

sures the rate of change of a quan tity, e.g. the speed of travel vðtÞ is obtained by

measuring the change in distance s with respect to time elapsed, or vtðÞ¼ds=dt.

A deﬁnite integral I, on the other hand, is a multiplicative operation and calculates

the product of a function with an inﬁnitesimal increment of the independent varia-

ble, summed continuously over an interval, e.g. the distance traveled is obtained by

integrating speed over an interval of time, or s ¼

vtðÞdt. The integration process

seeks to ﬁnd the function gðxÞ when its derivative g

ðxÞ is provided. Therefore, an

integral is also called an anti-derivative, and is deﬁned below.

I ¼ gxðÞ¼

xðÞdx ¼

fxðÞdx;

where fðxÞis called the integrand, x is the variable of integration such that a  x  b,

and a and b are the limits of integration. If the integrand is a well-behaved, conti-

nuous function, i.e. it does not become inﬁnite or exhibit discontinuities within the

bounds of integration, an analytical solution to the integral may exist. An analytical

solution is the preferred method of solution because it is exact, and the analytical

expression can lend insight into the process or system being investigated. The effects

of modifying any of the process parameters are straightforward and intuitive.

However, not all integrals are amenable to an analytical solution. Analytical

solutions to integrals do not exist for certain integrand functions or groups of

functions, i.e. the anti-derivative of some functions are not deﬁned. Or, it may be

impossible to evaluate an integral analytically because the function becomes singular

(blows up) at some point within the interval of integration, or the function is not

continuous. Even if an analytical solution does exist, it may happen that the solution

is too time-consuming to ﬁnd or difﬁcult to compute. Sometimes, the functional

form of the integrand is unknown and the only available information is a discrete

data set consisting of the value of the function at certain values of x, the integration

variable. When any of the above situations are encountered, we use numerical

methods of integration to obtain the value of the deﬁnite integral. The use of

numerical methods to solve a deﬁnite integral is called numerical quadrature.

A graphical description best illustrates the process of integrati on. The deﬁnite

integral represents an area that lies under a curve described by the function fðxÞ, and

which is bounded on either side by the limits of integration. This is shown in

Figure 6.1. The result of evaluating a deﬁnite integral is a number which has units

equal to f·x, and is a unique solution.

Suppose we have values of the function fðx

Þ i 2 0; 1; ...; nðÞspeciﬁed at n +1

points, i.e. at x

; x

; ...; x

. Numerical quadrature proposes an approximate solu-

tion to the integral of interest according to the formula given below:

fxðÞdx 

i¼0

ðÞ: (6:1)

The known function values fx

ðÞare multiplied by suitable weights and are summed

to yield the numerical approximation. The weights that are used in the formula

depend on the quadrature method used.

In any numerical method of integration, the functional form of the integrand

is replaced with a simpler function called an interpolant or inter pol ati ng functi on.

The latter function is integrated in place of the original function, and the result

yields the numerical solution. The interpolating function ﬁts the data exactly at

speciﬁc or known data points and interpolates the data at intermediate values.

Speciﬁcally, the interpolant passes through either (1) the supplied data points if

only a discrete data set is available, or ( 2) the function evaluated at discrete

points called node s within the interval, if an analytic al form of the integrand is

available. The interpolating function approximates the behavior of fðxÞ as a

function of x.

Suppose we are given n + 1 function values fx

ðÞat n + 1 equally spaced values,

¼ a þ ih, within the interval a  x  b. Accordingly, x

¼ a and x

¼ b. The

entire interval ½a; b is now divided into n subintervals ½x

; x

iþ1

. The width of each

subinterval is h ¼ x

iþ1

 x

. Within each subinterval x

 x  x

iþ1

, suppose the

function fxðÞis approximated by a zeroth-degree polynomial, which is a constant.

Let the value of the constant in any subinterval be equal to the function evaluated at

the midpoint of the subinterval, fx

iþ0:5

ðÞ. Over any particular subinterval, the

integral can be approximated as

iþ1

fxðÞdx ¼ fx

iþ0:5

ðÞ

iþ1

dx ¼ fx

iþ0:5

ðÞh:

Figure 6.1

Graphical interpretation of the process of integration.

(x)

= ∫f(x)dx

Area under the curve

355

6.1 Introduction

Since

fxðÞdx ¼

fxðÞdx þ

fxðÞdx þþ

n1

fxðÞdx;

we obtain the numerical formula for the integral

fxðÞdx ¼ h

n1

i¼0

iþ0:5

ðÞ: (6:2)

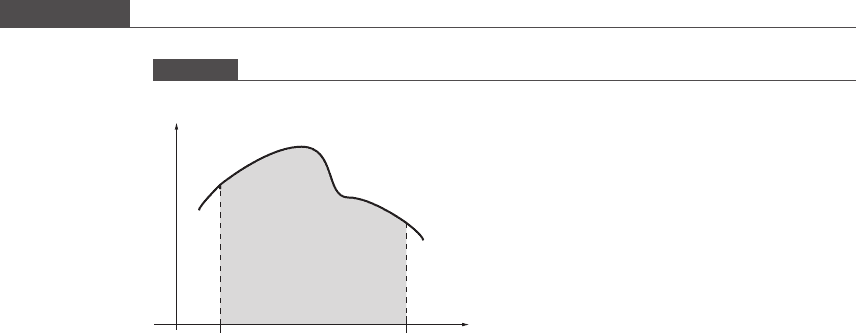
Equation (6.2) is called the composite midpoint rule and is demonstrated in

Figure 6.2. The midpoint rule falls under the Newton–Cotes rules of integration

which are discussed in Section 6.3. The term “composite” is used because the

midpoint rule is evaluated multiple times over sequential segments of the interval.

The composite midpoint rule substitutes f ðxÞ with a piecewise constant function.

Note that as we increase the number of sub intervals, the accuracy in approximating

fðxÞ will improve. As n ! ∞, our numerical result will become exact (limited by

round-off error). However, if we were to ﬁnd the function value at the midpoint

ða þ bÞ=2 of the interval ½a; b and simply multiply that by the width of the interval

b  a, then our numerical approximation is likely to be quite inaccurate.

In this chapter, we focus on the use of polynomial interpolating functions to

approximate the true function or integrand. The interpolating polynomial pðxÞ is

constructed so that it coincides with the original function at the n + 1 node points;

pðxÞ approximates the behavior of fðxÞ at all points between the known values.

A polynomial has the distinct advantage that it can be easily integrated. It is there-

fore popularly used to develop numerical integration schemes. The entire interval of

integration is divided into several subintervals. The data are approximated by a

piecewise polynomial interpolating function. In piecewise interpolation, a different

interpolating function is constructed for each subinterval. Each subinterval is then

integrated separately, i.e. each polynomial function is integ rated only over the range

of x values or the subinterval on which it is deﬁned. The numerical formula for

integration, the order of the numerical method, and the magnitude of truncation

error depend on the degree of the interpolating polynomial.

Function values may be evaluated at neither of the endpoints, one or both

endpoints of the interval, and/or multiple points inside the interval. Sometimes,

the function value at the endpoint of an interval may become inﬁnite, or endpoint

Figure 6.2

The composite midpoint rule.

f(x)

Midpoint of 3rd subinterval

2.5

, f(x

2.5

))

356

Numerical quadrature