King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

Integrating the differential equation

We wish to integrate z from 50 cm to 5 cm. Integrating the left-hand side from 0 to t, we obtain

t ¼



α þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ 8gðz þ LÞ



α þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ 8gðz þ LÞ



dz:

The quadrature method chosen is the composite trapezoidal rule. Two programs were written to compute

the integral. Program 6.1 is the trapezoidal integration routine and Program 6.2 calculates the integrand

function for any value of z. The function routine to calculate the integrand has been vectorized to allow

input of a vector variable.

Typing into the MATLAB Command Window

trapezoidal_rule(‘IVdrip’,5, 50, 9)

the output is

0.5751

The time taken for 90% of the bag to empty is given by

t ¼

0:5751ðÞ;

which is equal to 46 008 seconds or 12.78 hours.

MATLAB program 6.1

function I = trapezoidal_rule(integrandfunc, a, b, n)

% This function uses the composite trapezoidal rule to calculate an

% integral when an analytical function for the integrand

is speciﬁed.

% Input variables

% integrandfunc : function that calculates the integrand

% a : lower limit of integration

% b : upper limit of integration

% n : number of subintervals

% Output variables

% I : value of integral

x = linspace(a, b, n + 1); % n + 1 nodes created within the interval

y = feval(integrandfunc, x);

h = (b-a)/n;

I = h/2*(y(1) + y(n+1) + 2*sum(y(2:n)));

MATLAB program 6.2

function f = IVdrip(z)

% This function calculates the integrand function of the IV drip problem.

% Parameters

377

6.3 Newton–Cotes for mulas

L = 91.44; % cm

mu = 0.01; % Poise

d = 0.1; % cm

rho = 1; % g/cm^3

alpha = 64*L*mu/d^2/rho;

g = 981; % cm/s^2

f = 1./(-alpha + sqrt(alpha^2 + 8*g*(z + L)));

Box 6.1B Solute transport through a porous membrane

The integral in Equation (6.7) can be solved by numerically integrating the integrand defined by

Equations (6.8) and (6.9). Calculation of ΔG is not straightforward, but also not too difficult. Note that the

term Λ is defined by an infinite series. The MATLAB software contains the functions besseli and

besselk to calculate the modified Bessel function of any order. Program 6.3 calculates the

integrand. Program 6.1 above is used to perform the numerical integration for different numbers of

subintervals, n = 5, 10, and 20:

alpha = 0.25;

trapezoidal_rule(‘partition_coefﬁcient’,0, 1–alpha, 5)

ans =

0.0512

We double the number of subintervals to obtain

trapezoidal_rule(‘partition_coefﬁcient’,0, 1–alpha, 10)

MATLAB calculates

ans =

0.0528

Again, on redoubling the number of subintervals we obtain

trapezoidal_rule(‘partition_coefﬁcient’,0, 1–alpha, 20)

MATLAB calculates

ans =

0.0532

The radially averaged concentration of solute within a pore when the solute concentration is the same

on both sides of the membrane (no solute gradient) is 0.0532 × C

, or approximately 5% of the bulk

solute concentration. The pore excludes 95% of solute particles that otherwise would have occupied the

pore region if steric and electrostatic effects were absent!

If we assume that the solution for n = 20 is correct, the error in the first solution using five

subintervals is 0.0020 and is 0.0004 when ten subintervals are used (second solution). The ratio of the

errors obtained for n = 10 and n =5is





The error difference agrees with the second-order truncation error (Equation 6.23) of the composite

trapezoidal rule.

378

Numerical quadrature

MATLAB program 6.3

function f = partition_coefﬁcient(beta)

% This function calculates

% (1) the dimensionless potential energy of interaction between the

% solute and pore wall, and

% (2) the integrand function that characterizes solute distribution

% within the pore.

% Input variables

% beta : dimensionless radial position of sphere center in tube

% Parameters

kB = 1.38e-23; % J/molecule/deg K : Boltzmann constant

T = 273 + 37; % deg K : temperature

R = 8.314; % J/mol/deg K : gas constant

F = 96485.34; % Coulomb/mol : Faraday constant

eps0 = 8.8542e-12; % C/V/m : dielectric permittivity of free space

releps = 74; % solvent relative dielectric permittivity

deltabar = 0.1; % ratio of sphere to solvent dielectric constant

R0 = 20e-9; % m : pore radius

Cinf = 0.01*1000; % mol/m^3 : electrolyte concentration

alpha = 0.25; % dimensionless sphere radius

qs = 0.01; % C/m^2 : sphere surface charge density

qc = 0.01; % C/m^2 : cylinder surface charge density

% Additional calculations

abseps = releps*eps0; % absolute solvent dielectric permittivity

sigmas = F*R0*qs/abseps/R/T; % dimensionless surface charge density

sigmac = F*R0*qc/abseps/R/T; % dimensionless surface charge density

% Calculation of tau: ratio of pore radius to Debye length

tau = R0*sqrt(F^2/abseps/R/T*2*Cinf);

% Calculation of lambda

% Calculation of inﬁnite series

t=0;ﬁrstterm = 0; total = 0; lastterm = 1;

% If difference between new term and ﬁrst term is less than 0.001*ﬁrst

% term

while lastterm > (0.001*ﬁrstterm)

preterm = (beta.^t)*factorial(2*t)/(2^(3*t))/((factorial(t))^2);

lastterm = preterm.*besseli(t, tau*beta)* ...

(tau*besselk(t + 1, 2*tau) + 0.75*besselk(t, 2*tau));

if t == 0

ﬁrstterm = lastterm;

end

total = lastterm + total;

t=t+1;

end

lambda = pi/2*besseli(0, tau*beta).*total;

% Calculating the Langevin function

L = coth(tau*alpha)–1/tau/alpha;

379

6.3 Newton–Cotes for mulas

6.3.2 Simpson’s 1/3 rule

Simpson’s 1/3 rule is a closed numerical integration scheme that approximates the

integrand function with a quadratic polynomial. The second-degree polynomial is

constructed using three function values: one at each endpoint of the integration

interval and one at the interval midpoint. The function is evaluated at x

; x

; and x

where x

,andx

and x

specify the endpoints of the interval. The entire

integration interval is effectively divided into two subintervals of equal width:

 x

¼ x

 x

¼ h. The integ ration interval is of width 2h. The formula for a

second-degree polynomial interpolant is given by Equation (6.14), which is repro-

duced below:

pxðÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞþ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞ:

The interpolating equation above contains three second-order Lagrange polynomials,

which upon integration yield the weights of the numerical integration formula. The

integral of the function is equal to the integral of the second-degree polynomial

interpolant plus the integral of the truncation error associated with interpolation, i.e.

fxðÞdx ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

ðÞþ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ



x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ



000

ξðxÞðÞ

x  x

ðÞx  x

ðÞdx; a  ξ  b:

% Calculating the interaction energy

delGnum1 = 8*pi*tau*alpha^4*exp(tau*alpha)/((1+tau*alpha)^2)* ...

lambda*sigmas^2;

delGnum2 = 4*pi^2*alpha^2*besseli(0, tau*beta)/ ...

(1 + tau*alpha)/besseli(1,tau)*sigmas*sigmac;

delGnum3 = (pi*besseli(0, tau*beta)/tau/besseli (1, tau)).^2 * ...

(exp(tau*alpha)–exp(-tau*alpha))* ...

tau*alpha*L/(1 + tau*alpha)*sigmac^2;

delGnum = delGnum1 + delGnum2 + delGnum3;

delGden = pi*tau*exp(-tau*alpha)–2*(exp(tau*alpha)– ...

exp(-tau*alpha)) * ... tau*alpha*L*lambda/(1 + tau*alpha);

delG = delGnum./delGden;

% Calculating the dimensional interaction energy

E = R0*(R*T/F)^2*abseps*delG;

% Calculating the integrand

f = 2*exp(-E/kB/T).*beta;

380

Numerical quadrature

Performing integration of the ﬁrst term of the interpolant pðxÞ, we obtain

¼ fx

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

dx;

and after some algebraic manipulation we obtain

 x

ðÞ

=2 ð2x

þ x

Þ=6ðÞ

 x

ðÞx

 x

ðÞ

ðÞ:

Substituting x

¼ x

þ 2h and x

¼ x

þ h into the above, I

simpliﬁes to

ðÞ:

Integration of the second term,

¼ fx

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

dx;

yields

¼

 x

ðÞ

6 x

 x

ðÞx

 x

ðÞ

ðÞ:

Again, the uniform step size allows us to simplify the integral as follows:

ðÞ:

On integrating the third term,

¼ fx

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

dx;

we get

 x

ðÞ

ðx

þ 2x

Þ=6  x

=2ðÞ

 x

ðÞx

 x

ðÞ

ðÞ:

Deﬁning x

and x

in terms of x

and the uniform step size h, I

becomes

ðÞ:

The numerical formula for the integral is thus given by

fxðÞdx  I ¼ I

þ I

ðÞþ4fx

ðÞþfx

ðÞðÞ:

(6:25)

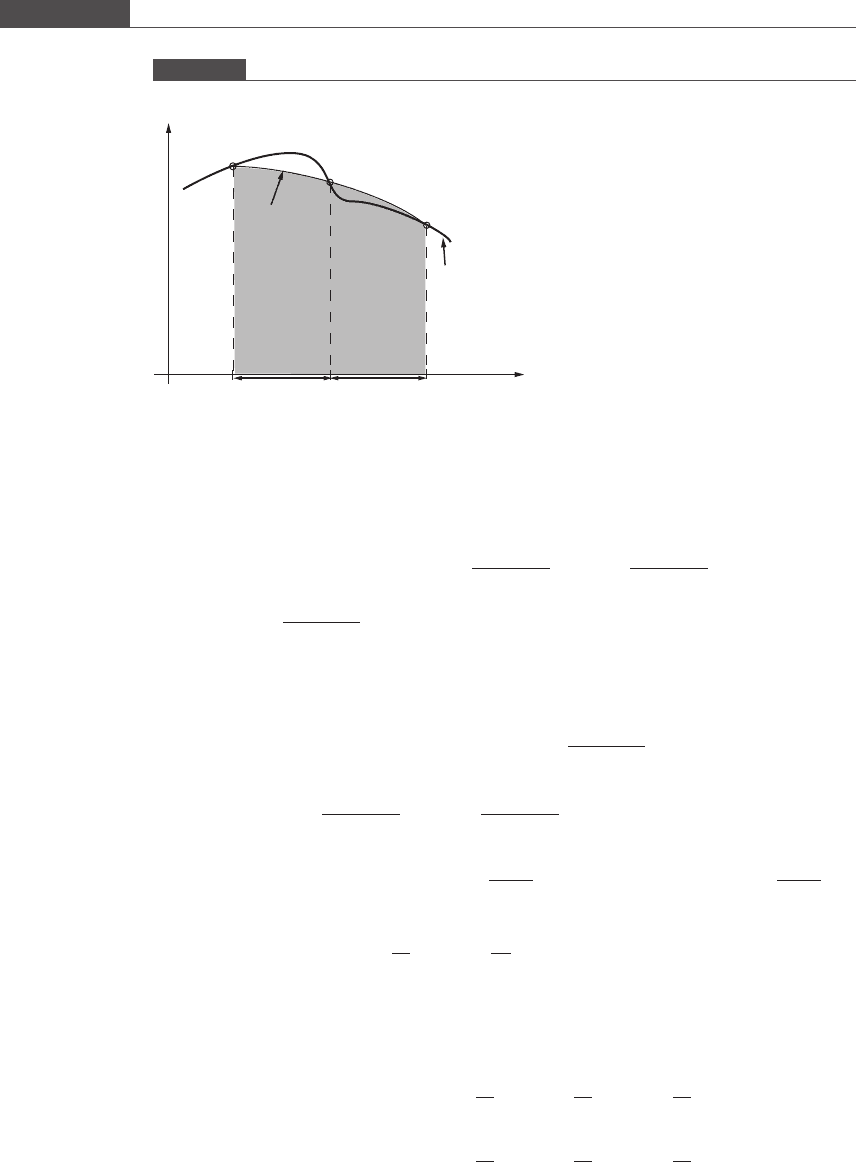
Equation (6.25) is called Simpson’s 1/3 rule. Figure 6.13 demonstrates graphically

the numerical integration of a function using Simpson’s 1/3 rule.

We cannot take f

000

ξðxÞðÞout of the error term integral since it is a function of the

integration variable. Subsequent integration steps that retain this term in the integral

require complex manipulations that are beyond the scope of this book. (The inter-

ested reader is referred to Patel (1994), where the integration of this term is

381

6.3 Newton–Cotes for mulas

demonstrated.) To obtain the error term of Simpson’s 1/3 rule, we look to the Taylor

series expansion.

Using the Taylor series, we expand the integrand function fðxÞabout the midpoint

of the interval x

fxðÞ¼fx

ðÞþx  x

ðÞf

ðÞþ

x  x

ðÞ

ðÞþ

x  x

ðÞ

000

ðÞ

x  x

ðÞ

ð4Þ

ξ xðÞðÞ;

where ξ 2 x

; x½.

Integrating the above expansion,

fxðÞdx ¼

þh

h

ðÞþx  x

ðÞf

ðÞþ

x  x

ðÞ

x  x

ðÞ

000

ðÞþ

x  x

ðÞ

ð4Þ

ξ xðÞð



¼ 2hf x

ðÞþ0  f

ðÞþ

2 h

ðÞ

2:3

ðÞþ0  f

000

ðÞþf

ð4Þ

ðÞ

2 h

ðÞ

5  4!

;

fxðÞdx ¼ 2hf x

ðÞþ

ð4Þ

ðÞ; (6:26)

where ξ

2 a; b½.

Now we expand the function at the endpoints of the interval about x

using the

Taylor seri es:

faðÞ¼fx

ðÞ¼fx

ðÞhf

ðÞþ

ðÞ

000

ðÞþ

ð4Þ

ðÞ;

ðÞ

¼ fx

ðÞ

¼ fx

ðÞ

þ hf

ðÞ

000

ðÞ

ð4Þ

ðÞ

The above expressions for fx

ðÞand fx

ðÞare substituted into Equation (6.25) to yield

Figure 6.13

Graphical description of Simpson’s 1/3 rule.

y = f(x)

= p(x)

h h

, f(x

))

, f(x

))

, f(x

))

382

Numerical quadrature

I ¼

6fx

ðÞþh

ðÞþ

ð4Þ

ðÞþf

ð4Þ

ðÞ





: (6:27)

Let f

ð4Þ

ξðÞ¼max f

ð4Þ

ξ xðÞðÞ





for a  ξ  b. Subtracting Equation (6.27) from

Equation (6.26), the integration error is found to be

E  f

4ðÞ

ξðÞ





¼

4ðÞ

ξðÞ: (6:28)

The error is proportional to the subinterval width h raised to the ﬁfth power.

Simpson’s 1/3 rule is a ﬁfth-order method. You can compare this with the trapezoi-

dal rule, which is a third-order method. Since the error term contains the fourth

derivative of the function, this means that Simpson’s rule is exact for any function

whose fourth deriva tive over the entire interval is exactly zero. All polynomials of

degree 3 and less have a fourt h derivative equal to zero. It is interesting to note that,

even though we interpolated the function using a quadratic polynomial, the rule

allows us to integrate cubics exactly due to the symmetry of the interpolating

function (cubic errors cancel out).

The degree of precision of Simpson’s 1/3 rule is 3. The error of Simpson’s 1/3 rule is Oh



The accuracy of the numerical integration routine can be greatly improved if the

integration interval is subdivided into smaller intervals and the quadrature rule is

applied to each pair of subintervals. A requirement for using Simpson’s 1/3 rule is

that the interval must contain an even number of subintervals. Numerical integra-

tion using piecewise quadratic functions to approximate the true integrand function,

with equal subinterval widths, is called the composite Simps on’s 1/3 method.

The integration interval has n subintervals, such that x

¼ x

þ ih, x

 x

i1

¼ h,

and i =0,1,2, ..., n. Since n is even, two con secutive subintervals can be paired to

produce n/2 such pairs (such that no subint erval is repeated). Summing the integrals

over the n/2 pairs of subintervals we recover the original integ ral:

fxðÞdx ¼

n=2

i¼1

2ði1Þ

fxðÞdx:

Simpson’s 1/3 rule (Equation (6.25)) is applied to each of the n/2 subintervals:

fxðÞdx ¼

n=2

i¼1

2i2

ðÞþ4fx

2i1

ðÞþfx

ðÞðÞ

4ðÞ

ðÞ



;

where ξ

2 x

2i2

; x

½is a point located within the ith subinterval pair. Note that the

endpoints of the paired subintervals x

2i2

; x

½, except for the endp oints of the

integration interval x

; x

½, are each repeated twice in the summation since each

endpoint belongs to both the previous subinterval pair and the next subinterval pair.

Accordingly, the formula simpliﬁes to

fxðÞdx ¼

ðÞþ2

ðn=2Þ1

i¼1

ðÞþ4

n=2

i¼1

2i1

ðÞþfx

ðÞ

n=2

i¼1



4ðÞ

ðÞ



The numerical integration formula for the composite Simpson’s 1/3 rule is given by

383

6.3 Newton–Cotes for mulas

fxðÞdx 

ðÞþ2

ðn=2Þ1

i¼1

ðÞþ4

n=2

i¼1

2i1

ðÞþfx

ðÞ

: (6:29)

Next, we evaluate the error term of integration. The average value of the fourth

derivative over the interval of integration is deﬁned as follows:

ð4Þ

n=2

i¼1

ð4Þ

ðÞ;

and

E ¼



ð4Þ

Since n ¼ðb  aÞ=h, the error term becomes

E ¼

ðb  aÞ

180

ð4Þ

; (6:30)

which is Oh



. The error of the composite Simpson’s 1/3 rule has a fourth-order

dependence on the distance h between two uniformly spaced nodes.

6.3.3 Simpson’s 3/8 rule

Simpson’s 3/8 rule is a Newton–Cotes closed integration formula that uses a cubic

interpolating polynomial to approximate the integrand function. Suppose the func-

tion values fðxÞ are known at four uniformly spaced poin ts x

; x

; and x

within

the integrati on interval, such that x

and x

are located at the interval endpoints,

and x

are located in the interior, such that they trisect the interval,

i.e. x

 x

¼ x

 x

¼ x

 x

¼ h. The integration interval is of width 3h.

A cubic polynomial can be ﬁtted to the function values at these four points to

generate an interpolant that approximates the function. The formula for a third-

degree polynomial interpolant can be constructed using the Lagrange polynomials:

pxðÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞx

 x

ðÞ

ðÞþ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞx

 x

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞx

 x

ðÞ

ðÞþ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞx

 x

ðÞ

ðÞ:

The cubic interpolant coincides exactly with the function f ðxÞ at the four equally

spaced nodes. The interpolating equation above contains four third-order Lagrange

polynomials, which upon integration yield the weights of the numerical integration

formula. The integral of fðxÞ is exactly equal to the integral of the co rresponding

third-degree polynomial interpolant plus the integral of the truncation error asso-

ciated with interpolation. Here, we simply state the numerical formula that is

obtained on integration of the polynomial pðxÞ over the interval (the proof is left

to the reader):

fxðÞdx 

ðÞþ3fx

ðÞþfx

ðÞðÞ: (6:31)

384

Numerical quadrature

Equation (6.31) is called Simpson’s 3/8 rule. For this rule, h ¼ðb  aÞ=3. The error

associated with this numerical formula is

E ¼

4ðÞ

ξðÞ: (6:32)

The error associated with Simpson’s 3/8 rule is Oh



, which is of the same order as Simpson’s 1/3

rule. The degree of precision of Simpson’s 3/8 rule is 3.

If the integration interval is divided into n > 3 subintervals, Simpson’s 3/8 rule can

be applied to each group of three consecutive subintervals. Thus, the integrand

function is approximated using a piecewise cubic polynomial interpolant.

However, to apply Simpson’s 3/8 rule, it is necessary for n to be divisible by 3. The

composite Simpson’s 3/8 formula is as follows:

fxðÞdx 

ðÞþ3

n=3

i¼1

3i2

ðÞþfx

3i1

ðÞ½þ2

ðn=3Þ1

i¼1

ðÞþfx

ðÞ

(6:33)

The truncation error of Equation (6.33) is

E ¼

ðb  aÞ

4ðÞ

: (6:34)

Since the truncation errors of the composite Simpson’s 1/3 rule and the composite

Simpson’s 3/8 rule are of the same order, both methods are often combined so that

restrictions need not be imposed on the number of subintervals (such as n must be

even or n must be a multiple of 3). If n is even, only the composite Simpson’s 1/3 rule

needs to be used. However, if n is odd, Simpson’s 3/8 rule can be used to integrate the

ﬁrst three subintervals, while the remainder of the interval can be integrated using

composite Simpson’s 1/3 rule. The use of the 1/3 rule is preferred over the 3/8 rule

since fewer data points (or functional evaluations) are required by the 1/3 rule to

achieve the same level of accuracy.

In Simpson’s formulas, since the nodes are equally spaced, the accuracy of

integration will vary over the interval. To achieve a certain level of accuracy, the

largest subinterval width h within the most difﬁcult region of integration that

produces a result of sufﬁcient accuracy ﬁxes the global step size. This subinterval

width must be applied over the entire interval, which unnecessarily increases the

number of subintervals required to calculate the integ ral. A more advanced algo-

rithm is the adaptive quadrature method, which selectively narrows the node spacing

when the accuracy condition is not met for a particular subinterval. The numerical

integration is performed twice for each subinterval, at a node spacing of h and at a

node spacing of h/2. The difference betw een the two integrals obtained with different

n (one twice the other) is used to e stimate the truncation error. If the error is greater

than the speciﬁed tolerance, the subinterval is halved recursively, and integration is

performed on each half by doubling the number of subintervals. The truncation

error is estimated based on the new node spacing and the decision to subdivide the

subinterval further is made accordingly. This procedure continues until the desired

accuracy level is met throughout the integration interval.

385

6.3 Newton–Cotes for mulas

Box 6.1C Solute transport through a porous membrane

The integral in Equation (6.7) can be solved by numerically integrating the function defined by

Equations (6.8) and (6.9) using Simpson’s 1/3 and 3/8 methods used in conjunction. Program 6.4

lists the function code that performs numerical integration using combined Simpson’s 1/3 rule and 3/8

rule so that any number of subintervals may be considered. The integration of Equation (6.7) is

performed for n = 5, 10, and 20. The numerical solutions obtained are as follows:

n ¼ 5: I ¼ 0:0546813;

n ¼ 10: I ¼ 0:0532860;

n ¼ 20: I ¼ 0:0532808:

The radially averaged concentration of solute within a pore when the solute concentration is the same

on both sides of the membrane is approximately 5% of the bulk solute concentration. With Simpson’s

rule, the solution converges much faster.

MATLAB program 6.4

function I = simpsons_rule(integrandfunc, a, b, n)

% This function uses Simpson’s 3/8 rule and composite Simpson ’ s 1/3

% rule to compute an integral when the analytical form of the

% function is provided.

% Input variables

% integrandfunc : function that calculates the integrand

% a : lower limit of integration

% b : upper limit of integration

% n : number of subintervals.

% Output variables

% I : value of integral

x = linspace(a, b, n + 1); % n + 1 nodes created within the interval

y = feval(integrandfunc, x);

h = (b-a)/n;

% Initializing

I1 = 0; I2 = 0; k = 0;

% If n is odd, use Simpson’s 3/8 rule ﬁrst

if mod(n,2)~=0 % n is not divisible by 2

I1 = 3*h/8*(y(1) + 3*y(2) + 3*y(3) + y(4));

k = 3; % Placeholder to locate start of integration using 1/3 rule

end

% Use Simpson’s 1/3 rule to evaluate remainder of integral

I2 = h/3*(y(1+k) + y(n+1) + 4*sum(y(2+k:2:n)) + 2*sum(y(3+k:2:n-1)));

I=I1+I2;

386

Numerical quadrature