King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

Using MATLAB

The MATLAB function quad performs numerical quadrature using an adaptive

Simpson’s formula. The formula is adaptive because the subinterval width is

adjusted (reduced) while integrating to obtain a result within the speciﬁed absolute

tolerance (default: 1 × 10

−6

) during the integration. The syntax for the function is

I = quad(‘integrand_function’,a,b)

I = quad(‘integrand_function’, a, b, Tol)

where a and b are the limits of integration and Tol is the user-speciﬁed absolute

tolerance. The function handle supplied to the quad function must be able to accept

a vector input and deliver a vector output.

6.4 Richardson’s extrapolation and Romberg integration

The composite trapezoidal formula for equal subinterval widths is a low-order

approximation formula, since the leading order of the error term is Oh



. The

truncation error of the composite trapezoidal rule follows an inﬁnite series consist-

ing of only even powers of h:

fxðÞdx 

ðÞþ2

n1

i¼1

ðÞþfx

ðÞ

¼ c

þ c

þ;

(6:35)

the proof of which is not given here but is discussed in Ralston and Rabinowitz

(1978). Using Richardson’s extrapolation technique it is possible to combine the

numerical results of trapezoidal integration obtained for two different step sizes,

and h

, to obtain a numerical result, I

¼ fI

; I

ðÞ, that is much more accurate than

the two approximations I

and I

. The higher-order integral approximation

obtained by combining the two low-accuracy approximations of the trapezoidal

rule has an error whose leading order is Oh



. Thus, using the extrapolation

formula, we can reduce the error efﬁciently by two orders of magnitude in a singl e

step. The goal of the extrapolation method is to combine the two integral approxi-

mations in such a way as to eliminate the lowest-order error term in the error series

associated with the numerical result I

Suppose the trapezoidal rule is used to solve an integral over the interval ½a; b.

We get the numerical result Ih

ðÞfor subinterval width h

subintervals), and the

result Ih

ðÞfor subinterval width h

subintervals). If I

is the exact value of the

integral, and the error associated with the result Ih

ðÞis Eh

ðÞ, then

¼ Ih

ðÞþEh

ðÞ: (6:36)

Equation (6.23) deﬁnes the truncation error for the composite trapezoidal rule. We

have

ðÞ¼

ðb  aÞh

If the error associated with the result Ih

ðÞis Eh

ðÞ, then

¼ Ih

ðÞþEh

ðÞ (6:37)

387

6.4 Richardson’s extrapolation and Romberg integration

and

ðÞ¼

ðb  aÞh

If the average value of the second derivative

over all nodes within the entire

interval does not change with a decrease in step size, then we can write Eh

ðÞ¼ch

and Eh

ðÞ¼ch

On equating Equations (6.3 6) and (6.37),

ðÞþch

 Ih

ðÞþch

;

we obtain

c 

ðÞIh

ðÞ

 h

Substituting the expression for c into Equations (6.36) or (6.37),



ðh

ÞIh

ðÞIh

ðÞ

ðh

Þ1

The scheme to combine two numerical integral results that have errors of the same order of magnitude

such that the combined result has a much smaller error is called Richardson’s extrapolation.

If h

¼ h

=2, the above equation simpliﬁes to



ðÞ

ðÞ: (6:38)

In fact, Equation (6.38) is equivalent to the composite Simps on’s 1/3 rule

(Equation (6.29)). This is shown next. Let n be the number of subintervals used to

evaluate the integral when using step size h

;2n is the number of subintervals used to

evaluate the integral when using step size h

According to the trapezoidal rule,

ðÞ¼

ðÞþ2

n1

i¼1

ðÞþfx

ðÞ

and

ðÞ¼

ðÞþ2

2n1

i¼1

ðÞþfx

ðÞ

Combining the above two trapezoidal rule expressions according to Equation (6.38),

we obtain



ðÞ

ðÞ¼

ðÞþ2

n1

i¼1

ðÞþ

i¼1

2i1

ðÞ

þ fx

ðÞ



ðÞþ2

n1

i¼1

ðÞþfx

ðÞ

;

which recovers the composite Simpson’s 1/3 rule,



ðÞþ2

n1

i¼1

ðÞþ4

i¼1

2i1

ðÞþfx

ðÞ

388

Numerical quadrature

The error associated with the composite Simpson’s 1/3 rule is Oh



. The error in

Equation (6.38) is also Oh



. This can be shown by combining the terms in the

truncation error seri es of the trapezoidal rule for step sizes h

and h

(Equation

(6.35)) using the extrapolation rule (Equation (6.38)). The numerical integral

approximations obtained using the trapezoidal rule are called the ﬁrst levels of

extrapolation. The Oh



approximation obtained using Equation (6.38) is called

the second level of extrapolation, where h ¼ h

Suppose we have two Oh



(level 2) integral approximations obtained for two

different step sizes. Based on the scheme described above, we can combine the two

results to yield a more accurate value:

ðÞþch

 Ih

ðÞþch

Eliminating c, we obtain the following expression:



ðÞ

ðÞIh

ðÞ

1

;

which simpliﬁes to



ðÞ

ðÞ (6:39)

when h

¼ h

=2. The error associated with Equation 6.39 is Oh



. Equation (6.39)

gives us a third level of extrapolation.

If k specifies the level of extrapolation, a generalized Richardson’s extrapolation formula to obtain

a numerical integral estimate of Oh

2kþ2



from two numerical estimates of Oh



, such that one

estimate of Oh



is obtained using twice the number of subintervals as that used for the other estimate

of Oh



,is

kþ1

h=2

ðÞ

 I

ðÞ

 1

: (6:40)

Note that Equation (6.40) applies only if the error term can be expressed as a series of

even powers of h. If the error term is given by

E ¼ c

þ c

þ

then the extrapolation form ula becomes

kþ1

h=2ðÞI

hðÞ

kþ1

 1

;

where level k = 1 corresponds to h

as the leading order of the truncation error.

Richardson’s extrapolation can be applied to integral approximations as well as

to ﬁnite difference (differentiation) app roximations. When this extrapolation tech-

nique is applied to numerical integration repeatedly to improve the accuracy of each

successive level of approximation, the scheme is called Romberg integration. The

goal of Romberg integration is to achieve a remarkably accurat e solution in a few

steps using the averaging formula given by Equation (6.40).

To perform Romberg integration, one begins by obtaining several rough

approximations to the integral whose value is sought, using the composite trapezoi-

dal rule. The numerical formula is calculated for several different step sizes equal to

ðb  aÞ=2

j1

, where j =1,2, ..., m,andm is the maximum level of integration

389

6.4 Richardson’s extrapolation and Romberg integration

(corresponding to an error  Oh



) desired; m can be any integral value  1. Let

j;k

denote the Romberg integral approximation at level k and with step size

ðb  aÞ=2

j1

. Initially, m integral approximations R

j;1

are generated using

Equation (6.22) . They are entered into a table whose columns represent the level

of integration (or order of magnitude of the error) (see Table 6.3). The rows

represent the step size used to compute the integral. The trapezoidal rule is used to

obtain all entries in the ﬁrst co lumn.

Using Equation (6.40), we can generate the entries in the second, third, ...,and

mth column. We rewrite Equation (6.40) to make it suitable for Romberg integration:

j;k



k1

j;k1

 R

j1;k1

k1

 1

: (6:41)

In order to reduce round-off error caused by subtraction of two numbers of dispa-

rate magnitudes, Equation (6.41) can be rearranged as follows:

j;k

 R

j;k1

 R

j1;k1

k1

 1

: (6:42)

Table 6.3 illustrates the tabulation of approximations generated during Romberg

integration for up to ﬁve levels of integration. Note that the function should be

differentiable many times over the integral to ensure quick convergence of Romberg

integration. If singularities in the derivatives arise at one or more points in the

interval, convergence rate deteriorates.

A MATLAB program to perform Romberg integration is listed in Program 6.5.

The function output is a matrix whose elements are the approximations R

j;k

MATLAB program 6.5

function R = Romberg_integration(integrandfunc, a, b, maxlevel)

% This function uses Romberg integration to calculate an integral when

% the integrand function is available in analytical form.

% Input variables

% integrandfunc : function that calculates the integrand

% a : lower limit of integration

% b : upper limit of integration

% maxlevel : maximum level of integration

Table 6.3. The Romberg integration table

Level of integration; order of magnitude of truncation error

k ¼ 1; Oh



k ¼ 2; Oh



k ¼ 3; Oh



k ¼ 4; Oh



k ¼ 5; Oh



Step size

j ¼ 1 R

1;1

j ¼ 2 R

2;1

2;2

j ¼ 3 R

3;1

3;2

3;3

j ¼ 4 R

4;1

4;2

4;3

4;4

j ¼ 5 R

5;1

5;2

5;3

5;4

5;5

The step size in any row is equal to ðb  aÞ=2

j1

390

Numerical quadrature

% Output variables

% I : value of integral

% Initializing variables

R(1:maxlevel,1:maxlevel) = 0;

j = [1:maxlevel];

n = 2.^(j-1); % number of subintervals vector

% Generating the ﬁrst column of approximations using trapezoidal rule

forl=1:maxlevel

R(l, 1) = trapezoidal_rule(integrandfunc, a, b, n(l));

end

% Generating approximations for columns 2 to maxlevel

fork=2:maxlevel

for l = k : maxlevel

R(l, k) = R(l, k - 1) + (R(l, k - 1) - R(l - 1, k - 1))/(4^(k–1) - 1);

end

In the current coding scheme, the function values at all 2

j1

þ 1 nodes are calculated

each time the trapezoidal rule is used to generate an approximation corresponding to

step size ðb  aÞ=2

j1

. The efﬁciency of the integration scheme can be improved by

recycling the function values evaluated at 2

j1

þ 1 nodes performed for a larger step

size to calculate the trapezoid integration result for a smaller step size (2

þ 1 nodes).

To do this, the trapezoidal formula Ih=2ðÞfor step size h/2 must be rewritten in terms

of the numerical result IhðÞfor step size h. (See Problem 6.9.)

Although the maximum number of integration levels is set as the stopping

criterion, one can also use a tolerance speciﬁcation to decide how many level s of

integration should be calculated. The tolerance criterion can be set based on the

relative error of two consecutive solutions in the last row of Table 6.3 as follows:

j;k

 R

j;k1

j;k

 Tol:

Problem 6.10 is concerned with developing a MATLAB routine to perform

Romberg integration to meet a user-speciﬁed tolerance.

6.5 Gaussian quadrature

Gaussian quadrature is a powerful numerical integration scheme that, like the

Newton–Cotes rules, uses a polynomial interpolant to approximate the behavior

of the integrand function within the limits of integration. The distinguishing feature

of the Newton–Cotes equations for integration is that the function evaluations are

performed at equally spaced points in the interval. In other words, the n + 1 node

points used to construct the polynomial interpolant of degree n are uniformly

distributed in the interval. The convenience of a single step size h greatly simpliﬁes

the weighted summation formulas, especially for composite integration rules, and

makes the Newton–Cotes formulas well suited to integrate tabular data. A Newton–

Cotes formula derived using a polynomial interpolant of degree n has a precision

equal to (1) n,ifn is odd, or (2) n +1,ifn is even.

391

6.5 Gaussian quadrature

It is possible to increa se the precision of a quadrature formula beyond n or n +1,

even when using an nth-degree polynomial interpolant to approximate the integrand

function. This can be done by optimizing the location of the n + 1 nodes between the

interval limits. By carefully choosing the location of the nodes, it is possible to

construct the “best” interpolating polynomial of degree n that approximates the

integrand function with the least error. Gaussian quadrature uses a polynomial of

degree n to approximate the integrand function and achieves a precision of 2n +1,

the highest precision attainable. In other words, Gaussian quadrature produces the

exact value of the integral of any polynomial function up to a degree of 2n + 1, using

a polynomial interpolant of a much smaller degree equal to n.

Like the Newton–Cotes formulas, the Gaussian quadrature formulas are

weighted summations of the integrand function evaluated at n + 1 unique points

within the interval:

fxðÞdx 

i¼0

ðÞ:

Box 6.3B IV drip

Romberg integration is used to integrate

t ¼

α þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ 8gðz þ LÞ



dz;

where

α ¼ 64Lμ=d

ρ,

length of tubing L = 91.44 cm,

viscosity μ = 0.01 Poise,

density ρ = 1 g/cm

diameter of tube d = 0.1 cm, and

radius of bag R = 10 cm.

We choose to perform Romberg integration for up to a maximum of four levels:

format long

Romberg_integration(‘IVdrip’,5, 50, 4)

0.58901064501874 6 0 0 0

0.57853989924056 9 0.575049650647843 0 0

0.57585132186699 2 0.574955129409132 0.574948827993218 0

0.57517429038364 3 0.574948613222527 0.574948178810086 0.574948168505592

The time taken for 90% of the bag to empty is given by

t ¼

0:5749482ðÞ;

which is equal to 45 996 seconds or 12.78 hours. Note the rapid convergence of the solution in the

second–fourth columns in the integration table above. To obtain the same level of accuracy using the

composite trapezoidal rule, one would need to use more than 2000 subintervals or steps! In Romberg

integration performed here, the maximum number of subintervals used is eight.

392

Numerical quadrature

However, the nodes x

are not evenly spaced within the interval. The weights w

can

be calculated by integrating the Lagrange polynomials once the positions of the

nodes are determined. How does one determine the optimal location of the n +1

nodes so that the highest degree of precision is obtained?

First, let’s look at the disadvantage of using an even spacing of the nodes

within the interval. Uniform node spacing can result in sizeable errors in the

numerical solution. When nodes are positioned at equal intervals, the i nterpo-

lating polynomial that is constructed from the function values at these nodes is

more likely to be a poor representation of the t rue function. Consider using the

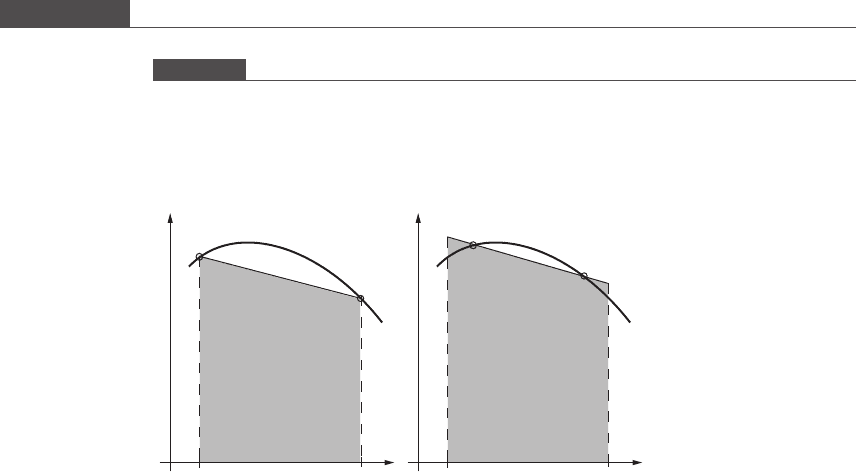
trapezoidal rule to integrate the downward concave function shown i n

Figure 6.14. If the function’s value at the midpoint of the interval is located

far above its endpoint values, the straight-line function that passes through the

interval endpoints will grossly underestimate the value of the integral

(Figure 6.14(a)). However, if the two node points are positioned inside the

interval at a suitable distance from the integration limits, then the line function

will overestimate the integral in some r egions of the interval and underestimate

the integral in other regions, allowing the errors to largely cancel each other

(Figure 6.14(b)). The overall error is much smaller.

Since an optimal choice of node positions is expected to impr ove the accuracy of

the solut ion, intuitively we expect Gaussian quadrature to have greater precision

than a Newton–Cotes formula with the same degree of the polynomial interpolant.

If the step size is not predetermined (the step size is predetermined for Newton–Cotes

rules to allow for equal subinterval widths), the quadrature formula of Equation

(6.1) has 2n + 2 unknown parameters: n + 1 weights, w

,andn + 1 nodes, x

. With

the ad ditional n + 1 adjustable parameters of the quadrature formula, it is possible

to increase the precision by n + 1 degrees from n (typical of Newton–Cotes

formulas) to 2n +1.

In theory, we can co nstruct a set of 2n + 2 nonlinear equations by equating the

weighted summation formula to the exact value of the integral of the ﬁrst 2n +2

positive integer power functions (1; x; x

; x

; ...; x

2nþ1

) with integration limits

Figure 6.14

Accuracy in numerical quadrature increases when the nodes are strategically positioned within the interval. This is

shown here for a straight-line function that is used to approximate a downward concave function. (a) The two nodes

are placed at the interval endpoints according to the trapezoidal rule. (b) The two nodes are placed at some specified

distance from the integration limits according to the Gaussian quadrature rule.

y = f(x)

= p(x)

y = f(x)

= p(x)

(a)

(b)

393

6.5 Gaussian quadrature

½1; 1. On solving this set of equations, we can determine the values of the 2n +2

parameters of the summation formula that will produce the exact result for the

integral of any positive integer power function up to a maximum degree of 2n +1.A

(2n + 1)th-degree polynomial is simply a linear combination of positive integer

power functions of degrees from 0 to 2n + 1. The resulting (n + 1)-point quadrature

formula will be exact for all polynomials up to the (2n + 1)th degree. We demon-

strate this method to ﬁnd the parameters of the two-point Gaussian quadrature

formula for a straight-line approximation (ﬁrst-degree polynomial interpolant) of

the integran d function.

A Gaussian quadrature rule that uses an interpolating polynomial of degree n =1

has a degree of precision equal to 2n + 1 = 3. In other words, the integral of a cubic

function c

þ c

x þ c

can be exactly calculated using a two-point

Gaussian quadrature rule. The integration interval is chosen as ½1; 1 ,soasto

coincide with the interval within which orthogonal polynomials are deﬁned. These

are an important set of polyno mials and will be introduced later in this section. Since

1

fxðÞdx ¼

1

þ c

x þ c



¼ c

1

dx þ c

1

dx þ c

1

xdx þ c

1

dx;

the two-point quadrature formula must be exact for a constant function, linear

function, quadratic function, and cubic function, i.e. for fxðÞ¼1; x; x

; x

.We

simply need to equate the exact value of each integral with the weighted summation

formula. There are two nodes, x

and x

, that both lie in the interior of the interval.

We have four equations of the form

1

fxðÞdx ¼ w

ðÞþw

ðÞ;

where fxðÞ¼1 ; x; x

; or x

. Writing out the four equations, we have

fxðÞ¼1: w

þ w

¼ 2;

fxðÞ¼x: w

þ w

¼ 0;

fxðÞ¼x

: w

þ w

¼ 2=3;

fxðÞ¼x

: w

þ w

¼ 0:

Solving the second and fourth equations simultaneously, we obtain x

¼ x

. Since

the two nodes must be distinct, we obtain the relation x

¼x

. Substituting this

relationship between the two nodes back into the second equation, we get w

¼ w

The ﬁrst equation yields

¼ w

¼ 1;

and the third equation yields

¼

ﬃﬃﬃ

; x

ﬃﬃﬃ

The two-point Gaussian quadrature formula is

I  f 

ﬃﬃﬃ



þ f

ﬃﬃﬃ



; (6:43)

394

Numerical quadrature

which has a degree of precision equal to 3. It is a linear combination of two function

values obtained at two nodes equidistant from the midpoint of the interv al.

However, the two nodes lie slightly closer to the endpoints of their respective sign

than to the midpoint of the interval.

Equation (6.43) applies only to the integration limits −1 and 1. We will need to

modify it so that it can apply to any integ ration interval. Let x be the variable of

integration that lies between the limits of closed integration a and b. If we deﬁne a

new integration variable y such that y ¼ x ða þ bÞ=2, the integral over the interval

½a; b becomes

fxðÞdx ¼

ðbaÞ=2

ðbaÞ=2

a þ b

þ y



dy:

The midpoint of the new integration interval is zero. Now divide the integration

variable y by half of the interval width ðb  aÞ=2 to deﬁne a new integration variable

z ¼ 2y=ðb  aÞ¼2x=ðb  aÞða þ bÞ=ðb  aÞ. The limits of integration for the

variable z are −1 and 1. A linear trans formation of the new variable of integration

z recovers x:

x ¼

b  a

z þ

a þ b

Differentiating the above equation we have dx ¼ðb  aÞ=2 dz. The integral can now

be written with the integration limits −1 and 1:

I ¼

fxðÞdx ¼

b  a

1

b  a

z þ

a þ b



dz: (6:44)

The Gaussian quadrature rule for any integration interval ½a; b is

fxðÞdx ¼

b  a

1

b  a

z þ

a þ b



dz 

b  a

i¼0

b  a

a þ b



;

(6:45)

where z

are the n + 1 Gaussian nodes and w

are the n + 1 Gaussian weights.

The two-point Gaussian quadrature rule can now be applied to any integration

interval using Equation (6.45):

fxðÞdx 

b  a



ﬃﬃﬃ



a þ b



þ f

b  a

ﬃﬃﬃ



a þ b



(6:46)

Gaussian quadrature formulas given by Equations (6.45) and (6.46) are straightfor-

ward and easy to evaluate once the nodes and weights are known. Conversely,

calculation of the optimal node points and weights is not as straightforward. One

method of ﬁnding the optimal node points and co rresponding weights is by solving a

system of 2n + 2 nonlinear equations, as discussed earlier. However, this method is

not practical for higher precision quadrature rules since a solution to a large set of

nonlinear equations is difﬁcult to obtain. Instead, we ap proximate the function fðxÞ

with a Lagrange interpolation polynomial just as we had done to derive the Newton–

Cotes formulas in Section 6.3:

395

6.5 Gaussian quadrature

fxðÞdx 

i¼0

ðÞ∏

j¼0;j6¼i

x  x



 x



i¼0

ðÞ

∏

j¼0; j6¼i

x  x



 x



b  a

i¼0

ðÞ

1

∏

j¼0; j6¼i

z  z



 z



b  a

i¼0

ðÞ;

where

1

∏

j¼0; j6¼i

z  z



 z



dz (6:47)

and

x ¼

b  a

z þ

a þ b

To calculate the weights we must ﬁrst determine the location of the nodes.

The n + 1 node positions are calculated by enforcing that the truncation error

of the quadrature formula be exactly zero when integrating a polynomial

function of degree ≤ 2n + 1. The roots of the (n + 1)th-degree Legendre poly-

nomial deﬁne the n + 1 nodes of the Gaussian quadrature formula at which

fðxÞ evaluations are required (see Appendix B for the derivation). Legendre

polynomials are a class of orthogonal polynomials. This particular quadrature

method is called Gauss–Legendre quadrature. Other Gaussian quadrature meth-

ods have also been developed, but are not discussed i n this book.

The Legendre polynomials are

zðÞ¼1;

zðÞ¼z;

zðÞ¼

 1



;

zðÞ¼

 3z



;

zðÞ¼

 1



: (6:48)

Equation (6.48) is called the Rodrigues’ formula.

396

Numerical quadrature