King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

constraining value of y will lie either at the initial point or the ﬁnal point of the

integration interval. If the constraint provided is at the ﬁnal or end time t

, i.e.

ðÞ¼y

, then the ODE integration proceeds backward in time from t

to zero,

rather than forward in time. However, this problem is mathematically equivalent to

an IVP with the constraint provided at t =0.

To perform numerical ODE integration, the interval ½0; t

of integration must be

divided into N subint ervals of equal size. The size of one subinterval is called the step

size, and is represented by h. We will co nsider ODE integration with varying step

sizes in Section 7.4. Thus, the interval is discretized into N ¼ t

=h þ 1 points, and the

differential equation is solved only at those points . The ODE is integrated using a

forward-marching numerical scheme. The solution yðtÞ is calculated at the endpoint

of each subinterval, i.e. at t ¼ t

; t

; ...; t

, in a step-wise fashion. The numerical

solution of y is therefore not continuous, but, with a small enough step size, the

solution will be sufﬁciently descriptive and reasonably accurate.

7.2.1 Euler’s forward method

In Euler’s explicit method, h is chosen to be small enough such that the slope of the

function yðtÞ within any subinterval remains approximately constant. Using the

ﬁrst-order forward ﬁnite difference formula (see Section 1.6.3 for a discus sion on

ﬁnite difference form ulas and numerical differentiation) to approximate a ﬁrst-order

derivative, we can rewrite dy=dt within the subinterval ½t

; t

in terms of a numerical

derivative:



¼0

¼ fð0; y

Þ

 yð0Þ

 0

 y

The above equation is rearranged to obtain

¼ y

þ hfð0; y

Þ:

Here, we have converted a differential equation into a difference equation that allows

us to calculate the value of y at time t

, using the slope at the previous point t

Because the forward ﬁnite difference is used to derive the difference equation, this

method is also commonly known as Euler’s forward method. Note that y

is not the

same as yt

ðÞ; y

is the approximate (or numerical) solution of y at t

. The exact or

true solution of the ODE at t

is denoted as yt

ðÞ. The difference equation is

inherently associated with a truncation error (called the local truncation error)

whose order of magnitude we will determine shortly.

Euler’s forward method assumes that the slope of the y trajectory is constant

within the subinterval and is equal to the initial slope. If the step size is sufﬁciently

small and/or the slope changes slowly, then the assum ption is acceptable and the

error that is generated by the numerical approximation is small. If the trajectory

curves sharply within the subint erval, the constancy of slope assumption is invalid

and a large numerical error will be produced by this difference equation.

Because the values on the right-hand side of the above difference equation are

speciﬁed by the initial condition and are therefore known to us, the solution technique

is said to be explicit,allowingy

to be calculated directly. Once y

is calculated, we can

obtain the approximate solution y

for y at t

, which is calculated as

¼ y

þ hf t

; y

ðÞ:

417

7.2 Euler’s methods

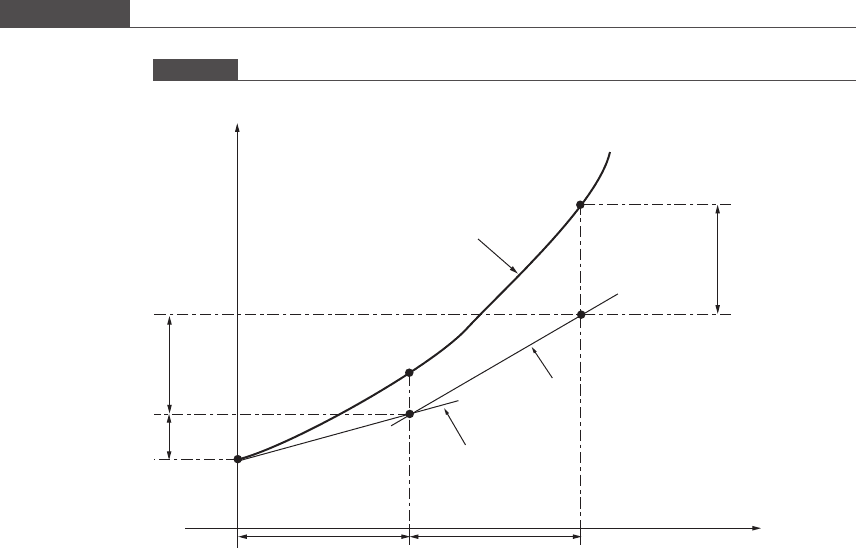
Since y

is the approximate solution for yt

ðÞ, errors involved in estimating yt

ðÞwill

be included in the estimate for yt

ðÞ. Thus, in addition to the inherent truncation

error at the present step associated wi th using the numerical derivative approxima-

tion, we also observe a propagation of previous errors as we march forward from

t =0 to t = t

. Figure 7.1 illustrates the step-wise marching technique used by

Euler’s method to ﬁnd the approximate solution, at the ﬁrst two time points of the

discretized interval.

We can generalize the above equation for any subinterval ½t

; t

kþ1

, where k =0,

1, 2, 3, ..., N − 1 and t

kþ1

 t

¼ h:

kþ1

¼ y

þ hf t

; y

ðÞ: (7:15)

Note that, while the true solution yðtÞ is continuous, the numerical solution,

; y

; ...; y

; y

kþ1

; ...; y

, is discrete.

Local and global truncation errors

Let us now assess the magnitude of the truncation error involved with Euler’s

explicit method. There are two types of errors produced by an ODE numeri cal

integration scheme. The ﬁrst type of error is the local truncation error that is

generated at every step. The local truncation error generated in the ﬁrst step is

carried forward to the next step and thereby propagates through the numerical

solution to the ﬁnal step. As each step produces a new local truncation error, these

errors accumulate as the numerical calculation progresses from one iteration to the

next. The total error at any step, which is the sum of the local truncation error and

the propagated errors, is called the global truncation error.

Figure 7.1

Numerical integration of an ODE using Euler’s forward method.

)

slope = f(0, y

)

hf(0, y

)

slope = f(

, y

)

hf(

, y

)

Truncation error

y(t)

Exact solution

418

Numerical integration of ODEs

When we perform the ﬁrst step of the numerical ODE integration, the starting

value of y is know n exactly. We can express the exact solution at t ¼ t

in terms of the

solution at t

using the Taylor series (see Section 1.6 for a discussion on Taylor

series) as follows:

ðÞ¼yt

ðÞþy

ðÞh þ

ξðÞh

; ξ 2 t

; t

½:

The ﬁnal term on the right-hand side is the remainder term discussed in Section 1.6.

Here, the remainder term is the sum total of all the terms in the inﬁnite series except

for the ﬁrst two. The ﬁrst two terms on the right-hand side of the equation are

already known:

ðÞ¼y

þ hfð0; y

Þþ

ξðÞh

ðÞ¼y

ξðÞh

Therefore,

ðÞy

ξðÞh

If y

ðtÞ

 M for 0  t  t

, then

ðÞy



 Oh



: (7:16)

The order of magnitude of the local truncation error associated with the numerical

solution of y at t

is h

. For the ﬁrst step, the local truncation error is equal to the

global truncation error. The local truncation error generated at each step is Oh



For the second step, we express yt

ðÞ

in terms of the exact solution at the previous

step,

ðÞ¼yt

ðÞþhf t

; yt

ðÞðÞþ

ξðÞh

; ξ 2 t

; t

½:

Since yt

ðÞis unknown, we must use y

in its place. The truncation error associated

with the numerical solution for yt

ðÞis equal to the sum of the local truncation error,

ξðÞh

=2!, generated at this step, the local truncation error associated with y

, and

the error in calculating the slope at t

, i.e. ft

; yt

ðÞðÞft

; y

ðÞ. At the (k + 1)th step,

the true solution yt

kþ1

ðÞis expressed as the sum of terms involving yt

ðÞ:

kþ1

ðÞ¼yt

ðÞþhf t

; yt

ðÞðÞþ

ξðÞh

; ξ 2 t

; t

kþ1

½: (7:17)

Subtracting Equation (7.15) from Equation (7.17), we obtain the global truncation

error in the numerical solution at t

kþ1

ðÞy

kþ1

¼ yt

ðÞy

þ hft

; yt

ðÞðÞft

; y

ðÞðÞþ

ξðÞh

: (7 :18)

We use the mean value theorem to simplify the above equation. If fðyÞ is continuous

and differentiable within the interval y 2½a; b, then the mean value theorem states

that

419

7.2 Euler’s methods

fbðÞfðaÞ

b  a

dfðyÞ



y¼c

; (7:19)

where c is a number within the interval ½a; b. In other words, the slope of the line

joining the endpoints of the interval a; faðÞðÞand b; fbðÞðÞis equal to the derivative of

fðyÞ at the point c , which lies within the same interval.

Applying the mean value theorem (Equation (7.19))toEquation (7.18), we obtain

kþ1

ðÞy

kþ1

¼ yt

ðÞy

þ h

∂ft

; cðÞ

∂y

ðÞy

ðÞþ

ξðÞh

kþ1

ðÞy

kþ1

¼ 1 þ h

∂ft

; cðÞ

∂y



ðÞy

ðÞþ

ξðÞh

If y

ðtÞ

 M for 0  t  t

, ∂ft; yðÞ=∂y

 C for 0  t  t

and a  y  b (also

called the Lipschitz criterion), then

kþ1

ðÞy

kþ1

 1 þ hCðÞyt

ðÞy

ðÞþ

: (7:20)

Now, yt

ðÞy

is the global truncation error of the numerical solution at t

. Since

Equation (7.20) is valid for k  1, we can write

ðÞy

 1 þ hCðÞyt

k1

ðÞy

k1

ðÞþ

Substituting the above expression into Equation (7.19), we get

kþ1

ðÞy

kþ1

 1 þ hCðÞ1 þ hCðÞyt

k1

ðÞy

k1

ðÞþ



kþ1

ðÞy

kþ1

 1 þ hCðÞ

k1

ðÞy

k1

ðÞþ1 þ 1 þ hCðÞðÞ

Performing the substitutions for the global truncation error at t

k1

; t

k2

; ...; t

recursively, we obtain

kþ1

ðÞy

kþ1

 1 þ hCðÞ

ðÞy

ðÞ

þ 1 þ 1 þ hCðÞþ1 þ hCðÞ

þþ 1 þ hCðÞ

k1



;

ðÞy

is given by Equation (7.16) and only involves the local truncation error.

The equation above becomes

kþ1

ðÞy

kþ1

 1 þ 1 þ hCðÞþ1 þ hCðÞ

þþ 1 þ hCðÞ

k1

þ 1 þ hCðÞ



The sum of the geometric series 1 þ r þ r

þþr

is ðr

nþ1

 1Þ=ðr  1Þ, and we use

this result to simplify the above to

C is some constant value and should not be confused with c, which is a point between a and b on the

y-axis.

420

Numerical integration of ODEs

kþ1

ðÞy

kþ1



1 þ hCðÞ

kþ1

1

1 þ hCðÞ1



: (7:21)

Using the Taylor series, we can expand e

as follows:

¼ 1 þ hC þ

hCðÞ

þ:

Therefore,

1 þ hC:

Substituting the above into 7.21,

kþ1

ðÞy

kþ1

hðkþ1ÞC

 1



If k þ 1 ¼ N, then hN ¼ t

, and the ﬁnal result for the global truncation error at t

ðÞy

 1





 OhðÞ: (7:22)

The most important result of this derivation is that the global truncation error of

Euler’s forward method is OhðÞ. Euler’s forward method is called a ﬁrst-order method.

Note that the order of magnitude of the global truncation error is one order less than

that of the local truncation error. In fact, for any numerical ODE integration

technique, the global truncation error is one order of magnitude less than the local

truncation error for that method.

Example 7.1

We use Euler’s method to solve the linear first-order ODE

¼ t  y; y 0ðÞ¼1: (7:23)

The exact solution of Equation (7.23) is y ¼ t  1 þ 2e

t

, which we will use to compare with the

numerical solution.

To solve this ODE, we create two m-files. The first is a general purpose function file named

eulerforwardmethod.m that solves any first-order ODE using Euler’sexplicitmethod.Thesecondisa

function file named simplelinearODE.m that evaluates fðt; yÞ, i.e. the right-hand side of the ODE

specified in the problem statement. The name of the second function file is supplied to the first function.

The function feval (see Chapter 5 for usage) is used to pass the values of t and y to

simplelinearODE.m and calculate ft; yðÞat the point t; yðÞ.

MATLAB program 7.1

function [t, y] = eulerforwardmethod(odefunc, tf, y0, h)

% Euler’s forward method is used to solve a ﬁrst-order ODE

% Input variables

% odefunc : name of the function that calculates f(t, y)

%tf:ﬁnal time or size of interval

% y0 : y(0)

% h : step size

% Output variables

421

7.2 Euler’s methods

t = [0:h:tf]; % vector of time points

y = zeros(size(t)); % dependent variable vector

y(1) = y0; % indexing of vector elements begins with 1 in MATLAB

% Euler’s forward method for solving a ﬁrst-order ODE

for k = 1:length(t)-1

y(k+1) = y(k)+ h*feval(odefunc, t(k), y(k));

end

MATLAB program 7.2

function f = simplelinearODE(t, y)

% Evaluate slope f(t,y) =t-y

f=t-y;

MATLAB program 7.1 can be called from the command line

[t, y] = eulerforwardmethod(‘simplelinearODE’, 3, 1, 0.5)

Figure 7.2 shows the trajectory of y obtained by the numerical solution with step sizes h = 0.5, 0.2, and

0.1, and compares this with the exact solution.

We see from the figure that the accuracy of the numerical scheme increases with decreasing h. The

maximum global truncation error for each trajectory is shown in Table 7.1.

Figure 7.2

Numerical solution of Equation (7.23) using Euler’s forward method for three different step sizes.

0 0.5 1 1.5 2 2.5 3

0.5

1.5

Exact y(t)

h = 0.5

h = 0.2

h = 0.1

Table 7.1. Change in maximum global truncation error with step size

Numerical solution Step size Maximum global truncation error

1 0.5 0.2358

2 0.2 0.0804

3 0.1 0.0384

422

Numerical integration of ODEs

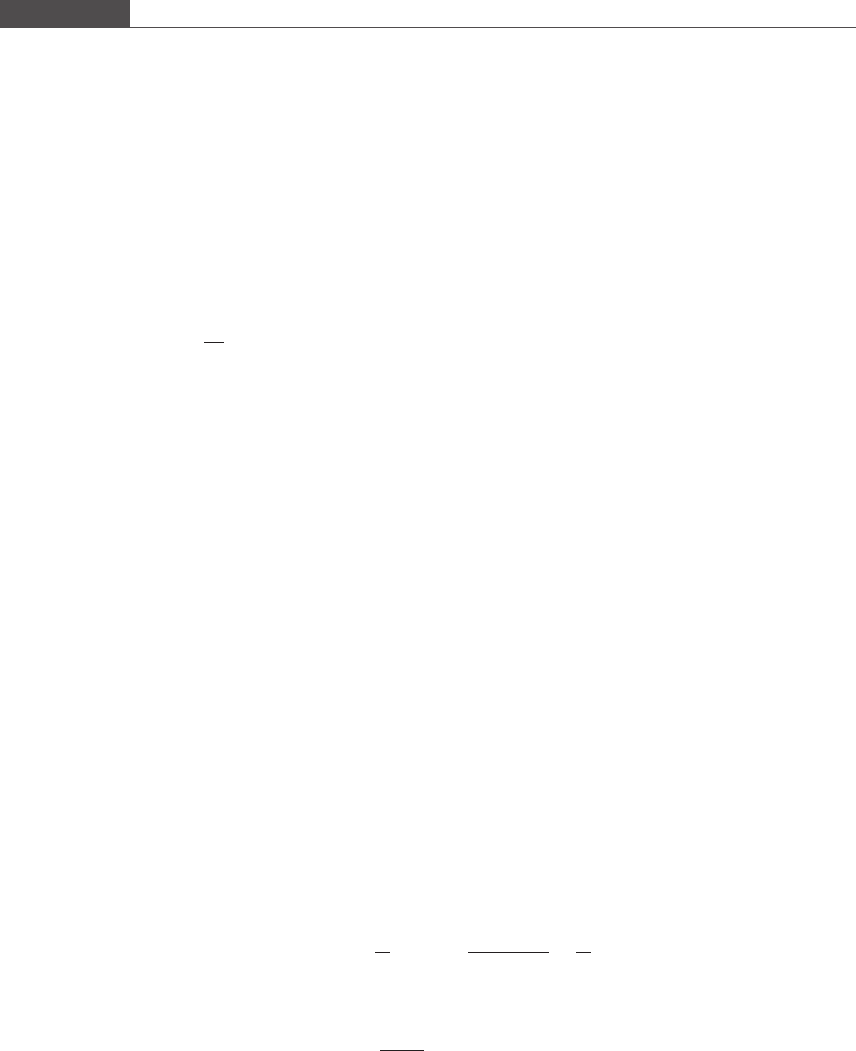
For a decrease in step size of 0:2=0:5 ¼ 0:4, the corresponding decrease in maximum global

truncation error is 0:0804=0:2358 ¼ 0:341. The global error is reduced by the same order of

magnitude as the step size. Similarly, a decrease in step size of 0:1=0:2 ¼ 0:5 produces a decrease in

maximum global truncation error of 0:0384=0:0804 ¼ 0:478. The maximum truncation error reduces

proportionately with a decrease in h. Thus, the error convergence to zero is observed to be O(h), as

predicted by Equation (7.22). Therefore, if h is cut by half, the total truncation error will also be reduced by

approximately half.

Stability issues

Let us consider the simple ﬁrst-order ODE

¼ λy; y 0ðÞ¼α: (7:24)

The exact solution of Equation (7.24) is y ¼ αe

λt

. We can use the exact solution to

benchmark the accuracy of Euler’s forward method and ch aracterize the limitations

of this method. The time interval over which the ODE is integrate d is divided into N

equally spaced time points. The uniform step size is h.

At t ¼ t

, the numerical solution is

¼ y 0ðÞþhλy 0ðÞ¼α þ hλα ¼ α 1 þ λhðÞ:

At t ¼ t

¼ y

þ hλy

¼ 1 þ λhðÞy

¼ α 1 þ λhðÞ

At t ¼ t

kþ1

¼ 1 þ λhðÞy

¼ α 1 þ λhðÞ

kþ1

And at t ¼ t

¼ α 1 þ λhðÞ

: (7:25)

Fortunately, for this problem, we have arrived at a convenient expression for the

numerical solut ion of y at any time t. We use this simple expression to illustrate a few

basic concepts about Euler’s method. If the step size h ! 0, the number of incre-

ments N ! ∞.

The expression in Equation (7.25) can be expanded using the binomial theorem as

follows:

1 þ λhðÞ

¼ 1

þ Nλ

 1

N1

NN 1ðÞ



N2

þ;

where h ¼ t

=N. When N ! ∞, h ! 0, and λh  1: The above expression becomes

1 þ λhðÞ

∞

 1 þ λt

λt

ðÞ

þ¼e

λt

Therefore,

¼ αe

λt

When h ! 0, the numerical solution approaches the exact solution. This example

shows that for a very small step size, Euler’s method will converge upon the true

solution. For very small h, a large number of steps must be taken before the end of

the interval is reached. A very large value of N has several disadvantages: (1) the

423

7.2 Euler’s methods

method becomes computationally expensive in terms of the number of required

operations; (2) round-off errors can dominate the total error and any improvement

in accuracy is lost; (3) round-off errors will accumulate and become relatively large

because now many, many steps are involved. This will corrupt the ﬁnal solution at

t ¼ t

What happens when h is not small enough? Let’s ﬁrst take a closer look at the

exact solution. If λ

0, the true solution blows up at large times and y ! ∞. We are

not interested in the unstable problem. We consider only those situations in which

0. For these values of λ the solution decays with time to zero. Examples of

physical situations in which this equation applies are radioactive decay, drug elim-

ination by the kidneys, and ﬁrst-order (irreversible) consumption of a chemical

reactant.

In a ﬁrst-order decay problem,

¼λy; λ

0: yð0Þ

According to the exact solution, it is always the case that yt

ðÞ

yðt

Þ, where t

The numerical solution of this ODE problem is y

kþ1

¼ 1  λhðÞy

.When

1  λh

1, then we will always have y

kþ1

. To achieve a decaying solution, h

must be constrained to the range 1

1  λh

1or0

2=λ. Note that h is always

positive in a forward-marching scheme, so the condition that assures a decaying

numerical solution is h

2=λ.If0

1=λ, then the decay is monotonic. If

1=λ

2=λ, an oscillatory decay is observed. What happens when h ¼ 1=λ?If

h ¼ 2=λ, then the numerical solution does not decay but instead oscillates from α

to α at every time step.

When h  2=λ, the numerical solution is bounded and the numerical solution is said

to be stable over this range of step size values. The accuracy of the solution will depend

on the size of h.Whenh

2=λ, the numerical solution diverges with time with sign

reversal at each step and tends towards inﬁnity. The solution blows up because the

errors grow (as opposed to decay) exponentially and cause the solution to blow up. For

this range of h values, the numerical solution is unstable. The magnitude of λ deﬁnes the

upper bound for the step size. A large λ requires a very small h to ensure stability of the

numerical technique. However, if h is too small, then the limits of numerical precision

may be reached and round-off error will preclude any improvement in accuracy.

The stability of numerical integration is determined by the ODE to be solved, the

step size,

and the numerical integration scheme. We explore the stability limits of

Euler’s method by looking at how the error accumulates with each step. Equation

(7.20) express es the global truncation error at t

kþ1

in terms of the error at t

kþ1

ðÞy

kþ1

 1 þ h

∂f

∂y



ðÞy

ðÞþ

: (7:20)

Note that the global error at t

, which is given by yt

ðÞy

, is multiplied by an

ampliﬁcation factor, which for Euler’s forward method is 1 þ hð∂f=∂yÞ.Ifð∂f=∂y Þ is

positive, then 1 þ h ð∂f=∂yÞ

1, and the global error will be ampliﬁed regardless of

the step size. Even if the exact solution is bounded, the numerical solution may

accumulate large errors along the path of integrati on. If ð∂f=∂yÞ is negative and h is

chosen such that 1  1 þ h ð∂f=∂yÞ

1, then the error remains bounded for all

times within the time interval. However, if ð∂f=∂yÞ is very negative, then ð∂f=∂yÞjj

is large. If h is not small enou gh, then 1 þ hð∂f=∂yÞ

 1orhð∂f=∂yÞ

 2. The

errors

will be magniﬁed at each step, and the numerical method is rendered unstable.

424

Numerical integration of ODEs

ODEs for which df t; yðÞ=dy 1 over some of the time interval are called stiff

equations. Section 7.6 discusses this topic in detail.

Coupled ODEs

When two or more ﬁrst-order ODEs are coup led, the set of differential equations are

solved simultaneously as a system of ﬁrst-order ODEs as follows:

¼ f

t; y

; y

; ...; y

ðÞ

¼ f

t; y

; y

; ...; y

ðÞ

¼ f

t; y

; y

; ...; y

ðÞ:

A system of ODEs can be represented compactly using vector notation. If

y ¼½y

; y

; ...; y

 and f ¼½f

; f

; ...; f

, then we can write

¼ f t; yðÞ; y 0ðÞ¼y

; (7:26)

where the bold notation represents a vector (lower-case) or matrix (upper-case)

(notation to distinguish vectors from scalars is discussed in Section 2.1) as opposed

to a scalar.

A set of ODEs can be solved using Euler’s explicit formula. For a three-variable

system,

¼ f

t; y

; y

ðÞ; y

0ðÞ¼y

1;0

;

¼ f

t; y

; y

ðÞ; y

0ðÞ¼y

2;0

;

the numerical formula prescribed by Euler’s method is

1;kþ1

¼ y

1;k

þ hf

; y

1;k

; y

2;k



;

2;kþ1

¼ y

2;k

þ hf

; y

1;k

; y

2;k



The ﬁrst subscript on y identiﬁes the dependent variable and the second subscript

denotes the time point. The same forward-marching scheme is performed. At each

time step, t

kþ1

, y

1;kþ1

,andy

2;kþ1

are calculated, and the iteration proceeds to the next

time step. To solve a higher-order ordinary differential equation, or a system of

ODEs that contains at least one higher-order differential equation, we need to

convert the problem to a mathematically equivalent system of coupled, ﬁrst-order

ODEs.

Example 7.2

A spherical cell or particle of radius a and uniform density ρ

, is falling under gravity in a liquid of density ρ

and viscosity μ . The motion of the sphere, when wall effects are minimal, can be described by the equation

πa

þ 6μπav 

πa

ðρ

 ρ

Þg ¼ 0;

425

7.2 Euler’s methods

or, using v ¼ dz=dt,

πa

þ 6μπa



πa

ðρ

 ρ

Þg ¼ 0;

with initial boundary conditions

z 0ðÞ¼0; v ¼

¼ 0;

where z is the displacement distance of the sphere in the downward direction. Downward motion is along

the positive z direction. On the left-hand side of the equation, the first term describes the acceleration, the

second describes viscous drag, which is proportional to the sphere velocity, and the third is the force due

to gravity acting downwards from which the buoyancy force has been subtracted. Two initial conditions are

included to specify the problem completely. This initial value problem can be converted from a single

second-order ODE into a set of two coupled first-order ODEs.

Set y

¼ z and y

¼ dz=dt. Then,



ðρ

 ρ

g 

9μ

We now have two simultaneous first-order ODEs, each with a specified initial condition:

¼ y

; y

0ðÞ¼0; (7:27)

ðρ

 ρ

g 

9μ

; y

0ðÞ¼0: (7:28)

The constants are set to

a ¼ 10 μm; ρ

¼ 1:1g=cm

; ρ

¼ 1g=cm

; g ¼ 9:81 m=s

; μ ¼ 3:5cP:

We solve this system numerically using Euler’s explicit method. Program 7.1 was designed to solve only

one first-order ODE at a time. The function described in Program 7.1 can be generalized to solve a set of

coupled ODEs. This is done by vectorizing the numerical integration scheme to handle Equation (7.26). The

generalized function that operates on coupled first-order ODEs is named eulerforwardmethodvec-

torized. The variable y in the function file eulerforwardmethodvectorized.m is now a matrix with the row

number specifying the dependent variable and the columns tracking the progression of the variables’ values in

time. The function file, settlingsphere.m, evaluates the slope vector f.

MATLAB program 7.3

function [t, y] = eulerforwardmethodvectorized(odefunc, tf, y0, h)

% Euler’s forward method is used to solve coupled ﬁrst-order ODEs

% Input variables

% odefunc : name of the function that calculates f(t, y)

%tf:ﬁnal time or size of interval

% y0 : vector of initial conditions y(0)

% h : step size

% Other variables

n = length(y0); % number of dependent time-varying variables

% Output variables

t = [0:h:tf]; % vector of time points

426

Numerical integration of ODEs