King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

y = zeros(n, length(t)); % dependent variable vector

y(:,1) = y0; % initial condition at t = 0

% indexing of matrix elements begins with 1 in MATLAB

% Euler’s forward method for solving coupled ﬁrst-order ODEs

for k = 1:length(t)-1

y(:,k+1) = y(:,k)+ h*feval(odefunc, t(k), y(:,k));

end

MATLAB program 7.4

function f = settlingsphere(t, y)

% Evaluate slopes f(t,y) of coupled equations

a = 10e-4; % cm : radius of sphere

rhos = 1.1; % g/cm3 : density of sphere

rhof = 1; % g/cm3 : density of medium

g = 981; % cm/s2 : acceleration due to gravity

mu = 3.5e-2; % g/cm.s : viscosity

f = [y(2); (rhos - rhof)*g/rhos - (9/2)*mu*y(2)/(a^2)/rhos];

Equations (7.27) and (7.28) are solved by calling the eulerforwardmethodvectorized func-

tion from the MATLAB command line. We choose a step size of 0.0001 s:

[t, y] = eulerforwardmethodvectorized (‘settlingsphere’, 0.001,

[0; 0], 0.0001);

Plotting the numerically calculated displacement z and the velocity dz=dt with time (Figure 7.3), we

observe that the solution blows up. We know that physically this cannot occur. When the sphere falls from

rest through the viscous medium, the downward velocity increases monotonically from zero and

reaches a final settling velocity. At this point the acceleration reduces to zero. The numerical method is

unstable for this choice of step size since the solution grows without bound even though the exact

solution is bounded. You can calculate the terminal settling velocity by assuming steady state for the force

balance (acceleration term is zero).

Figure 7.3

Displacement and velocity trajectories for a sphere settling under gravity in Stokes flow. Euler’s explicit method exhibits

numerical instabilities for the chosen step size of h = 0.0001 s.

0 0.5 1

−2

× 10

t (ms)

z (μm)

0 0.5 1

−12

−10

−8

−6

−4

−2

× 10

t (ms)

v (μm/s)

427

7.2 Euler’s methods

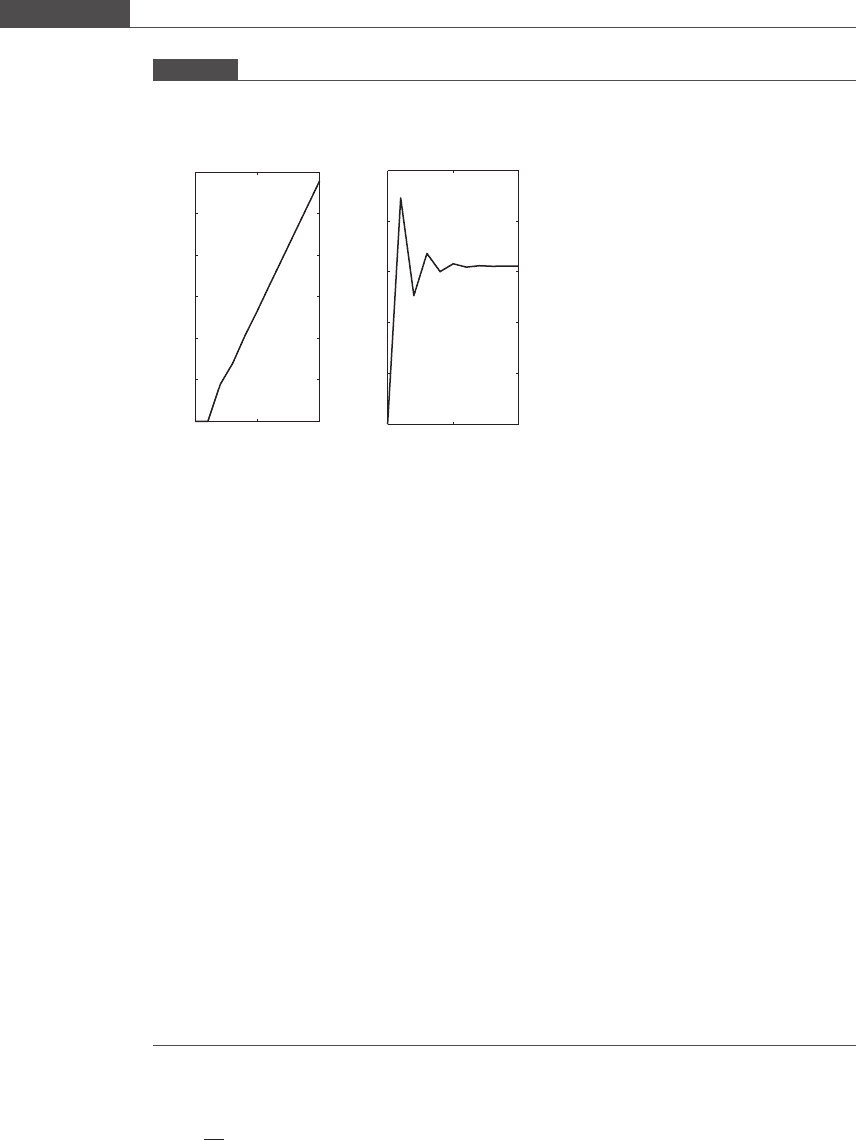
We reduce the step size by an order of magnitude to 0.00001 s:

[t, y] = eulerforwardmethodvectorized (‘settlingsphere’, 0.0001,

[0; 0], 0.00001);

and re-plotting the time-dependent displacement and velocity (Figure 7.4), we observe that the final

solution is bounded, but the velocity profile is unrealistic. The numerical method is stable for this choice of

step size, yet the solution is terribly inaccurate; the steps are too far apart to predict a physically realizable

situation.

Finally we choose a step size of 1 μ s. Calling the function once more:

[t, y] = eulerforwardmethodvectorized (‘settlingsphere’, 0.0001,

[0; 0], 0.000001);

we obtain a physically meaningful solution in which the settling velocity of the falling sphere monotonically

increases until it reaches the terminal velocity, after which it does not increase or decrease. Figure 7.5 is a

plot of the numerical solution of the coupled system using a step size of 1 μs.

Some differential equations are sensitive to step size, and require exceedingly small step sizes to

guarantee stability of the solution. Such equations are termed as stiff. Issues regarding stability of the

numerical technique and how best to tackle stiff problems are taken up in Section 7.6.

7.2.2 Euler’s backward method

For deriving Euler’s forward method, the forward ﬁnite difference formula was used

to approximate the ﬁrst derivative of y. To convert the differential problem

¼ ft; yðÞ; yt¼ 0ðÞ¼y

;

into a diff erence equation, this time we replace the derivative term by the backward

ﬁnite difference formula (Equation (1.23)). In the subinterval t

; t

kþ1

½; the deriva-

tive dy=dt at the time point t

kþ1

is approximated as

Figure 7.4

Displacement and velocity trajectories for a sphere settling under gravity in Stokes flow. Euler’s explicit method is stable

but the velocity trajectory is not physically meaningful for the chosen step size of h =10μs.

0 0.05 0.1

× 10

−4

t (ms)

z (μm)

0 0.05 0.1

t (ms)

v (μm/s)

428

Numerical integration of ODEs



t¼t

kþ1

¼ fðt

kþ1

; y

kþ1

Þ

kþ1

 y

;

where h ¼ t

kþ1

 t

. Rearranging, we obtain Euler’s backward formula,

kþ1

¼ y

þ hf t

kþ1

; y

kþ1

ðÞ: (7:29)

This method assumes that the slope of the function yðtÞ in each subinterval is

approximately constant. This assumption is met if the step size h is small enough.

In this forward-marching scheme to solve for y

kþ1

, when y

is known, we need to

know the slope at y

kþ1

. But the value of y

kþ1

is unknown. A difference equation in

which unknown terms are located on both sides of the equation is called an implicit

equation. This can be contrasted with an explicit equation, in which the unknown

term is present only on the left-hand side of the difference equation. Therefore,

Euler’s backward method is sometimes called Euler’s implicit method.

To calculate y

kþ1

at each time step, we need to solve Equation (7.29) for y

kþ1

.If

the equation is linear or quadratic in y

kþ1

, then the terms of the equation can be

rearranged to yield an explicit equation in y

kþ1

. If the backwa rd difference equation

is nonlinear in y

kþ1

, then a nonlinear root-ﬁnding scheme must be used to obtain

kþ1

. In the latter case, the accuracy of the numerical solution is limited by both the

global truncation error of the ODE integration scheme as well as the truncation

error associated with the root-ﬁnding algorithm.

The order of the local truncation error of Euler’s implicit method is the same as

that for Euler’s explicit method, Oh



. Consider the subinterval t

; t

½. The initial

value of y at t

can be expanded in terms of the value of y at t

using the Taylor series:

 hðÞ¼yt

ðÞ¼yt

ðÞy

ðÞh þ

ξðÞh

; ξ ∈ t

; t

½:

Rearranging, we get

ðÞ¼y

þ hf t

; y

ðÞ

ξðÞh

Figure 7.5

Displacement and velocity trajectories for a sphere settling under gravity in Stokes flow. Euler’s explicit method is stable

and physically meaningful for the chosen step size of h =1μs.

0 0.05 0.1

× 10

−4

t (ms)

z (μm)

0 0.05 0.1

t (ms)

v (μm/s)

429

7.2 Euler’s methods

Using Equation (7.29) (k ¼ 0) in the above expansion, we obtain

ðÞ¼y



ξðÞh

ðÞy

¼

ξðÞh

 Oh



The global truncation error for Euler’s implicit scheme is one order of magnitude

lower than the local truncation error. Thus, the convergence rate for global trunca-

tion error is OðhÞ, which is the same as that for the explicit scheme.

An important difference between Euler’s explicit method and the implicit method

is the stability characteristics of the numerical solution. Let’s reconsider the ﬁrst-

order decay problem,

¼λy; λ

The num erical integration formula for this ODE problem, using Euler’s implicit

method, is found to be

kþ1

¼ y

 λhy

kþ1

1 þ λh

: (7:30)

Note that the denominator of Equation (7.30) is greater than unity for any h >0.

Therefore, the numerical solution is guaranteed to mimic the decay of y with time for

any value of h > 0. This example illustrates a useful property of the Euler implicit

numerical scheme.

The Euler implicit numerical scheme is unconditionally stable. The numerical solution will not

diverge if the exact solution is bounded, for any value of h >0.

The global truncation error of the implicit Euler method at t

kþ1

is given by (see

Equation (7.20) for a comparison)

kþ1

ðÞy

kþ1



1  h

∂f

∂y

ðÞy

ðÞþ

The ampliﬁcation factor for the global truncation error of Euler’s implicit method is

1= 1  h

∂f

∂y



.If∂f=∂y

0, i.e. the exact solution is a decaying function, the error is

clearly bounded, and the method is numerically stable for all h.

Example 7.3

The second-order differential equation describing the motion of a sphere settling under gravity in a viscous

medium is re-solved using Euler’s implicit formula. The two simultaneous first-order ODEs are linear. We

will be able to obtain an explicit formula for both y

and y

¼ y

; y

0ðÞ¼0; (7:27)

430

Numerical integration of ODEs

ðρ

 ρ

g 

9μ

; y

0ðÞ¼0: (7:28)

The numerical formulas prescribed by Euler’s backward difference method are

1;kþ1

¼ y

1;k

þ hy

2;kþ1

;

2;kþ1

¼ y

2;k

þ h

ðρ

 ρ

g 

9μ

2;kþ1



The numerical algorithm used to integrate the coupled ODEs is

2;kþ1

2;k

ðρ

ρ

1 þ

9μ

;

1;kþ1

¼ y

1;k

þ hy

2;kþ1

Because of the implicit nature of the algorithm, a general purpose program cannot be written to solve ODEs

using an implicit algorithm. A MATLAB program was written with the express purpose of solving the

coupled ODEs using this algorithm. (Try this yourself.)

Keeping the constants the same, setting h = 0.0001 s, and plotting the numerical solution for the

displacement z and the velocity dz=dt with time (Figure 7.6), we observe that the solution is very well-

behaved. This example demonstrates that the stability characteristics of Euler’s backward method are

superior to those of Euler’s forward method.

7.2.3 Modified Euler’s method

The main disadvantage of Euler’s forward method and backward method is that

obtaining an accurate solution involves considerable computational effort. The accu-

racy of the numerical result (assuming round-off error is negligible compared to

truncation error) increases at the slow rate of OðhÞ. To reduce the error down to

acceptable values, it becomes necessary to work with very small step sizes. The

inefﬁciency in improving accuracy arises because of the crude approximation of

ðtÞ over the entire subinterval with a single value of fðt; yÞ calculated at either the

Figure 7.6

Displacement and velocity trajectories for a sphere settling under gravity in Stokes flow obtained using Euler’s backward

(implicit) method and a step size of h = 0.1 ms.

0 0.5 1

× 10

−3

t (ms)

z (μm)

0 0.5 1

t (ms)

v (μm/s)

431

7.2 Euler’s methods

beginning or end of the subinterval. However, y

ðtÞ is expected to change over an

interval of width h. What is more desirable when numerically integrating an ODE is to

use a value of the slope intermediate to that at the beginning and end of the subinterval

such that it captures the change in the trajectory of y over the subinterval.

The modiﬁed Euler method is a numerical ODE integration method that calculates

the slope at the beginning and end of the subinterval and uses the average of the two

slopes to increment the value of y at each time step. For the ﬁrst-order ODE problem

given below,

¼ ft; yðÞ; y 0ðÞ¼y

;

the numerical integration algorithm is implicit. At time step t

kþ1

, the numerical

approximation to yt

kþ1

ðÞis y

kþ1

, which is calculated using the formula

kþ1

¼ y

þ h

; y

ðÞþft

kþ1

; y

kþ1

ðÞ

: (7:31)

How quickly does the error diminish with a decrease in time step for the modiﬁed

Euler method? Consider the Taylor series expansion of yt

ðÞabout yt

kþ1

ðÞin the

subinterval ½t

; t

kþ1

:

ðÞ¼yt

kþ1

ðÞy

kþ1

ðÞh þ

kþ1

ðÞh



000

ξðÞh

; ξ ∈ t

; t

kþ1

½:

Now, y

kþ1

ðÞ¼ft

kþ1

; yt

kþ1

ðÞðÞ, and y

kþ1

ðÞcan be approximated using the back-

ward ﬁnite difference formula:

kþ1

ðÞ¼

df t

kþ1

; yt

kþ1

ðÞðÞ

kþ1

; yt

kþ1

ðÞðÞft

; yt

ðÞðÞ

þ OðhÞ:

Substituting into the expansion series, we obtain

kþ1

ðÞ¼yt

ðÞþft

kþ1

; yt

kþ1

ðÞðÞh 

kþ1

; yt

kþ1

ðÞðÞft

; yt

ðÞðÞðÞþOh



Rearranging, we get

kþ1

ðÞ¼yt

ðÞþ

kþ1

; yt

kþ1

ðÞðÞþft

; yt

ðÞðÞðÞþOh



kþ1

ðÞ

 y

kþ1

 Oh



The local truncation error for the modiﬁed Euler method is Oh



. The global

truncation error includes the accumulated error from previous steps and is one

order of magnitude smaller than the local error, and therefore is Oh



. The modiﬁed

Euler method is thus called a second-order met hod.

Example 7.4

We use the modified Euler method to solve the linear first-order ODE

¼ t  y; y 0ðÞ¼1: (7:23)

The numerical integration formula given by Equation (7.31) is implicit in nature. Because Equation (7.23) is

linear, we can formulate an equation explicit for y

kþ1

432

Numerical integration of ODEs

kþ1

2  hðÞy

þ hðt

þ t

kþ1

2 þ h

: (7:32)

Starting from t ¼ 0, we obtain approximations for yt

ðÞusing Equation (7.32). A MATLAB program was

written to perform numerical integration of Equation (7.23) using the algorithm given by Equation (7.32).

Equation (7.23) is also solved using Euler’s forward method and Euler’s backward method. The numerical

result at t

¼ 2:8 is tabulated in Table 7.2 for the three different Euler methods and three different step

sizes. The exact solution for yð2:8Þ is 1.9216. The maximum global truncation error encountered during

ODE integration is presented in Table 7.3.

Table 7.3 shows that the global error is linearly dependent on step size for both the forward method and

the backward method. When h is halved, the error also reduces by half. However, global error reduction is



for the modified Euler method. The error decreases by roughly a factor of 4 when the step size is cut

in half. The modified Euler method is found to converge on the exact solution more rapidly than the other

two methods, and is thus more efficient.

Let us consider the stability properties of the implicit modiﬁed Euler method for the

ﬁrst-order decay problem:

¼λy; λ

The step-wise numerical integration formula for this ODE problem is

kþ1

¼ y

þ h

λ y

þ y

kþ1

ðÞ

kþ1

ð2  λhÞy

2 þ λh

: (7:33)

Table 7.2. Numeri cal solution of yðtÞ at t

¼ 2:8 obtained using three

different Euler schemes for solving Equation (7.23)

Euler’s forward

method

Euler’s backward

method

Modiﬁed Euler

method

0.4 1.8560 1.9897 1.9171

0.2 1.8880 1.9558 1.9205

0.1 1.9047 1.9387 1.9213

Table 7.3. Maximum global truncation error observed when using

three different Euler schemes for solving Equation (7.23)

Euler’s forward

method

Euler’s backward

method

Modiﬁed Euler

method

0.4 0.1787 0.1265 0.0098

0.2 0.0804 0.068 0.0025

0.1 0.0384 0.0353 0.000614

433

7.2 Euler’s methods

Equation (7.33) guarantees decay of y with time for any h > 0. The numerical

scheme is unconditionally stable for this problem . This is another example demon-

strating the excellent stability characteristics of implicit numerical ODE integration

methods.

7.3 Runge–Kutta (RK) methods

The Runge–Kutta (RK) methods are a set of explicit higher-order ODE solvers.

The modiﬁed Euler method discussed in Section 7.2.3 was an implicit second-order

method that requires two slope evaluations at each time step. By doubling the

number of slope calculations in the interval, we were able to increase the order of

accuracy by an order of magnitude from OðhÞ, characteristic of Euler’s expli cit

method, to Oh



for the modiﬁed Euler method. This direct correlation between

the number of slope evaluations and the order of the method is exploi ted by the

RK methods. Instead of calculating higher-order derivatives of y, RK numerical

schemes calculate the slope fðt; yÞ at speciﬁc points within each subinterval and

then combine them according to a speciﬁc rule. In this manner, the RK techniques

have a much faster error convergence rate than ﬁrst-order schemes, yet require

evaluations only of the ﬁrst derivative of y. This is one reason why the RK

methods are so popular.

The RK methods are easy to use because the formulas are explicit. However, their

stability characteristics are only slightly better than Euler’s explicit method.

Therefore, a stable solution is not guaranteed for all values of h. When the RK

numerical scheme is stable for the chosen value of h, sub sequent reductions in h lead

to rapid convergence of the numerical approximation to the exact solution. The

convergence rate depends on the order of the RK method. The order of the method is

equal to the number of slope evaluations combined in one time step, when the

number of slopes evaluated is two, three, or four. When the slope evaluations at

each time step exceed four, the correlation between the order of the method and the

number of slopes combined is no longer one-to-one. For example, a ﬁfth-order RK

method requires six slope evaluations at every time step.

In this section, we intro-

duce second-order (RK-2) and fourth-order (RK-4) methods.

7.3.1 Second-order RK methods

The second-order RK method is, as the name suggests, second-order accurate, i.e.

the global truncation error associated with the numerical solution is Oh



. This

explicit ODE integration scheme requires slope evaluations at two points within

each time step. If k

and k

are the slope function s evaluated at two distinct time

points within the subinterval t

; t

kþ1

½, then the general purpose formula of the

RK-2 method is

kþ1

¼ y

þ hc

þ c

ðÞ;

¼ ft

; y

ðÞ; (7:34)

¼ ft

þ p

h; y

þ q

hðÞ:

RK methods of order greater than 4 are not as computationally efﬁcient as RK-4 methods.

434

Numerical integration of ODEs

The values of the constants c

; c

; p

; and q

are determined by mathematical

constraints, or rules, that govern this second-order method. Let’s investigate these

rules now.

We begin with the Taylor series expansion for yt

kþ1

ðÞexpanded about yt

ðÞusing

a step size h:

kþ1

ðÞ¼yt

ðÞþy

ðÞh þ

ðÞh

þ Oh



The second derivative, y

tðÞ, is the ﬁrst derivative of fðt; yÞ and can be expressed in

terms of partial derivatives of fðt; yÞ:

tðÞ¼f

t; yðÞ¼

∂ft; yðÞ

∂t

∂ft; yðÞ

∂y



Substituting the expansion for y

ðÞinto the Taylor series expansion, we obtain a

series express ion for the exact solution at t

kþ1

ðÞ¼yt

ðÞþft

; y

ðÞh þ

∂ft; yðÞ

∂t

∂ft; yðÞ

∂y

; y

ðÞ



þ Oh



: (7:35)

To ﬁnd the values of the RK constants, we must compare the Taylor series expansion

of the exact solution with the numerical approximation provided by the RK-2

method. We expand k

in terms of k

using the two-dimensional Taylor series:

¼ ft

; y

ðÞþp

∂ft

; y

ðÞ

∂t

þ q

∂ft

; y

ðÞ

∂y

þ Oh



Substituting the expressions for k

and k

into Equations (7.34) for y

kþ1

, we obtain

kþ1

¼ y

þ hc

; y

ðÞþc

; y

ðÞð

þc

∂ft

; y

ðÞ

∂t

þ c

hf t

; y

ðÞ

∂ft

; y

ðÞ

∂y

þ Oh





kþ1

¼ y

þ ft

; y

ðÞc

þ c

ðÞh þ h

∂ft

; y

ðÞ

∂t

þ c

∂ft

; y

ðÞ

∂y

; y

ðÞ



þ Oh



(7:36)

Comparison of Equations (7.35) and (7.36) yields three rules governing the RK-2

constants:

þ c

¼ 1;

;

For this set of three equations in four variables, an inﬁnite number of solutions exist.

Thus, an inﬁnite number of RK−2 schemes can be devised. In practice, a family of

RK-2 methods exists, and we discuss two of the most common RK-2 schemes: the

explicit modiﬁed Euler method and the midpoint method.

435

7.3 Runge–Kutta (RK) methods

Modified Euler method (explicit)

This numerical scheme is also called the trapezoidal rule and Heun’s method.It

uses the same numerical integration formula as the implicit modiﬁed Euler

method discussed in Section 7.2.3. However, the algori thm used to calculate

the slope of y at t

kþ1

is what sets this method apart from the one discussed

earlier.

Setting c

¼ 1=2, we obtain the following values for the RK−2 parameters:

; p

¼ 1; q

¼ 1:

Equations (7.34) simplify to

kþ1

¼ y

þ k

ðÞ;

¼ ft

; y

ðÞ; (7:37)

¼ ft

þ h; y

þ k

hðÞ:

This RK−2 method is very sim ilar to the implicit modiﬁed Euler method. The

only difference between this integration scheme and the implicit second-or der

method is that he re the value of y

kþ1

on the right-hand side of the equation is

predicted using Euler’s explicit method, i.e. y

kþ1

¼ y

þ hk

. With replacement of

the right-hand side term y

kþ1

with known y

terms, the integration method is

rendered explicit. The global error for the explicit modiﬁed Euler method is still



; however, the actual error may be slightly larger in magnitude than that

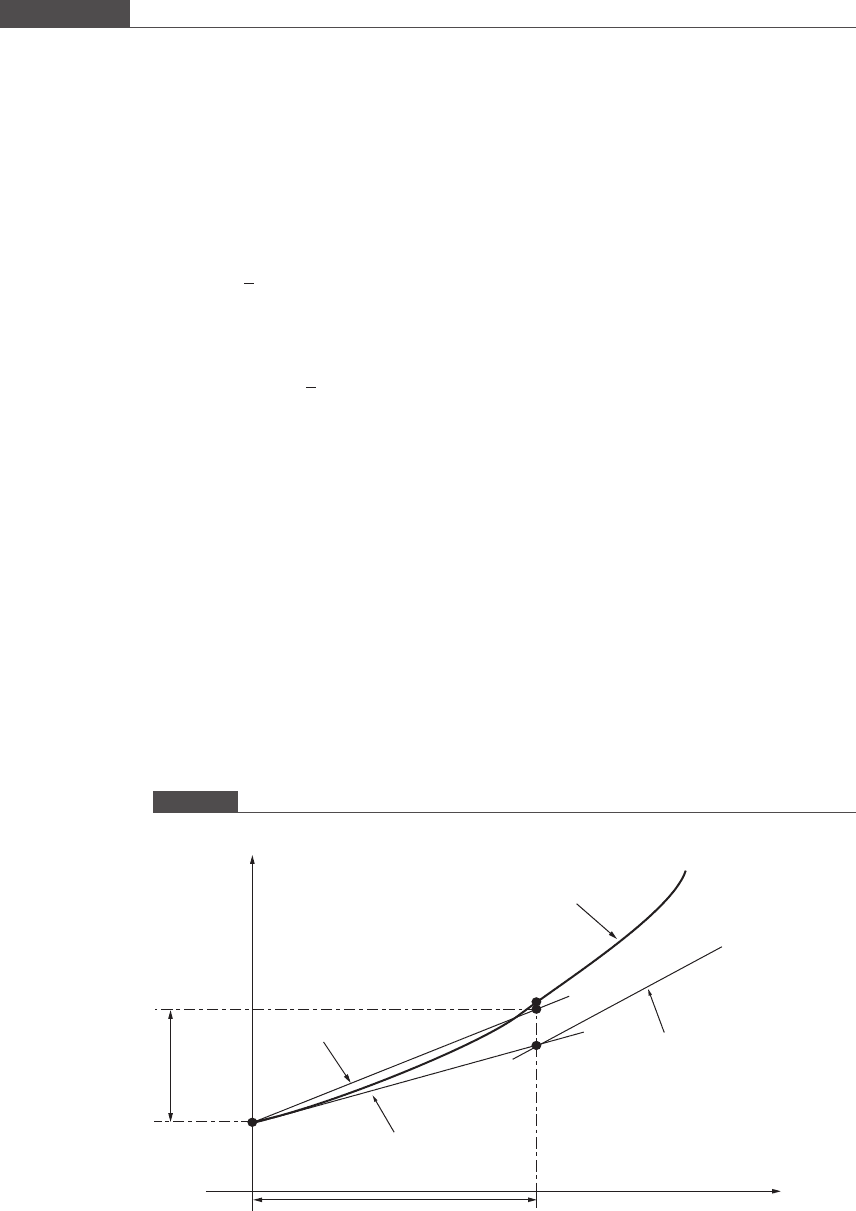
generated by the implicit method. Figure 7.7 illustrates the geometric interpreta-

tion of Equations (7.37).

Figure 7.7

Numerical integration of an ODE using the explicit modified Euler method.

y(t

)

slope: k

= f(t

, y

)

slope: k

= f(t

, y

+ hf(t

, y

))

h(k

+ k

)/2

y(t)

Exact solution

slope = ½(k

+ k

)

436

Numerical integration of ODEs