King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

Midpoint method

The midpoint method uses the slope at the midpoint of the interval, i.e. t

þ h=2to

calculate the approximation to yt

kþ1

ðÞ. The value of y at the midpoint of the interval

is estimated using Euler’s explicit formula.

Setting c

¼ 1, we obtain the followi ng values for the RK−2 parameters:

¼ 0; p

; q

Equations (7.34) simplify to

kþ1

¼ y

þ hk

;

¼ ft

; y

ðÞ; (7:38)

¼ ft

; y



Numerical ODE integration via the midpoint method is illustrated in Figure 7.8.

Now consider the stability properties of the explicit modiﬁed Euler method for the

ﬁrst-order decay problem

¼λy; λ

The numerical integration formula for this ODE problem using the explicit modiﬁed

Euler’s method is

kþ1

¼ y

þ h

λ y

þ y

 λhy

ðÞðÞ

kþ1

¼ 1  λh þ



: (7:39)

Figure 7.8

Numerical integration of an ODE using the midpoint method.

h/2

y(t

)

slope: k

= f(t

, y

)

slope: k

f(t

h/2

, y

+ (h/2)k

)

y(t)

Exact solution

slope = k

h/2

437

7.3 Runge–Kutta (RK) methods

A bounded solution will be obtained if

 1  1  λh þ

 1:

Let x ¼ λh. Values of x that simultaneously satisfy the two quadratic equations

speciﬁed by the condition above ensure a stable numerical result.

The ﬁrst equation, xðx  2Þ0, requires that 0  x  2.

The second equation x

 2x  4  0 requires that 1:236  x  3:236.

Therefore, 0  λh  2 is the numerical stabi lity requirement for this problem

when using the explicit modiﬁed Euler method. The stability characteristics of

this RK − 2 method for the ﬁrst-order decay problem are the same as those of the

explicit Euler method. While the RK−2 method will converge faster to the exact

solution compared to the forward Euler method, it requires an equally small h

value to prevent instability from creeping into the numerical solution. It is left to

the reader to show that the numerical stability properties of the midpoint method are

the same as that of the explicit modiﬁed Euler method for the ﬁrst-order decay

problem.

7.3.2 Fourth-order RK methods

Fourth-order RK methods involve four slope evaluations per time step, and have a

local convergence error of Oh



and a global convergence error of Oh



. The

numerical scheme for the RK−4 methods is

kþ1

¼ y

þ hc

þ c

ðÞ;

¼ ft

; y

ðÞ;

¼ ft

þ p

h; y

þ q

hðÞ;

¼ ft

þ p

h; y

þ q

h þ q

hðÞ;

¼ ft

þ p

h; y

þ q

h þ q

hðÞ:

The derivation of the 11 equations governing the 13 constants is too tedious and

complicated to be performed here. A popular fourth-order RK method in use is the

classical method presented below:

kþ1

¼ y

þ 2k

þ k

ðÞ

¼ ft

; y

ðÞ

¼ ft

þ 0:5h; y

þ 0:5k

hðÞ

¼ ft

þ 0:5h; y

þ 0:5k

hðÞ

¼ ft

þ h; y

þ k

hðÞ

(7:40)

Example 7.5

We use the classical RK−4 method and the midpoint method to solve the linear first-order ODE

¼ t  y; y 0ðÞ¼1: (7:23)

Functions created to perform single ODE integration by the midpoint method and the classical RK−4

method are listed below. The ODE function that evaluates the right-hand side of Equation (7.23) is listed in

438

Numerical integration of ODEs

Program 7.2. Another MATLAB program can be created to call these numerical ODE solvers, or the

functions can be called from the MATLAB Command Window.

MATLAB program 7.5

function [t, y] = midpointmethod(odefunc, tf, y0, h)

% Midpoint (RK−2) method is used to solve a ﬁrst-order ODE

% Input variables

% odefunc : name of the function that calculates f(t, y)

%tf:ﬁnal time or size of interval

% y0 : y(0)

% h : step size

% Output variables

t = [0:h:tf]; % vector of time points

y = zeros(size(t)); % dependent variable vector

y(1) = y0; % indexing of vector elements begins with 1 in MATLAB

% Midpoint method for solving ﬁrst-order ODE

for k = 1:length(t)-1

k1 = feval(odefunc, t(k), y(k));

k2 = feval(odefunc, t(k) + h/2, y(k) + h/2*k1);

y(k+1) = y(k) + h*k2;

end

MATLAB program 7.6

function [t, y] = RK4method(odefunc, tf, y0, h)

% Classical RK−4 method is used to solve a ﬁrst-order ODE

% Input variables

% odefunc : name of the function that calculates f(t, y)

%tf:ﬁnal time or size of interval

% y0 : y(0)

% h : step size

% Output variables

t = [0:h:tf]; % vector of time points

y = zeros(size(t)); % dependent variable vector

y(1) = y0; % indexing of vector elements begins with 1 in MATLAB

%RK−4 method for solving ﬁrst-order ODE

for k = 1:length(t)-1

k1 = feval(odefunc, t(k), y(k));

k2 = feval(odefunc, t(k)+ h/2, y(k) + h/2*k1);

k3 = feval(odefunc, t(k)+ h/2, y(k) + h/2*k2);

k4 = feval(odefunc, t(k)+ h, y(k) + h*k3);

y(k+1) = y(k) + h/6*(k1 + 2*k2 + 2*k3 + k4);

end

The final value at t

¼ 2:8 and maximum global error is tabulated in Table 7.4 for the two RK methods and

two different step sizes. The exact solution for yð2:8Þ is 1.9216.

From the results presented in Table 7.4, it is observed that, in the midpoint method, the maximum

truncation error reduces by a factor of 4:65  2

upon cutting the step size in half. In the RK−4 method,

439

7.3 Runge–Kutta (RK) methods

the maximum truncation error reduces by a factor of 18:6  2

upon cutting the step size in half. For

one uniform step size, the number of function calls, and therefore the computational effort, is twice as

much for the RK−4 method compared to the RK−2 method. Now compare the accuracy of the two

methods. The total number of slope evaluations over the entire interval performed by the RK−4 method for

h = 0.4 is equal to that performed by the midpoint method at h = 0.2. However, the RK−4 method is

0:0057=2:1558  10

4

¼ 27 times more accurate at h = 0.4 than the midpoint method is at h = 0.2.

Thus, the fourth-order method is much more efficient than the second-order method.

The RK−4 method can be easily adapted to solve coupled ﬁrst-order ODEs. The set

of equations for solving the two coupled ODEs,

¼ f

t; y

; y

ðÞ;

¼ f

t; y

; y

ðÞ;

1;1

¼ f

; y

1;k

; y

2;k



;

2;1

¼ f

; y

1;k

; y

2;k



;

1;2

¼ f

þ 0:5h; y

1;k

þ 0:5k

1;1

h; y

2;k

þ 0:5k

2;1



;

2;2

¼ f

þ 0:5h; y

1;k

þ 0:5k

1;1

h; y

2;k

þ 0:5k

2;1



;

1;3

¼ f

þ 0:5h; y

1;k

þ 0:5k

1;2

h; y

2;k

þ 0:5k

2;2



;

2;3

¼ f

þ 0:5h; y

1;k

þ 0:5k

1;2

h; y

2;k

þ 0:5k

2;2



;

1;4

¼ f

þ h; y

1;k

þ k

1;3

h; y

2;k

þ k

2;3



;

2;4

¼ f

þ h; y

1;k

þ k

1;3

h; y

2;k

þ k

2;3



;

1;kþ1

¼ y

1;k

1;1

þ 2k

1;2

þ 2k

1;3

þ k

1;4



;

2;kþ1

¼ y

2;k

2;1

þ 2k

2;2

þ 2k

2;3

þ k

2;4



(7:41)

These equations are used to solve the coupled ODE system in Box 7.1A.

7.4 Adaptive step size methods

An important goal in developing a nume rical ODE solver (or, in fact, any numerical

method) is to maximize the computational efﬁciency. We wish to attain the desired

accuracy of the solution with the least amount of computational effort. In earlier

Table 7.4. Numeri cal solution of yðtÞ at t

¼ 2:8 and maximum global truncation error

obtained using two different RK schemes to solve Equation (7.23) numerically

h Midpoint method RK−4 method

Numerical

solution of yð2:8Þ

Maximum global

truncation error

Numerical

solution of yð2:8Þ

Maximum global

truncation error

0.4 1.9345 0.0265 1.9217 2.1558 × 10

−4

0.2 1.9243 0.0057 1.9216 1.159 × 10

−5

440

Numerical integration of ODEs

Box 7.1B HIV–1 dynamics in the bloodstream

We make the following substitutions for the dependent variables:

¼ T



; y

¼ V

; y

¼ V

The set of three first-order ODEs listed below are solved using the RK–4 method:

¼ 0:05y

 0:5y

;

¼3:0y

;

 30y

 3:0y

The initial concentrations of T



, V

, and V

are

ðt ¼ 0Þ¼100=μl

ðt ¼ 0Þ¼0=μl



ðt ¼ 0Þ¼10 infected cells=μl. (Haase et al., 1996).

The function program HIVODE.m is written to evaluate the right-hand side of the ODEs. The RK–4

method from Program 7.6 must be vectorized in the same way that Euler ’s explicit method was (see

Programs 7.1 and 7.3) to solve coupled ODEs. The main program calls the ODE solver

RK4methodvectorized and plots the time-dependent behavior of the variables.

MATLAB program 7.7

% Use the RK-4 method to solve the HIV dynamics problem

clear all

% Variables

y0(1) = 10; % initial value of T*

y0(2) = 100; % initial value of V1

y0(3) = 0; % initial value of Vx

tf = 5; % interval size (day)

h = 0.1; % step size (day)

% Call ODE Solver

[t, y] = RK4methodvectorized(‘HIVODE’, tf, y0, h);

% Plot Results

ﬁgure;

subplot(1,3,1)

plot(t,y(1,:),‘k-’,‘LineWidth’,2)

set(gca,‘FontSize’,16,‘LineWidth’,2)

xlabel(‘{\itt} in day’)

ylabel(‘{\itT}^* infected cells/ \muL’)

subplot(1,3,2)

plot(t,y(2,:),‘k-’,‘LineWidth’,2)

set(gca,‘FontSize’,16,‘LineWidth’,2)

xlabel(‘{\itt} in day’)

ylabel(‘{\itV}_1 virions/ \muL’)

subplot(1,3,3)

plot(t,y(3,:),‘k-’,‘LineWidth’,2)

441

7.4 Adaptive step size methods

set(gca,‘FontSize’,16,‘LineWidth’,2)

xlabel(‘{\itt} in day’)

ylabel(‘{\itV}_X noninfectious virus particles/ \muL’)

MATLAB program 7.8

function [t, y] = RK4methodvectorized(odefunc, tf, y0, h)

% Classical RK-4 method is used to solve coupled ﬁrst-order ODEs

% Input variables

% odefunc : name of the function that calculates f(t, y)

%tf:ﬁnal time or size of interval

% y0 : vector of initial conditions y(0)

% h : step size

% Other variables

n = length(y0); % number of dependent time-varying variables

% Output variables

t = [0:h:tf]; % vector of time points

y = zeros(n, length(t)); % dependent variable vector

y(:,1) = y0; % initial condition at t = 0

% RK-4 method for solving coupled ﬁrst-order ODEs

for k = 1:length(t)-1

k1 = feval(odefunc, t(k), y(:,k));

k2 = feval(odefunc, t(k)+ h/2, y(:,k) + h/2*k1);

k3 = feval(odefunc, t(k)+ h/2, y(:,k) + h/2*k2);

k4 = feval(odefunc, t(k)+ h, y(:,k) + h*k3);

y(:,k+1) = y(:,k) + h/6*(k1 + 2* k2 + 2* k3 + k4);

end

MATLAB program 7.9

function f = HIVODE(t, y)

% Evaluate slope f(t,y) of coupled ODEs for HIV-1 dynamics in bloodstream

% Constants

k = 2e-4; % uL/day/virions

N = 60; % virions/cell

delta = 0.5; % /day

c = 3.0; % /day

T = 250; % noninfected cells/uL

f = [k*T*y(2)-delta*y(1); -c*y(2); N*delta*y(1)-c*y(3)];

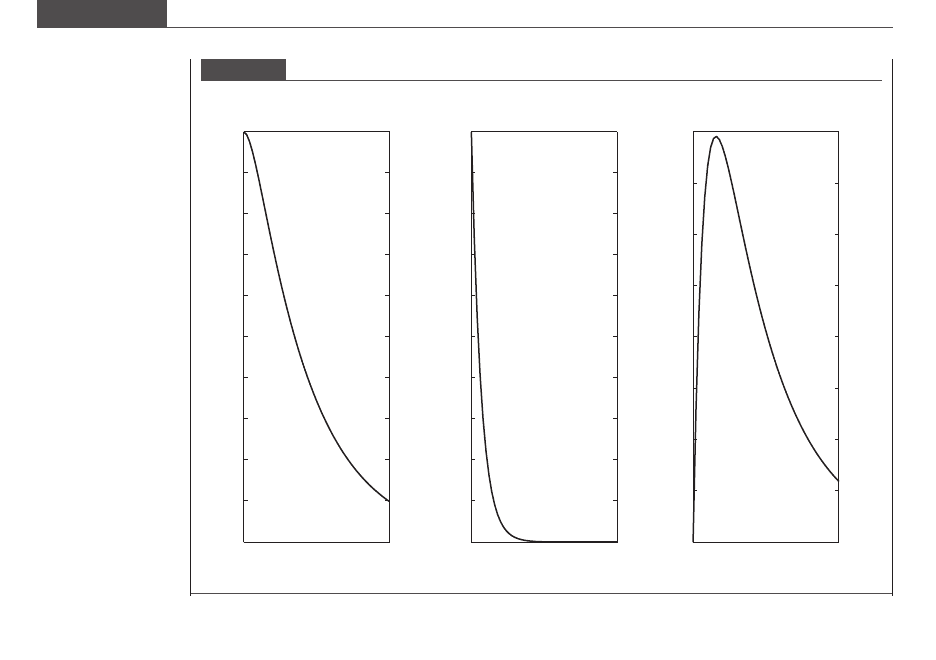
Figure 7.9 shows the rapid effect of the drug on the number of infected cells, and the number of

infectious and non-infectious virus particles in the bloodstream. The number of infected cells in the

bloodstream plunges by 90% after five days of ritonavir treatment.

There are a number of simplifying assumptions of the model, particularly (1) virus counts in other

regions of the body such as lymph nodes and tissues are not considered in the model and (2) the

number of non-infected cells is assumed to be constant over five days.

442

Numerical integration of ODEs

sections of this chapter, we discussed two ways to improve the accuracy of a numerical

solution: (1) reduce the step size and (2) increase the order of the ODE integration

routine. Our earlier discussions have focused on closing the gap between the numerical

approximation and the exact solution. In practice, we seek numerical solutions that

approach the true solution within a speciﬁed tolerance. The tolerance criterion sets a

lower limit on the accuracy that must be met by an ODE solver. If a numerical method

produces a solution whose numerical error is one or more orders of magnitude less than

the tolerance requirement, then more computational effort in terms of time and resour-

ces to obtain a solution has been expended than required. We wish to minimize wasteful

computations that add little, if any, value to the solution. Using a ﬁxed time step

throughout the integration process is an example of unnecessary computational work.

An ODE solver that uses a ﬁxed time step must choose a time step that resolves the most

rapid change or capricious behavior of the slope function to the desired accuracy. For

other regions of the time interval, where the slope evolves more slowly, the ﬁxed step size

in use is much smaller than what is required to keep the error within the tolerance limit.

The integration thus proceeds more slowly than necessary in these subintervals.

To integrate more efﬁciently over the time interval, once can adjust the step size h at

each time step. The optimal step size becomes a function of time and is chosen based on

the local truncation error generated by the solution at each instant in time. ODE solvers

that optimize the step size as an integration proceeds along the interval are known as

adaptive step size methods. There are several ways to estimate the local truncation error,

which measures the departure of the numerical solution from the exact solution assum-

ing that the solution at the previous time point is known with certainty. In this section, we

focus our discussion on adaptive step size algorithms for RK methods.

Figure 7.9

Effect of ritonavir treatment on viral particle concentration in the bloodstream.

0 5

t (da

T * infected cells (μl)

0 5

100

t (days)

virions (μl)

t (days)

0 5

non-infectious virus particles (μl)

443

7.4 Adaptive step size methods

One technique to measure local truncation error is to solve the ODE at time t

kþ1

using a step size h, and then to re-solve the ODE at the same time point using a step

size h=2. The difference between the two numerical solutions provides an estimate of

the local truncation error at time step t

kþ1

. The exact solution at t

kþ1

can be

expressed in terms of the numerical solution y

, assuming that the solution at the

time point t

is known exactly, i.e. yt

ðÞ¼y

. For a step size h,

kþ1

ðÞ¼y

kþ1

þ Mh

nþ1

The second term on the right-hand side is the local truncation error. For a step size of

h=2, the integration must be performed twice to reach t

kþ1

. If we assume that M is

constant over the time step, and the accumulation of other errors when stepping

twice to reach the end of the subinterval is negligible, then

kþ1

ðÞz

kþ1

þ M



nþ1

þM



nþ1

;

where z

kþ1

is the numerical solution obtained with step size h=2. Taking the differ-

ence of the two numerical solutions, z

kþ1

 y

kþ1

, we get an estimate of the local

truncation error for a step size of h:

nþ1

 1

kþ1

 y

kþ1

ðÞ: (7:42)

If E is the tolerance prescribed for the local error, then E can be set equal to Mh

nþ1

opt

where h

opt

is the optimum step size needed attain the desired accuracy. Substituting

M ¼ E=h

nþ1

opt

in Equation (7.42), we get

opt



nþ1

 1



kþ1

 y

kþ1

: (7:43)

Equation (7.43) can be used at each time step to solve for h

opt

. However, there is a

disadvantage in using two unequal step sizes at each time step to estimate the

truncation error. The ODE integration must be performed over the same subinterval

three times just to optimize the step size. Additionally, if the newly calculated h

opt

less than h= 2, then the integ ration step must be repeated one more time with h

opt

the current time point to obtain the more accurate numerical solution.

Evaluating a numerical solution at any time point using two different step sizes is

very useful however when assessing the stability of the numerical method. When the

numerical solution obtained with two different step sizes does not differ appreciably,

one can be conﬁdent that the method is numerically stable at that time point. If the

two solut ions differ signiﬁcantly from each other, even for very small step sizes, one

should check for numerical instabilities, possibly by using a more robust ODE solver

to verify the numerical solution.

The Runge–Kutta–Fehlberg (RKF) method is an efﬁcient strategy for evaluating the

local error at each time point. This method advances from one time point to the next

using one step size and a pair of RK methods, with the second method of one order

higher than the ﬁrst. Two numerical solutions are obtained at the current time point. For

example, a fourth-order RK method can be paired with a ﬁfth-order RK method in such

a way that some of the slope evaluations for either method share the same formula. An

RK−4 method requires at least four slope evaluations to achieve a local truncation error

of Oh



.AnRK−5 method requires at least six slope evaluations to achieve a local

truncation error of Oh



. If the two methods are performed independently of each

444

Numerical integration of ODEs

other, a total of ten slope evaluations are necessary to calculate two numerical solutions,

one more accurate than the other. However, the RKF45 method that pairs a fourth-

order method with a ﬁfth-order method requires only six total slope evaluations since

slopes k

; k

,andk

aresharedamongthetwomethods.

Here, we demonstrate an RKF23 method that pairs a second-order method with a

third-order method, and requires only three slope evaluations. The RK−2 method in this

two-ODE solver combination is the modiﬁed Euler method or trapezoidal rule (Equation

(7.37)). The local truncation error associated with each time step is Oh



.Wehave

kþ1

¼ y

þ k

ðÞ:

The RK−3 method is

¼ ft

; y

ðÞ;

¼ ft

þ h; y

þ k

hðÞ;

¼ ft

þ 0:5h; y

þ 0:25k

h þ 0:25k

hðÞ;

kþ1

¼ y

þ k

þ 4k

ðÞ:

The local truncation error associated with each time step is Oh



. The RK−2 and

RK−3 methods share the slopes k

and k

. If we may assume that Oh



local errors

are negligible compared to the Oh



local errors, then, on subtracting the RK−3

solution from the RK−2 numerical approximation, we obtain

þ k

ðÞ

þ k

þ 4k

ðÞ¼

þ k

 2k

ðÞMh

The tolerance for the local error is represented by E. Since E ¼ Mh

opt

, we have

opt



ðh=3Þ k

þ k

 2k

ðÞ

The optimal step size calculation is only approximate since global errors are

neglected. For this reason, a safety factor α is usually included to adjust the pre-

diction of the correct step size. Adaptive step size algorithms typically avoid increas-

ing the step size more than necessary. If the current step size is larger than the

calculated optim um, the algorithm must recalcu late the numerical solution using the

smaller step size h

opt

. If the current step size is smaller than h

opt

, then no recalculation

is done for the cu rrent step, and the step size is adjusted at the next time step.

MATLAB offers a variety of ODE solvers that perform numerical integration of a

system of ordinary differential equations. ODE solvers ode23 and ode45 use explicit

RK adaptive step size algorithms to solve initial-value problems. The ode45 function

uses paired RK−4andRK−5 routines to integrate ODEs numerically and is based on the

algorithm of Dormand and Prince. It is recommended that this function be tried when

ﬁrst attempting to solve an ODE problem. The ode23 function uses paired RK−2and

RK−3 routines (Bogacki and Shampine algorithm) to integrate ODEs numerically, and

canbemoreefﬁcientthanode45 when required tolerances are higher.

Using MATLAB

All MATLAB ODE solvers (except for ode15i) share the same syntax. This makes

it easy to switch from one function call to another. The simplest syntax for a

MATLAB ODE solver is

445

7.4 Adaptive step size methods

[t, y]= odexxx(odefunc, tf, y0), or

[t, y]= odexxx(odefunc, [t0 tf], y0)

The input parameters for an ODE solver are as follows.

odefunc: The name of the user-deﬁned function that evaluates the slope f ðt; yÞ,

entered within single quotation marks. For a coupled ODE problem,

this ODE function shou ld output a column vector whose elements are

the ﬁrst derivatives of the dependent variables, i.e. the right-hand side

of the ODE equations.

[t0 tf]: The beginning and ending tim e points of the time interval.

y0: The value of the dependent variable(s) at time 0. If there is more than

one dependent variable, y0 should be supplied as a column vector,

otherwise y0 is a scalar. The order in which the initial values of the

variables should be listed must correspond to the order in which their

slopes are calculated in the ODE function odefunc.

The output variables are as follows.

t: A column vector of the time points at which the numerical solution has been

calculated. The time points will not be uniformly spaced since the time step is

optimized during the integration. If you require a solution at certain time points

only, you should specify a vector containing speciﬁc time points in place of the

time interval [t0, tf], e.g.

[t, y]= odexxx(odefunc, [0:2:10], y0)

The numerical solution y will be output at these six time points, although higher

resolution may be used during integration.

y: For a single ODE problem, this is a column vector containing the solution at

time points recorded in vector t. For a coupled ODE problem, this is a matrix with

each column representing a different dependent variable and each row repres enting a

different time point that corresponds to the same row of t.

The optimal step size is chosen such that the local truncation error ekðÞat step k,

estimated by the algorithm, meets the following tolerance criteria:

e(k) ≤ max(RelTol * |y(k)|, AbsTol)

The default value for the relative tolerance RelTol is 10

−3

. The default value for

the absolute tolerance AbsTol is 1 × 10

−6

.For y

3

the relative tolerance will set

the tolerance limit. For y

3

, the absolute tolerance will control the error. For

 1, it is recommended that you change the default value of AbsTol accordingly.

Sometimes you may want to suggest an initial step size or specify the maximum

step size (default is 0:1 t

 t

ðÞ) allowed during integration. To change the default

settings of the ODE solver you must create an options structure and pass that

structure along with other parameters to the odexxx function. A structure is a data

type that is somewhat like an array except that it can contain different types of data

such as character arrays, numbers, and matrices each stored in a separate ﬁeld. Each

ﬁeld of a structure is given a name. If the name of the structure is Options, then

RelTol is one ﬁeld and its contents can be accessed by typing Options.RelTol.

To create an options structure, you will need to use the function odese t. The

syntax for odeset is

446

Numerical integration of ODEs