King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB
Подождите немного. Документ загружается.


options = odeset(‘parameter1’, ‘value1’, ‘parameter2’, ‘value2’, ...)
For example, you can set the relative tolerance by doing the following. Create an
options structure,
options = odeset(‘RelTol’, 0.0001);
Now pass the newly created options structure to the ODE solver using the syntax
[t, y]= ode45(odefunc, [t0 tf], y0, options)
There are a variety of features of the ODE solvers that you can control using the
options structure. For more information, see MATLAB help.
Values of constants or parameters can be passed to the function that calculates the
right-hand side of Equation (7.26). These parameters should be listed after the
options argument. If you do not wish to supply an options structure to the ODE
solver, you should use [] in its place. When creating the defining line of the function
odefunc, you must pass an additional argument called flag, as shown below:
f = odefunc(t, y, flag, p1, p2)
where p1 and p2 are additional parameters that are passed from the calling pro-
gram. See Box 7.3B for an example that uses this syntax .
Box 7.1C HIV–1 dynamics in the blood stream
We re-solve the coupled ODE problem using the MATLAB ode45 function:
dy
1
dt
¼ 0:05y
2
0:5y
1
;
dy
2
dt
¼3:0y
2
;
dy
3
dt
¼ 30y
1
3:0y
3
:
The initial concentrations of T*, V
1
, and V
X
are y
1
0ðÞ¼10; y
2
0ðÞ¼100; y
3
0ðÞ¼0.
The ode45 function can be called either in a script file or in the Command Window:
44
[t, y] = ode45(‘HIVODE’, 5.0, [10; 100; 0]);
The first five and last five time points for integration are
44
t(1:5)
44
t(end-4:end)
ans = ans =
1.0e-006 * 4.8440
0 4.8830
0.1675 4.9220
0.3349 4.9610
0.5024 5.0000
0.6698
The time step increases by five orders of magnitude from the beginning to the end of the interval. The
number of infected cells, infectious viral particles, and non-infectious viral particles at t = 5 days is
44
y(end, :)
ans –
0.9850 0.0000 11.8201
447
7.4 Adaptive step size methods

Box 7.2B Enzyme deactivation in industrial processes
Defining y
1
S and y
2
E
total
, we rewrite the first-order differential equations as follows:
dy
1
dt
¼
k
2
y
2
y
1
K
m
þ y
1
;
dy
2
dt
¼
k
d
y
2
1 þ y
1
=K
m
;
where
k
2
¼ 21 M/s/e.u. (e.u. enzyme units)
K
m
¼ 0:004 M
k
d
¼ 0:03/s.
The initial conditions are y
1
¼ 0:05 M and y
2
¼ 1 10
6
units.
enyzmedeact is an ODE function written to evaluate the right-hand side of the coupled ODE
equations. A script file is written to call ode45 and plot the result.
MATLAB program 7.10
% Use ode45 to solve the enzyme deactivation problem.
clear all
% Variables
y0(1) = 0.05; % M
y0(2) = 1e-6; % units
tf = 3600; % s
% Call ODE Solver
[t, y] = ode45(‘enzymedeact’, tf, y0);
% Plot Results
figure;
subplot(1,2,1)
plot(t,y(:,1),‘k-’,‘LineWidth’,2)
set(gca,‘FontSize’,16,‘LineWidth’,2)
xlabel(‘{\itt} in sec’)
ylabel(‘{\itS} in M’)
subplot(1,2,2)
plot(t,y(:,2),‘k-’,‘LineWidth’,2)
set(gca,‘FontSize’,16,‘LineWidth’,2)
xlabel(‘{\itt} in sec’)
ylabel(‘{\itE}_t_o_t_a_l in units’)
MATLAB program 7.11
function f = enzymedeact(t, y)
% Evaluate slope f(t,y) of coupled ODEs for enzyme deactivation
% Constants
k2 = 21; % M/s/e.u.
Km = 0.004; % M
kd = 0.03; % s-1
f = [-k2*y(1)*y(2)/(Km + y(1));-kd*y(2)/(1 + y(1)/Km)];
448
Numerical integration of ODEs
Box 7.3B Dynamics of an epidemic outbreak
Two sets of parameters are chosen to study the dynamics of the spread of disease in a population of
100 000.
Case (1) k =1× 10
−5
and γ = 4. This set of values represents a disease that spreads easily and
recovery is rapid, e.g. flu.
Case (2) k =5× 10
−8
and γ = 4000. This set of values represents a disease that spreads with
difficulty yet a person remains infectious for a longer period of time, e.g. diseases that are
spread by contact of bodily fluids.
The birth and death rates are β ¼ 0:0001; and μ ¼ 0:00001, respectively. Defining y
1
S,
y
2
D, and y
3
I, we rewrite the first-order differential equations as
dy
1
dt
¼ky
1
y
2
þ β y
1
þ y
3
ðÞμy
1
;
dy
2
dt
¼ ky
1
y
2
1
γ
y
2
;
dy
3
dt
¼
1
γ
y
2
μy
3
:
The MATLAB ODE solver ode23 is used to solve this problem. For case 1, we observe from
Figure 7.11 that the disease becomes an epidemic and spreads through the population within a
month. As large sums of people become sick, recover, and then become immune, the disease
disappears because there is a lack of people left to spread the disease.
For the second case, because the recovery period is so long, we must modify the equations to
account for people who die while infected. From Figure 7.12, we see that, in 7 years, most of the
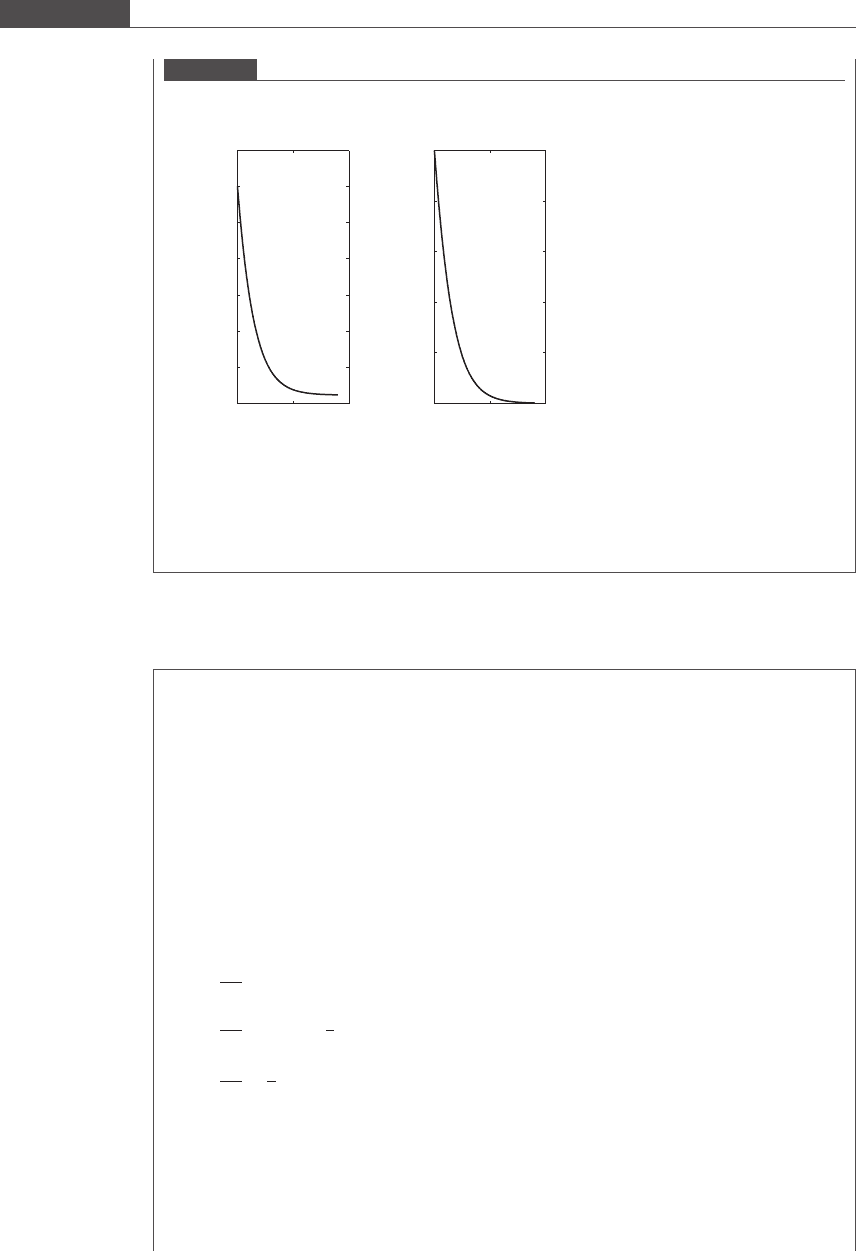
Figure 7.10 plots the drop in concentration with time. At t = 440 s, the active enzyme concentration
reduces to half its starting value. Note the quick deactivation of the enzyme in comparison to
consumption of the substrate. The enzymatic process needs to be modified to increase the life of the
enzyme.
Figure 7.10
Decrease in concentration of substrate and active enzyme with time.
0 2000 4000
0.038
0.04
0.042
0.044
0.046
0.048
0.05
0.052
t (s)
S (M)
0 2000 4000
0
0.2
0.4
0.6
0.8
1
× 10
−6
t (s)
E
total
(units)
449
7.4 Adaptive step size methods
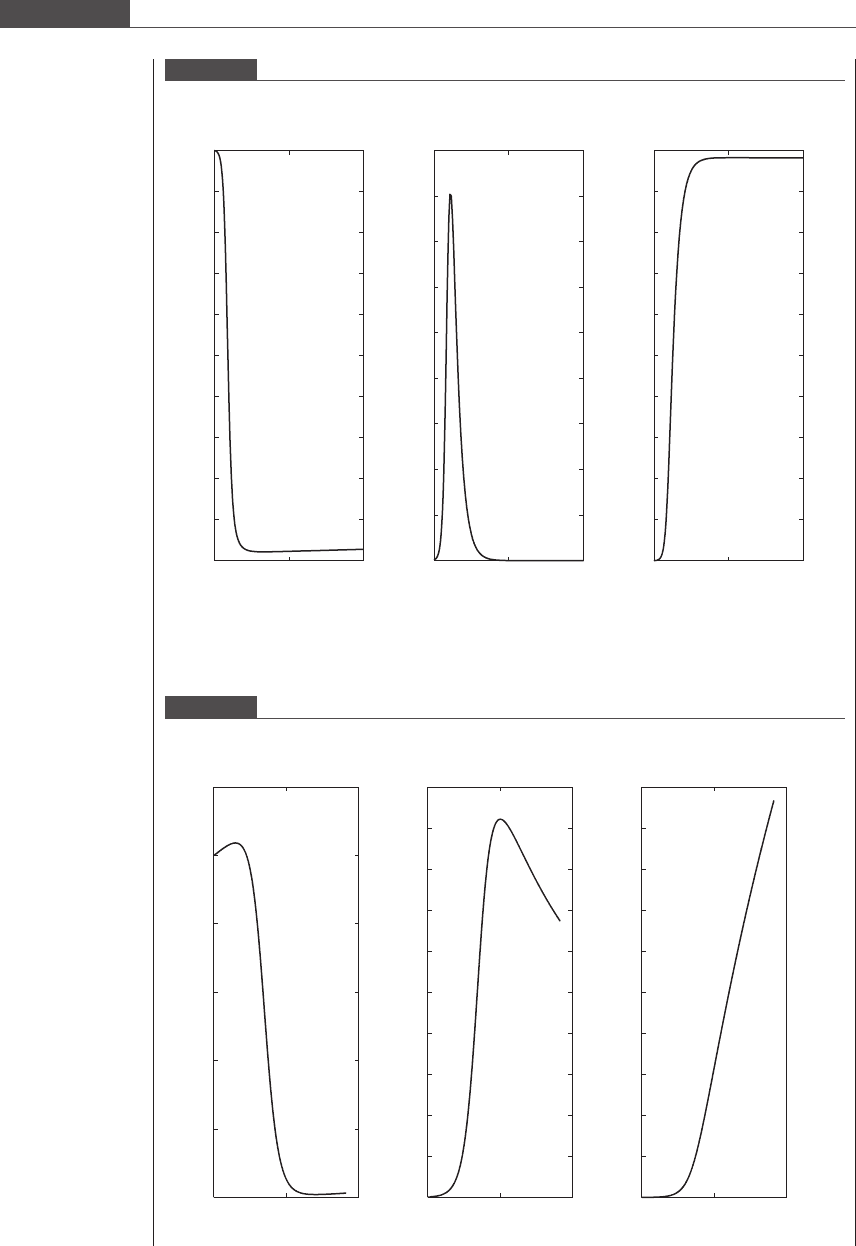
Figure 7.11
Spread of disease among individuals in an isolated population for case 1.
0 50 100
0
1
2
3
4
5
6
7
8
9
10
× 10
4
t (days)
S
0 50 100
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
× 10
4
× 10
4
t (days) t (days)
D
0 50 100
0
1
2
3
4
5
6
7
8
9
10
I
Figure 7.12
Spread of disease among individuals in an isolated population for case 2.
0 2000 4000
0
2
4
6
8
10
12
× 10
4
t (days)
S
0 2000 4000
0
1
2
3
4
5
6
7
8
9
10
× 10
4
t (days) t (days)
D
0 2000 4000
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
× 10
4
I
450
Numerical integration of ODEs

MATLAB program 7.12
% Use ode23 to solve the epidemic outbreak problem.
clear all
% Variables
k = 1e-5; % infectiousness of disease, per person per contact per day
gamma = 4; % recovery period, days
% Initial conditions
y0(1) = 100000;
y0(2) = 100;
y0(3) = 0;
% Time interval
tf = 100; % days
% Call ODE Solver
[t, y] = ode23(‘epidemic’, tf, y0, [], k, gamma);
MATLAB program 7.13
function f = epidemic(t, y, flag, k, gamma)
% Evaluate slope f(t,y) of coupled ODEs for dynamics of epidemic outbreak
% Constants
beta = 0.0001; % birth rate, per person per day
mu = 0.00001; % death rate, per person per day
f = [-k*y(1)*y(2) + beta*(y(1)+y(3)) - mu*y(1); ...
k*y(1)*y(2) - 1/gamma*y(2); ...
1/gamma*y(2) - mu*y(3)];
7.5 Multistep ODE solvers
The Euler and the RK methods of numerical ODE integ ration are called one-step
methods because they use the solution y
k
at the current time step t
k
to estimate the
solution at the next time step t
kþ1
. In RK methods, the formula to obtain the
numerical approximation to yt
kþ1
ðÞrequires evaluation of the slope at one or
more time points within the subinterval t
k
; t
kþ1
½over which integration is currently
being performed. Information on the solution prior to t
k
is not used to determine
y
kþ1
in these methods. Thus, in these methods the integration moves forward by
stepping from the current step to the next step, i.e. by a single step.
population succumbs to the disease. The disease however does not disappear, but remains embedded
in the population, even after 10 years.
Note that these models are highly simplified. The equations assume that each person has an equal
probability of coming into contact with another person. It has been found that some epidemic models
are better explained using complex network theory that uses a power law distribution to model the
number of people that an individual of a population comes into contact with. Complex network theory
assigns some people the status of “hubs.” Disease spreads most easily through “hubs” since they are
the most well-connected (Barabasi, 2003).
451
7.5 Multistep ODE solvers

Much useful information is contained in the solution at time points earlier than t
k
.
The change in the values of y
k
; y
k1
; y
k2
; ... at previous time points provides a
measure of the rate of change in the slope f
0
ðt; yÞ and higher derivatives of y. The
knowledge of prior solutions over a larger time interval consisting of severa l time
steps can be used to obtain more accurate app roximations to the solution at the next
time point. ODE integration methods that use not only the so lution at the current
step t
k
to approximate the solution at the next step, but also previous solution values
at t
k1
; t
k2
; ...are called multistep methods.
A general-purpose numerical integration formula for a three-step method is
y
kþ1
¼p
1
y
k
þ p
2
y
k1
þ p
3
y
k2
þ hq
0
ft
kþ1
; y
kþ1
ðÞþq
1
ft
k
; y
k
ðÞþq
2
ft
k1
; y
k1
ðÞþq
3
ft
k2
; y
k2
ðÞ½;
where p
1
; p
2
; p
3
; q
0
; q
1
; q
2
, and q
3
are constants that are derived using the Taylor
series.
One adv antage of multistep methods for ODE integration is that only one
evaluation of fðt; yÞ is required for each step regardless of the order of the method.
Function values at previous time points are already available from previous inte-
gration steps in the multistep method. However, multistep methods are not self-
starting, because several previous solution points are required by the formula to
calculate y
kþ1
. An initial condition, in most cases, consists of the value of y at one
initial time point only. To begin the integrati on, a one-step method of order equal to
that of the multistep method is used to generate the solution at the first few time
points, and after that the multistep method can take over.
There are two kinds of multistep methods: explicit methods and implicit methods.
Explicit multistep methods do not require an evaluation of the slope at t
kþ1
to find
y
kþ1
. Implicit multistep methods include a term for the slope at t
kþ1
on the right-
hand side of the integration formula. The implicit methods have better stability
properties, but are harder to execute than explicit methods. Unless the slope function
is linear in y, a nonlinear root-finding algori thm must be used to search for y
kþ1
.A
variety of multistep algorithms have been developed. We discuss the Adams methods
of explicit and implicit type for multistep ODE integration. MATLAB offers an
ODE solver based on an Adams routine.
7.5.1 Adams methods
The Adams–Bashforth methods are explicit multistep ODE integration schemes in
which the number of steps taken during the integration at each time step is equal to
the order of the method. Keep in mind that the order of a method is equal to the
order of the global truncation error produced by that method. The integration
formula for an m-step Adams–Bashforth method is given by
y
kþ1
¼ y
k
þ h
X
m
j¼1
q
j
ft
kjþ1
; y
kjþ1
: (7:44)
The formula for an m-step Adams–Bashforth method can be derived using the
Taylor seri es expansion about yt
k
ðÞwith step size h, as follows:
yt
kþ1
ðÞ¼yt
k
ðÞþft
k
; yt
k
ðÞðÞh þ
f
0
t
k
; yt
k
ðÞðÞh
2
2!
þ
f
00
t
k
; yt
k
ðÞðÞh
3
3!
þ Oh
4
:
452
Numerical integration of ODEs
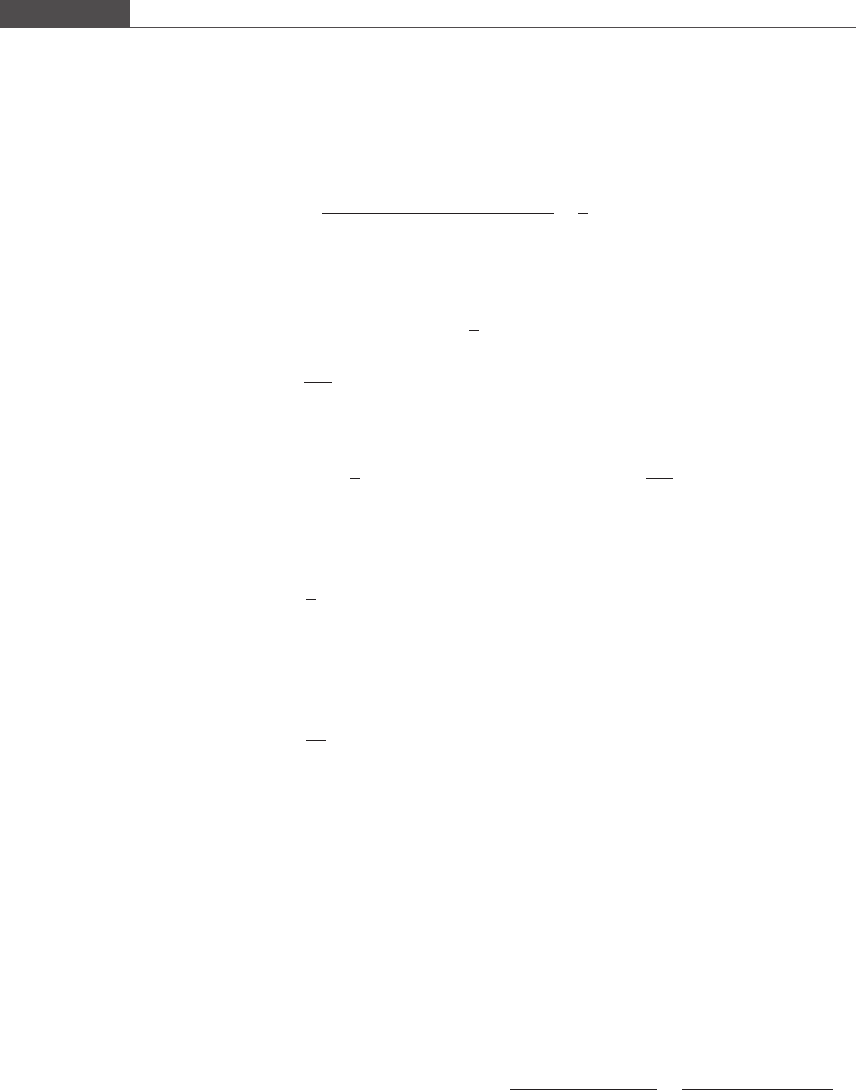
Substituting numerical differentiation formulas for derivatives of f generates a
multistep difference formula. This is demonstrated for a two-step Adams–
Bashforth method.
We can approximate the first derivative of f using the first-order backward differ-
ence formula (Equation (1.22)),
f
0
t
k
; yt
k
ðÞðÞ
ft
k
; yt
k
ðÞðÞft
k1
; yt
k1
ðÞðÞ
h
þ
h
2
f
00
t
k
; yt
k
ðÞðÞþOh
2
:
Substituting the backward difference formula above into the Taylor expansion,
we get
yt
kþ1
ðÞ¼yt
k
ðÞþft
k
; yt
k
ðÞðÞh þ
h
2
ft
k
; yt
k
ðÞðÞft
k1
; yt
k1
ðÞðÞðÞ
þ
5h
3
12
f
00
t
k
; yt
k
ðÞðÞþOh
4
:
This simplifies to
yt
kþ1
ðÞ¼yt
k
ðÞþ
h
2
3ft
k
; yt
k
ðÞðÞft
k1
; yt
k1
ðÞðÞðÞþ
5h
3
12
f
00
ξ; y ξðÞðÞ;
where ξ 2 t
k1
; t
kþ1
½. Writing ft
k
; yt
k
ðÞðÞas f
k
, the second-order Adams–Bashforth
formula is given by
y
kþ1
¼ y
k
þ
h
2
3f
k
f
k1
ðÞ: (7:45)
Upon substituting a second-order backward difference approximation for the first
derivative of f and a first-order backward difference formula for the second deriv-
ative of f, we obtain the third-order Adams–Bashforth formula:
y
kþ1
¼ y
k
þ
h
12
23f
k
16f
k1
þ 5f
k2
ðÞ: (7:46)
In this way, higher-order formulas for the Adams–Bashforth ODE solver can be
derived.
The Adams–Moulton methods are implicit multistep ODE integration schemes.
For these methods, the number of steps m taken to advance to the next time point is
one less than the order of the method. The integration formula for an m-step
Adams–Moulton method is given by
y
kþ1
¼ y
k
þ h
X
m
j¼0
q
j
ft
kþ1j
; y
kþ1j
: (7 :47)
The form ula for an m-step Adams–Moulton method can be derived using a Taylor
series expansion about yt
kþ1
ðÞwith step size −h, as follows:
yt
k
ðÞ¼yt
kþ1
ðÞft
kþ1
; yt
kþ1
ðÞðÞh þ
f
0
t
kþ1
; yt
kþ1
ðÞðÞh
2
2!
f
00
t
kþ1
; yt
kþ1
ðÞðÞh
3
3!
þ Oh
4
:
Substituting numerical differentiation formulas for derivatives of f generates a
multistep difference formula. Retaining only the first two terms on the right-hand
side, we recover Euler’s implicit method, a first-order method. Approximating the
first derivative of f in the Taylor series expansion with a first-order backward
453
7.5 Multistep ODE solvers

difference formula (Equation (1.22)), and dropping the Oh
3
terms, we obtain the
numerical integration formula for the modified Euler method, a secon d-order
method (see Section 7.2.3):
y
kþ1
¼ y
k
þ
1
2
f
k
þ f
kþ1
ðÞ: (7:48)
The associated Oh
3
error term is ðh
3
=12Þf
00
ξ; y ξðÞðÞ. Try to derive the error term
yourself.
Upon substituting a second-order backward difference approximation for the
first derivative of f and a first-order backward difference formula for the second
derivative of f, we obtain the third-order Adams–Moulton formula :
y
kþ1
¼ y
k
þ
h
12
5f
kþ1
þ 8f
k
f
k1
ðÞ: (7:49)
In this manner, higher-order formulas for the Adams–Moulton ODE solver can be
derived.
Upon comparing the magnitude of the error term of the second -order Adams–
Bashforth method and the second-or der Adams–Moulton method, we notice that
the local truncation error is smaller for the implicit Adams method. This is also the
case for higher-order explicit and implicit Adams methods. The smaller error lends
itself to smaller global truncation error and impro ved numerical stability.
Remember that instability of a numerical solution occurs when the error generated
at each step is magnified over successive time steps by the integration formula. The
second-order Adams–Moulton method is stable for all step sizes when the system of
ODEs is well-posed.
4
However, implicit multistep methods of order greater than 2
are not stable for all step sizes, and can produce truncation errors that grow without
bound when large step sizes are used (Grasselli and Pelinovsky, 2008).
7.5.2 Predictor–corrector methods
Implicit numerical ODE integration methods have superior stability characteristics
and smaller local truncation errors compared to explicit methods. However, execu-
tion of implicit methods can be cumbersome since an iterative root-finding algo-
rithm must be employed in general to find the solution at each time step. Also, to
begin the root- finding process, one must provide one or two guesses that lie close
to the true solution of the implicit ODE integration formula. Rather than having to
resort to iterative numerical methods for solving implicit multistep formulas, one
can obtain a prediction of the solution using the explicit multistep formula. The
explicit multistep ODE solver is called the predictor. The prediction y
ð0Þ
kþ1
is plugged
into the right-hand side of the implicit multistep ODE solver to calculate the slope at
ðt
kþ1
; y
ð0Þ
kþ1
Þ. The implicit formula imparts a correction on the prediction of the
solution made by the predictor. Therefore, the implicit ODE integration formula
is called the corrector.
Predictor and corrector formulas of the same order are paired with each other. An
example of a predictor–corrector pair is the second-order Adams–Bashforth method
paired with the second-order Adams–Moulton method shown below:
4
Well-posed ODEs have a unique solution that changes only slightly when the initial condition is
perturbed. An ODE whose solution fluctuates widely with small changes in the initial condition
constitutes an ill-posed problem.
454
Numerical integration of ODEs

predictor:
y
ð0Þ
kþ1
¼ y
k
þ
h
2
3f
k
f
k1
ðÞ;
corrector:
y
ð1Þ
kþ1
¼ y
k
þ
1
2
ðft
k
; y
k
ðÞþfðt
kþ1
; y
ð0Þ
kþ1
ÞÞ.
A numerical integration method that uses a predictor equation with error Oh
n
ðÞto
predict the solution and a corrector equation with error Oh
n
ðÞto improve upon the
solution is called a predictor–corrector method. In some predictor–corrector algo-
rithms, the corrector formula is applied once per time step and y
ð1Þ
kþ1
is used as the
final approximation of the solution at t
kþ1
. Alternatively, the approximation y
ð1Þ
kþ1
can be supplied back to the right-hand side of the corrector equation to obtain an
improved corrector approximation of the solution y
ð2Þ
kþ1
. This is analogous to per-
forming fixed-point iteration (see Chapter 5). Convergence of the corrector equation
is obtained when
y
ðiÞ
kþ1
y
ði1Þ
kþ1
y
ðiÞ
kþ1
E:
An advantage of the predictor–corrector algorithm is that it also provides an
estimate of the local truncation error at each time step. The exact solution at t
kþ1
can be expressed in terms of the predictor solut ion,
yt
kþ1
ðÞ¼y
ð0Þ
kþ1
þ c
1
h
nþ1
y
nþ1
ξ
1
ðÞ;
and the corrector solution as
yt
kþ1
ðÞ¼y
ðiÞ
kþ1
þ c
2
h
nþ1
y
nþ1
ξ
2
ðÞ:
By assuming that ξ
1
ξ
2
¼ ξ, we can subtract the two expressions above to get
y
ðiÞ
kþ1
y
ð0Þ
kþ1
¼ c
1
c
2
ðÞh
nþ1
y
nþ1
ξðÞ:
Simple algebraic manipulations yield
c
2
c
1
c
2
y
ðiÞ
kþ1
y
ð0Þ
kþ1
¼ c
2
h
nþ1
y
nþ1
ξðÞ: (7:50)
Thus, the approximations yielded by the predictor and corrector formulas allow us
to estimate the local truncation error at each time step. Specifically for the second-
order Adams–Bashforth–Moulton method:
c
1
¼
5
12
; c
2
¼
1
12
:
Thus, for the second-order predictor–corrector method based on Adams formulas,
the local truncation error at t
kþ1
can be estimated with the formula
1
6
y
ðiÞ
kþ1
y
ð0Þ
kþ1
:
As discussed in Section 7.4, local error estimates come in handy for optimizing the
time step such that the local error is always well within the tolerance limit. The local
truncation error given by Equation (7.50) can be compared with the tolerance limit
to determine if a change in step size is warranted. The condition imposed by the
tolerance limit E is given by c
2
h
nþ1
opt
y
nþ1
ξðÞE. Substituting y
nþ1
ξðÞE=c
2
h
nþ1
opt
into
Equation (7.50), we obtain, after some rearrangement,
455
7.5 Multistep ODE solvers
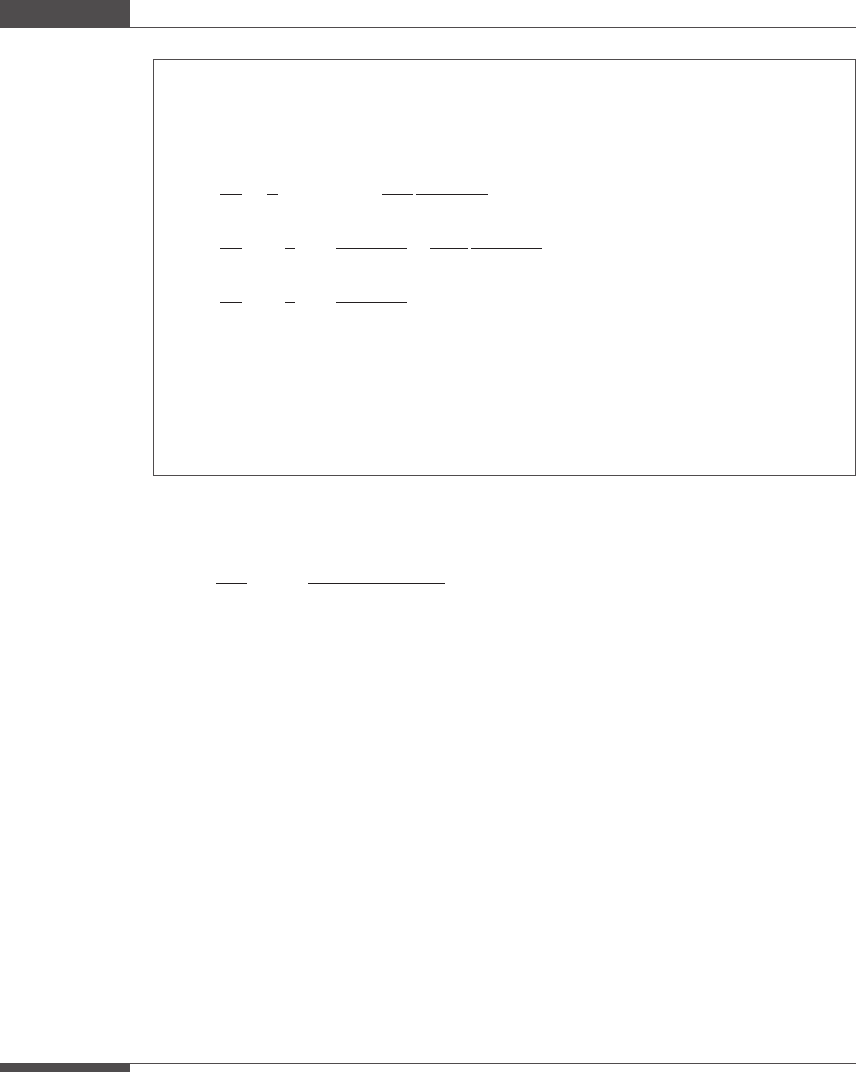
h
opt
h
nþ1
E c
1
c
2
ðÞ
c
2
y
ðiÞ
kþ1
y
ð0Þ
kþ1
: (7:51)
An adjustment to the step size requires recalculation of the solution at new, equally
spaced time points. For example, if the solutions at t
k
; t
k1
; and t
k2
are used to
calculate y
kþ1
, and if the time step is halved during the interval t
k
; t
kþ1
½, then, to
generate the approximation for y
kþ1=2
, the solutions at t
k
; t
k1=2
; and t
k1
are
required. Also, y
k1=2
must be determined using interpolation formulas of the
same order as the predictor–corrector method. Step size optimization for multistep
methods entails more computational work than for one-step methods.
Using MATLAB
The MATLAB ODE solver ode113 is based on the Adams–Bashforth–Moulton
method. This solver is preferred for problems with strict tolerance limits since the
multistep method on which the solver is based produces smaller local truncation
errors that the one-step RK method of corresponding order.
7.6 Stability and stiff equations
In earlier sections of this chapter, we discussed the stability properties of one-step
methods, specifically the Euler and explicit RK methods (implicit RK methods have
been devised but are not discussed in this book.) When solving a well-posed system
of ODEs, the ODE solver that yields a solution whose relative error is kept in control
even after a large number of steps is said to be numerically stable for that particular
problem. If the relative error of the solution at each time step is magnified at the next
time step, the numerical solution will diverge from the exact solution. The solution
Box 7.4B Microbial population dynamics
The coupled ODEs that describe predator–prey population dynamics in a mixed culture microbial
system are presented below after making the following substitutions: y
1
¼ S; y
2
¼ N
1
; y
3
¼ N
2
.
dy
1
dt
¼
F
V
y
1;0
y
1
1
Y
N
1
jS
μ
N
1
;max
y
1
y
2
K
N
1
þ y
1
;
dy
2
dt
¼
F
V
y
2
þ
μ
N
1
;max
y
1
y
2
K
N
1
þ y
1
1
Y
N
2
jN
1
μ
N
2
;max
y
2
y
3
K
N
2
þ y
2
;
dy
3
dt
¼
F
V
y
3
þ
μ
N
2
;max
y
2
y
3
K
N
2
þ y
2
:
Using the kinetic parameters that define the predator–prey system (Tsuchiya et al., 1972), we attempt to
solve this system of ODEs using ode113. However, the numerical algorithm is unstable and the
solution produced by the ODE solver diverges with time to infinity. For the given set of parameters, this
system of equations is difficult to integrate because of sudden changes in the substrate concentration
and microbial density with time. Such ODEs are called stiff differential equations, and are the topic of
Section 7.6.
456
Numerical integration of ODEs
