King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

Note the following properties of the roots of a Legendre polynomial that

are presented below without proof (see Grasselli and Pelinovs ky (2008) for proofs).

(1) The roots of a Legendre polynomial are simple, i.e. no multiple roots (two or more

roots that are equal) are encountered.

(2) All roots of a Legendre polynomial are located symmetrically about zero within the

interval ð1; 1Þ.

(3) No root is located at the endpoints of the interval. Thus, Gauss–Legendre quad-

rature is an open-interval method.

(4) For an odd number of nodes, zero is always a node.

Once the Legendre polynomial roots are speciﬁed, the weights of the quad-

rature formula can be calculated by integrating the Lagrange polynomials over

the interval. The weights of Gauss–Legendre quadrature formulas are always

positive. If the nodes were evenly spaced, this would not be the case. Tenth-

and higher-order Newton–Cotes formulas, i.e. formulas that use an eighth- or

higher-degree polynomial interpolant to approximate the integrand function,

have both positive and negative weights, which can lead to subtractive cancel-

lation of signiﬁcant digits and large round-off errors (see Chapter 1), under-

mining the accuracy of the method. Gauss–Legendre quadrature uses positive

weights at all times, and thus the danger of subtractive cancellation is

precluded.

The roots of the Legendre polynomials, and the corresponding weights, calcu-

lated using Equation (6.47) or by other means, have been extensively tabulated for

many values of n. Table 6.4 lists the Gauss–Legendre nodes and weights for

n ¼ 1; 2; 3; 4.

Table 6.4. Gauss–Legendre nodes and weights

Nodes, z

(roots of Legendre

polynomial Φ

nþ1

zðÞ) Weights, w

1 −0.5773502692

0.5773502692

1.0000000000

2 −0.7745966692

0.0000000000

0.7745966692

0.5555555556

0.8888888889

0.5555555556

3 −0.8611363116

−0.3399810436

0.3399810436

0.8611363116

0.3478548451

0.6521451549

0.3478548451

4 −0.9061798459

−0.5384693101

0.0000000000

0.5384693101

0.9061798459

0.2369268850

0.4786286705

0.5688888889

0.4786286705

0.2369268850

n is the degree of the polynomial interpolant

397

6.5 Gaussian quadrature

The nodes z

and weights w

are deﬁned on the interval ½1; 1. A simple trans-

formation shown earlier converts the integral from the original interval scale ½a; bto

½1; 1. Equation (6.45) is used to perform quadrature once the weights are

calculated.

The error associated with Gauss–Legendre quadrature is presented below with-

out proof (Ralston and Rabinowitz, 1978):

E ¼

2nþ3

ðn þ 1Þ!½

2n þ 3ðÞ2n þ 2ðÞ!½

ð2nþ2Þ

ξðÞ; ξ 2 a; b½:

Example 6.1

The nodes of the three-point Gauss–Legendre quadrature are 

ﬃﬃﬃﬃﬃﬃﬃﬃ

3=5

; 0;

ﬃﬃﬃﬃﬃﬃﬃﬃ

3=5

. Derive the

corresponding weights by integrating the Lagrange polynomials according to Equation (6.47).

We have

1

∏

j¼1;2

z  z



 z



1

z  0ðÞz 

ﬃﬃ





ﬃﬃ

 0





ﬃﬃ



ﬃﬃ



1



ﬃﬃﬃ



ﬃﬃﬃ

1

;

Similarly, one can show that w

¼ 8=9 and w

¼ 5=9.

Example 6.2

Use the two-point and three-point Gauss–Legendre rule and Simpson’s 1/3 rule to calculate the cumulative

standard normal probability,

ﬃﬃﬃﬃﬃ

2π

2

x

dx:

The integrand is the density function (Equation (3.32); see Chapter 3 for details) that describes the

standard normal distribution. Note that x is a normal variable with a mean of zero and a standard deviation

equal to one.

The exact value of the integral to eight decimal places is

2

x

dx ¼ 2:39257603:

The integration limits are a ¼2 and b ¼ 2. Let x ¼ 2z, where z is defined on the interval ½1; 1.

Using Equation (6.44),

Here, z stands for a variable of integration with integration limits −1 and 1. In this example, x is the

standard normal variable, not z.

398

Numerical quadrature

2

x

dx ¼ 2

1

2z

dz:

According to Equation (6.45), Gauss–Legendre quadrature gives us

2

x

dx  2

i¼0

2z

For n =1,z

0;1

¼1=

ﬃﬃﬃ

; w

0;1

¼ 1:0, and

n ¼ 2; z

0;2

¼

ﬃﬃﬃﬃﬃﬃﬃﬃ

3=5

; z

¼ 0:0; w

0;2

¼ 5=9; w

¼ 8=9.

Two-point Gauss–Legendre quadrature yields

2

x

dx  22 e

2z



¼ 2:05366848;

with an error of 14.16%.

Three-point Gauss–Legendre quadrature yields

2

x

dx  22

2z



¼ 2:44709825;

with an error of 2.28%.

Simpson’s 1/3 rule gives us

2

x

dx 

ð2Þ

þ 4e

0

þ e

2



¼ 2:84711371

with an error of 19.0%.

The two-point quadrature method has a slightly smaller error than Simpson’s 1/3 rule. The latter requires

three function evaluations, i.e. one additional function evaluation than that required by the two-point

Gauss–Legendre rule. The three-point Gauss–Legendre formula has an error that is an order of magnitude

smaller than the error of Simpson’ s 1/3 r ule.

To improve accuracy further, the integration interval can be split into a number

of smaller intervals, and the Gauss–Legendre quadrature rule (Equation (6.45)

with nodes and weights given by Table 6.4) can be applied to each subinterval.

The subintervals may be chosen to be of equal width or of differing widths. When

the Gaussian quadrature rule is applied individually to each subinterval of the

integration interval, the quadrature scheme is called composite Gaussian quadrature.

Suppose the interval ½a; b is divided into N subintervals of equal width equal to d,

where

d ¼

b  a

Let n be the degree of the polynomial interpolant so that there are n + 1 nodes within

each subinterval and a total of n þ 1ðÞN nodes in the entire interval. The Gauss–

Legendre quadrature rule requires that the integration limits x

i1

; x

½of any sub-

interval be transform ed to the interval ½1; 1. The weighted summation formula

applied to each subinterval is

i1

fxðÞdx ¼

1

z þ x

ði0:5Þ



dz 

k¼0

þ x

ði0:5Þ



; (6:49)

where x

ði0:5Þ

is the midpoint of the ith subinterval. The midpoint can be

calculated a s

399

6.5 Gaussian quadrature

i0:5ðÞ

i1

þ x

i0:5ðÞ

¼ x

þ di



The numerical approximation of the integral over the entire interval is equal to the

sum of the individual approximations:

fxðÞdx ¼

fxðÞdx þ

fxðÞdx þþ

N1

fxðÞdx;

fxðÞdx 

i¼N

i¼1

k¼0

þ x

ði0:5Þ



: (6:50)

Equation (6.50) can be automa ted by writing a MATLAB program, as demonstra-

ted in Program 6.6. While the nodes and weights listed in the program correspond to

the two-point quadrature scheme, nodes and weights for higher precision (n + 1)-

point Gauss–Legendre quadrature formulas can be also incorporated in the pro-

gram (or as a separate program that serves as a look-up table). By includi ng the value

of n as an input parameter, one can select the appropriate set of nodes and weights

for quadrature calculations.

MATLAB program 6.6

function I = composite GLrule(integrandfunc, a, b, N)

% This function uses the composite 2-point Gauss-Legendre rule to

% approximate the integral.

% Input variables

% integrandfunc : function that calculates the integrand

% a : lower limit of integration

% b : upper limit of integration

% N : number of subintervals

% Output variables

% I : value of integral

% Initializing

I=0;

% 2-point Gauss-Legendre nodes and weights

z(1) = -0.5773502692; z(2) = 0.5773502692;

w(1) = 1.0; w(2) = 1.0;

% Width of subintervals

d = (b-a)/N;

% Mid-points of subintervals

xmid = [a + d/2:d:b - d/2];

400

Numerical quadrature

% Quadrature calculations

for i = 1: N

% Nodes in integration subinterval

x = xmid(i) + z*d/2;

% Function evaluations at node points

y = feval(integrandfunc, x);

% Integral approximation for subinterval i

I = I + d/2*(w*y’); % term in bracket is a dot product

end

Example 6.3

Use the two-point Gauss–Legendre rule and N = 2, 3, and 4 subintervals to calculate the following integral:

2

x

dx:

The exact value of the integral to eight decimal places is

2

x

dz ¼ 2:39257603:

The integration limits are a ¼2 and b ¼ 2. This integral is solved using Program 6.6. A MATLAB

function is written to evaluate the integrand.

MATLAB program 6.7

function f = stdnormaldensity(x)

% This function calculates the density function for the standard normal

% distribution.

f = exp(-(x.^2)/2);

The results are given in Table 6.5.

The number of subintervals required by the composite trapezoidal rule to achieve an accuracy of

0.007% is approximately 65.

The Gaussian quadrature method is well-suited for the integration of functions

whose analytical form is known, so that the function is free to be evaluated at any

point within the interval. It is usually not the method of choice when discrete

values of the function to be integrated are available, in the form of tabulated

data.

Table 6.5. Estimat e of integral using composite

Gaussian quadrature

NI Error (%)

2 2.40556055 0.543

3 2.39319351 0.026

4 2.39274171 0.007

401

6.5 Gaussian quadrature

Using MATLAB

The MATLAB function quadl performs numerical quadrature using a four-point

adaptive Gaussian quadrature scheme called Gauss–Lobatto. The syntax for quadl

is the same as that for the MATLAB function quad.

6.6 End of Chapter 6: key points to consider

(1) Quadrature refers to use of numerical methods to solve an integral. The integrand

function is approximated by an interpolating polynomial function. Integration of

the polynomi al interpolant produces the following quadrature formula:

fðxÞdx 

i¼0

fðxÞ; a  x

 b:

(2) An interpolating polynomia l function,orpolynomial interpolant, can be constructed

by several means, such as the Vandermonde matrix method or using Lagrange

interpolation formulas.

(3) The Lagrange interpolation formula for the nth-degree polynomial pðxÞ is

pxðÞ¼

k¼0

∏

j¼0;j6¼k

x  x



 x



k¼0

;

where L

are the Lagrange polynomials.

(4) If the function values at both endpoints of the interval are included in the quadrature

formula, the quadrature method is a closed method; otherwise the quadrature

method is an open method.

(5) Newton–Cotes integration formulas are derived by approximating the integrand

function with a polynomial function of degree n that is constructed from function

values obtained at equally spaced nodes.

(6) The trapezoidal rule is a closed Newton–Cotes integration formula that uses a ﬁrst-

degree polynomial (straight line) to approximate the integrand functi on. The tra-

pezoidal formula is

fxðÞdx 

ðÞþfx

ðÞðÞ:

The composite trapezoidal rule uses a piecewise linear polynomial to approximate

the integrand function over an interval divided into n segments. The degree of

precision of the trapezoidal rule is 1. The error of the composite trapezoidal rule is



(7) Simpson’s 1/3 rule is a closed Newton–Cotes integration formula that uses a second-

degree polynomial to approximate the integrand function. Simpson’s 1/3 formula is

fxðÞdx 

ðÞþ4fx

ðÞþfx

ðÞðÞ:

The composite Simpson’s 1/3 rule uses a piecewise quadratic polynomial to approx-

imate the integrand function over an interval divided into n segments. The degree of

precision of Simpson’s 1/3 rule is 3. The error of compo site Simpson’s 1/3 rule is



402

Numerical quadrature

(8) Simpson’s 3/8 rule is a Newton–Cotes closed integration formula that uses a cubic

interpolating polynomial to approximate the integrand function. The formula is

fxðÞdx 

ðÞþ3fx

ðÞþfx

ðÞðÞ:

The error associ ated with basic Simpson’s 3/8 rule is Oh



, which is of the same

order as basic Simps on’s 1/3 rule. The degree of precision of Simpson’s 3/8 rule is 3.

The composite rule has a truncation error of Oh



(9) Richardson’s extrap olation is a numerical scheme used to combine two numerical

approximations of lower order in such a way as to obtain a result of higher-

order accuracy. Romberg integration is an algorithm that uses Richardson’s extrap-

olation to improve the accuracy of numerical integration. The trapez oidal rule is

used to generate mOh



approximations of the integral using a step size that

doubles with each successive approxim ation. The approximations are then com-

bined pairwise to obtain (m − 1) Oh



second-level approximations. The (m − 2)

third-level Oh



approximations are computed from the second-level approxima-

tions. This process continues until the mth level approximation is attained or a user-

speciﬁed tolerance is met.

(10) Gaussian quadrature uses an nth-degree polynomial interpolant of the integrand

function to achieve a degree of precision equal to 2n + 1. This method optimizes the

location of the n + 1 nodes within the interval as well as the n + 1 weights. The node

points of the Gauss–Legendre quadrature method are the roots of the Legendre

polynomial of degree n + 1. Gauss–Legendre quadrature is an open-interval

method. The roots are all located symmetrically in the interior of the interva l.

Gaussian quadrature is well suited for numerical integration of analytical functions.

6.7 Problems

6.1. Transport of nutrients to cells suspen ded in cell culture media For the problem

stated in Box 6.2, construct a piecewise cubic interpolating polynomial to approx-

imate the solute/drug concentration proﬁle near the cell surface for t = 40 s. Plot the

approximate concentration proﬁle. How well does the interpolating function

approximate the exact function? Compare your plot to Figure 6.8, which shows

the concentration proﬁle for t = 10 s. Explain in a qualitative sense how the shape of

the concentration proﬁle changes with time.

6.2. You were introduced to the following error function in Box 6.2:

erfðzÞ¼

ﬃﬃﬃ

z

dz:

Use the built-in MATLAB function quad to calculate erfðzÞ and plot it for z ∈

[−4, 4]. Then calculate the error between your quadrature approximation and the

built-in MATLAB function erf. Plot the error between your quadrature approxi-

mation and the “correct” value of erfðzÞ. Over which range is the quadrature scheme

most accurate, and why?

6.3. Use the composite Simpson’s 1/3 rule to evaluate numerically the following deﬁnite

integral for n = 8, 16, 32, 64, and 128:

3 þ 5xðÞx

þ 49ðÞ

403

6.7 Problems

Compare your results to the exact value as calculated by evaluating the analytical

solution, given by

3 þ 5xðÞ7

þ x

ðÞ

þ 7

ðÞ

5  log 3 þ 5x



log 7

þx



tan

1



at the two integration limits.

The error scales with the inverse of n raised to some power as follows:

error 

If you plot the log of error versus the log of the number of nodes, N, the slope of a

best-ﬁt line will be equal to − α:

logðerrorÞ¼α log n þ C:

Construct this plot and determine the slope from a polyﬁt regression. Determine

the value of the order of the rule, α. (Hint: You can use the MATLAB plotting

function loglog to plot the error with respect to n.)

6.4. Pharmacodynamic analysis of morphine effects on ventilatory response to

hypoxia Researchers in the Department of Anesthesiology at the University of

Rochester studied the effects of intrathecal morphine on the ventilatory response to

hypoxia (Bailey et al., 2000). The term “intrathecal” refers to the direct introduction

of the drug into the sub-arachnoid membrane space of the spinal cord. They

measured the following time response of minute ventilation (l/min) for placebo,

intravenous morphine, and intrathecal morphi ne treatments. Results are given in

Table P6.1.

One method of reporting these results is to compute the “overall effect,” which is

the area under the curve divided by the total time interval (i.e. the time-weighted

average). Compute the overall effect for placebo, intravenous, and intrathecal

morphine treatments using (i) the trapezoidal quadrature method, and (ii)

Simpson’s 1/3 method. Note that you should separate the integral into two different

intervals, since from t =0−2 hours the panel width is 1 hour and from 2–12 hours

the panel width is 2 hours.

Bailey et al. (2000) obtained the values shown in Table P6.2. How do your results

compare to those given in that table ?

Table P6.1. Minute ventilation (l/min)

Hours Placebo Intravenous Intrathecal

038 34 30

1 35 19 23.5

242 16 20

4 35.5 16 13.5

635 17 10

8 34.5 20 11

10 37.5 24 13

12 41 30 19.5

404

Numerical quadrature

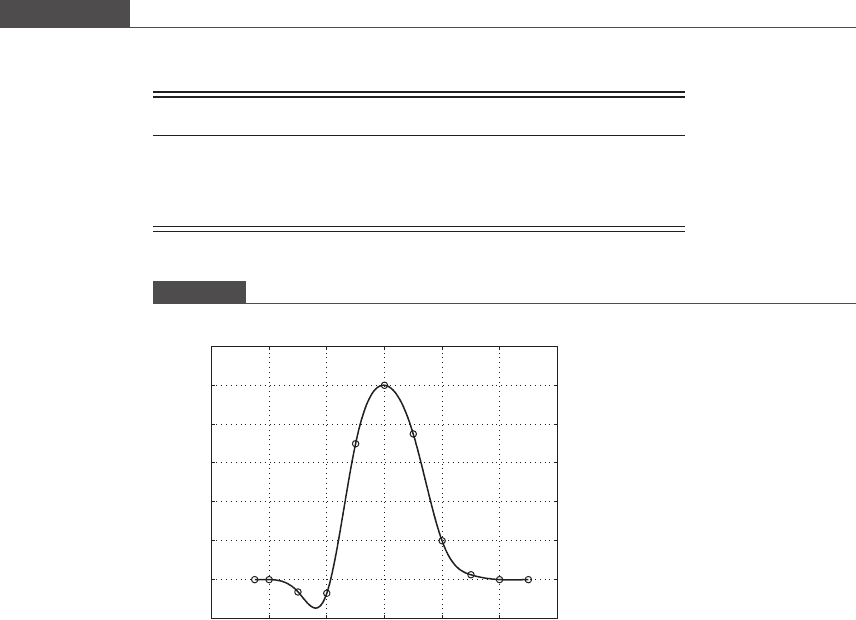
6.5. MRI imaging in children and adults Functional MRI imaging is a non-invasive

method to image brain function. In a study by Richter and Richter (2003), the

brain’s response was measured followi ng an impulse of visual stimulus. The readout

of these experiments was a variable called “T2*,” which represents a time constant

for magnetic spin recovery. The experiments were carried out in a 3T Siemens

Allegra Head Scanner, and the subject was shown a ﬂickering checkerboard for

500 ms at a frequency of 8 Hz. The aim of the study was to look for differences in the

temporal response between adults and children. Figure P6.1 resembles a typical

measurement. The data upon which the plot is based are given in Table P6.3.

Such curves are characterized by calculating the area under the curve. Using

Simpson’s 1/3 rule, calculate, by hand, the following integral:

I ¼



dt:

Since some of the area lies below the x-axi s, this area will be subtracted from the

positive area.

6.6. Polymer cyclization (Jacobs on–Stockmayer theory) Polymer chains sample a

large number of different orientations in space and time. The motion of a polymer

chain is governed by stochastic (probabilistic) processes. Sometimes, the two ends of

a linear polymer chain can approach each other within a reactive distance. If a bond

forms between the two polymer ends, the reaction is termed as cyclization.By

studying the probability with which this occurs one can estimate the rate at which

Table P6.2. Time-weighted average of minute ventilation (l/min)

Group Overall effect

Placebo 36.8 ± 19.2

Intravenous morphine 20.2 ± 10.8

Intrathecal morphine 14.5 ± 6.4

Figure P6.1

−2 0 2 4 6 8 10

−0.2

0.2

0.4

0.6

0.8

Time after stimulus onset (s)

T2* (arbitrary units)

405

6.7 Problems

a linear chain is converted to a circular chain. Consider a linear polymer with N links.

The probability that the two ends of the chain come within a bond distance b of each

other is given by the following integral:

2πNb



3=2

exp 3r

=2Nb



4πr

dr:

If N = 20 links and b = 1, calculate the probability the chain ends come within a

distance b of each other. Use a two-segment composite trapezoidal rule and then a four-

segment composite trapezoidal rule. Use these two approximations to extrapolate to an

even more accurate solution by eliminating the O(h

) error term, where h is the panel

width. You may perform these calculations either by hand or by writing one or more

MATLAB programs to evaluate the function and carry out trapezoidal integration.

6.7. Numerical quadrature of AFM data An atomic force microscope is used to probe

the mechanics of an endothelial cell surface. The data in Table P6.4 are collected by

measuring the cantilever force during a linear impingement experiment.

Calculate the integral of these data using composite Simpson’s 1/3 rule to obtain

the work done on the cell surface. Express your answer in joules.

6.8. Numerical quadrature and pharmacokinetics In the ﬁeld of pharmacokinetics, the

area under the curve (AUC) is the area under the curve in a plot of concentration of

drug in plasma against time. In real-world terms the AUC represents the total amount

Table P6.3. Experimental data set

t (s) T2*

−0.5 0

1 −0.063

2 −0.070

3 0.700

4 1.00

5 0.750

6 0.200

7 0.025

Table 6.4. AFM data set

Displacement (nm) Force (nN)

10 1.2

30 1.4

50 2.1

70 5.3

90 8.6

406

Numerical quadrature