King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

function values may not be available in the data set. Accordingly, two schemes of

numerical integration have been developed: open integration and closed integration.

The midpoint rule and Gaussian quadrature are examples of open integration

methods, in which evaluation of both endpoint function values of the interval is

not required to obtain the integral ap proximation. The trapezoidal rule and

Simpson’s rule use function values at both endpoints of the integration interval,

and are examples of closed integration formulas.

Box 6.1A Solute transport through a porous membrane

Solute transport through a porous membrane separating two isolated compartments occurs in a variety of

settings such as (1) diffusion of hydrophilic solutes (e.g. protein molecules, glucose, nucleic acids, and

certain drug compounds) found in the extracellular matrix into a cell through aqueous pores in the cell

membrane, (2) movement of solutes present in blood into the extravascular space through slit pores

between adjacent endothelial cells in the capillary wall, (3) membrane separation to separate particles of

different size or ultrafiltration operations to purify water, and (4) chromatographic separation processes.

Solute particles travel through the pores within the porous layer by diffusion down a concentration gradient

and/or by convective transport due to pressure-driven flow. The pore shape can be straight or convoluted.

Pores may interconnect with each other, or have dead-ends. When the solute particle size is of the same

order of magnitude as the pore radius, particles experience considerable resistance to entry into and

movement within the pore. Frictional resistance, steric effects, and electrostatic repulsive forces can slow

down or even preclude solute transport through the pores, depending on the properties and size of the

solute particles and the pores. Since a porous membrane acts as a selective barrier to diffusion or

permeation, the movement of solute through pores of comparable size is called hindered transport.

Mathematical modeling of the solute transport rate through a porous membrane is of great utility in

(1) developing physiological models of capillary (blood vessel) filtration, (2) studying drug transport in

the body, and (3) designing bioseparation and protein purification methods. The simplest model of

hydrodynamic (pressure-driven) and/or diffusive (concentration gradient-driven) flow of solute particles

through pores is that of a rigid sphere flowing in Stokes flow through a cylindrical pore. The hindered

transport model discussed in this Box was developed by Anderson and Quinn (1974), Brenner and

Gaydos (1977), and Smith and Deen (1983). A review is provided by Deen (1987).

Consider the steady state transport of a solid, rigid sphere of radius a flowing thro ugh a cylindrical pore of

radius R

and length L. The pore walls are impermeable and non-reactive. The sphere has a time-averaged

uniform velocity U in the direction of flow along length L (see Figure 6.3). The time-averaging smoothens

out the fluctuations in velocity due to the Brownian motion of the particle. Each cylindrical pore in the porous

membrane connects a liquid reservoir with solute concentration C

on one side of the membrane to another

liquid r eservoir of concentration C

that lies on the opposite side of the membrane (C

> C

). Let Cðr; zÞbe

the concentration (number of sphere centers per unit volume) of the solute in the pore. Particle motion

in the pore is due to convective fluid flow as well as diffusion down a concentration gradient.

The radius of the particle is made dimensionless with respect to the pore radius, α ¼ a=R

. The

dimensionless radial position of the particle in the pore is given by β ¼ r=R

Figure 6.3

Solute transport through a cylindrical pore.

357

6.1 Introduction

The flow within the pore is fully developed and the flow profile is parabolic, i.e. the fluid velocity is a

function of radial position only:

v βðÞ¼v

1  β



Fluid flow within the pores is at very low Reynolds number (Stokes flow or viscous flow). A freely

flowing suspended sphere in a bounded medium has a par ticle flow velocity equal to Gv, where G <1

and is called the “lag coefficient.” Note that G characterizes the reduction in particle velocity with

respect to fluid velocity due to resistance posed by the pore wall. Due to the concentration gradient

(chemical potential gradient), which is the driving force for diffusion, on average, the solute particles are

transported faster across the pore than the fluid itself. Since the sphere moves at an average velocity U

that is larger than Gv, it is not freely suspended in the fluid, and its expedient motion relative to the fluid

is retarded by wall friction. The drag force experienced by the sphere in Stokes flow is 6πμaKðU  GvÞ,

where K is the “enhanced drag” (Anderson and Quinn, 1974).

At steady state, the drag forces that act to oppose motion of the sphere relative to the fluid can be

equated to the chemical driving forces that induce motion of the sphere relative to the fluid. On doing so,

we arrive at the equation for solute flux N (quantity transported/cross-sectional area/time).

NðrÞ¼DK

1

∂C

∂z

þ GvC:

At steady state, the flux is only a function of radial position and does not depend on axial position z.

The average flux



N is obtained by averaging NðrÞ over the pore cross-sectional area. Solute concen-

tration C in the pore is a function of radial and axial position:

C ¼ gzðÞexp EðβÞ=kT½; (6:3)

where E is the potential energy of interaction between the sphere and the pore wall, k is the Boltzmann

constant, and T is the temperature. An example of interaction between the sphere and the por e wall is

electrostatic repulsion/attraction, which is observed when the surfaces have a net charge. Another

example is steric interaction, which arises due to the finite size α of the solute particles. The annular region

adjacent to the pore wall, defined as 1  α

r  1, is devoid of the centers of moving spheres. In other

words, the concentration of sphere centers in this region is zero. There is no solute flux at r

1  α.

We simplify the analysis by considering only diffusional transport of the solute, i.e. fluid velocity

v = 0. The average flux is as follows:



N ¼

1α

N 2πβðÞdβ

2πβðÞdβ

¼2D

1α

1

ðβÞexp E ðβÞ=kT½β d β: (6:4)

The concentration



CðzÞ averaged over the cross-sectional area is obtained by integrating

Equation (6.3):

π  1

1α

C 2πβðÞdβ ¼



C ¼ g

1α

exp EðβÞ=kT½2βðÞdβ:

Taking the derivative with respect to z, we obtain an expression for ∂g=∂z:



C=dz

1α

exp EðβÞ=kT½2βðÞdβ

: (6:5)

Substituting this relationship into Equation (6.4), we get



N ¼DK



;

where (Brenner and Gaydos, 1977)

¼ K

1

1α

1

exp EðβÞ=kT½β dβ

1α

exp EðβÞ=kT½β dβ

: (6 :6)

358

Numerical quadrature

During steady state diffusion, the cross-sectional average concentration



C is a linear function of the

distance traveled along the pore,



C ¼











 z;

and



¼







The bulk solute concentration immediately outside the pore at z =0,L is not equal to the average

solute concentration



CðzÞ just inside the pore. This is because steric and electrostatic interactions

influence the distribution of solute within the pore such that the concentration within the pore may be

less or more than the external concentration. If only steric interactions are present, a lower concentration

of solute particles will be present in the pore at z = 0 than outside the pore. In this case, the

concentration profile in the pore at z = 0 is given by

CðβÞj

z¼0

β  1  α

0 β

1  α:



The partition coefficient Φ is the ratio of the average internal pore concentration to the external

concentration of solute in the bulk solution at equilibrium:

Φ ¼



1α

 exp EðβÞ=kT½2πβ dβ

π  1

ðÞ

¼ 2

1α

exp EðβÞ=kT½β dβ: (6:7)

The concentration gradient in the pore can be expressed in terms of the outside pore solute concen-

trations and the partition coefficient:



¼Φ

 C

Thus, the steady-state cross-sectional average solute flux is given by



N ¼ ΦDK

 C



Smi th and Deen (1983) calculated the interaction energy EðβÞ between a sphere and

the pore wall, both with constant surface charge density, as a function of the sphere position in the

pore. The solvent was assumed to be a 1 : 1 univalent electrolyte (e.g. NaCl, KCl, NaOH, or KBr

solution).

When a charged surface (e.g. negatively charged) is placed in an electrolytic solution, the counter-

ions (positive ions) in the solution distribute such that they exist at a relatively higher concentration near

the charged surface due to electrostatic attraction. A “double layer” of charge develops on each charged

surface, and consists of the surface charge layer and the accumulated counter-charges adjacent to the

surface. The thickness of the double layer depends on the concentration of the ions in the solution and

the valency of each ion species in the solution. The counter-ions that assemble near the charged surface

tend to screen the electrostatic effects of the charged surface. As the ionic strength of the solution

decreases (concentration of salt is reduced) the counter-ion screening of the surface charges weakens

and the double layer width increases.

The Debye length (1=κÞ can be viewed as the thickness of the electric double layer. It is strictly a

property of the solvent. A large magnitude indicates that the charges on the surface are not well shielded

by counter-ions present in the solution. On the other hand, a narrow double layer results when a large

concentration of counter-ions adjacent to the surface charge shields the charges on the surface

effectively. As the Debye length increases, the double layers of two closely situated charged surfaces

interact more strongly with each other.

359

6.1 Introduction

The interaction energy EðβÞ in Equation (6.3) is equal to

(Smith and Deen, 1983)

E βðÞ¼R



ΔG; (6:8)

where ΔG is the dimensionless change in free energy that occurs when the sphere and pore are brought

from infinite separation to their interacting position.

The physical constants are as follows:

F = Faraday constant = 96485.34 C/mol,

R = gas constant = 8.314 J/(mol K)

k = Boltzmann constant = 1.38 × 10

−23

J/(molecule/ K),

= dielectric permittivity of free space = 8.8542 × 10

−12

C/(V m),

ε = relative permittivity, i.e. the ratio of solvent dielectric permittivity to permittivity in a vacuum.

For constant surface charge densities q

at the pore wall, and q

at the sphere surface, ΔG for the

system is given by (Smith and Deen, 1983)

ΔG ¼

8πτα

τα

1þταðÞ

 Λσ

4π

ðτβÞ

1þταðÞI

ðτÞ

 σ

πI

ðτβÞ

τI

ðτÞ





τα

 e

τα

ðÞταL ταðÞ

1 þ ταðÞ



 σ

πτ e

τα



2 e

τα

e

τα

ðÞταL ταðÞΛ

1þταðÞ

; (6:9)

where

is the dimensionless sphere surface charge density,

is the dimensionless cylinder surface charge density,

and K

are the modified Bessel functions of order ν,

L ταðÞ¼coth τα ð1=ταÞ,

Λ ﬃ

τβðÞ

∞

t¼0

2tðÞ!

t!ðÞ

τβðÞτK

tþ1

2τðÞþ0:75K

2τðÞ½

;

τ ¼ R

κ ¼ R

electrolyte;∞

1=2

, is the ratio of the pore radius R

to the Debye length 1=κ,

electrolyte;∞

= bulk concentration of electrolyte,

= valency of ion species (i = 1 for both the positive and negative ions that constitute the 1 : 1

univalent electrolyte).

The parameters for this system are:

= 0.01 C/m

ε = 74 for a dilute 1 : 1 univalent aqueous solution,

T = 310 K,

electrolyte,∞

= 0.01 M,

= 20 nm,

α = 0.25.

You are asked to calculate the partition coefficient Φ for the solute. To perform this task, one must

use numerical integration (Smith and Deen, 1983). The solution is demonstrated in Section 6.3 using

the trapezoidal rule and Simpson’s 1/3 rule.

The model makes the following assumptions.

(1) The solute concentration is sufﬁciently dilute such that no solute–solute electrostatic and hydro-

dynamic interactions occur. Therefore, we can model the motion of one sphere independently from

the motion of other spheres.

360

Numerical quadrature

Section 6.3 discusses the Newton–Cotes rules of integration, which include popular

methods such as the trapezoidal rule, Simpson’s 1/3 rule, and Simpson’s 3/8 rule.

The composite Newton–Cotes rules approximate the functional form of the inte-

grand with a piecewise polynomial interpolant. The interval is divided into

n subintervals of equal width. The truncation errors associated with the quadrature

algorithms are also derived. A convenient algorithm to impr ove the accuracy of the

trapezoidal rule by several orders of magnitude is Romberg integration, and is

considered in Section 6.4. Gauss–Legendre quadrature is a high accuracy method

of quadrature for integrating functions. The nodes at which the integrand function is

evaluated are the zeros of special orthogonal polynomials called Legendre polyno-

mials. Section 6.5 covers the topic of Gaussian quadrature. Before we discuss some

of the established numerical methods of integration, we start by introducing some

important concepts in polynomial interpolation and speciﬁcally the Lagrange

method of interpolation. The latter is used to develop the Newton–Cotes rules for

numerical integration.

6.2 Polynomial interpolation

Many scientiﬁc and industrial experiments produce discrete data sets, i.e. tabula-

tions of some measured value of a material or system property that is a function of a

controllable variable (the indepen dent variable). Steam tables, which list the ther-

modynamic properties of steam as a function of temperature and pressure, are an

example of a discrete data set. To obtain steam properties at any temperature T and/

or pressure P intermediate to those listed in the published tables, i.e. at T 6¼ T

, one

must interpolate tabulated values that bracket the desired value. Before we can

perform interpolation, we must deﬁne a function that adequately describes the

behavior of the steam property data subset. In other words, to interpolate the data

points, we must ﬁrst draw a smooth and continuous curve that joins the data points.

Often, a simple method like linear interpolation sufﬁces when the adjacent data

points that bracket the desired data point are close to each other in value.

Interpolation is a technique to estimate the value of a function fðxÞ at some value x, when the only

information available is a discrete data set that tabulates fðx

Þ at several values of x

, such that

a  x

 b, a

b; and x 6¼ x

Interpolation can be contrasted with extrapolation. The latter describes the process

of predicting the value of a function when x lies outside the interval over which the

measurements have been taken. Extrapolated values are pr edictions made using an

interpolation function and should be regarded with caution.

To perform interpolation, a curve, called an interpolating function, is ﬁtted to the

data such that the function passes through each data point. An interpolating function

(also called an interpolant) is used for curve ﬁtting of data when the data points are

accurately known. If the data are accompanied by a good deal of uncertainty, there is

little merit in forcing the function to pass through each data point. When the data are

error-prone, and there are more data points than undetermined equation parameters

(2) The pore length is sufﬁciently long to justiﬁably neglect entrance and exit effects on the velocity

proﬁle and to allow the particle to sample all possible radial positions within the pore.

(3) The electrical potentials are sufﬁciently small for the Debye–Hu

ckel form of the Poisson–Boltzmann

equation to apply (Smith and Deen, 1983).

361

6.2 Polynomial interpolation

(the unknowns in the interpolant), linear least-squares regression techniques are

used to generate a function that models the trend in the data (see Chapter 2 for a

discussion on linear least -squares regression).

Sometimes, a complicated functional dependency of a physical or material prop-

erty on an independent variable x is already established. However, evaluation of the

function fxðÞmay be difﬁcult because of the complexity of the functional form and/

or number of terms in the equation. In these cases, we search for a simple function

that exactly agrees with the true, complex function at certain points within the

deﬁned inter val of x values. The techniques of interpolation can be used to obtain

a simple interpolating function, in place of a complicated function, that can be used

quickly and easily.

Interpolating functions can be constructed using polynomials, trigonometric

functions, or exponential functions. We concentrate our efforts on polynomial

interpolation functions. Polynomials are a class of functions that are commonly

used to approximate a function. There are a number of advantages to using

polynomial functions to create interpolants: (1) arithmetic manipulation of poly-

nomials (addition, subtraction, multiplication, and division) is straightforward

and easy to f ollow, a nd (2) polynomials are e asy to d iffe re ntiat e and i ntegra te,

and the result of either procedure is still a polynomial. For these reasons, poly-

nomial interpolants have been used to develop a number of popular numerical

integration schemes.

A generalized polynomial in x of degree n contains n þ 1 coefﬁcients, and is as

follows:

pxðÞ¼c

þ c

n1

þ c

n2

þþc

x þ c

: (6:10)

To construct a polynomial of degree n, one must specify n + 1 points x; yðÞthat lie

on the path of pxðÞ. The n + 1 points are used to determine the values of the n +1

unknown coefﬁcients. For example, to generate a line, one needs to specify only two

distinct points that lie on the line. To generate a quadratic function, three different

points on the curve must be spe ciﬁed.

Only one polynomial of degree n exists that passes through any unique set of n + 1 points. In other

words, an interpolating polynomial function of degree n that is fitted to n + 1 data points is unique.

The above statement can be proven as follows. Suppose two different polynomials

pðxÞ and qðxÞ, both of degree n, pass through the same n + 1 points. If

rxðÞ¼pxðÞqðxÞ, then rðxÞ must also be a polynomial of degree either n or less.

Now, the difference pxðÞqðxÞ is exactly equal to zero at n + 1 points. This means

that rxðÞ¼0hasn + 1 roots. A polynomial of degree n has exactly n roots (some or

all of which can be complex). Then, rðxÞ must be a polynomial of degree n + 1. This

contradicts our supposition that both pðxÞ and qðxÞ are of degree n. Thus , two

different polynomi als of degree n cannot pass through the same n + 1 points. Only

one polynomial of degree n exists that passes through all n + 1 points.

There are two ways to create an interpolating polynomial function.

(1) Polynomial interpolation Fit a polynomial of degree n to all n + 1 data points.

(2) Piecewise polynomial interpolation Fit polynomials of a lower degree to subsets

of the data.

For example, to ﬁt a polynomial to ten data points, a cubic polynomial

The MATLAB plot function connects adjacent data points using piecewise linear interpolation.

362

Numerical quadrature

can be ﬁtted to three sets of four consecutive points. Three cubic polynomials are

constructed for the three data subsets: x

; x

ðÞ; x

; x

ðÞ,and

; x

ðÞ. Thus, the interpolating domain x

 x  x

is divided into three

subintervals, and interpolating polynomials of degree 3 are constructed for each of

these subintervals.

When the number of data points in the data set is greater than ﬁve, piecewise

polynomial interpolation is preferred over creating a single interpolating polynomial

function that passes through each point. Fitting a polynomial of increasingly higher

degrees to n > 5 data points is strongly discouraged. An interpolating polynomial

will pass through all the points or nodes used to constr uct the polynomial function.

However, in between the nodes, a high-degree polynomial function may exhibit

pronounced oscillatory behavior. In other words, high-de gree polynomial interpo-

lants may produce intermediate values that are far removed from the true path that

connects the data points. This capricious behavior of higher-degree polynomials is

called polynomial wiggle.

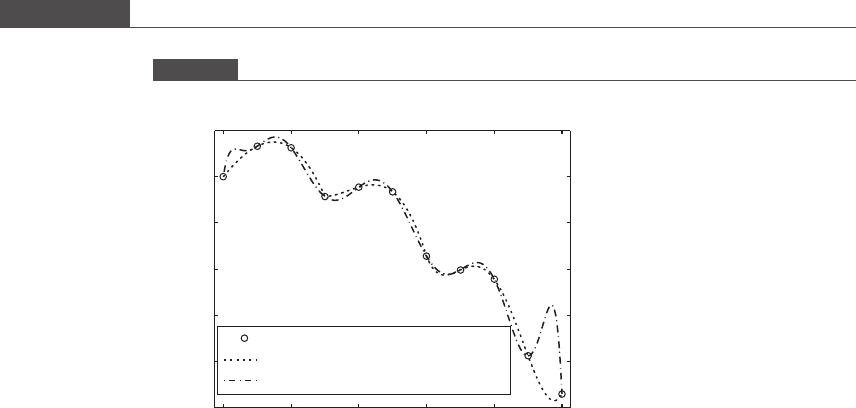
Figure 6.4 shows 11 data points. A tenth-degree polynomial function is con-

structed using all 11 points. A piecewise polynomial function is also constructed in

which the ﬁrst four points (1–4) are ﬁtted with a cubic polynomial, the next set of

four points (4–7) is ﬁtted with a cubic polynomial, while the last set of ﬁve points

(7–11) is ﬁtted with a fourth-degree polynomial. Note that the cubic functions

smoothly connect each point without straying away from the direction (slope) of

the line connecting two adjacent data points. The high degree polynomial function

shows pronounced oscillations between data points. Between the last two data

points, the function shows a large peak that is absent in the data.

If you examine Figure 6.4, you will notice that by choosing non-overlapping

subsets of data points and interpolating with low-order polynomials, slope continu-

ity of the functions may not be guaranteed at the endpoints of each subset. In this

example, discontinuity of the interpolating polynomi al function occurs at the fourth

and seventh data points. A special polynomial interpolating function called a cubic

spline can be used to ensure slope continuity at nodes whi ch join two different

polynomial interpolants. To learn how to construct cubic splines for data interpo-

lation, the reader is referred to Recktenwald (2000). The spline function provided

Figure 6.4

Piecewise polynomial interpolation versus high-degree polynomial interpolation.

0 2 4 6 8 10

−50

−40

−30

−20

−10

f(x)

Nodes

Piecewise polynomial interpolant

10th-degree polynomial interpolant

363

6.2 Polynomial interpolation

by the MATLAB software calculates the piecewise polynomial cubic spline inter-

polant of the user-supplied data.

An interpolating function approximates the function values that lie between the

known data points. The error in approximation depends on (1) the true functional

dependency of the property of interest on the independent variable, (2) the degree of

the interpolating polynomial, and (3) the position of the n + 1 nodes where the

function values are known and used to construct the polynomial interpolant. The

error does not necessarily decrease with increase in the degree of the polynomial used

for interpolation due to the drawbacks of polynomial wiggle.

A straightforward method to determine the coefﬁcients of the nth-degree polyno-

mial is to substitute each data pair x; yðÞinto Equation (6.10). This produces n +1

linear equations. Suppose n = 4, and we have function values at ﬁve points:

; x

,andx

. The set of linear equations can be written in matrix notation:

Ac ¼ y ;

where

A ¼

; c ¼

; y ¼

;

A is called the Vandermonde matrix. This linear problem is not overdetermined, and

we do not need to invoke least-square regression procedures. Solution of the system

of linear equations using methods discussed in Chapter 2 yields the coefﬁcients that

deﬁne the interpolating polynomial. The n + 1 values at which y is speciﬁed must be

unique, otherwise A will be rank deﬁcient and an interpolating polynomial of degree

n cannot be determined.

Using MATLAB

A set of simultaneous linear equations can be solved using the MATLAB backslash

operator (c = A\y). The use of this operator was discussed in Chapter 2. This is one

method to ﬁnd the coefﬁcient matrix c. Another method to determine the constants of

the interpolating polynomial function is to use polyﬁt. The MATLAB polyﬁt

function can be used to calculate the coefﬁcients of a polynomial even when the problem

is not overspeciﬁed. Usage of the polyﬁt function for overdetermined systems was

discussed in Chapter 2. The syntax to solve a fully determinate problem (a set of linear

equations that is consistent and has a unique solution) is the same and is given by

[c, S] = polyﬁt(x, y, n)

where n is the degree of the interpolating polynomial function and is equal to one less

than the number of data points. The output vector c contains the coefﬁcients of the

polynomial of nth degree that passes exactly through the n + 1 points.

A difﬁculty with this method is that the Vandermonde matrix quic kly becomes ill-

conditioned when either the interp olating polynomial degree ≥ 5 or the magnitude of

x is large. As you may remember from Chapter 2, in an ill-conditioned system, the

round-off errors are greatly magniﬁed, producing an inaccurate solution. The con-

dition number of the Vandermonde matrix indicates the conditioning of the linear

364

Numerical quadrature

system. W hen the condition number is high, the solution of the linear system is very

sensitive to round-off errors.

Other methods, such as the Lagrange interpolation formula and Newton’s method of

divided differences, have been developed to calculate the coefﬁcients of the interpola-

ting polynomial. Because of the uniqueness property of an nth-degree polynomial

generated by a set of n + 1 data points, these methods produce the same interpolating

function. However, each method rearranges the polynomial differently, and accord-

ingly the coefﬁcients obtained by each method are different. For the remainder of this

section, we focus on the Lagrange method of interpolation. An important advantage

of this method is that the polynomial coefﬁcients can be obtained without having to

solve a system of linear equations. Lagrange interpolation formulas are popularly

used to derive the Newton–Cotes formulas for numerical integration. For a discussion

on Newton’s method of interpolation, the reader is referred to Recktenwald (2000).

Suppose we wish to linearly interpolate between two data points x

; y

ðÞand

; y

ðÞ. One way to express the linear interpolating function is

pxðÞ¼c

x þ c

We can also write the linear interpolating function as

pðxÞ¼c

x  x

ðÞþc

x  x

ðÞ: (6:11)

When substituting x ¼ x

in Equation (6.11), we obtain

 x

When x ¼ x

, we obtain

 x

Equation (6.11) becomes

pðxÞ¼

x  x

ðÞ

 x

x  x

ðÞ

 x

: (6:12)

Equation (6.12) is the ﬁrst-order Lagrange interpolation formula. We deﬁne the ﬁrst-

order Lagrange polynomials as

ðxÞ¼

x  x

ðÞ

 x

; L

ðxÞ¼

x  x

ðÞ

 x

The interpolating polynomial is simply a linear co mbination of the Lagrange poly-

nomials, i.e.

pxðÞ¼L

þ L

;

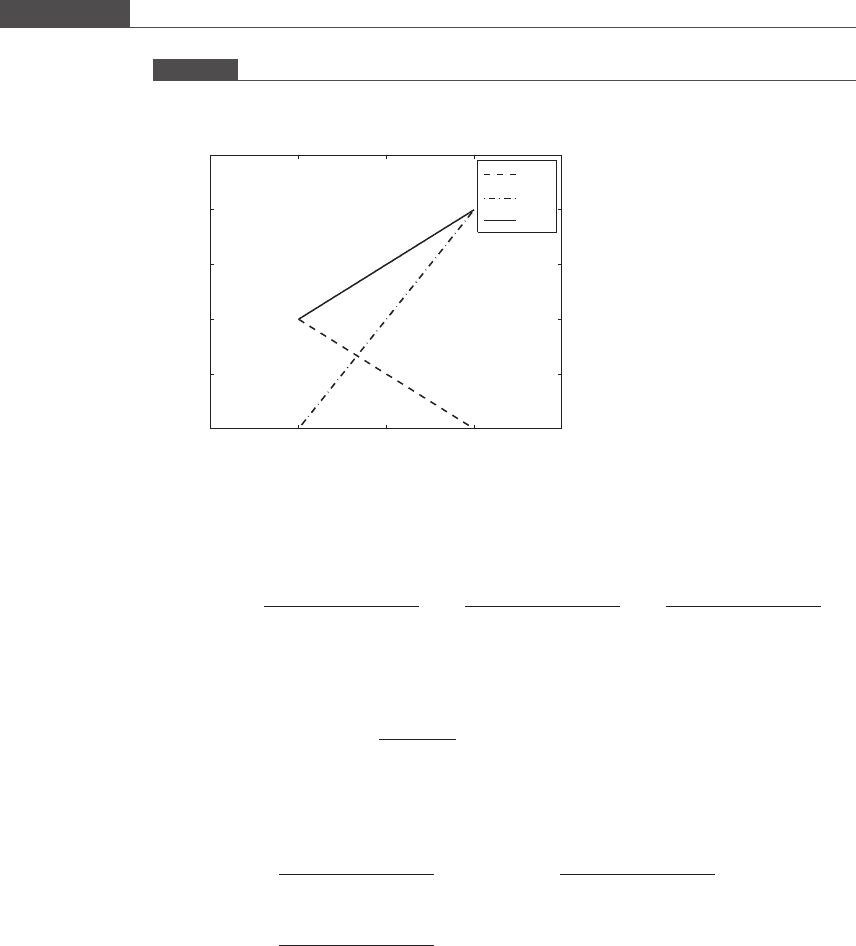
so pðxÞ is equal to the sum of two straight line equations. The ﬁrst term,

xx

ðÞ

x

represents a straight line that passes through two points x

; y

ðÞand x

; 0ðÞ. The

second term,

xx

ðÞ

x

, represents a straight line that passes through the points

; y

ðÞand x

; 0ðÞ. The three straight line equations are plotted in Figure 6.5.

Suppose we wish to interpolate between three points x

; y

ðÞ, x

; y

ðÞ, and x

; y

ðÞ

by constructing a quadratic function. The interpolating function is given by

pxðÞ¼c

x  x

ðÞx  x

ðÞþc

x  x

ðÞx  x

ðÞþc

x  x

ðÞx  x

ðÞ: (6:13)

365

6.2 Polynomial interpolation

The coefﬁcients can be derived in a similar fashion as done for the linear problem.

The second-order Lagrange interpolation formula is given by

pxðÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

;

(6:14)

and can be written compactly as

pxðÞ¼

k¼0

∏

j¼0; j6¼k

x  x



 x



;

where ∏ stands for “the product of.” There are three second-order Lagrange poly-

nomials and each is a quadratic function as follows:

ðxÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

; L

ðxÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

;

ðxÞ¼

x  x

ðÞx  x

ðÞ

 x

ðÞx

 x

ðÞ

Note that L

ðx

Þ is equal to zero when i ¼ 1; 2 and is equal to one when i ¼ 0; L

ðx

is equal to one for i ¼ 1, and is zero when i ¼ 0; i ¼ 2. Similarly, L

ðx

Þ ex actly

equals one when i ¼ 2 and is zero for the other two values of i. Because of this

property of the Lagrange polynomials, we recover the exact value y

of the function

when the corresponding x

value is plugged into the interpolation formula. Each

term L

represents a quadratic polynomial. The interpolating polynomial pðxÞ is

obtained by summing the three quadratic Lagrange polynomials. Figure 6.6 dem-

onstrates how the sum of three quadratic functions produces a second-degree

interpolating polynomial.

An advantage of the Lagrange method is that round-off errors are less likely to

creep into the calculation of the Lagrange polynomials.

Figure 6.5

The interpolating polynomial pðxÞ passes through two points (1, 1) and (2, 2). The sum of the two dashed lines

produces the interpolating polynomial.

0.5 1 1.5 2 2.5

0.5

1.5

2.5

p(x)

366

Numerical quadrature