King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

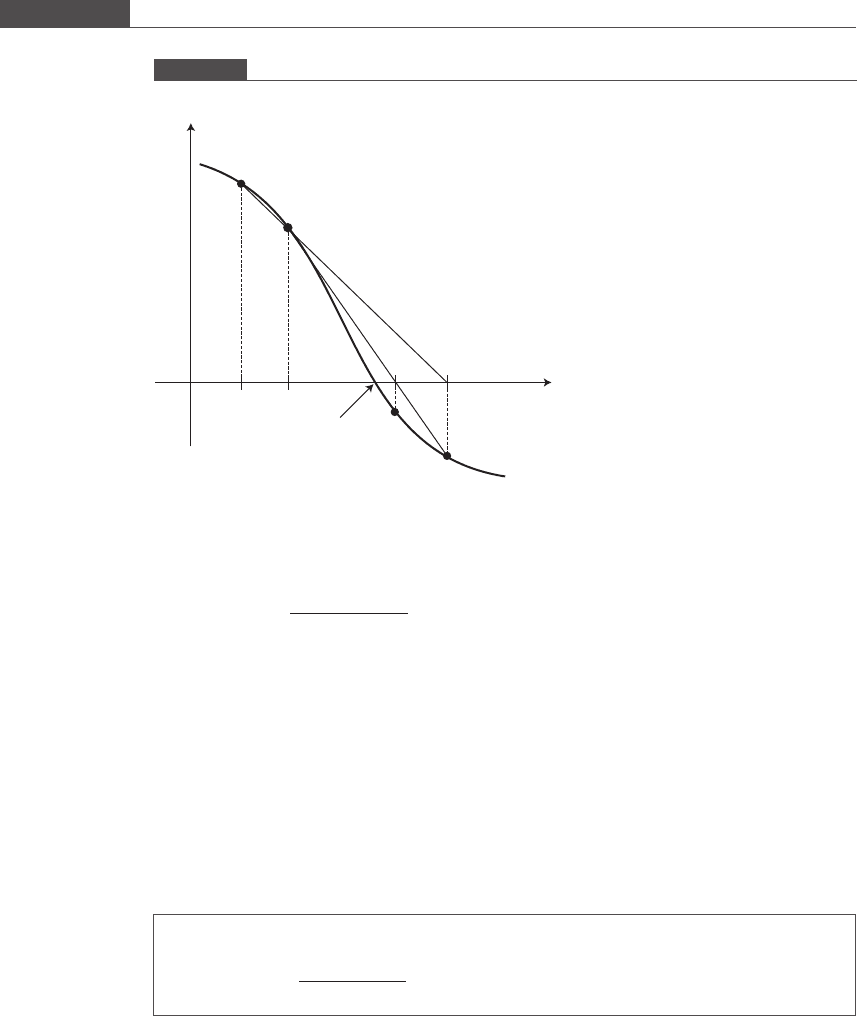
used to calculate the new estimate x

of the root based on the secant line connecting

points x

and x

¼ x



ðÞðx

 x

ðÞfðx

: (5:12)

The derivation of Equation (5.12) is described in Section 5.3. Substituting Equation

(5.33) into Equation (5.19) also produces Equation (5.12). This procedure of root

estimation is very similar to the regula-falsi method with the exception that the two

initial estimates are not required to bracket the root. Therefore, the ﬁrst two initial

guesses x

and x

may be ch osen such that they both lie on the same side of the x-axis

with respect to the location of the root. Figure 5.13 illustrates graphically the

algorithm prescribed by this method.

The next estimate x

of the root is obtained from the inter section of the secant line

joining points (x

, f(x

)) and (x

, f( x

)) with the x-axis. Equation (5.12) can be

generalized as follows:

Secant method

iþ1

¼ x



fðx

Þðx

 x

i1

fðx

Þfðx

i1

: (5:34)

Note that in this procedure an interval bracketing the root is not sought. At any

iteration, the actual root may lie outside the interval contained by the two previous

estimates that generate the secant line. Since the algorithm does not force successive

approximations of the root to lie within a shrinking interval that en capsulates the

root, divergence of the solution technique is possible for situations in which the

calculated slope of the secant line approaches or is near 0.

A note of caution: if the function has either a large (steep) slope or a very

shallow slope near the root, or if the points x

and x

i1

are very close together,

subtractive cancellation in the terms ðx

 x

i1

Þ and/or fx

ðÞfðx

i1

Þ can result in

Figure 5.13

Illustration of the secant method.

f(x)

Actual root

337

5.6 Secant method

large round-off error due to loss of signiﬁcance (see Chapter 1 for a discussion of

round-off error). It is highly recommended that you monitor the values of x and f (x)

generated in the successive iterations to catch any inadvertent difﬁculties that may

arise during convergence to the root. In such cases, you can choose an alternate

method or a modiﬁcation to the existing method to contain the errors. For example,

if x

and x

i1

tend to approach each other too closely, one may ﬁx x

i1

and allow x

change to prevent signiﬁcant round-off errors from corrupting the estimates.

The secant method uses the following algorithm to ﬁnd a zero of f (x).

(1) Determine two initial estimates x

and x

of the root of the function f (x), which are

not required to bracket the root.

(2) Calculate the next estimate of the root using the equation x

iþ1

¼ x



ðÞðx

 x

i1

ðÞfðx

i1

(3) Repeat step 2 until the method has converged upon a solution.

The convergence rate for the secant method is given by Equation (5.35), and is

superlinear for simple roots:

iþ1



ðx



ðx





0:618

jEj

1:618

: (5:35)

Here, the order of convergence r ¼



1 þ

ﬃﬃﬃ



=2 ¼ 1:618 is the golden ratio, and

C ¼

ðx



ðx





0:618

The order of convergence is linear for functions that have multiple roots.

5.7 Solving systems of nonlinear equations

Many engineering problems involve a system of nonlinear equations in two or more

independent varia bles that must be solved simultaneously to yield a solution.

Solving nonlinear systems of equations is more challenging than solving a single

nonlinear equation or a system of linear equations. Iterative techniques can be

employed for ﬁnding a solution to systems of nonlinear equations. As with all

numerical root- ﬁnding techniques for nonlinear equations, the number of iterations

to be carried out is not known a priori, convergence cannot be guaranteed unless

certain pre-speciﬁed conditions are met, and multiple solutions may exist although

the solution technique may not reveal all of them.

Newton’s method, which was introduced in Section 5.5 to solve a single nonlinear

equation, can be generalized to handle a system of two or more nonlinear equations.

A system of n nonlinear equations in n independent varia bles can be written as

follows:

ðx

; x

; ...; x

Þ¼0;

ðx

; x

; ...; x

Þ¼0;

ðx

; x

; ...; x

Þ¼0:

If x ¼½x

; x

; ...; x

, then this system of equations can be repres ented as follows:

338

Root-finding techniques for nonlinear equations

FxðÞ¼

; x

; ...; x

ðÞ

; x

; ...; x

ðÞ

; x

; ...; x

ðÞ

: (5:36)

Box 5.2B Equilibrium binding of multivalent ligand in solution to cell surfaces

This problem is re-solved using the secant method. A function in MATLAB was written called

secantmethod that implements the algorithm described above to solve for the root of a nonlinear

equation. To solve Equation (5.27), secantmethod calls the user-defined function

ReceptorLigandEqbmBinding and begins the search for the root using two initial guesses

= 8000 and x

= 10 400 receptors:

secantmethod(‘ReceptorLigandEqbmBinding’, 8000, 10400, 0.5, 0.5)

i x(i-1) x(i) x(i+1) f(x(i-1)) f(x(i))

1 8000.0000 10400.0000 10472.6067 -2609.378449 -76.622878

2 10400.0000 10472.6067 10470.7834 -76.622878 1.973693

3 10472.6067 10470.7834 10470.7850 1.973693 -0.001783

MATLAB program 5.9

function secantmethod(func, x0, x1, tolx, tolfx)

% Secant method used to solve a nonlinear equation in x

% Input variables

% func : nonlinear function

%x0:ﬁrst initial guess value

% x1 : second initial guess value

% tolx : tolerance for error in estimating root

% tolfx: tolerance for error in function value at solution

% Other variables

maxloops = 50;

fx0 = feval(func,x0);

fx1 = feval(func,x1);

fprintf(‘ i x(i-1) x(i) x(i+1) f(x(i-1)) f(x(i)) \n’);

% Iterative solution scheme

for i = 1:maxloops

x2 = x1 - fx1*(x1 - x0)/(fx1 - fx0);

fx2 = feval(func,x2);

fprintf(‘%2d %5.4f %5.4f %5.4f %7.6f %7.6f \n’, ...

i,x0,x1,x2, fx0,fx1);

if (abs(x2 - x1) <=tolx && abs(fx2) < tolfx)

break % Jump out of the for loop

end

x0 = x1;

x1 = x2;

fx0 = fx1;

fx1 = fx2;

end

339

5.7 Solving systems of nonlinear equations

Let x

ðkÞ

¼½x

kðÞ

; x

kðÞ

; ...; x

kðÞ

 be the kth estimate for the root. The initial guess,

which lies near the root, is x

ð0Þ

¼ x

0ðÞ

; x

0ðÞ

; ...; x

0ðÞ

: Each function f can be

expanded using the Taylor series about x

ð0Þ

.Ifx

ð0Þ

is located close to the root, then

the higher-order terms of Δx

ð0Þ

are much smaller than the zero- and ﬁrst- order terms

in the expansion and can be neglected as is done here:

0ðÞ

þ Δx

0ðÞ

; ...; x

0ðÞ

þ Δx

0ðÞ



’ f

0ðÞ

; ...; x

0ðÞ



þ Δx

0ðÞ

∂f

∂x



0ðÞ

;...;x

0ðÞ

þΔx

0ðÞ

∂f

∂x



0ðÞ

;...;x

0ðÞ

þ...

þ Δx

0ðÞ

∂f

∂x



0ðÞ

;...;x

0ðÞ

þ Δx

0ðÞ

; ...; x

0ðÞ

þ Δx

0ðÞ



’ f

0ðÞ

; ...; x

0ðÞ



þ Δx

0ðÞ

∂f

∂x



0ðÞ

;...;x

0ðÞ

þΔx

0ðÞ

∂f

∂x



0ðÞ

;...;x

0ðÞ

þ...

þ Δx

0ðÞ

∂f

∂x



0ðÞ

;...;x

0ðÞ

We seek a solution x þ Δx to the system of equations such that F(x þ Δx)=0.

Therefore, if we set

0ðÞ

þ Δx

0ðÞ

; ...; x

0ðÞ

þ Δx

0ðÞ



¼ 0

0ðÞ

þ Δx

0ðÞ

; ...; x

0ðÞ

þ Δx

0ðÞ



¼ 0;

we obtain the matrix equation

0ðÞ



Δx

0ðÞ

¼Fx

0ðÞ



: (5:37)

Here,

JxðÞ¼

∂f

∂x

∂f

∂x

...

∂f

∂x

∂f

∂x

∂f

∂x

...

∂f

∂x

is called the Jacobian of F.

Equation (5.37) can be generalized as follows for any iteration k:

kðÞ



Δx

kðÞ

¼Fx

kðÞ



; (5:38)

340

Root-finding techniques for nonlinear equations

where

kþ1ðÞ

¼ x

kðÞ

þ Δx

kðÞ

: (5:39)

Equations (5.38) and (5.39) highlight the tw o-step solution technique of Newton’s

method. Equation (5.38) forms a set of linear equations which are solved for Δx

kðÞ

Once Δx

kðÞ

is obtained, the next approximation of the root x

kþ1ðÞ

is easily derived

using Equation (5.39).

Convergence of Equations (5.38) and (5.39) will occur only if certain conditions

similar to those discussed in Section 5.5 are met.

(1) All functions and their partial derivatives are continuous at and near the root.

(2) The Jacobian is non-singular, i.e. the determinant JxðÞ

6¼ 0. (Refer to Section 2.2

for a discussion on singular matrices and calculati on of the determinant.)

(3) The initial guess value is located close enough to the root.

The algorithm is summarized as follows.

(1) Provide an initial estimate x

ð0Þ

of the root of the multi-equation system F(x).

(2) Determine the analytical form of the Jacobian JxðÞ.

(3) Calculate F(x) and JxðÞat x

ðkÞ

(4) Solve the equation Jx

kðÞ



Δx

kðÞ

¼Fx

kðÞ



for Δx

kðÞ

(5) Calculate the new approximation of the root x

kþ1ðÞ

¼ x

kðÞ

þ Δx

kðÞ

(6) Set x

kðÞ

¼ x

kþ1ðÞ

(7) Repeat (3)–(6) until the method has converged upon a solution.

Example 5.3

Let’s consider an example problem in which we have two nonlinear equations in two variables:

¼ 3x

þ x

 10 ¼ 0;

¼ x

þ x

 1 ¼ 0:

This system of equations has two solutions (−1.5942, −1.5414) and (1.5942, −1.5414).

Note that this

set of equations can easily be solved by hand to obtain the exact solution.

The Jacobian for this system of equations is

J ¼

∂f

∂x

∂f

∂x

∂f

∂x

∂f

∂x



Let our initial guess x

(0)

be (1, − 1), so

0ðÞ



6 2



and Fx

0ðÞ



6

1



We solve the set of equations

6 2



Δx



¼

6

1



and obtain

MATLAB graphics: One way of studying the behavior of functions in two variables involves drawing

contour plots using the MATLAB contour function. The intersection of the contour lines for both

functions at f = 0 provides information on the location of the root. Use of contour is illustrated in

Chapter 8.

341

5.7 Solving systems of nonlinear equations

Δx

ð0Þ

¼ 0:8; Δx

ð0Þ

¼0:6:

Therefore,

ð1Þ

¼ x

ð0Þ

þ Δx

ð0Þ

¼ 1:8;

ð1Þ

¼ x

ð0Þ

þ Δx

ð0Þ

¼1:6:

With x

(1)

= (1.8, −1.6), we evaluate

1ðÞ



10:8 3:2

3:61



and Fx

1ðÞ



2:28

0:64



We solve the set of equations

10:8 3:2

3:61



Δx



¼

2:28

0:64



to obtain

Δx

ð1Þ

¼0:1939; Δx

ð1Þ

¼ 0:0581:

Therefore,

ð2Þ

¼ x

ð1Þ

þ Δx

ð1Þ

¼ 1:6061;

ð2Þ

¼ x

ð1Þ

þ Δx

ð1Þ

¼1:5419:

Evidently, convergence of the solution to the one of the two roots is imminent.

On the other hand, if we were to try to solve a similar set of equations,

¼ x

þ x

 4 ¼ 0;

¼ x

þ x

þ 2 ¼ 0;

the solution does not converge. As an exercise, verify that the Jacobian becomes singular at the root (0, −2).

A difﬁculty encountered with Newton’s method is that convergence of the equations is

contingent on the availability of good initial guesses, and this can be difﬁcult to obtain

for a system of multiple nonlinear equations. An algorithm is likely to converge if

(1) the algorithm moves closer to the solution with every iteration, i.e. Fx

kþ1ðÞ





kðÞ





,and

(2) the correction to the estimate of the root does not become increasingly large, i.e.

kþ1ðÞ

 x

ðkÞ



δ, where δ is some upper limiting value.

An alternate approach to using linear methods to determine Δx

kðÞ

is to solve a

nonlinear optimization problem in which we seek Δx

kðÞ

values that minimize



kðÞ



Δx

kðÞ

þ Fx

kðÞ





subject to Δx

kðÞ

δ. This method can be used even if J becomes singular. The

algorithm proceeds as follows.

(1) Determine Δx

kðÞ

using a nonlinear optimization technique to minimize

kðÞ



Δx

kðÞ

þ Fx

kðÞ





(2) If Fx

kþ1ðÞ





kðÞ





, then reduce δ a nd return to step 1.

(3) If Fx

kþ1ðÞ



 0, then terminate algorithm or else return to step 1 to start the next

iteration.

342

Root-finding techniques for nonlinear equations

Box 5.4 The Fahraeus–Lindquist effect

A well-known phenomenon that results from the tendency of RBCs to concentrate in the core

region of a blood vessel is the decrease in apparent blood viscosity as blood vessel diameter is

reduced. This phenomenon is called the Fahraeus–Lindquist effect and occurs due to the

changing proportion of the width of the cell-free plasma layer with respect to the core RBC

region. As the vessel diameter decreases, the thickness of the cell-free plasma layer δ (viscosity

μ = 1.2 cP) increases. Since the viscosity of this outer RBC-depleted layer is much lower than

that of the RBC-rich core region, the overall tube viscosity exhibits a dependence on the vessel

diameter. If μ

is the viscosity of blood in a feed vessel (upstream vessel) of large diameter (e.g.

of an artery in which δ ~ 0 (Fournier, 2007)), then the viscosity ratio (μ

apparent

/μ

) < 1.0, where

apparent

is the apparent viscosity in a blood vessel of smaller size. Equation (5.40) relates this

viscosity ratio to the hematocrit (volume fraction of RBCs in blood) in the feed vessel and the core

region of the vessel of interest:

apparent

1  α

1  σ

core

; (5:40)

where

core

is the core region hematocrit,

is the feed vessel hematocrit,

σ ¼ 1  δ=R,

δ = thickness of the plasma layer,

R = radius of blood vessel,

α ¼ 0:070 exp 2:49H þ

1107

expð1:69HÞ



, and

T is the temperature (K).

If H

(hematocrit of feed or large blood vessel) = 0.44, R =15μm, and T = 310 K are the values

provided to you, and experimental data (Gaehtgens, 1980; Gaehtgens et al., 1980) also provide

apparent

=μ

¼ 0:69, use Equation (5.40) in conjunction with Equation (5.3), repeated here

core

¼ H

1 þ

ð1  σ

21 σ

ðÞþσ

ð1  α

core

Þ½

; (5:3)

to determine the core region hematocrit H

core

and the thickness of the plasma layer δ for this particular

blood vessel diameter (Fournier, 2007).

We have two nonlinear equations in two independent variables: H

core

and σ. First, Equations (5.3) and

(5.40) must be rewritten in the form f (H

core

, σ) = 0; i.e.

core

; σðÞ¼1 þ

ð1  σ

21 σ

ðÞþσ

ð1  α

core

Þ½



core

¼ 0(5:41)

and

core

; σðÞ¼

1  α

1  σ

core



apparent

¼ 0: (5:42)

Our next task is to determine the Jacobian for this problem. We have

∂f

∂H

core

1  σ



core

21 σ

ðÞþσ

1  α

core

ðÞ½

 1 þ H

core

2:49 

1870:83

1:69H

core





;

343

5.7 Solving systems of nonlinear equations

∂f

∂σ

4 σ

 1



σ 21 σ

ðÞþσ

1  α

core

ðÞ½



41 σ



1  σ

1  α

core

ðÞ



21 σ

ðÞþσ

1  α

core

ðÞ½

;

∂f

∂H

core

ð1  α

Þα

core

1  σ

core

½

 1 þ H

core

2:49 

1870:83

1:69H

core



;

∂f

∂σ

4σ

ð1  α

Þα

core

½1  σ

core



In this problem the Jacobian is defined as follows:

J ¼

∂f

∂H

core

∂f

∂σ

∂f

∂H

core

∂f

∂σ

: (5:43)

A MATLAB function program FahraeusLindquistExample.m was created to calculate the values of f

and

(Equations (5.41) and (5.42)) as well as the Jacobian 2 × 2 matrix defined in Equation (5.43) for the

supplied values of H

core

and σ. Another MATLAB function program called gen_newtonmethod2.m was

constructed to use the generalized Newton’s method (Equations (5.38) and (5.39)) to solve a system of

two nonlinear equations in two variables.

Using MATLAB

(1) At every iteration, we solve the linear system of equations Jx

kðÞ



Δx

kðÞ

¼Fx

kðÞ



to determine

Δx

kðÞ

. This is equivalent to solving the linear system of equations Ax = b. MATLAB includes built-

in techniques to solve a system of linear equations Ax = b. The syntax: x = A\b (which uses the

backslash operator) tells MATLAB to find the solution to the linear problem Ax = b, which reads as

b divide by A. Note that MATLAB does not compute the inverse of A to solve a system of

simultaneous linear equations (see Chapter 2 for further details).

(2) Because we use MATLAB to solve a system of simultaneous linear equations, x and b must be

specified as column vectors. Note that b should have the same number of rows as A in order to

perform the operation defined as x = A\b.

(3) Here, when using the specified tolerance values to check if the numerical algorithm has reached

convergence, we enforce that the solution for all independent variables and the resulting function

values meet the tolerance criteria. The relational operator ≤ checks whether all dx values and fx

values are less than or equal to the user-defined tolerance specifications. Because we are using

vectors rather than scalar values as operands, we must use the element-wise logical operator &,

instead of the short-circuit operator && (see MATLAB help for more information). When using the &

operator, the if statement will pass control to the logical expression contained in the if - end

statement only if all of the elements in the if statement argument are non-zero (i.e. true).

MATLAB program 5.10

function [f, J] = Fahraeus LindquistExample(x)

% Calculation of f1 and f2 and Jacobian matrix for Box 5.4

% Input Variables

hcore = x(1); % Core region hematocrit

sigma = x(2); % 1 - delta/R

344

Root-finding techniques for nonlinear equations

% Output Variables

f= zeros(2,1); %functioncolumn vector[f1;f2](should notbea row vect or)

J = zeros(2,2); % Jacobian 2x2 matrix

% Constants

hfeed = 0.44; % hematocrit of the feed vessel or large artery

temp = 310; % kelvin : temperature of system

viscratio = 0.69; % ratio of apparent viscosity in small vessel

% to that of feed vessel

% Calculating variables

sigma2 = sigma^2;

sigma3 = sigma^3;

sigma4 = sigma^4;

alphafeed = 0.070*exp(2.49*hfeed + (1107/temp)*exp(-1.69*hfeed));

alphacore = 0.070*exp(2.49*hcore + (1107/temp)*exp(-1.69*hcore));

f1denominator = 2*(1-sigma2)+sigma2*(1-alphacore*hcore);

f2denominator = 1 - sigma4*alphacore*hcore;

% Evaluating the function f1 and f2

% Equation 5.41

f(1) = 1+ ((1-sigma2)^2)/sigma2/f1denominator - hcore/hfeed;

% Equation 5.42

f(2) = (1 - alphafeed*hfeed)/f2denominator - viscratio;

% Evaluating the Jacobian Matrix

% J(1,1) = df1/dhcore

J(1,1) = ((1-sigma2)^2)*alphacore;

J(1,1) = J(1,1)/(f1denominator^2);

J(1,1) = J(1,1)* ...

(1 + hcore*(2.49 - 1870.83/temp*exp(-1.69*hcore))) - 1/hfeed;

% J(1,2) = df1/dsigma

J(1,2) = 4*(sigma2 - 1)/sigma/f1denominator;

J(1,2) = J(1,2)-4*(1-sigma2)^2*(1-sigma2*(1-alphacore*hcore))/. . .

sigma3/f1denominator^2;

% J(2,1) = df2/dhcore

J(2,1) = sigma4*(1-alphafeed*hfeed)*alphacore/f2denominator^2;

J(2,1) = J(2,1)*(1 + hcore*(2.49 - 1870.83/temp*exp(-1.69*hcore)));

% J(2,2) = df2/dsigma

J(2,2) = 4*sigma3*(1-alphafeed*hfeed)*alphacore*hcore;

J(2,2) = J(2,2)/f2denominator^2;

MATLAB program 5.11

function gen_newtonsmethod2(func, x, tolx, tolfx)

% Generalized Newton’s method to solve a system of two nonlinear

% equations in two variables

345

5.8 MATLAB function fzero

Thus far, we solved nonlinear equations using only one technique at a time.

However, if we solve for a root of a nonlinear equation by combining two or more

techniques, we can, for example, achieve the coupling of the robustness of a brack-

eting method of root ﬁnding with the convergence speed of an open-interval method.

Such combinations of methods of root ﬁnding are termed hybrid methods and are

much more powerful than using any single method alone. The MATLAB function

fzero is an example of using a hybrid method to ﬁnd roots of a nonlinear equation.

The fzero function combines the reliable bisection method with faster convergence

methods: the secant method and inverse quadratic interpolation. The inverse

quadratic interpolation method is similar to the secant method, but instead of

using two endpoints to produce a secant line as an approximation of the function

near the root, three data points are used to approximate the function as a quadratic

% Input variables

% func : function that evaluates the system of nonlinear equations and

% the Jacobian matrix

% x : initial guess values of the independent variables

% tolx : tolerance for error in the solution

% tolfx : tolerance for error in function value

% Other variables

maxloops = 20;

[fx, J] = feval(func,x);

fprintf(‘ i x1(i+1) x2(i+1) f1(x(i)) f2(x(i)) \n’);

% Iterative solution scheme

for i = 1:maxloops

dx = J \ (-fx);

x=x+dx;

[fx, J] = feval(func,x);

fprintf(‘%2d %7.6f %7.6f %7.6f %7.6f \n’,...

i, x(1), x(2), fx(1), fx(2));

if (abs(dx) <=tolx & abs(fx) < tolfx)

% not use of element-wise AND operator

break % Jump out of the for loop

end

We run the user-defined function gen_newtonsmethod2 and specify the appropriate arguments

to solve our nonlinear problem in two variables. We use starting guesses of H

core

= 0.44 and δ =3

μmorσ = 0.8:

gen_newtonsmethod2(‘FahraeusLindquistExample ’,[0.44; 0.8],

0.002, 0.002)

i x1(i+1) x2(i+1) f1(x(i)) f2(x(i))

1 0.446066 0.876631 0.069204 0.020425

2 0.504801 0.837611 -0.006155 0.000113

3 0.500263 0.839328 0.001047 -0.000001

4 0.501049 0.839016 -0.000181 -0.000000

The solution obtained is H

core

= 0.501 and σ = 0.839 or δ = 2.41 μm.

346

Root-finding techniques for nonlinear equations