King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

A MATLAB program is written using the bisection algorithm to solve Equation (5.11). First a function

called hematocrit is created in a separate function m-file called hematocrit.m to evaluate f(x)

(Equation (5.11)). Another function is created in MATLAB called bisectionmethod which

performs the algorithm of the bisection method. The MATLAB function feval is used in

bisectionmethod to evaluate the hematocrit function at the specified value of x.As

part of the algorithm, it is necessary to define the maximum number of iterations that the program will

allow to prevent indefinite looping in situations where convergence is elusive. The program code is

listed in the following. Note that the plotting commands have not been included in order to keep the

code simple and straightforward. Appendix A discusses the MATLAB plot function.

MATLAB program 5.1

function f = hematocrit(x)

% Constants

delta = 2.92; % microns : plasma layer thickness

R = 15; % microns : radius of blood vessel

hinlet = 0.44; % hematocrit

temp = 310; % Kelvin : temperature of system

% Calculating variables

sigma = 1 - delta/R;

sigma2 = sigma^2;

alpha = 0.070.*exp(2.49.*x + (1107/temp).*exp(-1.69.* x));

% Equation 5.3

numerator = (1-sigma2)^2;

denominator = sigma2*(2*(1-sigma2)+sigma2*(1-alpha.*x));

% Equation 5.11

f = 1+numerator./denominator -x./hinlet;

MATLAB program 5.2

function bisectionmethod(func,ab, tolx, tolfx)

% Bisection algorithm used to solve a nonlinear equation in x

% Input variables

% func : nonlinear function

% ab : bracketing interval [a, b]

% tolx : tolerance for error in estimating root

% tolfx : tolerance for error in function value at solution

% Other variables

maxloops = 50; % maximum number of iterations allowed

% Root-containing interval [a b]

a = ab(1);

b = ab(2);

fa = feval(func, a); % feval evaluates func at point a

fb = feval(func, b); % feval evaluates func at point b

% Min number of iterations required to meet criterion of Tolx

minloops = ceil(log(abs(b-a)/tolx)/log(2));

% ceil rounds towards +Inf

fprintf(‘Min iterations for reaching convergence = %2d \n’,minloops)

317

5.2 Bisection method

fprintf(‘ i x f(x) \n’); % \n is carriage return

% Iterative solution scheme

for i = 1:maxloops

x = (a+b)/2; % mid-point of interval

fx = feval(func,x);

fprintf(‘%3d %5.4f %5.4f \n’,i,x,fx);

if (i>= minloops && abs(fx) < tolfx)

break % Jump out of the for loop

end

if (fx*fa < 0) % [a x] contains root

fb = fx; b = x;

else % [x b] contains root

fa = fx; a = x;

end

We specify the maximum tolerance to be 0.002 for both the root and the function value at the estimated

root. In the Command Window, we call the function bisectionmethod and include the

appropriate input variables as follows:

bisectionmethod(‘hematocrit’,[0.5 0.55],0.002,0.002)

Min iterations for reaching convergence = 5

i x f(x)

1 0.5250 0.0035

2 0.5375 −0.0230

3 0.5313 −0.0097

4 0.5281 −0.0031

5 0.5266 0.0002

Figure 5.5 graphically shows the location of the midpoints calculated at every iteration.

Note from the program output that the first approximation of the root is rather good and the next two

approximations are actually worse off than the first one. Such inefficient convergence is typically

observed with the bisection method.

Figure 5.5.

Graphical illustration of the iterative solution of the bisection method.

0.5 0.51 0.52 0.53 0.54 0.55

−0.06

−0.04

−0.02

0.02

0.04

0.06

f(x)

318

Root-finding techniques for nonlinear equations

5.3 Regula-falsi method

This numerical root-ﬁnding technique is also known as “the method of false

position” or the “method of linear interpolation,” and is much like the bisection

method, in that a root is always sought within a bracketing interval. The name

“regula-falsi” derives from the fact that this iterative method produces an estimate

of the root that is “false,” or only an ap proximation, yet as each iteration is carried

out according to the “rule,” the method converges to the root. The methodology

for determining the root closely follows the steps enumerated in Section 5.2 for the

bisection algorithm. An interval [x

, x

], where x

and x

are two initial guesses

that contain the root, is chosen in the same fashion as discussed in Section 5.2.

Note that the function f(x) whose root is being sought must be continuous within

the chosen interval (see Section 5.2). In the bisection method, an interval is

bisected at every iteration so as to halve the bounded error. However, in the

regula-falsi method, a line called a secant line is drawn connecting the two interval

endpoints that lie on either side of the x-axis. The secant line intersects the x-axis

at a point x

that is closer to the true root than either of the two interval endpoints

(see Figure 5.6). The point x

divides the initial interval into two subintervals [x

]and[x

, x

], only one of which contains the root. If f (x

)·f(x

) < 0 then the

points x

and x

on f(x) necessarily straddle the root. Otherwise the root is

contained in the interval [x

, x

We can write an equation for the secant line by equati ng the slopes of

(1) the line joining points (x

, f(x

)) and (x

, f(x

)) and

(2) the line joining points (x

, f(x

)) and (x

, 0).

Thus,

ðÞfðx

 x

0  fðx

 x

Figure 5.6

Illustration of the regula-falsi method.

f(x

)

f(x

)

f(x

)

f(x

)

Actual root

f(x)

3rd interval [x

]

2nd interval [x

]

1st interval [x

]

319

5.3 Regula-falsi method

Regula-falsi method:

¼ x



fðx

Þðx

 x

fðx

Þfðx

: (5:12)

The algorithm for the regula-falsi root-ﬁnding process is as follows.

(1) Select an interval [x

, x

] that brackets the root, i.e. f(x

)·f(x

)<0.

(2) Calculate the next estimate x

of the root within the interval using Equation (5.12).

This estimate is the point of intersection of the secant line joining the endpoints of

the interval with the x-axis. Now, unless x

is precisely the root, i.e. unless f(x

)=0,

the root must lie either in the interval [x

, x

]orin[x

, x

(3) To determine which interval contains the root, f(x

) is calculated and then compared

with f(x

) and f(x

(a) If f(x

)·f(x

) < 0, then the root is located in the interval [x

, x

], and x

replaced with the value of x

, i.e. x

= x

(b) If f(x

)·f(x

) > 0, the root lies within [ x

, x

], and x

is set equal to x

(4) Steps (2)–(3) are repeated until the algorithm ha s converged upon a solution. The

criteria for attaining convergence may be either or both

(a) x

new

 x

old

TolðxÞ;

(b) jf ðx

new

Þj

TolðfðxÞÞ.

This method usually converges to a solution faster than the bisection method.

However, in situations where the function has signiﬁcant curvature with conca vity

near the root, one of the endpoints stays ﬁxed throughout the numerical procedure,

while the other endpoint inches towards the ro ot. The shifting of only one endpoint

while the other remains stagnant slows convergence and many iterations may be

required to reach a solution within toler able error. However, the solution is guar-

anteed to converge as subsequent root estimates move closer and closer to the actual

root.

5.4 Fixed-point iteration

The ﬁxed-point iterative method of root-ﬁnding involves the least amount of calcu-

lation steps and variable overhead per iteration in comparison to other methods, and

is hence the easiest to program. It is an open interval method and requires only one

initial guess value in proximity of the root to begin the iterative pro cess. If f(x) is the

function whose zeros we seek, then this method can be applied to solve for one or

more roots of the function, if f (x) is continuous in proximity of the root(s). We

express f(x)asf(x)=g(x)–x, where g(x) is another function of x that is continuous

within the interval between the root x* and the initial guess value of the root supplied

to the iterative procedure. The equ ation we wish to solve is fxðÞ¼0; and this is

equivalent to

x ¼ gxðÞ: (5:13)

That value of x for which Equation (5.13) holds is a root x*offðxÞ and is called a

ﬁxed point of the function gxðÞ: In geometric terms, a ﬁxed point is located at the

point of intersection of the curve y ¼ gxðÞwith the straight line y = x.

To begin the iterative method for locating a ﬁxed point of g (x), simply substitute

the initial root estimate x

into the right-hand side of Equation (5.13). Evaluating

320

Root-finding techniques for nonlinear equations

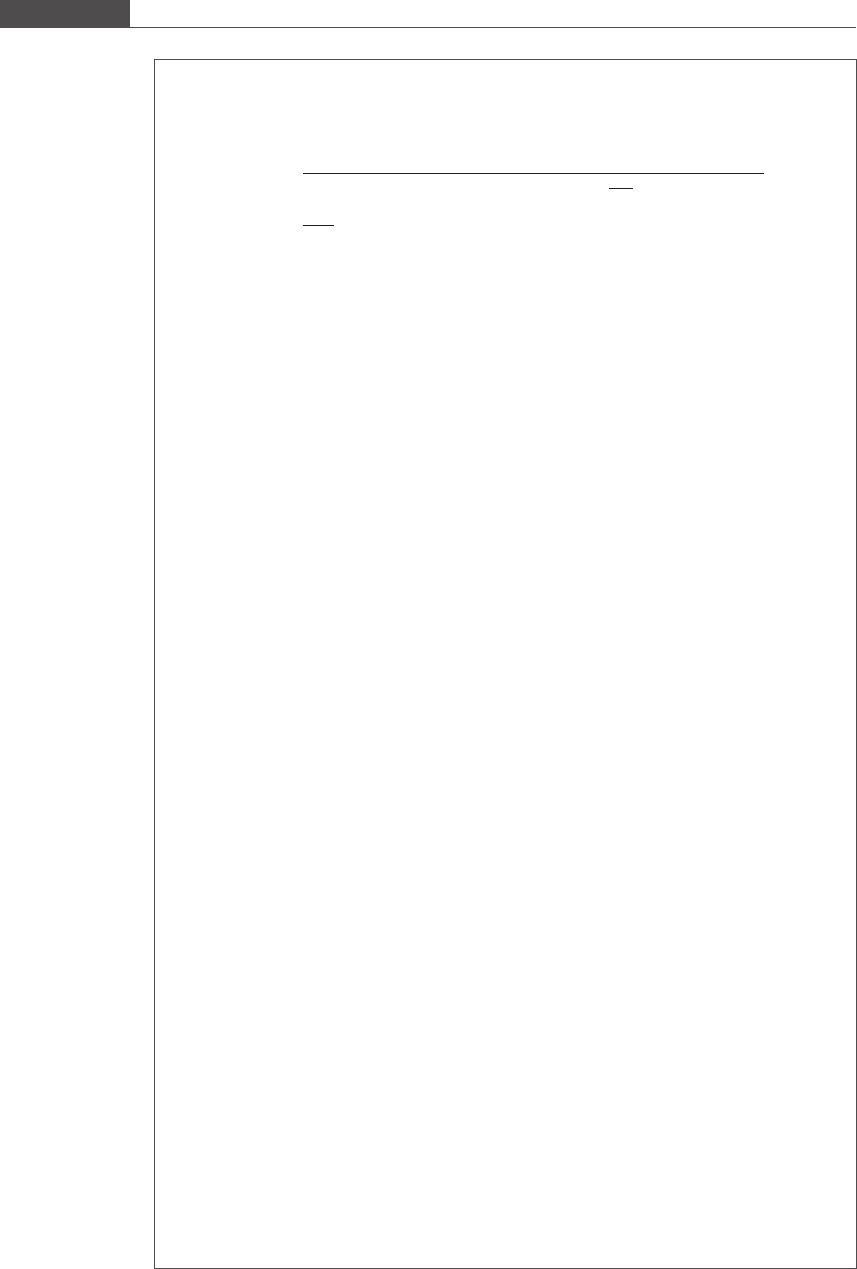
Box 5.1C Rheological properties of blood

We re-solve Equation (5.11) using the regula-falsi method with an initial bracketing interval of [0.5 0.55]:

ðÞ

¼ 1 þ

ð1  σ

21 σ

ðÞþσ

ð1  0:070 exp 2:49x þ

1107

expð1:69xÞ



xÞ





0:44

(5:11)

From Figure 5.3 it is evident that the curvature of the function is minimal near the root and therefore we

should expect quick and efficient convergence.

A MATLAB function regulafalsimethod is written, which uses the regula-falsi method for

root-finding to solve Equation (5.11):

regulafalsimethod(‘hematocrit’,[0.5 0.55],0.002, 0.002)

i x f(x)

1 0.526741 −0.000173

2 0.526660 −0.000001

The regula-falsi method converges upon a solution in the second iteration itself. For functions of

minimal (inward or outward) concavity at the root, this root-finding method is very efficient.

MATLAB program 5.3

function regulafalsimethod(func, x0x1, tolx, tolfx)

% Regula-Falsi method used to solve a nonlinear equation in x

% Input variables

% func : nonlinear function

% x0x1 : bracketing interval [x0, x1]

% tolx : tolerance for error in estimating root

% tolfx: tolerance for error in function value at solution

% Other variables

maxloops = 50;

% Root-containing interval [x0, x1]

x0 = x0x1(1); x1 = x0x1(2);

fx0 = feval(func, x0); fx1 = feval(func, x1);

fprintf(‘ i x f(x) \n’);

xold = x1;

% Iterative solution scheme

for i = 1:maxloops

% intersection of secant line with x-axis

x2 = x1 - fx1*(x1 - x0)/(fx1 - fx0);

fx2 = feval(func,x2);

fprintf(‘%3d %7.6f %7.6f \n’,i,x2,fx2);

if (abs(x2 - xold) <=tolx && abs(fx2) < tolfx)

break % Jump out of the for loop

end

if (fx2*fx0 < 0) % [x0 x2] contains root

fx1 = fx2; x1 = x2;

else % [x2 x1] contains root

fx0 = fx2; x0 = x2;

end

xold = x2;

end

321

5.4 Fixed-point iteration

g(x)atx

produces another value of x, x

, which is an improved approximation of

the root compared to the initial guess value x

. Thus,

¼ gx

ðÞ:

Again calculate the value of g(x)atx

to obtain an even better estimate of the root,

¼ gx

ðÞ:

This iterative procedure is continued until the approximation x

n þ1

¼ gx

ðÞobtained

meets the imposed convergence criteria, e.g. x

n þ1

 x

TolðxÞ and/or f (x)<

Tol(f (x)).

The ﬁxed-point iterati ve method of solution is portrayed graphically in

Figure 5.7. The pair of equations y = g(x) and y = x are plotted on the same axes.

The point (x

, g(x

)) is located on the plot y = g(x). Since g(x

)=x

, by moving

horizontally from the point (x

, g(x

)) towards the y = x line, one can locat e the

point (x

, x

). Next, a vertical line from the y = x axis to the curve y = g(x) is drawn

to reveal the point (x

, g(x

)). Again, by constructing a horizontal line from this

point to the y = x line, the point (x

, x

) can be determined. Continuing in this

iterative fashion, the ﬁnal approximation of the root can be obtained.

Figure 5.7 depicts a converging solution. However, convergence of this iterative

technique is guaranteed only under certain conditions. First, one must ascertain the

existence of a ﬁxed point in the interval of interest, and whether this point is unique

or whether multiple ﬁxed points exist. Once we know the approximate location of a

root, we need to check whether the iterative process will converge upon the root or

exhibit divergence. The following theorems are stated here without proof. Proofs can

be found in many standard numerical analysis texts (we recommend Numerical

Analysis by Burden and Faires (2005)).

If the function variable x 2[a, b], g(x) is continuous on the interval [a, b], and g

ðxÞ

exists on the same interval, then we have the following.

Theorem 5.1: If function g(x) maps x into the same interval [a, b], i.e. gxðÞ2½a; b,

then g has at least one ﬁxed point in the interval [a, b].

Figure 5.7

Illustration of the fixed-point iterative method.

Actual root

= x

, g(x

))

= g(x)

, g(x

))

, g(x

))

, x

)

, x

)

322

Root-finding techniques for nonlinear equations

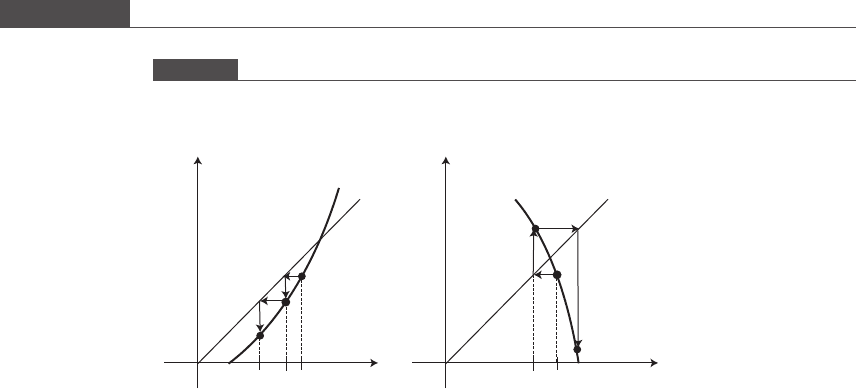
Theorem 5.2

:If0<k < 1 and g

ðxÞ

 k for all x 2½a ; b, then

(a) a single ﬁxed point exists in the deﬁned interval, i.e. the ﬁxed point is unique;

(b) for x

2½a; b the sequence x

, x

, ..., x

generated by the equation x

¼ gx

n1

ðÞ

will linearly converge to the unique ﬁxed point x*.

Note the following.

(1) Theorems 5.1 and 5.2(a) are sufﬁcient but not necessary conditions for the existence

of a unique ﬁxed point x* in the interval [a, b]. Thus, a ﬁxed point may exist in the

interval [a, b], even if g(x) maps x partly outside the interval.

(2) If k = 0, then the order of convergence is not linear but of second order. See

Newton’s method for an example of a situation where g

(x) = 0, which leads to a

quadratic convergence rate.

(3) For 0 < k <1, if C is the error constant (see Equation (5.10)), then

lim

n!∞

C ¼jg



ðÞj. Thus the smaller the value of k, the faster the rate of

convergence.

(4) If 0 < g

(x) < 1, then the convergence will occur monotonically; otherwise, if −1<

(x) < 0, the successive approximations will oscillate about the root.

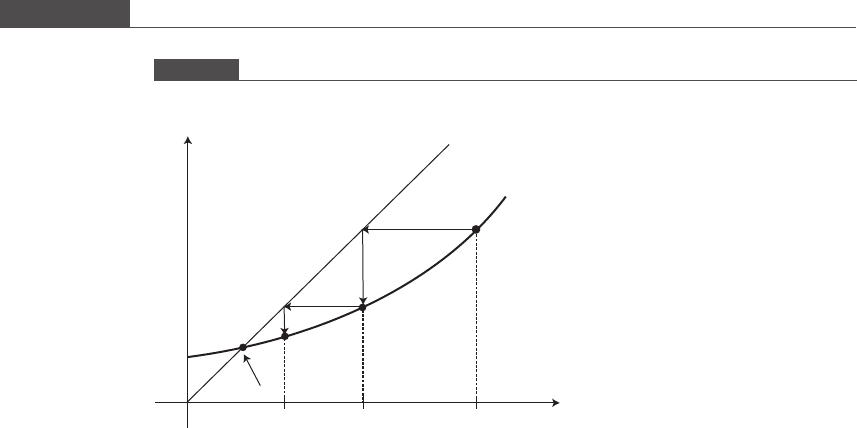
Figure 5.8 illustrates two situations where the solution technique exhibits diver-

gence. In both cases depicted in Figure 5.8, one can visually observe that |g

(x)| > 1

at all points in the interval under consideration. Figure 5.8(a) shows that when g

(x)

> 1, the solution monotonically diverges away from the location of the root, while in

Figure 5.8(b) the solution oscillates with increasing amplitude as it progresses away

from the root.

Theorem 5.2 can be easily demonstrated. Suppose gðxÞ has a ﬁxed point in the interval ½a; b. We can

write

nþ1

 x



¼ gx

ðÞgx



ðÞ¼g

ðξÞ x

 x



ðÞ;

where ξ is some number in the interval x

; x



½(according to the mean value theorem; see Section 7.2.1.1

for the deﬁnition of the mean value theorem). If g

ðxÞjjk over the entire interval, then e

nþ1

jj¼ke

and e

nþ1

¼ k

nþ1

, where e

¼ x

 x



: If k

1, then lim

n!∞

nþ1

¼ 0:

Figure 5.8

Situations where divergence is encountered when using the fixed-point iterative method to determine the location

of the root.

, g(x

))

= g(x)

(a)

y = x

(b)

, x

)

, x

)

y = g(x)

= x

, x

)

, g(x

))

, x

)

, g(x

))

323

5.4 Fixed-point iteration

Example 5.1

Consider the equation fxðÞ¼2x

þ xe

x

 4 ¼ 0, which can be expressed in the form x = g(x) in three

different ways:

x ¼ 2e

2  x



; (5:14)

x ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4  xe

x

; (5:15)

and

x ¼ 4  2x

 xe

x

þ x: (5:16)

Note that f(x) contains a root in the interval [0, 2] and thus there exists a fixed point of g within this interval.

We wish to find the root of f(x) within this interval by using fixed-point iteration. We start with an initial guess

value, x

= 1. The results are presented in Table 5.1.

Equations (5.14)–(5.16) perform very differently when used to determine the root of f (x) even though

they represent the same function f(x). Thus, the choice of g(x) used to determine the fixed point is

critical. When the fixed-point iterativ e technique is applied to Equation (5.14), cyclic divergence results.

Equation (5.15) results in rapid convergence. Substitution of the fixed poi nt x = 1.3509 into f(x) verifies

that this is a zero of the function. Equation (5.16) exhibits oscillating divergence to infinity. We analyze

each of these three equations to study the properties of g(x) and the reasons for the outcome observed

in Table 5.1.

Case A: gxðÞ¼2e

2  x



First we evaluate the values of g(x) at the endpoints of the interval: g(0) = 4 and g(2) = −29.56. Also g(x)

has a maxima of 6.0887 at x  0.73. Since for x 2½a; b; gxðÞ=2½a; b; gxðÞdoes not exclusively map

the interval into itself. While a fixed point does exist within the interval [0, 2], the important question is

whether the solution technique is destined to converge or diverge.

Next we determine g

xðÞ¼2e

ð2  2x  x

Þat the endpoints: g

(0) = 4 and g

(2) = −88.67. At x

, g

(1) = −5.44. Although g

(0.73) < 0.03 near the point of the maxima, |g

(x)| > 1 for [1, 2] within which

the root lies. Thus this method based on gxðÞ¼2e

2  x



is expected to fail.

Case B: gxðÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4xe

x

1.34 < g(x) < 1.42 for all x ∈ [0, 2]. For case B, g maps [1, 2] into [1, 2],

Table 5.1.

Iteration x ¼ 2e

2  x



x ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4xe

x

x ¼ 4  2x

 xe

x

þ x

0 1.0 1.0 1.0

1 5.4366 1.34761281 2.6321

2 −12656.6656 1.35089036 −7.4133

3 0.0000 1.35094532 12177.2917

4 4.0000 1.35094624 −296560686.9631

5 −1528.7582 1.35094626 ∞

6 0.0000 1.35094626

7 4.0000 1.35094626

8 −1528.7582 1.35094626

324

Root-finding techniques for nonlinear equations

xðÞ¼

x

ðx  1Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4xe

x

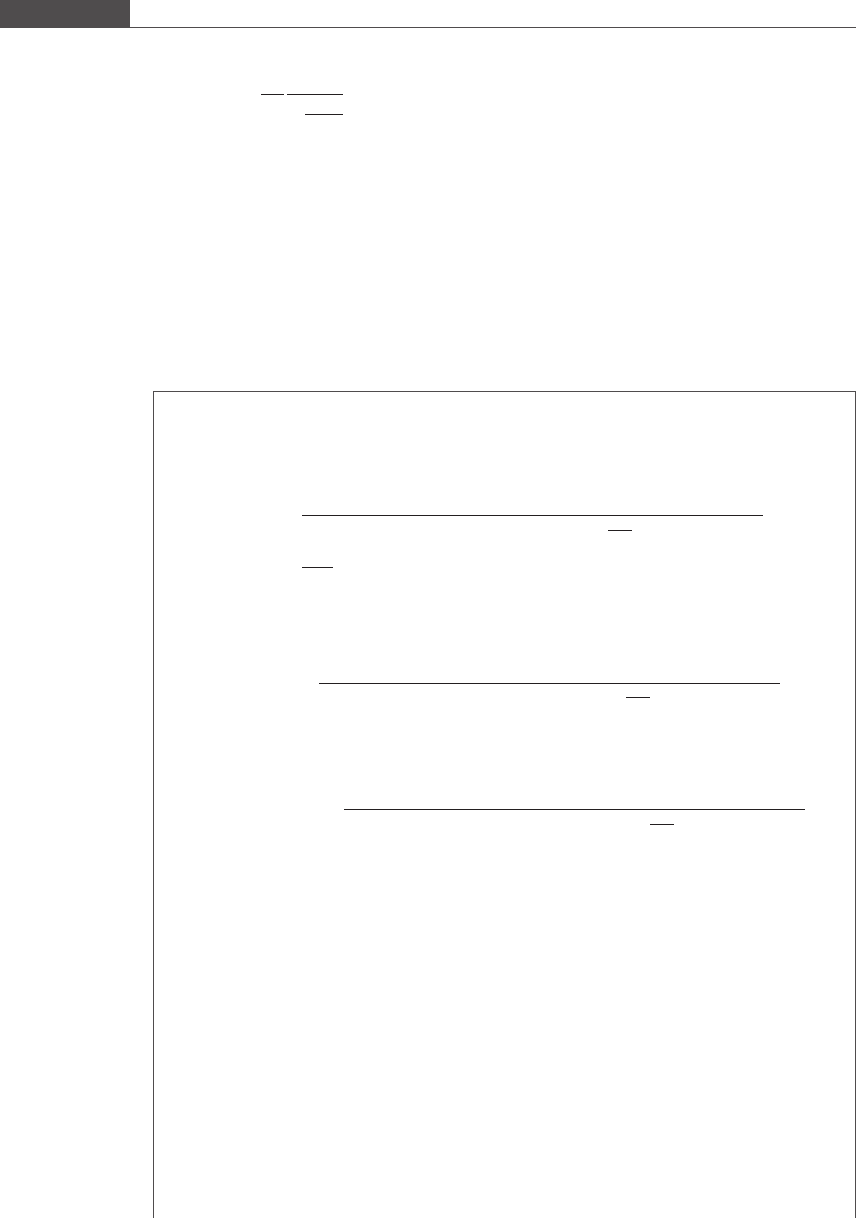
so g

(0) = −0.177 and g

(2) = 0.025. For x ∈ [0, 2], |g

(x)| < 0.18; k = 0.18, and this explains the rapid

convergence for this choice of g.

Case C: gxðÞ¼4  2x

 xe

x

þ x

For x ∈ [0, 2],  2.271 ≤ g(x) ≤ 4; g(x) does not map the interval into itself. Although a unique fixed point

does exist in the interval, because g

xðÞ¼1  4x þ e

x

ðx  1Þ¼0atx = 0 and is equal to 6.865 at

x = 2, convergence is not expected in this case either.

Box 5.1D Rheological properties of blood

We re-solve Equation ( 5.11) using fixed-point iteration and an initial guess value of 0.5:

fxðÞ¼1 þ

ð1  σ

21 σ

ðÞ

þ σ

ð1  0:070 exp 2:49x þ

1107

expð1:69xÞ



xÞ





0:44

(5:11)

Equation (5.11) is rearranged into the form x = g(x), as follows:

x ¼ 0 :44 1 þ

ð1  σ

21 σ

ðÞþσ

ð1  0:070 exp 2:49x þ

1107

expð1:69xÞ



xÞ



A MATLAB function program called ﬁxedpointmethod is written to solve for the fixed point of

gxðÞ¼0:44 1 þ

ð1  σ

21 σ

ðÞþσ

ð1  0:070 exp 2:49x þ

1107

expð1:69xÞ



xÞ



A simple modification is made to the function program hematocrit.m in order to evaluate g (x).

This modified function is given the name hematocritgx. Both hematocrit and

hematocritgx are called by ﬁxedpointmethod so that the error in both the approximation

of the fixed point as well as the function value at its root can be determined and compared with the

tolerances. See MATLAB programs 5.4 and 5.5.

MATLAB program 5.4

function g = hematocritgx(x)

% Constants

delta = 2.92; % microns : plasma layer thickness

R = 15; % microns : radius of blood vessel

hinlet = 0.44; % hematocrit

temp = 310; % Kelvin : temperature of system

% Calculating variables

325

5.4 Fixed-point iteration

sigma = 1 - delta/R;

sigma2 = sigma^2;

alpha= 0.070.*exp(2.49.*x+ (1107/temp).*ex p(-1.69.*x));% Equation5.1

numerator = (1-sigma2)^2; % Equation 5.3

denominator= sigma2*(2*(1-sigma2)+sigma2*(1-alpha.*x)); %Equation 5.3

g = hinlet*(1+numerator./denominator);

MATLAB program 5.5

function ﬁxedpointmethod(gfunc, ffunc, x0, tolx, tolfx)

% Fixed-Point Iteration used to solve a nonlinear equation in x

% Input variables

% gfunc : nonlinear function g(x) whose ﬁxed-point we seek

% ffunc : nonlinear function f(x) whose zero we seek

% x0 : initial guess value

% tolx : tolerance for error in estmating root

% tolfx : tolerance for error in function value at solution

% Other variables

maxloops = 20;

fprintf(‘ i x(i+1) f(x(i)) \n’);

% Iterative solution scheme

for i = 1:maxloops

x1 = feval(gfunc, x0);

fatx1 = feval(ffunc,x1);

fprintf(‘%2d %9.8f %7.6f \n’,i,x1,fatx1);

if (abs(x1 - x0) <=tolx && abs(fatx1) <= tolfx)

break % Jump out of the for loop

end

x0 = x1;

end

The function ﬁxedpointmethod is run from the MATLAB Command Window with the following

parameters:

function specifying g(x): hematocritgx,

function specifying f(x): hematocrit,

= 0.5,

tolerance for root = 0.002,

Tolerance for f( x) = 0.002.

MATLAB outputs

ﬁxedpointmethod(‘hematocritgx’,‘hematocrit’,0.5, 0.002, 0.002)

i x(i+1) f(x(i))

1 0.52498704 0.003552

2 0.52654981 0.000233

The solution is arrived at in only two steps, which shows rapid convergence. Note that g(x) maps the

interval [0.5 0.55] into itself and |g

(x)| at x = 0.5265 is 0.1565 while |g

(0.5)| = 0.1421. Of course

the derivative of g(x) is somewhat messy and requires careful calculation.

326

Root-finding techniques for nonlinear equations