King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

Box 4.1B Use of cyclosporin to reduce reperfusion injury during acute myocardial

infarction

The size of the infarct was estimated using MRI images from 11 patients in the control group and in

16 patients in the treated g roup 5 days after per forming percutaneous coronary intervention (PCI).

The baseline characteristics (prior to P CI) of both treated and control groups with respect to the size

of the area at risk were similar. The MRI es timates of the infarct sizes are presented below (Piot et al.,

2008):

Control Group (g) n

= 11:

20, 30, 44, 45, 46, 56, 57, 60, 65, 68, 115

Treated Group (g) n

= 16:

14, 16, 19.5, 20, 22, 23, 24, 35, 38, 38, 40, 48, 53, 64, 64, 72

It is assumed that the requirements for the Wilcoxon rank-sum test are met. The total number of

observations is n = n

+ n

= 27.

All 27 observations from the two samples are combined and ranked in ascending order (see

Table 4.18).

According to the n on-directional null hypothesis, the median infarct size of th e two groups is th e

same. If H

is true, the numbers of low and high ranks should be distributed roughly equally

between both groups. If H

is not true, then the medians of the two groups are not equal. If the

median of group 1 is larger than that of group 2, we expect more values in group 1 to be greater than

the observations in group 2. The rank sum for group 1 will be significantly larger than the rank sum

for group 2.

Since the hypothesis is two-sided, either R

or R

can function as the test statistic.

Table 4.18. Calculation of the Wilcoxon rank sum test statistic

Control Group (1) Rank Treated Group (2) Rank

20 4.5 14 1

30 9 16 2

44 14 19.5 3

45 15 20 4.5

46 16 22 6

56 19 23 7

57 20 24 8

60 21 35 10

65 24 38 11.5

68 25 38 11.5

115 27 40 13

48 17

53 18

64 22.5

72 26

Rank Sums: R

= 194.5 R

= 183.5

297

4.10 More on non-parametric tests

many ties are present, a correction term should be included in the formula used to

calculate the p value. Let’s consider a simple problem in whi ch there are two groups

of sizes n

= 3 and n

= 4. We allot seven ranks in total, one to each of the seven

observations in both groups. If the null hypothesis is true, i.e. the population

distribution is the same for both groups, each rank number has equal probability

of being assigned to either of the two groups. The allotment of three rank numbers to

groups 1 and 4 rank numbers to group 2 can be viewed as a selection process in which

any three ranks are chosen without replacement from a set of seven ranks. The total

number of distinct combinations of two sets of ranks is C

= 35.

Suppose w e have the outcome shown in Table 4.19 from an experiment. There

are three other possible rank combinations that produce a result atleast as extreme

as this, i.e. three sets of ra nks (1, 2, 3), (1, 2, 4), and (1, 2, 5) produce a value of R

≤

The probability of obtaining any of these four rank combinations is

4/35 = 0.1142. A two-sided hypothesis requires that this probability be doubled

since extre me observations observed in the reverse direction also lead to rejection

of the null hypothesis. For this example, the four extreme observations for group 1 in

the reverse direction are (5, 6, 7), (4, 6, 7), (3, 6, 7), and (4, 5, 7), which produce R

≥ 16.

The p value corresponding to the test statistic R

= 8 is 8/35 = 0.2286.

For the problem illustrated in Box 4.1, the total number of rank combinations

possible in both groups is C

. Calculation of all possible rank combinations that will

produce an R

test statistic value ≥ 194.5 is too tedious to perform by hand. Instead

we make use of statistical software to calculate the p value associated with the

calculated rank sums.

Using MATLAB

The ranksum function available in Statistics Toolbox performs the Wilcoxon rank-

sum test. The syntax is

p = ranksum(x, y)

where x and y are two vectors, not necessarily of equal length, that store the

observations of two independent samples. The p value is generated for a two-sided

hypothesis of equal population medians.

The Wilcoxon rank-sum test is mathematically equivalent to another non-parametric

statistical procedure called the Mann Whitney U test. The test procedures for either

test are slightly different but the underlying probability calculations are equivalent and

both tests yield the same p value for a given data set. The rank-sum test does not use

all the information contained in the data, i.e. the absolute magnitude of the observa-

tions are not factored into the calculation of the test statistic. Thus, this method is not

Table 4.19. Wilcoxon rank sum test

Ranks Rank sum

Group 1: 1, 3, 4 R

Group 2: 2, 5, 6, 7 R

=20

298

Hypothesis testing

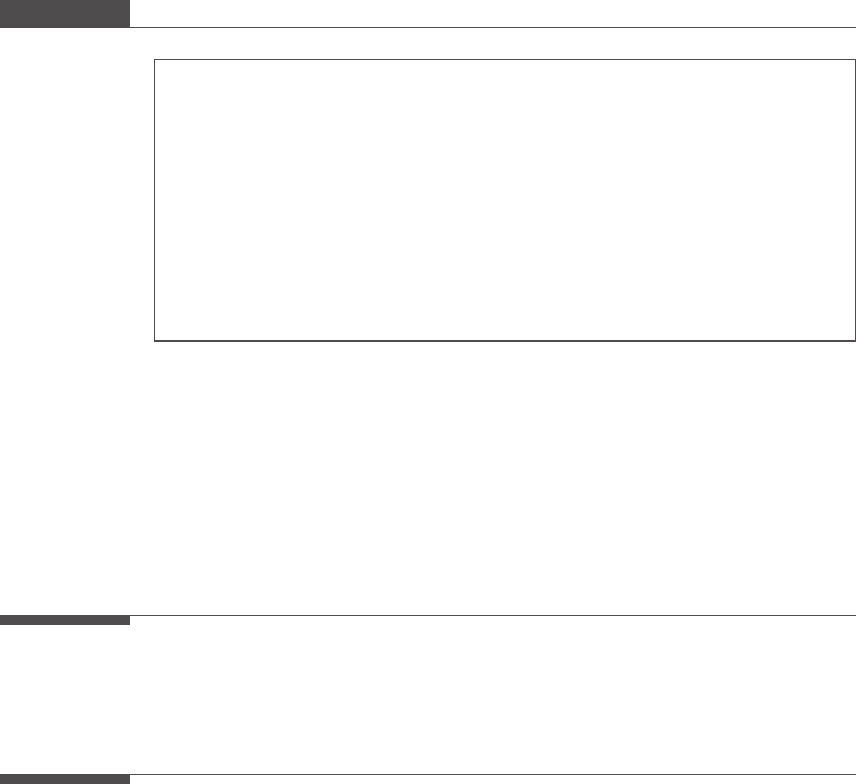
as powerful as the t test, yet it is very useful when the data distribution is far from

normal or when the data points are few in number.

Non-parametric procedures have been developed for comparing three or more

independent samples. The Kruskal–Wallis test is an extension of the Wilcoxon rank-

sum test. The parametric equivalent of the Kruskal–Wallis test is the one-factor

ANOVA. Discussion of non-parametric tests for more than two samples is beyond

the scope of this book.

4.11 End of Chapter 4: key points to consider

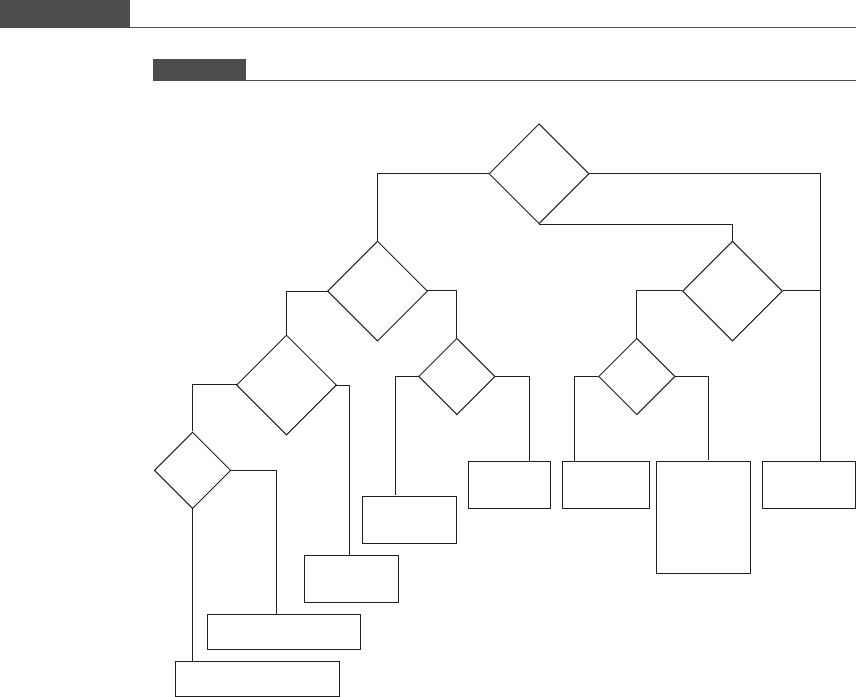
A summary of the hypothesis tests discussed in this chapter is provided as two handy

ﬂowcharts (Figures 4.14 and 4.15) outlining the criteria used to select a hypothesis

test for (1) cardinal data and (2) nominal data.

4.12 Problems

4.1. Statistical tests. Match up the following studi es with the most appropriate

statistical test.

Are three sample means different from one another? H

: μ

= μ

Compare the mean rolling velocity of 2500 leukocytes at a low ﬂuid shear rate,

with the mean rolling velocity of 3000 leukocytes at a high ﬂuid shear rate.

Compare the red blood cell counts of 20 patients before and after treatment with

erythropoietin.

When do ﬁbroblasts stop spreading on ﬁbronectin? Compare the average area of

12 cells at t = 30 min with the ave rage area of 10 cells at t = 120 min.

Mortality rates of different groups of leukemic mice are presented in a 4 × 2

contingency table. Test for differences among the populations.

(A) Two-sample z test.

(B) Paired t test.

(D) χ

test.

(E) Analysis of variance.

4.2. Treatment of Kawasaki disease using pulsed corticosteroid therapy Kawasaki

disease is most common in young children and is characterized by inﬂammation of

the arteries, skin, and mucous membranes. This disease is responsible for causing

Box 4.1C Use of cyclosporin to reduce reperfusion injury during acute myocardial

infarction

The p value is calculated using the MATLAB ranksum function:

x = [4.5 9 14 15 16 19 20 21 24 25 27];

y = [1 2 3 4.5 6 7 8 10 11.5 11.5 13 17 18 22.5 22.5 26];

p = ranksum(x, y)

0.0483

The test statistic reaches significance for a significance level set at α = 0.05. We conclude that the

median infarct sizes for the treated and control groups are different.

299

4.12 Problems

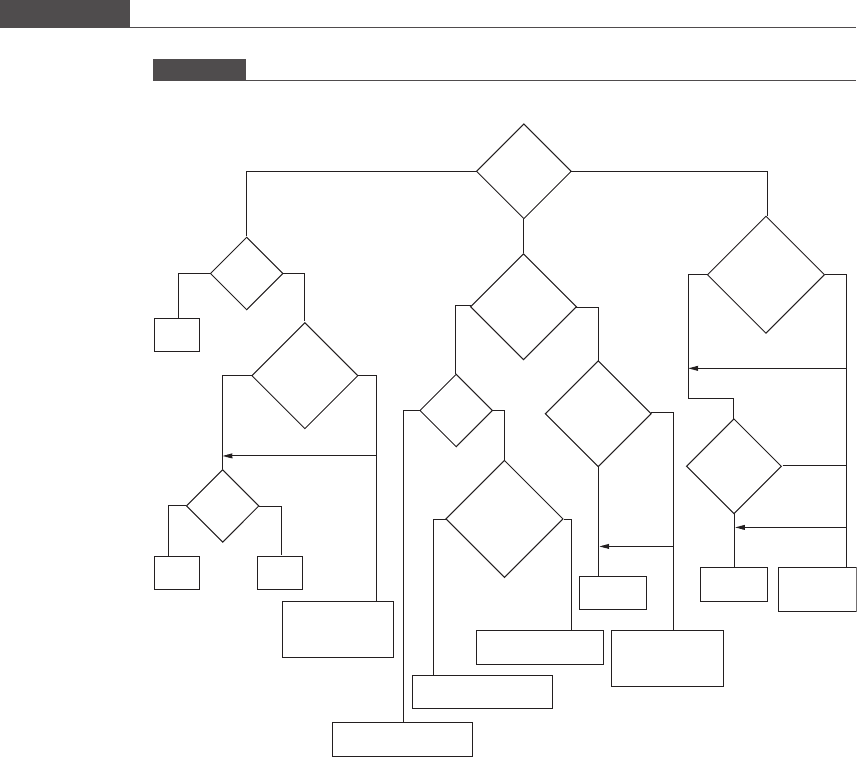
coronary artery aneurysms. Standard treatment of Kawasaki disease consists of

administering intravenous immunoglobulin and aspirin. Despite treatment, a small

percentage of the children still develop aneurysms. A double-blinded, placebo-

controlled clinical trial was conducted in eight centers in North America to study

the beneﬁts of including corticosteroid therapy (intravenous methylprednisolone)

with conventional treatment for preventing the development of aneurysms

(Newburger et al., 2007). Two-dimensional echocardiography was used to measure

the internal diameters of several coronary arteries. The lumen diameters were stand-

ardized using body surfa ce area and converted to z scores. The mean maximum z

score after 5 weeks of administering methylprednisolone was found to be 1.31 ±

1.55 for 95 patients in the treatment group and 1.39 ± 2.03 for 95 patients in the

placebo group. Use the two-sample t test to determine if methylprednisolone is

effective in reducing the arterial diameter. First, construct the null hypothesis.

Next, calculate the standard error of the null distribution of the test statistic.

Calculate the test statistic and draw your conclusion based on the corresponding p

value.

4.3. Treatment of skeletal muscle injury using angiotensin II receptor blocker In the

study of the effects of angiotensin receptor blocker (ARB) on the healing of skeletal

muscle (Box 4.2), the extent of muscle ﬁbrosis was measured 5 weeks after injury.

Figure 4.14

Hypothesis test selection criteria for cardinal data.

No. of

samples?

population

distribution

normal?

Are

population

equal?

n large?

Independent samples

z test

yes no

Wilcoxon rank-sum

test

Wilcoxon signed-

rank test

or sign test

n large?

> 2

yes

Kruskal–

Wallis test

z test

yes

σ known?

noyes

z test t test

transform data

Are

samples

independent?

noyes

yes

Are

popula-

tions normally

distributed?

Independent samples

t test

yes

distribu-

tion of d

’s

normal?

paired t

test

transform

data

Wilcoxon signed-

rank test

or sign test

Are

popula-

tions normally

distributed?

yes

transform data

ANOVA

yes

transform data

300

Hypothesis testing

The mean areas of ﬁbrosis within the injured zone observed in the three groups after

5 weeks are

control group: 45% ± 22%, n

=5;

low-dose ARB group: 19% ± 9%, n

=8;

high-dose ARB group: 14% ± 11%, n

=7.

You are asked to determine if administration of low-dose and high -dose ARB drug

(losartan) reduces ﬁbrosis of skeletal muscle in mice. Using the two-sample (non-

directional) t test for unequal variances, compare the mean area of ﬁbrosis within the

injured skeletal muscle:

(1) between the control group and the low-dose ARB group and

(2) between the control group and the high-dose ARB group.

4.4. In vitro fertilization (IVF) treatment Box 4.7 highlights the study performed by

Malizia et al.(2009) to determine the cumulative live-birth rates resulting from

IVF treatment over a course of six cycles. In Box 4.7, a comparison of population

proportion of live births for two different age groups was performed when an

optimistic approach was adopted to account for the outcomes of non-returnees

in the cohort. Here, we look for differences in population proportions of

live births within the age groups when a conservative approach is used, i.e. all

Figure 4.15

Hypothesis test selection criteria for nominal data.

No. of

samples?

No.

of nominal

variables?

No.

of catego-

ries k?

z test for one population

proportion

yes

binomial distribution

> 2

n large?

Fisher’s

Exact test

yes

> 2

one nominal variable

No.

of catego-

ries k?

> 2

test of

homogeneity

or z test

for two

population

proportions

n large?

yesno

Fisher’s 2

x 2

Exact test

one nominal variable

test of

homogeneity

test of

independence

goodness-

of-fit test

n large?

301

4.12 Problems

non-returnees to subsequent IVF cycles (i.e. cycles 2 to 6) are assumed to have failed

outcomes.

The conservative cumulative probabilities for live births observed at the end of

each IVF cycle are displayed in Table P4.1. The cohort is divided into four groups

based on maternal age. The cohort of 6164 women is categorized according to age as

in Table P4.2.

Determine at the end of the sixth IVF cycle whether the probabilities of live births

for the age groups of less than 35 years of age and equal to or more than 35 years of

age are signiﬁcantly different.

4.5. The independent-samples t test for equal variances is related to the F test (one-way

ANOVA) by the following simple relationship: the square of the t statistic is equal to

the F statistic, i.e.

¼ F:

The t statistic is calculated as

t ¼







ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

pooled



;

where

pooled

 1ðÞs

þ n

 1ðÞs

þ n

 2

If the two sample sizes are equ al to n, then

t ¼







pooled

ﬃﬃﬃﬃﬃﬃﬃﬃ

2=n

and s

pooled

þ s

Table P4.1. (Conservative) probability of live birth

Maternal age (years)

IVF cycle <35 35 to <38 38 to <40 ≥40

1 0.33 0.28 0.21 0.09

2 0.49 0.44 0.32 0.15

3 0.59 0.51 0.40 0.19

4 0.63 0.55 0.43 0.21

5 0.65 0.56 0.45 0.22

6 0.65 0.57 0.46 0.23

Table P4.2.

Age Number of individuals

<35 2678

35 to <38 1360

38 to <40 836

<40 1290

302

Hypothesis testing

Accordingly,







ðÞ

pooled

Show that the F statistic calculated for two independent samples drawn from

normally distribut ed populations with equal variances reduces to the equation

above for t

4.6. Suppose that you want to test for differences in the deformability of red blood cells

among four different age groups of people. Thus, the null hypothesis is:

= μ

How many pairwise t tests would be necessary to test all possible differences? If we

want to set the overall probability for making a type I error at 0.10 (10%), what

should the level of signiﬁcance be for each individual t test using the Bonferroni

adjustment?

4.7. In Box 4.8 we used the MATLAB multcompare function to determine which

groups’ means are signiﬁcantly different from each other. The default multiple com-

parison procedure ‘tukey-kramer’ was used. Perform the comparison again using

the other three comparison procedures ‘dunn-sidak’, ‘bonferroni’,and

‘scheffe’ available in MATLAB. Do any of these three procedures ﬁnd additional

signiﬁcant differences between group means that the Tukey–Kramer method did not?

Also, do other procedures also ﬁnd groups 1 and 4 and groups 3 and 4 signiﬁcantly

different? What can you say about these three multiple comparison procedures? Are

they each more or less conservative than the Tukey–Kramer method?

4.8. Weight gain from type 2 diabetic treatments Type 2 diabetes mellitus is also

termed as the “insulin resistance” disease because the problem lies not with the

production of insulin, but with the signal transduction process within cells that

respond to insulin. Insulin binds to receptors on cell surfaces to promote uptake of

glucose for various purposes, such as production of glycogen and fat (in adipocytes

and hepatocytes), and conversion of glucose into energy (in myocytes). Decreased

sensitivity of these cells to insulin will result in reduced transport of glucose from

blood into the cells resulting in hyperglycemia. This disease is managed with anti-

diabetic drugs that work in a variety of ways, such as by suppressing the producti on

of glucose in the liver, by increasing insulin sensitivity, and/or by promoting insulin

release from the pancreas. When blood sugar cannot be controlled by using anti-

diabetic drugs and strict diet and exercise, insulin may be prescribed. Insulin intake is

accompanied by side-effects such as hypoglycemia and weight gain. Three different

insulin + anti-diabetic oral drug therapies are compared with respect to a number of

outcomes including weight gain. At baseline, the adult patients recruited to the study

were not treated with insulin previously. The weight gain observed after one year of

therapy is presented in Table P4.3. Determine whether the diabetic treatments

produce differential weight gain in the patients. Formulate the hypothesis and test

it using the one-way ANOVA. Calculate the F ratio and use the fcdf function to

calculate the p value. Use the anova 1 function to check your result. What are your

conclusions?

4.9. Inheritance of Huntington’s disease Huntington’s disease is a neurodegenerative

hereditary disorder characterized by loss of limb and muscle coordination and

decline in mental abilities. The disease is caused by a mutation in the Huntingtin

303

4.12 Problems

gene that encodes for an abnormal protein, which interferes with brain functioning.

This autosomal (not linked to sex genes) disease is inherited by children from parents

in a dominant fashion. Thus, if a person is heterozygous with one copy of the

mutated gene, he or she will present the disease. A person having one copy of this

gene will pass on the disease with 50% probability to each child that he or she has

with an unaffected person. In other words, the offspring have a 50 : 50 chance of

inheriting the gene and therefore the disease. Table P4.4 explains the Mendelian

inheritance of the genes, where H is the normal allele of the gene and H

is the

mutated allele of the gene that pro duces the disease.

A person with the HH

pair is heterozygous with one copy of each allele and will

develop the disease.

A study is conducted to conﬁrm that the disease is indeed passed from generation

to generation according to Mendeli an rules of complete dominance. A total of 120

couples are selected such that only one partner is heterozygous with a single copy of

each allele, while the other has only the normal alleles. Out of 217 children of the 120

couples, 122 developed the disease. Use the χ

goodness-of-ﬁt method to determine

whether the observations support the null hypothesis of complete dominance of the

mutated Hunti ngtin gene.

4.10. Distribution of birthweights in two different racial groups in England and Wales In

Box 4.10 we used the χ

goodness-of-ﬁt test to determine if the birthweigh t distri-

bution among the White British population in England and Wales is normally

distributed. We found that the birthweight distribution was negati vely skewed.

You are asked to use the χ

goodness-of-ﬁt test to determine if the birthweight

distribution among the British Indian population is normal. Prepare a table similar

to Table 4.9 and report the relevant test statist ic and corresponding p value. What

are your conclusions?

4.11. Administering modaﬁnil to alleviate night-time sleepiness in patients with shift-work

sleep disorder In Example 4.8, a study (Czeisler et al., 2005) that examines the

efﬁcacy of using modaﬁnil to treat patients suffering from chronic sleepiness at night

Table P4.3.

Weight gain (kg)

Patient Treatment 1 Treatment 2 Treatment 3

1 13.5 −0.7 0.1

2 6.9 16.8 9.0

3 4.2 7.6 13.2

4 9.6 4.4 7.9

5 −7.6 7.6 10.5

6 5.5 3.9 9.0

7 3.2 4.2 4.3

8 −3.6 10.7 7.1

9 0.1 10.3

10 3.3 10.4

11 7.4

304

Hypothesis testing

during night-shifts at work was discussed. Following treatment with modaﬁnil, the

number of pa tients in both control and treatment groups that reported accidents or

near-accidents during their travel from work to home afte r a night-shift was

recorded and is given in Table P4.5.

Prepare a 2 × 2 contingency table for the frequency of patients that underwent

an accident or close-encounters when returning home from work for both the treat-

ment and control groups. Is the proportion of accident-prone patients different in

the treated group versus the control group? Did the use of modaﬁnil make a

difference?

4.12. Wearing of Hylamer polyethylene hip-joint components Hip-joint implants were

synthesized from Hylamer polyethylene in the 1990s. Hylamer is a modiﬁed version

of ultra-high molecular weight polyethylene (UHMWPE) manufactured

by DuPont. Components made from this material are prone to increased wear

and tear if sterilization using gamm a rays is performed in the presence of air. Wear

of prosthetic implants generates debris causing loosening of the implant compo-

nents, a phenomenon called periprosthetic osteolysis. A 2005 orthopedic study in

Bologna, Italy (Visentin et al., 2005) characterized the polyethylene particulate

matter generated from both (1) Hyla mer components and (2) traditi onal

UHMWPE synthesized components, gamma sterilized with O

present. The mor-

phology of the particles was studied using a scanning electron microscope. The

Table P4.4. Punnett square

Parent 1

HH’

Parent 2 H HH HH’

H HH HH’

A Punnett square is a diagram that lists all the possible combinations

of two alleles, one of which is obtained from the mother and the other

from the father. One of the listed combinations is inherited by each

offspring. Using a Punnett square, one can calculate the probability of

observing a particular genotype (and phenotype) in the offspring.

Table P4.5.

Modaﬁnil-

treated group,

Placebo

group,

=96 n

= 108

Number of patients that experienced an accident or

accident-like situation while commuting from work to

home

28 58

305

4.12 Problems

distribution of granular particles (aspect ratio ≤ 2) and ﬁbrillar particles (aspect

ratio > 2) in both groups is presented in Table P4.6.

Is the particulate nature of the wear particles for Hylamer PE different from that

of traditional UHMWPE? Formulate a null hypothesis. Which test will you use to

test your hypothesis? What is the p value associated with your calculated test

statistic? What are your conclusions?

4.13. Rise of multidrug-resistant streptococcus pneumoniae in the USA The Active

Bacterial Core Surveillance program of the Centers for Disease Control and

Prevention published an epidemiological study (Whitney et al., 2000) on the trends

in antibiotic resistance of S. pneumoniae strains that cause invasive pneumococcal

infections (e.g. meningitis and bacteremia). A pneumococcal disease is considered

invasive if the bacteria enters and colonizes in otherwise sterile body regions such

as blood, joints, and cerebrospinal ﬂuid. A large sample of patients was selected

from various regions across the USA (Portland, Oregon; San Francisco County,

California; greater Minneapolis and St. Paul; greater Baltimore; greater Atlanta;

Tennessee; greater Rochester, New York; and Connecticut).

The incidence of penicillin-resistant pneumococcal infections among various age

groups is given in Table P4.7.

Determine whether penicillin-resistant S. pneumoniae infections are equally

prevalent among all invasive pneumococcal infected age groups.

4.14. Neurostimulation as a treatme nt option for Parkinson’s disease In Box 4.11,a

study on using deep-brain stimulation to sympt omatically treat Parkinson’s disease

was outlined. In this study (Deuschl et al., 2006), the severity of motor symptoms,

measured using the Uniﬁed Parkinson’s Disease Rating Scale, was compared pair-

wise between patients receiving neurostimulation and patients when they were not

on any medication. Among 78 pairs of patients, 55 pairs of neurostimulated patients

fared better, and 21 pairs demonstrated that non-medicated patients had a better

outcome. The outcome was the same for two pairs. Test the hypothesis that the

Table P4.6.

Hylamer PE inserts UHMWPE inserts

Granules 318 123

Fibrils 509 149

Table P4.7.

Age (years)

<5 5–17 18–64 ≥65

Penicillin-resistant infections 295 22 282 240

Penicillin susceptible infections 620 83 1179 753

306

Hypothesis testing