Капутин Ю.Е., Ежов А.И., Хейнли С. Геостатистика в горно-геологической практике
Подождите немного. Документ загружается.

4.3.3.
При
ведение
моделей
"
точечному
ВИДУ
(~гулярнзацня)
Всс
экспернмент:шъные
вариогрnммы
строятся
на
пробах,
имеющих
объем,
отличный
01'
точки
.
Иногда
приходится
обрабатывать
данные
нескольких
видов
опробовuния
с
разными
размерами
проб.
В
последующих
расчетах
~Iaще
всего
приходится
распространять
свойства
модели
на
самые
различные
объемы
руды
и
породы.
Между
тем
ИЗDестно,
что
форма
и
параметры
нариограммы
тесно
связаНbJ
с
ра:!мерамн
оснавnния
(блока
или
пробы, для
которых
делаетсн
оценка)
(
Рис.4.10)
.
Для
сравненин
и
объединения
результатов
необходимо
исключить
ВJНшние
на них
объема
проб
,
Т
.
е.
привести
модели
к
точечному
ОСНОDанию.
Эта
стuдия
изучения
массива
также
Яf1ЛЯется
обязательной,
ссли
нельзя
бе
з
серьезного
искажения
результаТ08
допустить,
что
полученную
нами
модель
можно
признать
точечной.
Все
последующие
эт
а
пы
'
геО
,
статистического
исследования
используют
вариограммную
м
о
дель
ТОЛЬКО
на
точечном
основании
.
Р
а
зличают
2
наиболее
простых,
но
часто
встречающихся
случан
регуляризации:
1)
месгоро
х
<Дение
разведано
пробами
одинаКОDОЙ
длины
(1);
2)
рассматривается
слой
(или
пласт)
одинаковой
мощности
(1).
"7
С
Cl
r-
__
___
~~
--
~--~--~----------~~
2
л
-
а
--
'
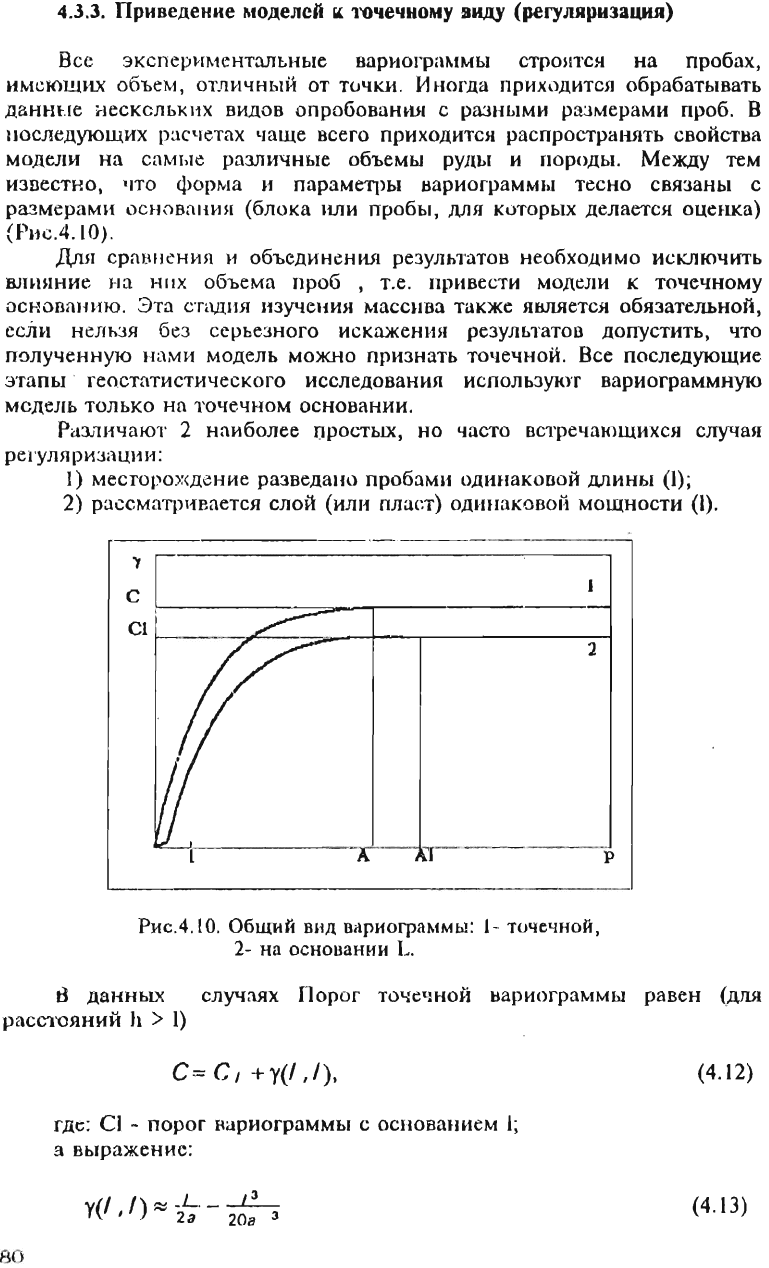
Рис.4
.
10
.
Общий
вид
nариограммы:
1-
точечной
,
2-
на
основании
lJ.
р
в
данны
х
случаях
Порог
точечной
вариограммы
равен
(для
р
а
сстояний
11
>
l)
80
С=
с
I
+y(/,/),
где
:
CI
-
порог
Rар"юграммы
с
основанием
1;
а
выражение:
у
(
l
I)~_L_~
,
2а
20а
3
(4.12)
(4.13)

Зона
ТО'l
е
4110Й
ваРИОI
'
раммы
для
проб
одной
длины
paBH~
А
=
А
/ - 1,
(4
.
14)
а
для
пла
с
тов:
А
=
А
/ (4.15)
Т
ака
я
аппроксима
ция
дает
ошибку
не
более
10
%
в
н
а
иб
ол
е
неблагоприятн
ом
случае и
менее
1 %
в
основных
ситу
ациях
,
встречающ
ихсSl
"а
прапике
(т
.
е.
при
h >
31
и
при
любом
соот
н
о
ш
еНИ
II
IjA)
4
.3.4.
ПР
ОСТ
Рitн
ствеJIНая
модель
вариограммы
По
с
ле
получ
е
ния
набора
экспериментальных
вариогр
а
мм
ДТlЯ
основны
х
напрам
е
ний
ан
и
зот
ропии
ма~сива
и
приведеНI1Я
его в
соответствие
с
реальной
геологичес
кой
картиной
месторождения
необходимо
создать
и
з
этих
составляющих
единую
3
-
х
мерную
пространс
твеllНУЮ
вариограммную
модель
.
Эта
модель
будет
участвовать
во
всех
последующих
г
еоста
т и
стических
р
а
сч
ет
ах
И
поэтому
должна
быть
максимально
коррек
тна.
В
.
общем
с
л
учае
модель
месторождения
может
состоять
и
з
и
з
отропны
х
и
аJiИ
З
ОТРОПНЫХ
составляю
щих.
Различают
геометрическую
и
з
он
альную
анизотропи
ю
(См
.
главу
3).
Второй тип
связан
с
наличием
на
м
есторождении особых
структур
и
з
менчивости,
каждая
из
которы.х
в
свою
очередь
может
иметь
с
вою
геометрическую
анизотропию.
Геом
ет
рич
ес
к
а
я
анизотропия
чаще
всего
используется
на
практике
и
предполага
ет,
ч
то
вариограммная
модель
в
разных
направлениях
имеет
р
азл
ичны
е
зоны
влияния,
но
одинаковый
порог,
и
ее
можно
превратить
в
и
отропную
мод
ел
ь
простым
преобразованием
координат
.
В
компьют
ерных
систе
м
ах
и
прогр
а
ммах
чаще
всего
используется
геометрическая
ани
з
отро
пия
,
а
также
следующие
принципы
описания
пространствеННblХ
вариограммнbIX
моде
лей.
В
се
параметры
ДJlЯ
каждой
модели
могут
быть
анизотропны;
Т
.
е
.
они
могут
им
еть
р
азл
ичны
е
значения для
различных напраменИ:Й
.
'
В
случае,
когда
а
низотропия
у
с
таномена,
должны
быть
определены
три
взаимно
перпендикулярных
напраW1ения,
соответствующих
главным
осям
пространственного
эллипсоида
анизотропии
.
Длина
осей
эллипсоида
в
каждом
напрамении
представляет
собой значение
зоны
МИЯНИЯ
.
(или
другого
пар
а
метра)
в
это
м
направпении
.
Предполагuется
,
что
гл
ав
ны
е
оси
ани
з
отропии
им ют
те
ж
е
направления
ДТIЯ
каждого
параметра
вариограммы,
но
ко
фф
ициенты
анизотропии,
определенные
к ак
отноше
н
ия
длин
дв
у
о
с
ей
ЭJU
1Ип
с
оида
,
могут
бьrrь
р
азл
и
lными
ДТlИ
р
аЗllЫ
п
а
рам
е
тров
.
П
осл
е
доват
е
льн
с
ть
СОПО
С
Т:lWlеJlИЯ
используе
мой
прям
о}'!
'
льной
си
с
т
е
мы
к
о
ордин
а
т
осями
про
с
тра
н
стве
нн
ого
.
лл
ип
соида
ШIИ
ОТ
Р
О
IIIЩ
ПРl\
о~де
н
lIиж
е
:
(Ри
.4. J t ).
81

а)
.
z=z'
у'
1.
ПCJЮDOГ
на
утоо
1
1ЮКDYГ
сси
Z
2.
Пaoopor
на угоо
2
QOКpyr
ССИ
Х'
А
-
ОСь
направления
1
В
-
0С1.
нarJpa1)neния
2
С
-
ОСь
направления
3
с)
Z·=C
·
в
у'
А
З.
I1aoopoт
на
У!ОО
3
ocacpyt
·
сси
Z"
Рис.
4.
11
.
Попорот
осей
координат
к
эллипсоиду:
а
-
угол
Р
,
Ь
-
угол
Q,
с
-
угод
G .
1.
Сначала
предположим,
что
оси
эллипсоида
А
,
8
и
С
параллельны
соотв
ет
ственно
У,
Х,
11
' Z
оснм
прuвосторонней
системы
координат.
2.
Затем
поворачиваем
систему
координат
пр
оти
в
часовой
стрелки
(если
смотреть
в
положительном
направлении
оси
Z)
на
угол
Р
(р=о
-
90
градусов)
вокр
уг
оси
Z. .
3.
Затем
поворачиваем
сист
ему
координат
на
угол
Q (Q=0-90
I
'
paдycoB)
против
часовой
стрелки
вокруг
"новой"
оси
Х
,
Таким
образом
можно
двумя
углами
(Р
и
Q)
задать
практич
ески
любую
ориен
та
цию
пространственного
э
ллипсоида.
.
4 ..
Если
необходимо,
то
можно
р
азвернугь
систему
е
ще
на
один
угол
(О)
против
часовой
стрелки
вокруг
"новой"
оси
Z.
Таким
образом
можно
совместить
используемую
нами
систему
координат
с
основными
напр
авле
ниями
анизотропии
массив
а,
ч
т
о
необходимо
для
дальнейших
геост
ат
истиче
ских
р асч
етов.
Направл
ен
ия
всех
поворотов
указаны
верно,
если
смотреть
в
положительном
направлении
оси
поворота.
Параметры
вариограммы
определяются
ДJ1H
каждой
оси
эллипсоида:
А,
В
и
С.
Чтобы
вычислить
значе
ния
п
а
р
аметра
в
D
направлении,
которое
не
паралл
елъно
ни
одн
ой
нз
.
трех
осей
,
уравнение
эллипсоида
р
е
шают
вместе
с
уравнением
Пр$
мой,
проходящей
через
центр
эллипсоида
в
направл
е
нии
О
.
Расстояние
между
центром
элл
ипсоид
а
н
его
поверхностью
в
данном
направлении
пре
дставляет
собой
требуемое
значение
параметр
а.
Ниже
ЛРИl:lсдены
основны
ИСЛО
ь
уемые
в
компьютерных
расчетах
лространс
тве
нные
модели
вариограмм
и
парiЗМетры,
тр
еб
уемые
для
их
однознnчного
ОIН1сания
.
8 2

Одноструктурная
сферическая
модель
0(1\)
=
Со
+
С
(1.511ja -
0.5(11jа)**З)
при
h <
а
=
Со
+
С
при
h
=>а
Требуются
12
пnраметров:
р
1
>ЭФФскт
амородков
(Со)
для
оси
А
Р
2>"
(
о)
для оси
В
р
3>"
(Со)
для
оси
С
р
4>
РаЗНllца
между
порогом
вариограммы
и
Со
(Сl)
для
оси
А
Р
5> -"- " " "
в
Р
6> -"- " " "
С
Р
7>30на
ВЛИЯllия(А)
для
оси
А
Р
8>"
"
в
Р
9>"
"
С
РI0>Угол
поворот
а
эллипсоида
Р
(0-90
градусов)
Рll
>Уг
ол
поворота
элли
псоида
Q (0-90
градусов)
Р12>Угол
поворота
эллипсоида
О
(0-90
градусов)
Двухструктурная
сферическая
модель
0(1\) =
Со
+ 01(1\) + 02(11),
где:
01(1\) =
CI(I.5/al
-
О
.
5(Ь/а1)**3)
при
11
<
аl
=
С1
при
h
=>
аl
02(1\) =
С2(
1.5/а2
-
0.5(11jа2)**З)
при
h <
а2
. =
С2
при
h = >
а2
Требуетсн
18
параметров:
(в
каждой
группе':'
3
параметра
для
осей
;
А,
В,
С)
Р
l-РЗ>Эффект
самородков
(Со)
для
осей
А,В,С
Р
4-Р6
>
Разница
между
порогом
первой
структуры
вариограммы
и
Со
-
(CI)
Р
7-Р9>30на
ВЛИЯНИЯ
(Al)
для
первой
структуры
PlO-Р12>
Разница
между
порогом
второй структуры
вариограммы
и
(Со+С1)
-
(С2)
РIЗ-РI5>30на
влияния
(А2)
для
второй
структуры
Линейная
модель
О(1\)
=
Со
+
S*'1
Р
l
-
РЗ
>Эффект
самородков
(Со)
Р
4-Р6>Тангенс
угла
наклона
вариограммы
(S)
PI6-РI8>Углы
поворота
эллипсоида
P,Q, 0 .(0-90
градусов)
МодеJ."
Де
Вийса
0(11) =
Со
+ S*IOg(ll)
Р
l-РЗ
>
Эффект
самородков
(Со)
р
4-Р6
>Та
нгенс
угла
наклона
варио
грам
мы
(S)
PI6
-
РI8>УГJlЫ
поворота
эллипсоида
P,Q, G
(0-90
градусов)
Аналогично
определяются
параметры
пространственных
моделей
Гаусса
и
ЭКСllоне.щиал
..
ноЙ
.
Экспериментальная
модель
Иногда
пользователь
н
е
может
подобрать
к
полученной
Rариограмм
е
ни
одну
из
стандартных
моделей.
Несмотря
на
определ
е
нн
у
ю
"паСНОС
'
IЪ"
такого
шага
труднопредсказумыми
83

последствиями,
он
тем
не
менее
может
сделать
свюю
вариограмму
моделью
и
-
задать
ее
следующим
способом.
Модель
может
быть
определена
по
18
экспериментальным
точкаt.t
.iJ.Jш
каждого
и~ трех
направЛений
.
Требуемые
параметры:
.
р
1>ЧИСJ10
точек,
по
которым
приводятсн
значеНl1Я
-
р
2>Угол
поворота
эллипсоида
Р
(0-90
градусов)
р
з>)'гол
ПОБОрОта
эллипсоида
Q (0-90
градусов)
р
4>Значение
расстояния
ДЛJI
первой
точки
р
5-Р7>Значение
вариограммы
дня
перnой
точки
р
8>Значение
расстояния
дЛЯ
ВТОРОЙ
точки
Р
9-
Р
11>
Зна'lение
baPl-юграммы
для
ВТОРОЙ
точ,,:и
и так
до
максимума
Р72>Значение
расстояния
ДJШ
18
точки
P73-Р75>Значение
вариогрuммы
для
18
точки
.
Для
определения
значения
вариограммы
между
экспериментальными
точками
8
данном
направлении
в
программе
используется
линейная
интерпоJUЩИЯ
.
З'
-
I:l'1ение
Вllриограммы
для
р аССТОJIНИЙ
,
меньших
чем
пероая
точка,
устанавливается
равным
эксперимеНТQJ1ЬНОМУ
значению
для
первой
точки.
След
о
вате4ЬНО,
лучшее
знаLIение
расстояния
для первой
точки
есть
О
.
Значение
вариограммы
ДJШ
РnССТШlНия
большего,
чем
максимальное
значение
для
последней
точки
устанавливается
равным
значению
вариограммы
для
последней
точки.
Многоструктурная
сфериt.еская
модель
Наличие
анизотропии
в
"эффекте
самородков"
и
основных
пар:\метрах
моделей
вариограмм
может,
прн
определенных
условинх,
привести
к
таким
проблемuм,
как
uтрицательнаJ1
дисперсия
кригинга,
и
получению
оценок,
существенно
меньших
или
больших
чем
исходных
величины
данных,
по
которым
ВЫllолнuется
оценка
.
Один
нз
способов
устраненин
этих
проблем
-
это
разделение
исходной
В1.\риогрпммноЙ
мо
де
ли
на
серию
составляющих
,
каждая
из
которых
должна
иметь
собственное
значе'fI1е
дисперсии
с
аннзотропиеи
из
разрешенного
диапазона
.
Вnриограмма
данной
модели
ра
'
зрешает
ИСПОЛl
.зо
вать
до
7
сферических
структур,
КО
ТО
РЫ
е
ВЫ'lИсляют
я
как
:
0(11) =
Со
+
Сl
•
(1.511/1.\
1 - 0.5(II/a 1
)НЗ)
+
С2
•
(.1
.
511/з2
- 0.5(11/
2)·*З)
+
С3
*
(1.511/1.\3
-
0
.
5(h/аJ)··З)
+
С7
*
(l
.
511/а7
- 0.5(11/117)*·3
Номера
требу
мых
парамеТРО8
(NP)
заnИСRТ
т
номера
структуры
модеШ1
(NS)
:
84
NP
= 4 + 4
,..
NS
Требуемые
параметры
:
р
1>
КОЛИ'lеСТDО
структур
(минимум
1,
м
а
ксимум
7)
р
2>Эффект
самородков
(Со)

Р
3>
Р
i
шюсl'Ь
между
lIoporOM
)
структуры
и
Со
( I
)(I1'JOTonHaJl)
Р
4
-Р6
>
Зона
WIШIНШI
первой
структуры
для
3-х
осей
р
7>
Ра
з
нос
т
ь
между
порогом
2
структуры
и
(
о+С
1
)-(С2)
(изотопная)
Р
8-
PIO
>
01Ja
l1JНIНIII1Я
втор
Й
структуры
для
3-х
о
ей
......
.,
...
......
.....
...
.
...
.......
....
.......
..
........
.
...
.
....
..
............
.
....
.......
.....
...
..
..
.
..
.......
.
Р??
>
УГОJl
поворота
ЭJUlИГIСОllДа
Р
(0-90
градусов)
P?'l
>
Угол
повор
>1''''
ЭЛЛ
ИПСОI1Дn
Q (0-90
градусов)
P??
>
YI
'
OJl
новорол\
ЭЛJ1l
1lJСОН
Щ
\
G (0-90
l
'
Раду
'ОВ)
4.3.5.
НадеЖIШСТа.
модеJlей
вариограмм
(робаСТtIЫ~
методы
оцеlшвания)
.
При
н
е
возможно
VI
'
И
ис.:пользования
ГИlJOтс:зы
стацион
рtЮСПI
применителыю
к
исследуемому
массиву
обычный
расчет
ваРИОГР3ММ
может
дать
ущеСТlIенные
отклонеНЮI
от
реальности
.
ОДНИМ
из
способов
корреКТИРОНКl1
ситуации
и
получения
нмежных
з
ксперим
е
НТaJlЬНЫХ
nnrH10fpaMM
R
этой
Сl1туации
jlD.J1яеТ~~j
прим
е
нение
специальных
(роба
ст
ных
)
м
етодов
ДJ1H
их
расчета
.
Аы
юру
мо
деЛ
II
:
.н::t:перимеНТtlЛЬНОЙ
вариограммы
и
нахождению
зна'
lсtНIЙ
ее
парам
етр
в
может
пр
едш
ство
в
ать
преобрnзование,
которое
уменьшает
с.:м~щеllltе
ЭКС
ll
е
римен
таЛЫI
й
оариограммы
относительно
ее
мат
е
ма
ТИ'lе
'
КОI'О
о
Iщанин
для
дан
ной
простраНСТП~НtlОj.i
перемеl1НОЙ
н
даt-IНОМ
t
'
~UМСТР
И'l
еском
по
ле.
ОДНИМ
из
по
060В
такого
пре06ра
:
юnntlШI
ЯВJlнетсSI
Mt:TOA
"БОЛ
ЫIIОГО
складного
но
жи"
(jack-kllitc),
ко
то
рыН
был
11~
ДJlоже н
М.
Кенуйем
D
1956
Г.
с
целью
уменьшения
смещеННОСТI1
стат
и
тиче
'
КI1)(
оценок;
в
1958
г.
тот
метод
БЫ)1
развит
дж.тl
,
ЮК:И
ДJ1H
н\)с.:троеIlНJI
Д
uеритеЛЫIЫХ
Iflперв!VIOВ
таких
оценок
.
глаженная
оце
llка
:
:IК
'
I1
t:Р
lIмент
(
VIЫЮЙ
ljuриограмr.IЫ
,
полученшUl
м
етодом
CKJН
'
1101
'0
Н
ОЖrl,
име
ет
'ледующий
вид
:
y(tl)=Ky
(h)
-(
K-
1);
~1:
1y
;(
h),
(4.16)
где
y;(h) -
оцеllка
ваР
l10
грам",
ш
д
л
я
i
рnзбненин,
t= I,
...
KN,
по
uыб
орке
ЗШ
l1l
е
llИЙ
про
стра
llственной
перемеllНОЙ
X(t;), i
=:
1,
.... KN ,
где
К
-
чис
ло
ра
збне
JlI1Й
вь
борки,
N -
ЧIIСЛО
наблю
деН
IIЙ
D
каждом
разбвении
.
(10добраннан
модсль
y(h)
може
т
б
ыть проверена
на
достоверность
.
С
31'
Й
целью
методом
,
изложенным
8
главе
3
(см.
3.21),
с
исполь
зо
ванием
модели
y(h)
определяется
дисперсия
проб
заданной
ДJlI1НЫ
(1)
по
месторождеШ1Ю
.
Эта
расчетная
дисперсия
сравнивается
с
фаКТli1jескоЙ
.
Несущественное
отличие
между
ним
/
и
свидетельствует
о
надежности
взриогр
а
ммн
й
мод
е)
IИ
.
Ни
зка
я
надеЖ1l0
l'ь
и
н
едостато
чная
устойчивость
вuриограмм
обычно
свя
аны
с
о
'
клонениями
фактического
ра
с
пр
еде
ления
результатов
pa
~
НleДKH
ме<,,
:торожде
НI1Н
(
з
нач
с
ний
пространственно'Й
л
ереме
нной
в
l'eOMeTpl'I'ICt:KOM
nOJle)
0 '1'
нормального
.
СШ
I
такое
Оl'КJ1U
ll
е
IIИ
С
Ш.
'
t
с
т
~I
С
'
О
,
О
~j
С
ПОЛ
ЬЗУЮТ
ОДl
Ш
нз
трех
M
eToдoТl
:
11
'
КJ
lIO'l
e
llll
1
1:1
11
Сл
()
J
IlЮГО
Мllож
е
ТШ\
Il
eT
1tnll'IHbIx
(
'"
гр
'
М,
)
11.1-1"'
, )
:3
IНlчt:Нllii
,
J
lOгаРI
'
lфr.ШРОВ
3
11и
е
З
lf:lч
ен
иii
5

про(:траш;твrнной
переменной
или
примсн
е
llИС
neЦlHU1t>HblX
методов
расчета
З
КСl1еримеllЛlЛЬНЫХ
вариограмм
.
И~
них
наиболее
известен
метод,
преДJlО
же
нный
Н
.
~ресси
131,
который
р
е
ком
е
ндует
рассчитывать
варl10
раммы
110
формуле
y(h) =
[2~
r.Z,
IX(ti+h)-Х(ti)ltТ
/
(о.
457+~~
(4.17)
или,
в
случае
примененин меДlШННЫХ
оценок,
по
фuрмуле
2Y(fl)
:::
~e(lx(t+h)
-
X(t
)lt)T/(O.457+~~
(4.18)
Точки
Вilриограммного
облака
могут
быть
также рассчитаны
по
1
формуле
Ix(t+
h ) -
x(t)12.
(4
.
19)
Проверка
и
анализ
предлагаемого
подх
ода
ПОКiiЗали
его
эффективность
при
использовании
выборок
пространственных
переменных
с
э
кстремалЫIЫМИ
значениями.
За
счет
двойного
преобразования
(извлечен
ин
корнн
и
возведеНЮI
в
четвертую
степень)
можно
значительно
.
уменьшить
l1JIияние
этих
оценок
на
поведение
ЭКСllерilментальной
взриограммы
.
80И
методы
повышения
надежности
и
устойчивости
вариограмм
предлагают
также
М
.
Армстронг,
Р.Диамонд
(5},
ПДауд
16]
,
с.Чанг
I7J
,
Х
.
Омре
18),
М
.
Дагберт,
М.Давид
19)
)f
другие
исследователи.
Однако,
по
мнению
М
.
Армстронг
1101
,
использования
этих
приемов
В
большинстве
сл)"
laeB
удается
избежать
,
если
тщательно
подойти
к
анализу,
проверке
и
классификации
исходной
информации,
так
как
ГJlавные
причины
неустойчивого
поведения
вариограммы
связаны
с
некорректным
примен
..
и
е
м
результатов
разведки
месторожден~UI
и
неправильным
заданием
Н
'
'ШJlЬНЫХ
парамеТРО8
расчета
экспериментальных
вариограмм
.
4.3.6.
Проверка
выбранных
моделей
BapHorpaMM
KnK
было
отмечено
выше
I
надежность
геостати
тических
решений
зависит
от
устойчивости
моделей
экспеРИМСflтrU1ЬНЫХ
вариограмм,
которая,
D
свою
очередь,
завнсит
от
у
да
чного
выбора
модели
конкретной
BaplIorpaM~fbI
И
от
того,
насколько
принятые
параметры
модели
соответствуют
характеру
и
особенностям
I1ространстоенной
изменчивости
геологической
llеременноЙ
.
Единственное,
что
обычно
известно
о
месторождении
на
этом
этапе
-
это
содержания
в
пробах,
по
э
тому
наllЛУ"lшей
проверкой
будет
ВОСf1роизведение
этих
фактических
данных
опроБОВt\ния
,
используя
полученную
вариограммную
модель.
Решение
этой
проблемы
обеспечивается
перекрес1'НОЙ
I1ровеРК011
моде
J
IСЙ
варнограмм
[] 1 J.
Метод
перекр стной
про
верки
(cross-validariol1)
был
преДТlOжен
П
.
Дельфинером
в
1976
г
.
для
выбора
.
наилучшей
модели
конариационной
функции
при
определении
сосг
ава
э
кспертн
й
группы,
формируемой
с
целью
выработки
оцеНо
t
lНЫХ
заключений
и
прИJlЯТИЯ
управленческих
решеНIfЙ
.
Этот
метод
реализуется
следующими
процедураМ~1:
1)
выбором
модели
экспер
им
е
Н1альной
оариограММbl
прострав
ствен
ной
переменной
И
ПРИНflТllем
таких
ЗШt(lеЮIЙ
ее
111\
18метров,
которы
е
предстаВЛЯЮТСJl
по
дходящ
ими
;
8

2)
удалением
из
имеющейся
экспериментальвой
'
ВЬJборки
фактического
з
н
а
ч
е
ния
переменнойв
одной
и
з
опробованных
точек
гео~етричеекого
поля
11
оцсвкой
зна'lения
переменной
в
этой
TO'IKe
по
оставшейся
вы
борке
геостатистическим
способом
при
помощи
кригинга
с
выбрпнной
моделью
вариограммы
;
эти
расчеты
СОПРОВОЖД:1Ю
ТСН
опреде
J
l
ением
дисперсии
соответствующей
оценки
кригинга;
3)
повтор
ением
шага
(2)
для
всех
значений
выБОРЮI
и
вычислением
кuпдрптов
разностей
между
фаК
'
J,'Ическими
зна'Jениями
переменной
и
ее
геостатисти'IC~СКИМИ
оц
енк
ами
;
4)
нормированием
квадратов
ра
зностей
на
дисперсии
оценок
кригингав
соответствующих
точках
'
геометрического
поля.
и
вычислени
ем
сред
н
его
ЗН<l'lенин
и
стандартного
отклонения
нормированных
Кl:щдратов
разностей
по
всему
геометрическому
полю;
5)
nOBTOpeHl1eM
шагов
2-4
для
каждого
из
приннтых
значений
пар
аметров
выбранной
модели
вариограммы;
в
качеств
е
наилучшего
выбирается
такой
вариант
модели,
для
которого
среднее
значение
квадратов
разностей
ближе
других к
нулю,
Если
получ
енные
результаты
проверки
будут
преДСТ<lВЛЯТЬСЯ
неУДОВЛСТВОР"ТСJlЬНЫМИ,
то
выбира
тся
друган
модель,
про
верка
паР:1метров
которой
выполняется
описанным
способом
.
Рассмотрен
на
процедура
проиеРКII
параметров
модели
получила
название
процедур
пропуска
одного
наблюдения
,
Развитием
этой
процедуры
в
геостатистике
ЯWНlется
пр
едложенн
ый
несколько
р:1ньше
с.геЙсером
(1975)
метод
пов
торного
выборu
для
пр
едсказ:1НИН
.
Метод
.
ГеЙ
ера
усиливает
ВО
:
iМожности уroчнения
зна'
l
ений
п
ара
метров
моделей
вариограмм
благодаря
СИСТематически
повторяющему
с
Sl
части'lНОМУ
IIСПОЛЬЗОВtШИЮ
исходных
данных,
т
.
к.
в
нем
примеШI
тен
1Jазбl1еНl1е
ИСХОДIIOЙ
выборки
на
группы
з
начений
переменной
(и
ПрОI1УСК
одного
наблюдения
яuляетсл
частным
примером
рассматриваемuй
меТОДИКIt).
В
том
случае
при выборе
наt-шучших
параметров
мо
д
ли
впрнограммы
среднюю
меру
р(\схождения
м
ежд
у
фактичеСКIIМИ
ЗИП'
ениями
пространственной
пер
еме
нной
и
ее
оценками
,
птимизируемую
по
совокупности
параметров
модели
а.,
можно
представить
в
следующем
виде:
D N
,п
(а)
=
к
,-;
r.~
1
Е[
л{t,/П)
x'(t;
)(п)
(x(t)(~n),
rN-п)
,
т
(п),
а)
J,
(4.20)
где
'
х(д
=
[x(t
1)
, X(t2), .. " X(tN)]
выборка
значений
проетр:шствею-юй
переменной
объемом
N,
Т
-=
(t
1,
t
2,
....
, t
N)
-
век
т
ор
координа
т
то
ч
ек
наблюдения
этой
ныборки,
tj -
координата
i
наблюдения
,
К
-
число
разбиений
выборки
IШ
n
и
(N-n)
Н:1блюдений,
Е
~Iepa
расхождения
между
истинными
зна
чениями
и
их
оценками,
нолучеНJ[ЫМИ
по
(N
-
п)
наБJlюдениям,
).(t;) -
оц
е
нка
з
начения
llе~сменной
в
пропущ
ен
ной
точке
(;
.
Оптимальность
понимаетс}!
в
СМЫl,;ле
шаг
а
(5)
ВЫl
,
uеОГlи
сашюй
процедуры
пеv
КреСТНОЙ
проверки
.
87

ОпреДСJlпемые
перекрестной
llРОВСРКОЙ
п
а
раметры
моделей
ЬаРlюграмм
хар:\Ктери
з
уются
огр:ши'~енно
тыо
и
У~
JЮВ
t-IOСТЬЮ,
которые
обусловлены
отсугствием
однознаЧIIЫХ
ответов
11:1
СJJсдующие
вопросы:
а)
какова
подхощшl.:lЯ
м
ер
[\
расхождеll~Ш
фаКТИ'lеских
и
рассчитанных
значений
npocTpall
твеНIЮЙ
II
с
ремеююй?
б)
как
определить
множество
ра
:
UНlЧIIЫХ
I1нтеРIIОЛИРУЮЩИХ
ФУНКЦИЙ
ДJШ
зманной
схемы
ра
зб исtlИН
исходной
uыБОРКI1
на
группы
наблюдений?
В)
как
выбрать
схему
разбиения
ПРI1
ЗЩЩНIIЫХ
интерполирующей
ФУНКЦJlII
и
наборе
д[\нных?
г)
как
свя
зат
ь
меру
расхuждеюш
с
оценкой
при
условии
совместнorо
выбора
интерполирующей
ФУ'IКЦИИ
и
схемы
разбиения?
Наиболее
обоснованно
может
быть
решен
вопрос
о
выборе
интеРПОЛllрующей функции.
Если
D
ка'Jсстпе
меры
расхождения
выбрана
разность
e=k(t;)-x(t;)
,
то
КРИГl1НГ
будет
наилучшей
линейной
интерполяцией,
обеСПС'lиваюu(
е
й
II
сс
мещснность
оценок
с
Мltнимальной
дисперсией.
При
решею'IИ
OCTi1JlbIlbIX
трех
вопросов
приходится
руководствоваться
такими
соображениями,
как
удобство
и
простотавычltслений,
но
следует
отдавать
себе
OT'ICT
в
том,
что
при
этом
отнюдь
не
всегда
достигаетсн
оп
т
имальность
в
математическом
смысле.
Из
сказанного
следует,
что
модель
вариограммы,
признаннаf(
луt{шей
с
помощью
метода
п
е
рекрестной
проверки,
ЯВJJяется
таковой
лишь
для
выбранной
меры
расхождения,
схемы
разбиения,
интерполltрующей
ф
у
нкции
и
числа
конкурирующих
моделей
,
и для
данного
РJI)Щ
наблюдений.
И
з
менение
даже
одного
из
этих
условий
может
привести
к
иной
лучшей
модели.
Таким
образом
,
метод
п
е
рекрестной
проверки
нельзя
рассматривать
как
метод
доказательства
или
как
критерий
проверки
стаТИ~Тl1ческих
гипотез,
в
частности
,
о
м
одел
11
и
параметрах
вариограмм
.
Его
следует
воспринимать
и
использовать
как
исследовательский
метод
анализа
данных,
дающий
возможность
многократно
ИЗУ'JaТЬ
и
переформулировать
модель
,
добиваясь
наи.try'fшего
соответствия
модели
и
имеЮЩИХСf(
данных
.
В
системе
ДАТАМАЙН
имеетС11
процесс
РТКЗDА
,
который
выполняет
перекрестную
проверку.
В
реэультате
перекрестной
проверк.и
Вы
получите
для
каждой
проверн
мой
модели
дополнительные
переменные
в
имеющийся
массив
исходных
данных:
-
оценку
содержаюНl
в
пробе,
-дисперсию
кригинга
для
этой
оценки
,
-ЧИСJlО
проб,
по
которым
сделана
эта
оцеllка,
а т:н
~
же
диаграмму
разброса
ДНЯ
фактических
и
оцененных
величин
содержаний.
Теперь
с
помощью
корреляционного
анализа
возможно
оценить
н:.
сколько
далеко
тоtlКИ
полученной
диаграммы
р[\ссеШIИЯ
удалены
от
линии
Х
=
У,
т.е.
вычислить
коэффициент
корреJUЩН~1
фактиче
с
ких
и
(
.
щененных
величин
.
Та
модель
,
которая
ДflС
б()лее
высокий
коэффициен
,
будет
предпоч
т
ительней
Дll
Я
ИСПОЛЬЗОВ3I11Ш
,
чем
дРугие.
Не
надо,
однако,
уповать
н
а
то
,
что
данный
метод
11
100%
случаев
будет
ПU)i.сказывать
В
м
праВИJ1ыю
е
решение.
В
практике
геостатистики
и
в
С1'
но
достаточ
но
трудных
ситуаций,
когд
в
с
е
Н
СПЫТЫFшем
ые
модели
да)
т
при
пр
оверке
одинаковые
ре
ультаты.
88
• 4.4.
При
меры
4.4.1.
Создаlше
ваРИОI
'
раммной
модели
ДJUI
участка
мес
торождении
.
апатит-"
Для
этой
работы
были
использованы
результаты
эксплуатационной
ра
зве
дки
(керноное
бурение
скважин
и
штуфное
опробование
подземных
ИЫР1-\боток)
участка
Кукисвумчоррского
апатито-нефелинового
месторождения
в
Мурманской
области.
Месторождение
отрnбатывuется
в
основном
подземным
.
способом
и
предстаВJlнет
собой
пологопадающую
(под
'
углом
25-30
град)
на
СВ
залежь
МОЩIJOСТЫО
50 - 200
М
.
ЭксперимеН1i1льные
данные
по
блоку
13/15
горизонта
+252
м
предстаВЛЯllИ
собой
информацию
о
1015
пробах,
их
УСЛОВНЫХ
координатах
и
результатах
опробования
на
содержание
Р205
и
А1203
.
Эти
массивы
были
внедены
в
программу
Датамайн
с
соответствующим
переходом
к
абсолютной
географической
системе
'
координат.
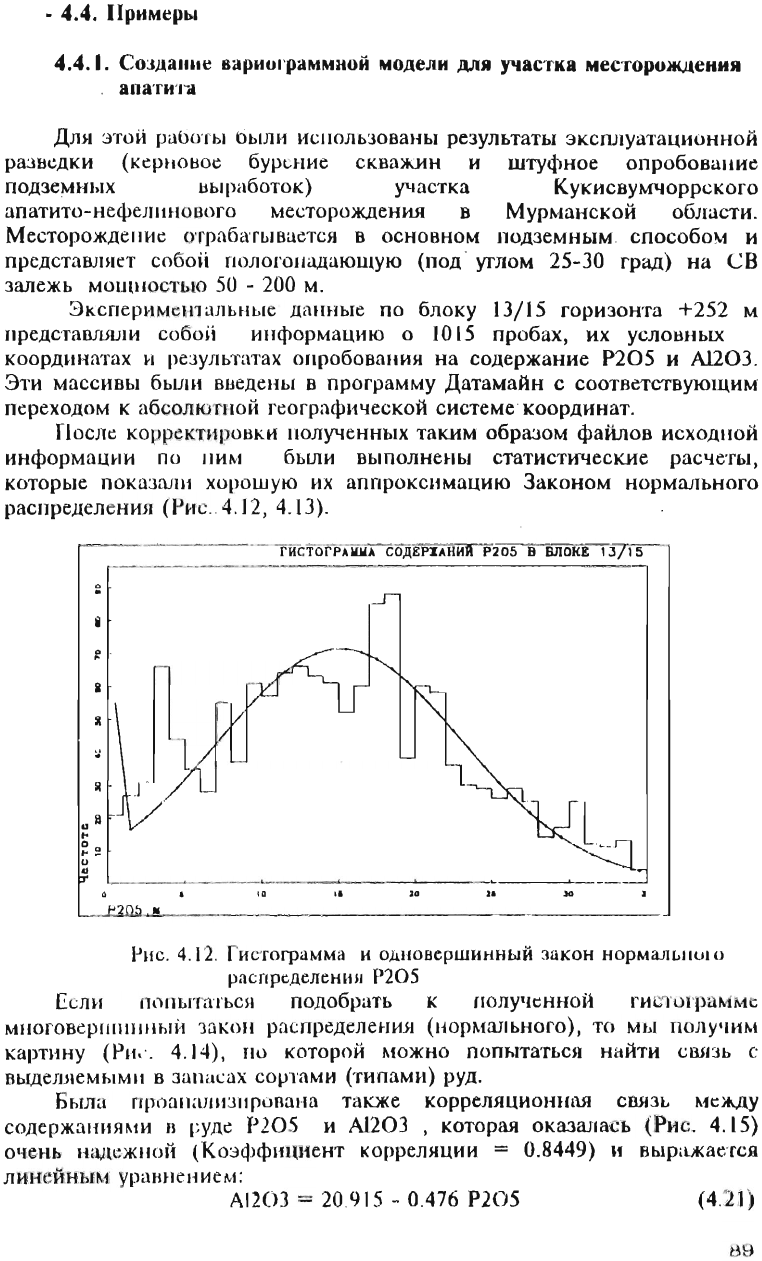
После
корректировки
полученных
таким
образом
файлов
исходной
информации
по
ним
бьши
выполнены
статистические
расчеты,
которые
пока
зали
хорошую
их
аппроксимацию
Законом
нормального
распредел
ени
я
(P",c
..
4.
12
, 4.13).
о
.
I
,,11
..
0 0
..
-
u
u
'-
ГИ-СТОГРА
IOiА
СОДЕРJ:АНИ
Р205
В
БЛОКЕ
13
15
,
О
'1
••
..
..
Р205
•
l'IfC. 4.12.
и(
:
то
грамма
И
ОДllОВСрШИННЫЙ
закон
нормальногu
Рn
СПрtЩСЛС
НИjJ
Р205
Е<.;ли
11'-
l1ытатьсSl
подобрать
к
полученной
ГИСl'(Я
'
раммс
многов
е
РLШlllllыi1
з
акон
р
аспределе
ния
(нормального),
то
мы
полу'lИМ
картину
(Ри
. 4.14),
110
которой
можно
попытаться
найти
С
WIЗЬ
с
выделяемыми
в
за
п
асах
сортами
(типами)
руд.
Была
ПРО(lIlШIl1ЗI1РОО:lна
также
корреляционная
сnяз!.
Мt:ЖДУ
содеРЖ:lНИЯМИ
пруде
Р205
и
Al20
,которая
оказапась
(Ри
с
.
4.15)
очень
н
адеж
ной
(КоЭффициент
корреляции
= 0.8449)
и
выра.жается
линейным
уравн
е
нием
:
А
I20З
=
20
.
15
~
0.476
Р205
(4.
2J)
