Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

680 14 Electromagnetism II

Thus ∇×(∇×F) =−6x

i +6xz

k (1)

−∇

F +∇(∇·F) =−(6x

z + 2z

)

i +2z

i +6xz

=−6x

i +6xz

k (4)

Comparing (1) and (4), the identity

∇×(∇×E) =−∇

E +∇(∇·E) is veriﬁed.

14.70 The electric ﬁeld of the cable is radial and is given by

E = E

r ln(b/a)

(1)

where a and b are the radii of the inner and outer cable. The corresponding

magnetic intensity is tangential and is given by

H = H

2πr

(2)

As the angle between E and H is 90

◦

, the Poynting vector

E × H

= EH (3)

So that S = S

2πr

ln(b/a)

(4)

and the direction of S is that of the current in the positive conductor.

The power ﬂow is conﬁned to the space between the conductors and for any

plane perpendicular to the axis of the conductor

P =



2πrdr =



ln(b/a)

(5)

where we have substituted S

from (4).

But



= ln(b/a) (6)

∴ P = VI (7)

This is the entire power transmitted by the cable. It follows that the Poynting

theorem indicates that the entire ﬂow of energy resides in the space between

the conductors.

14.3 Solutions 681

If the resistance of the cable cannot be neglected then V is no longer constant.

An axial component of E is necessary to maintain the ﬂow of current to

compensate for the Ohmic energy loss.

14.71 The current density in the wire is (I/πa

)ˆe

. Therefore the electric ﬁeld in

the wire, including on the surface of the wire, will be (I/πa

)ˆe

The magnetic ﬁeld intensity by Ampere’s theorem is (I/2πa

)ˆe

The Poynting vector at the s urface is given by

S = E ×H =



πa

ˆe





2πa

ˆe



=−

2π

ˆe

(1)

Now Poynting’s theorem is

−



(E × H) · ds =

∂

∂t



dV +

∂

∂t



dV +



E · J dV (2)

Since the ﬁelds are constant in time, the ﬁrst two terms on the right of (2)

which contain time derivative ∂/∂t vanish. The power dissipated in the wire

is then

P =



E ·JdV =−



(E ×H) · ds =−

2π

(2πaL) =

πσ

= I

14.72

Given B =−

∇ × J (1)

Use the vector identity

∇ × (∇ × B) =−∇

B +∇(∇ · B) (2)

Use Maxwell’s equations

∇ · B = 0(3)

∇ ×

= J +ε

∂E

∂t

(4)

Here

∂D

∂t

= ε

∂E

∂t

= 0(5)

so that (4) becomes

∇ × B = μ

J (6)

Using (3) and (6) in (2)

682 14 Electromagnetism II

∇ × J =−∇

B (7)

Using (1) in (7)

∇

B =

14.73 High-frequency resistance



ωμ

2σ

(1)

Direct current resistance per metre

R =

σ A

σπr

(2)

Further the skin thickness

δ =



μσ ω

(3)

For metals assume μ = μ

. Combining (1), (2) and (3)

πr



π(10

−3

)

6.6 × 10

−5



4π ×10

−7

= 3.77 ×10

−5

14.74 When a charge q moves in a magnetic ﬁeld, it experiences a magnetic force

= qv × B (1)

When an electric conductor is physically moved across a magnetic ﬁeld, the

free electrons in the conductor will experience a force on them in the direc-

tion of the force. The ﬂow of electrons implies the existence of a potential

difference between the ends of the conductor. The situation is the same as if

an electric ﬁeld had been set up in the conductor which is expressed by the

relation

= F

/q = v × B V/m(2)

Equation (2) implies that every moving magnetic ﬁeld is accompanied by an

electric ﬁeld.

From (2) and the deﬁnition of the emf ξ of a source, the instant emf of the

source is

14.3 Solutions 683

ξ =



· dl =



v × B ·dl V(3)

This is the general expression for motional emf. Now Faraday’s law states

that



· dl =−

dφ

(4)

This equation states that every time-changing magnetic ﬁeld has an electric

ﬁeld associated with it. Now the total ﬂux through the surface is

φ =



B ·ˆnds (5)

Therefore

dφ



B ·ˆn ds (6)

If the source and only the induction are changing, d/dt outside the integral

may be replaced by ∂/∂t inside the integral. The expression becomes

dφ



∂B

∂t

·ˆn ds (7)

Combining (7) with (4)



· dl =−



∂B

∂t

·ˆn ds (8)

Transforming the line integral in (8) into surface integral by the use of

Stokes’ theorem



E · dl =−



ˆn · (∇ × E) ds (9)

Combining (8) and (9)



n · (∇ × E) ds =−



ˆn ·

∂B

∂t

ds (10)

Since this expression is true for any surface, the two integrals in (10) can be

equated to yield

∇ × E =−

∂B

∂t

(11)

This is known as Faraday’s law in point form or differential form.

684 14 Electromagnetism II

14.75 Ampere’s law is expressed by



B · dl = μ

i (1)

where B is known as magnetic induction or magnetic ﬁeld. Its unit is weber

per metre square or tesla. If magnetic materials are placed in the ﬁeld of

induction, the elementary magnetic dipoles, permanent or induced, will set

up its own ﬁeld that will modify the original ﬁeld. A large value of B in an

iron core is explained by a subsidiary vector, the magnetization M which is

the magnetic moment per unit volume of the core material. A hypothetical

current i

is introduced and Ampere’s law, (1), is modiﬁed accordingly:



B · dl = μ

(i + i

) (2)

Writing



B · dl = μ

i +μ



M · dl (3)

we ﬁnd





B − μ



· dl = i (4)



H · dl = i (5)

where H =

B −μ

(6)

is known as the magnetic ﬁeld strength.

∴ B = μ

(H + M) (7)

The unit of H is henry/metre.

(a) For paramagnetic material B is directly proportional to H, the relation

being B = k

H, where k

is the permeability of the magnetic

medium, which is a constant for a given temperature and density of the

material.

(b) In ferromagnetic materials the relationship between B and H is far from

linear. The B–H curve is known as the familiar hysteresis curve. k

is a

function not only of the value of H but also because of hysteresis and is

a function of the magnetic and thermal history of the specimen.

14.76 Consider Maxwell’s equations

∇ · E = ρ/ε (1)

14.3 Solutions 685

and ∇ × H = J +

∂D

∂t

(2)

Deﬁne a new electric potential function φ(r, t) such that

E =−∇φ −

∂A

∂t

(3)

The reason for redeﬁning the scalar potential in this fashion is that (3) is

consistent with Faraday’s law, ∇ × E =−

(

∂B/∂t

)

, as can be veriﬁed by

substitution. On the other hand the electrostatic deﬁnition, E =−∇V is

inconsistent with Faraday’s law and therefore cannot be used in electrody-

namics. However, the relation B = ∇ × A, continues to be correct. Substi-

tuting (3) in (1), we obtain

∇

φ +

∂

∂t

(

∇ · A

)

=−

(4)

Substituting B = ∇ × A in (2), we get

∇

A − ∇(∇ · A) =−μJ −με

∂E

∂t

(5)

It is convenient to choose a Lorentz gauge given by

∇ · A =−

∂ϕ

∂t

(Lorentz condition) (6)

With the use of (6), (4) and (5) are simpliﬁed to

∇

ϕ −

∂

∂t

=−

(7)

∇

A −

∂

∂t

=−μJ (8)

14.77

∇ × E =−

∂B

∂t

(Faraday’s law) (1)

Writing the curl in rectangular form gives

∂ E

∂z

=−

∂ B

∂t

Integrating in time and choosing the constant of integration as zero, we

obtain

f (z − vt) (2)

686 14 Electromagnetism II

Notice that the variation of B is exactly the same as the variation of E, except

that E

and B

are at right angles to each other and perpendicular to the

direction of propagation. From (2) and the relation H

= B

/μ

we ﬁnd

f (x −vt) (3)

so that E

= μ

v H

(4)

Using the relation v =

√

1/μ

, we can write (4) in the form

= Z

with Z



= 376.6 .

14.78

(a) E(z, t) = E

[ˆx sin(kz − ωt) +ˆy cos(kz − ωt)]. This is a plane polar-

ized wave polarized in the xy-plane and propagating in the positive

z-direction.

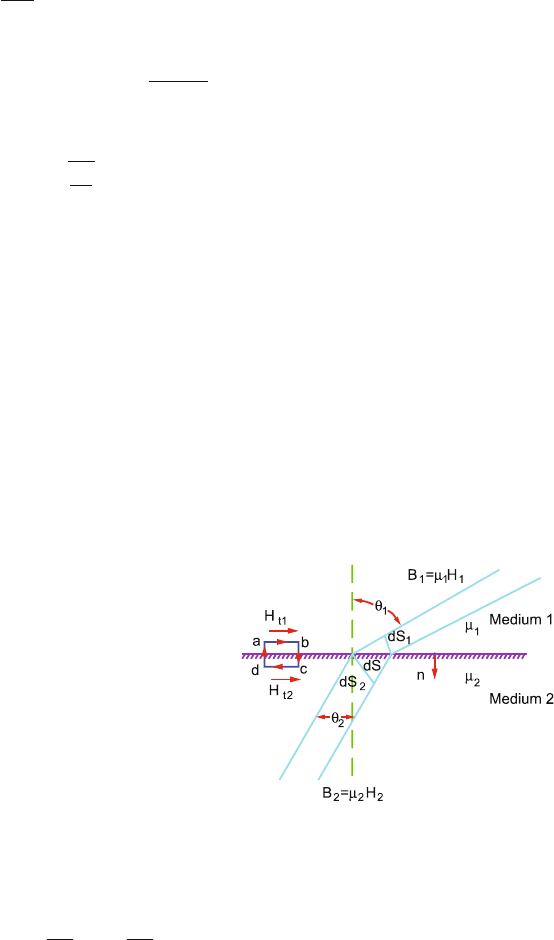
(b) The magnetic lines will suffer refraction in passing from one magnetic

medium to another.

(i) The continuity of B lines is ﬁrst speciﬁed as a necessary condi-

tion. Figure 14.8 shows a bundle of B lines in passing through the

interface between two magnetic media characterized by μ

and μ

(ii) Since div B = 0, it is required that the magnetic ﬂux associated

with the ﬂux lines be constant in passing through the interface.

φ = B

= B

Fig. 14.8 The refraction of

magnetic lines

where ds

and ds

are the cross-section of the ﬂux lines in medium

1 and 2, respectively. Dividing by ds, the corresponding area on the

interface, we get

= B

14.3 Solutions 687

which from Fig. 14.8 may be written as

cos θ

= B

cos θ

(1)

which may be written as

·ˆn = B

·ˆn

which shows that the normal component of the B vector is the same

on both sides of the boundary.

(iii) Next we apply Ampere’s circuital law to the path across the inter-

face, Fig. 14.8. Assuming that no current exists in the interface, for

the path considered



H · dl = 0

Breaking the integral into individual parts of the path



H · dl =



H · dl +



H · dl +



H · dl +



H · dl = 0

In the limit the path shrinks approaching the interface



H · dl =



H · dl = 0

∴



H · dl +



H · dl = 0

Thus H

= H

i.e. H

×ˆn = H

×ˆn (2)

This implies that the tangential component of the H vector is the

same on both sides of the boundary.

sin θ

cos θ

sin θ

cos θ

∴

tan θ

∴

tan θ

(law of refraction)

688 14 Electromagnetism II

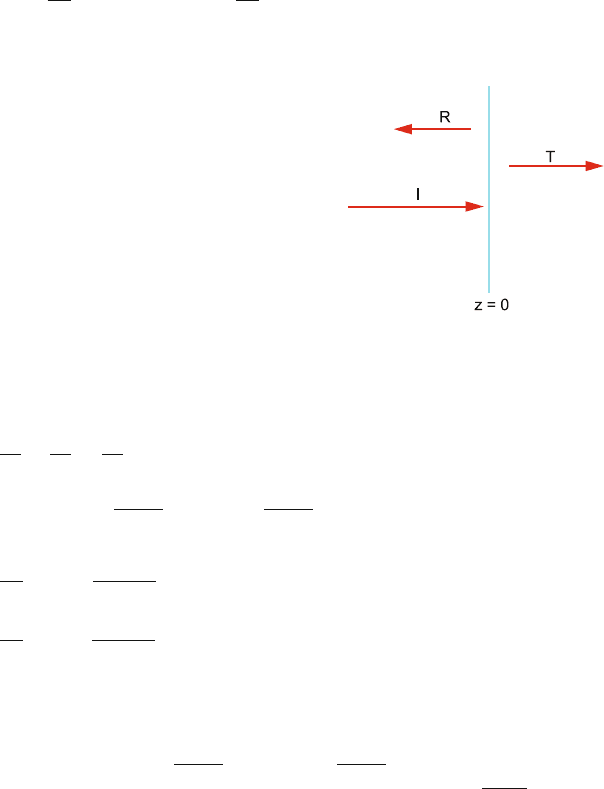
14.79 Consider a plane wave normally incident on a dielectric discontinuity, as in

Fig. 14.9. In the region z < 0, ε = ε

, and for z > 0, ε = ε

. The boundary

condition on E is that its tangential component is continuous, the boundary

condition on H is that its tangential component is also continuous.

(z = 0) + E

(z = 0) = E

(z = 0) (1)

(z = 0) + H

(z = 0) = H

(z = 0)

Letting E

= E

−jkz

, E

= E

jkz

, E

= E

−jkz

and H

=−

−jkz

(2)

Fig. 14.9 Reﬂection of plane

waves normally incident on

the interface between two

dielectrics

and substituting in (1), we obtain

+ E

= E

(3)

−

(4)

where η

√

/ε

and η

√

/ε

. Solving, we ﬁnd

= ρ =

− η

+ η

(5)

= τ =

2η

+ η

(6)

Note the minus sign in the last relation for H

in (2) arises because the Poynt-

ing vector S = E × H must be in the direction of propagation (right-hand

rule).

Substituting η

√

/ε

and η

√

/ε

in (5) and (6) and setting

= μ

for non-magnetic substances, and putting

√

/ε

= n

for the refractive index, we obtain

14.3 Solutions 689

R = ρ

(

− n

)

(

+ n

)

(7)

T = τ



+ n



+ n

)

(8)

Adding (7) and (8) it follows that R +T = 1. This is simply the consequence

of conservation of energy.

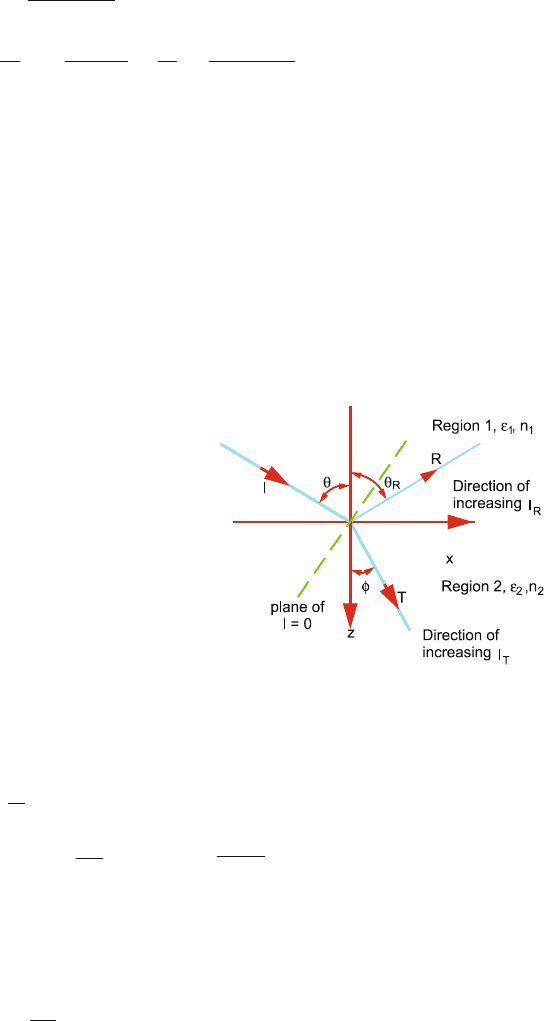
14.80 Refer to Fig. 14.10. Consider a plane perpendicular to the propagation direc-

tion through the origin. Let the distance from this plane measured in the

direction of propagation be called l. If the coordinates of a point are x, z,

then

= x sin θ + z cos θ (1)

Fig. 14.10 Reﬂection and

Refraction of electromagnetic

wave

As the electric ﬁeld is in the plane of incidence, for the incident wave

= E

(cos θ e

− sin e

)

−jk

(2)

where k

= ω

√

νε

and η

√

/ε

are the values of the propagation

constant and characteristic impedance in region 1.

For the reﬂected wave l

= x sin θ



− z cos θ



(3)

⎧

⎨

⎩

= E

−jk

(cos θ

+ sin θ

)

=−

−jk

(4)