Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

690 14 Electromagnetism II
For the transmitted wave the relations are
l
T
= x sin φ + z cos φ (5)
⎧
⎨
⎩
E
T
= E
T
e
−jk
T
l
T
(cos φ e
x
− sin φe
z
)
H
T
=
E
T
η
2
e
−jk
T
l
T
e
y
(6)
The boundary conditions at z = 0 require that the tangential E that is E
x
and tangential H
y
be continuous. Setting E
x
(z = 0) in region 1 equal to
E
x
(z = 0) in region 2,
E
0
cos θ e
−jk
I
x sin θ
+ E
R
cos θ
R
e
−jk
I
x sin θ
R
= E
T
cos φe
−jk
T
x sin φ
(7)
If this equation is to hold for all values of x then
k
I
sin θ = k
I
sin θ
R
= k
T
sin φ (8)
It follows that θ
R
= θ, that is, the angle of incidence is equal to angle of
reflection as in a plane mirror.
Further
sin φ
sin θ
=
k
I
k
T
=
√
ε
1
√
ε
2
=
n
1
n
2
(9)
where n is the index of refraction of the material. Equation (9) then gives
Snell’s law (n
1
sin θ = n
2
sin φ) which holds irrespective of the nature of
polarization. Using (9) in (7) and cancelling the exponential terms we have
E
0
cos θ + E
R
cos θ = E
T
cos φ (10)
Using (8), the boundary conditions on H
y
yield
E
0
η
1
−
E
R
η
1
=
E
T
η
2
(11)
Solving (10) and (11) we get
E
R
E
0
=
η
2
cos φ − η
1
cos θ
η
2
cos φ + η
1
cos θ
(12)
E
T
E
0
=
2η
2
cos θ
η
2
cos φ + η
1
cos θ
. (13)
Substituting η
1
=
√
μ
1
/ε
1
,η
2
=
√
μ
2
/ε
2
,μ
1
= μ
2
= μ
0
for non-
magnetic dielectric and using (9) in (12), we obtain
14.3 Solutions 691
R =
E
1
E
0
2
=
n
2
cos θ − n
1
cos φ
n
2
cos θ + n
1
cos φ
2
14.81
(a)
Reflectance R = 0ifn
2
cos θ − n
1
cos φ = 0(1)
Given tan θ =
n
2
n
1
(Brewster’s law of polarization) (2)
sin θ
sin φ
=
n
2
n
1
(Snell’s law of refraction) (3)
Combining (2) and (3), we have (Fig. 14.11)
sin φ = cos θ (4)
or φ = 90
◦
− θ (5)
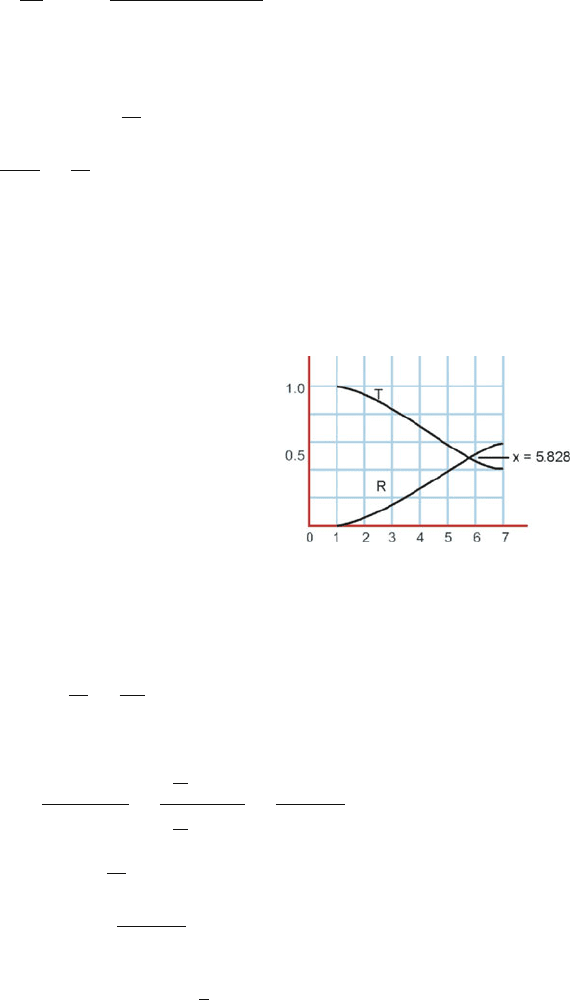
Fig. 14.11 R and T against n
1
/n
2
Eliminating n
2
between (1) and (2)
n
2
cos θ − n
1
cos φ = n
1
(sin θ − cos φ) = n
1
(sin θ − sin θ) = 0 where
we have used (5).
(b)
tan θ =
n
2
n
1
=
1.5
1
= 1.5
∴ θ = 56.31
◦
14.82
(a)
R =
(
n
1
− n
2
)
2
(
n
1
+ n
2
)
2
=
n
1
n
2
− 1
2
n
1
n
2
+ 1
2
=
(
x − 1
)
2
(
x + 1
)
2
(1)
where x =
n
1
n
2
T = 1 − R =
4x
(x + 1)
2
(2)
(b) Setting R = T yields the quadratic equation x
2
− 6x + 1 = 0, whose
solution is x = 3 + 2
√
2 or 5.828. Thus for n
1
/n
2
= 5.828, we get
R = T = 0.5.
692 14 Electromagnetism II
14.83 Using Maxwell’s equations
∇ · E = 0(1)
∇ · B = 0(2)
∇ × E =−
∂ B
∂t
(3)
(a)
E = E
0
e
i(ωt−k.r+φ)
(4)
B = B
0
e
i(ωt−k.r+φ)
(5)
Let the wave be propagated in the z-direction. Then
∇ · E =−i k · E = 0
and ∇ · B =−i k · B = 0
This shows that both E and B are perpendicular to k, which is the direc-
tion of propagation. Therefore both E and B are transverse oscillations.
(b) B and E are in phase
(c) Using (3)
∇ × E =−i k × E =−iω B
∴ B =
k × E
ω
=
1
c
k × E
k
∴ B =
1
c
ˆ
s × E (6)
where ˆs = k/k is a unit vector in the direction of propagation. The three
vectors E, B and k form a right-handed rectangular coordinate system.
From (6) we obtain B = E/c.
14.84
E =
σ
2ε
r
ε
0
∴ σ = 2ε
0
ε
r
E = 2 × 8.85 ×10
−12
× 6 × 2 × 10
3
= 2.124 ×10
−7
C/m
2
14.3.3 Phase Velocity and Group Velocity
14.85 Using the result of prob. 14.93
1
V
g
−
1
V
p
=
V
p
− V
g
V
g
V
p
=
V
p
− V
g
c
2
−=
ω
c
dn
dω

14.3 Solutions 693
∴
V
p
− V
g
V
p
=
ωc
V
P
dn
dω
(1)
But ω = 2πν = 2πc/λ (2)
V
p
= c/n (3)
dn
dω
=
dn
dλ
dλ
dω
=−
λ
2
2πc
dn
dλ
(4)
Substituting (2), (3) and (4) in (1)
V
p
− V
g
V
p
=−nλ
dn
dλ
(5)
n
1
− 1
2.786 ×10
−4
2.781 ×10
−4
n
2
− 1
2.781 ×10
−4
2.777 ×10
−4
n =
n
1
+n
2
2
1 +2.784 ×10
−4
1 +2.779 ×10
−4
n
5 ×10
−7
4 ×10
−7
λ
1
(A)
4800
5000
λ
2
(A)
5000
5200
λ =
λ
1
+λ
2
2
4900 A
5100 A
λ = λ
1
− λ
2
−200 A
−200 A
Using formula (5), the first set of data gives (V
p
− V
g
)/V
p
= 1.22 × 10
−5
and the second set 1.02 × 10
−5
.
14.86 ω = ak
2
(a) v
p
=
ω
k
= ak
(b) v
g
=
dω
dk
= 2ak = 2v
p
14.87
(a)
v
p
=
1
√
εμ
(1)
(b) n =
√
ε
r
ε
r
= n
2
= 1 −
D
2
ω
2
∴ n =
1 −
D
2
ω
2
(2)
υ
p
=
c
n
=
c
1 −
D
2
ω
2
(3)
Squaring (3) and re-arranging
ω
2
= D
2
+
ω
2
c
2
v
2
p
= D
2
+ k
2
c
2
(4)
∴ v
p
= ω/k
694 14 Electromagnetism II
(c) Differentiating with D with c constant, ω
dω
dk
= c
2
k
∴ v
g
=
dω
dk
=
c
2
k
ω
=
c
2
v
p
= c
1 −
D
2
ω
2
∴ v
p
v
g
= c
2
(5)
(d) Substituting D = 1.2 × 10
11
/s, ω = 2π × 20 × 10
9
Hz and c = 3 ×
10
8
m/s in (3), we find v
p
= 1.016 ×10
9
m/s
Substituting υ
p
= 1.016×10
9
m/s in (5) we find v
g
= 8.858×10
7
m/s.
It is observed that while v
p
> c, v
g
< c.
14.88
V
g
=
dω
dk
(1)
ω = vk (2)
∴ V
g
=
d
dk
(vk) = v + k
dv
dk
(3)
14.89
V
g
= v +k
dv
dk
(by prob. 14.88)(1)
V = c/n (2)
Substituting (2) in (1)
V
g
= c/n + ck
d
dk
1
n
=
c
n
−
ck
n
2
dn
dk
(3)
Now
dn
dk
=
dn
dλ
dλ
dk
=
dn
dλ
d
dk
2π
k
=−
2π
k
2
dn
dλ
(4)
Using (4) in (3)
V
g
=
c
n
+
λc
n
2
dn
dλ
14.90
v ∝
1
λ
(by problem)
∴ v = Ak (where A = constant)
v
g
= v +k
dv
dk
= Ak + k
d
dk
(Ak ) = Ak + Ak = 2Ak = 2v
14.91
v
g
= v +k
dv
dk
= v +k
dv
dω
dω
dk
= v +kv
g
dv
dω
(1)

14.3 Solutions 695
Now v = c/n (2)
∴
dv
dω
=
dv
dn
dn
dω
=−
c
n
2
dn
dω
(3)
Substituting (2) and (3) in (1) and using ω = kv and rearranging we get
v
g
=
c
n + ω(dn/dω)
14.92
V
g
=
distance
time
=
50
1 × 10
−6
= 5 ×10
7
m/s
V
g
= c
1 − (λ/2a)
2
∴ 5 ×10
7
= 3 ×10
8
1 − (λ/5)
2
Solving for λ, we find the free-space wavelength λ = 4.93 cm.
V
p
=
c
2
V
g
=
(3 × 10
8
)
2
5 × 10
7
= 1.8 ×10
9
m/s
14.93
V
g
= dω/dk (1)
Rewriting (1), 1/V
g
= dk/dω
∴
1
V
g
=
d
dω
ω
V
p
=
1
V
p
−
ω
V
2
p
dV
p
dω
(2)
Substituting V
p
= c/n in (2)
1
V
g
=
1
V
p
−
ωn
2
c
c
2
−
1
n
2
dn
dω
=
1
V
p
+
ω
c
dn
dω
(3)
14.94
V
g
=
∂ω
∂k
∴
1
V
g
=
∂k
∂ω
=
∂
(
2π/λ
)
∂(2πν)
=
∂
(
1/λ
)
∂ν
But n =
c
v
p
=
c
νλ
→
1
λ
=
nν
c
∴ V
g
=
∂ν
∂
1
λ
=
∂ν
∂
(
nν/c
)
=
c∂ν
∂(n ν)

696 14 Electromagnetism II
14.95
v
g
=
dω
dk
=
d(ω
¯
h)
d(k
¯
h)
=
dE
dp
=
d
p
2
/2m
dp
=
1
2m
dp
2
dp
=
2p
2m
=
mv
m
= v
14.96 By prob. (14.85)
V
p
− V
g
V
p
=−nλ
dn
dλ
(1)
where V
p
=
c
n
(2)
Re-arranging (1) with the aid of (2) and writing μ for n we find
V
g
= c
1
μ
+ λ
d μ
d λ
(3)
μ = 1.420 +
3.60 × 10
−14
λ
2
(by problem) (4)
Substituting λ = 500 nm = 5 × 10
−7
min(4)
μ = 1.564 (5)
Differentiating μ with respect to λ in (4)
dμ
dλ
=−
7.2 × 10
−14
λ
3
or λ
dμ
dλ
=−
7.2 × 10
−14
λ
2
=−0.288 (6)
Substituting (5) and (6) in (3), we find V
g
= 0.35 c.
14.3.4 Waveguides
14.97
(a) Assuming the dominant mode, for a = 2.5 cm, and b = 2.5cm,forthe
rectangular waveguide, and c = 3×10
8
m/s, the velocity of electromag-
netic waves in free space, the phase velocity is given by
V
p
=
c
1 − (λ/2a)
2
=
3 × 10
8
1 − (4/5)
2
= 5 ×10
8
m/s
(b) V
g
= c
1 − (λ/2a)
2
= 3 ×10
8
1 − (4/5)
2
= 1.8 ×10
8
m/s
(c) λ
g
=
λ
1 − (λ/2a)
2
=
4
1 − (4/5)
2
= 6.67 cm

14.3 Solutions 697
14.98
λ
g
=
λ
1 − (λ/2a)
2
(1)
λ
g
= 3λ (by problem) (2)
Combining (1) and (2) and solving for λ with a = 3 cm we find the free-
space wavelength λ = 4
√
2cm.
14.99
(a) λ
g
=
λ
1 −
(
λ/2a
)
2
=
8
1 −
(
8/10
)
2
= 13.33 cm
(b) The cut-off wavelength λ
c
= 2a = 2 ×5 = 10 cm.
14.100 N =
8πν
2
dνV
c
3
=
8πdλ · V
λ
4
Mean λ = 5500Å = 5.5 × 10
−7
cm
dλ = (6000 − 5000)Å = 10
−7
cm
V = (0.5)
3
cm
3
N =
8π × 10
−7
× (0.5)
3
(5.5 × 10
−7
)
4
= 3.43 ×10
18
14.101 The cut-off frequency of the TM
mn
or TE
mn
mode is
ω
mn
= c
πm
a
2
+
πn
b
2
1/2
The lowest value we can have for ν
mn
is for the choice m = 1, a = 15 and
n = 0, that is, for TM
10
wave.
∴ ν
10
=
c
2
×
1
15
=
3 × 10
8
30
= 10
7
Hz = 10
4
kHz
This is much above the range of AM waves (530–1600 kHz). Hence AM
waves cannot propagate in the tunnel.
14.102 The cut-off frequency will be least for TE
10
waves. Of course TM
10
waves
do not exist.
ν
10
=
c
2π
π
a
=
c
2a
=
3 × 10
8
2 × 0.05
= 3 ×10
9
Hz = 3 GHz
Note that we take the higher dimension (5 cm) for the lower value of cut-off
frequency.

698 14 Electromagnetism II
14.103 The relation between ω and k in a rectangular waveguide is
k
2
=
ω
2
c
2
−
mπ
a
2
−
nπ
b
2
(1)
For TE
01
waves m = 0, n = 1, a = 1 cm and b = 2 cm. Equation (1) is
then reduced to
k
2
=
ω
2
c
2
−
π
0.02
2
(2)
The phase velocity is given by
v
p
=
ω
k
(3)
The group velocity ν
g
is given by
v
g
=
dω
dk
(4)
v
g
=
dω
dk
=
kc
2
ω
=
c
2
v
p
or v
p
v
g
= c
2
(5)
The cut-off frequency is given by
ω
01
=
πc
b
(6)
The ω − k plot for m = 0, n = 1, b = 0.02m is shown in Fig. 14.12.For
convenience the variables are chosen as dimensionless.
Fig. 14.12 Dispersion
diagram for the TE
01
mode of
rectangular waveguide for
b = 2cm
At high frequencies, the curve is asymptotic to the line ω −kc. Thus at high
frequencies, both the phase and group velocities approach c. However, the

14.3 Solutions 699
ω − k plot is always above the ω = kc line. This implies that the phase
velocity ν
p
= ω/k is always larger than c.
The group velocity v
g
= dω/dk is determined by the slope of the curve
which is less than the slope of the line ω = kc, and so v
g
is always less
than c.
There is a minimum frequency, known as the cut-off frequency, below
which k becomes imaginary and the wave ceases to exist. As the frequency
approaches the cut-off frequency the phase velocity becomes infinite and
the group velocity becomes zero.
14.104
(a)
∂
2
∂x
2
+
∂
2
∂y
2
E
z
= (k
2
− ω
2
με)E
z
(1)
For TM waves H
z
vanishes, and E
z
must be a solution of (1). Let
E
z
= ( A cos k
x
x + B sin k
x
x)(C cos k
y
y + D sin k
y
y) e
–jkz
(2)
where A, B, C, D are arbitrary constants and k
x
and k
y
are constants to
be determined by boundary conditions. Substitution of (2) in (1) yields
k
2
x
+ k
2
y
= ω
2
με − k
2
(3)
The form of (2) is further constrained by the boundary conditions.
Assuming that the walls of the waveguide are perfect conductors, E
z
which is tangential to the walls must vanish at x = 0, x = a, y = 0
and y = b,Fig.14.13.In(2)E
z
will not vanish at x = 0 unless A = 0.
Similarly the boundary condition at y = 0 is satisfied if C = 0. The
boundary conditions at x = a and y = b are satisfied by putting.
k
x
=
mπ
a
k
y
=
mπ
b
(4)
Fig. 14.13 Rectangular
hollow metal waveguide
