Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

700 14 Electromagnetism II
where m and n are positive integers. Finally, we get the result
E
z
= K sin
m π x
a
sin
n π y
b
e
−jkz
(5)
where K = (B)(D) is another constant. Note that E
z
vanishes if either
m = 0orn = 0. In that case TM
m0
or TM
0n
wave does not exist. The
other field components are given from equations which are obtained by
manipulating Maxwell’s equations.
E
x
=−
j
ω
2
με − k
2
k
∂ E
z
∂x
+ ωμ
∂ H
z
∂y
(6)
E
y
=−
j
ω
2
με − k
2
−k
∂ E
z
∂y
+ ωμ
∂ H
z
∂x
(7)
Using (5) in (6) and (7) and putting H
z
= 0
E
x
=−
jK kmπ
(ω
2
με − k
2
)a
cos
mπ x
a
sin
nπ x
b
e
−jkz
(8)
E
y
=−
jK knπ
(ω
2
με − k
2
)b
sin
mπ x
a
cos
nπ y
b
e
−jkz
(9)
The solutions (5), (8) and (9) represent an infinitely large family of
waves, characterized by different values of the integers m and n.They
differ from one another by the values of the integers m and n.Theyalso
differ in their velocity as well as field configuration.
(b) Combining (3) and (4) we get
k
2
=
ω
2
c
2
−
mπ
a
2
−
nπ
b
2
(10)
where we have substituted με = 1/c
2
. The cut-off frequency is
obtained by setting k = 0.
ω
mn
= π c
m
a
2
+
n
b
2
1/2
(11)
14.105
(a) For TE waves there is no E
z
. Here, we must find boundary conditions
on H
z
that cause the tangential component of E
z
to vanish. The given
equation is
∂
2
∂x
2
+
∂
2
∂y
2
H
z
= (k
2
− ω
2
με) H
z
(1)
14.3 Solutions 701
The general solution is
H
z
= ( A cos k
x
x + B sin k
x
x)(C cos k
y
y + D sin k
y
y)e
−jkz
(2)
∴
∂ H
z
∂x
= (−k
2
A sin k
x
x + Bk
2
cos k
x
x)
(C cos k
y
y + D sin k
y
y)e
−jkz
For
∂ H
z
∂x
= 0atx = 0, it is necessary that B = 0.
Similarly
∂ H
z
∂y
= ( A cos k
x
x + B sin k
x
x)(−Ck
y
sin k
y
y + D cos k
y
y)e
−jkz
For
∂ H
z
∂y
= 0, D = 0. Therefore (2) becomes
H
z
= K cos(k
x
x) cos(k
y
y) e
−jkz
(3)
where K is the product of A and B is another constant. Imposing
boundary conditions at x = a and y = b,wehave
∂ H
z
∂x
=−Kk
x
sin k
x
x cos k
y
y = 0
yielding
k
x
a = mπ (4)
and
∂ H
∂y
=−Kk
y
cos k
x
x sin k
y
y = 0
yielding
k
y
b = nπ (5)
∴ H
z
= K cos
mπ x
a
cos
nπ y
b
(6)
Substituting (2) in (1) we obtain
k
2
x
+ k
2
y
= ω
2
με − k
2
(7)
which is identical with (3) of prob. (14.104).
(b) Substituting the values of k
x
and k
y
from (4) and (5) in (7) and setting
k = 0 gives the cut-off frequency.

702 14 Electromagnetism II
ω
mn
= π c
m
a
2
+
n
b
2
1/2
(8)
which is identical with (11) of prob. (14.104).
(c) Thus the features which are identical for the TM and TE modes are
(i) ω −k plot
(ii) Phase
(iii) Group velocity
(iv) Cut-off frequency
However the important difference is that when either m = 0orn = 0, the
TM mode fails to exist. On the other hand H
z
does not vanish for m = 0
or n = 0 (see (6)). Because of this fact the TE
10
is the mode which has the
lowest cut-off frequency. Here we have assumed that a > b. The cut-off
frequency for TE
10
mode is given by
ω
10
=
π c
a
(9)
the free space wavelength being 2a.
The small dimension (b) has no bearing on the cut-off frequency for this
mode. The other advantage is that single mode operation is feasible over a
wide range of frequencies.

Chapter 15
Optics
Abstract Chapter 15 deals with geometric optics. Problems are solved under
internal reflection in slabs and prisms, fibre optics, matrix methods, Fraunhofer
diffraction by single slit, double slit and grating, missing orders, resolving power,
Rayleigh’s criterion, interference, colours in thin films, Newton’s rings, polarization,
Malu’s law and Brewster’s law.
15.1 Basic Concepts and Formulae
Geometrical Optics
Fermat’s principle: A ray of light traverses from one point to another by a route
which takes least time.
Momentum of photon p = hν/c (15.1)
Fraction ( f ) of light escaping from an isotropic point source in a medium of refrac-
tive index n through a flat surface is given by
f =
1
2
1 −
1
n
n
2
− 1
(15.2)
Intensity of light (I ) at distance r from a point source of power W is related to
pressure P by
P =
I
c
=
W
4πr
2
c
(15.3)
Mirage is a type of illusion formed by light rays coming from the low region of
the sky in front of the observer on a sunny day.
Optical path length (O.P.L.) =
N
i=1
n
i
s
i
(15.4)
where s
i
is the path length of the ray in the ith medium.
703
704 15 Optics
Fibre optics: The maximum acceptance angle θ
max
outside which entering rays
will not be totally reflected within the fibre is given by
n
0
sin θ
max
=
n
2
f
− n
2
c
(15.5)
where n
0
is the refractive index of the medium outside the fibre, n
f
that of the fibre
and n
c
that of the cladding material.
Snell’s law of refraction
n
1
sin
i
= n
2
sin r (15.5a)
where i = angle of incidence and r = angle of refraction.
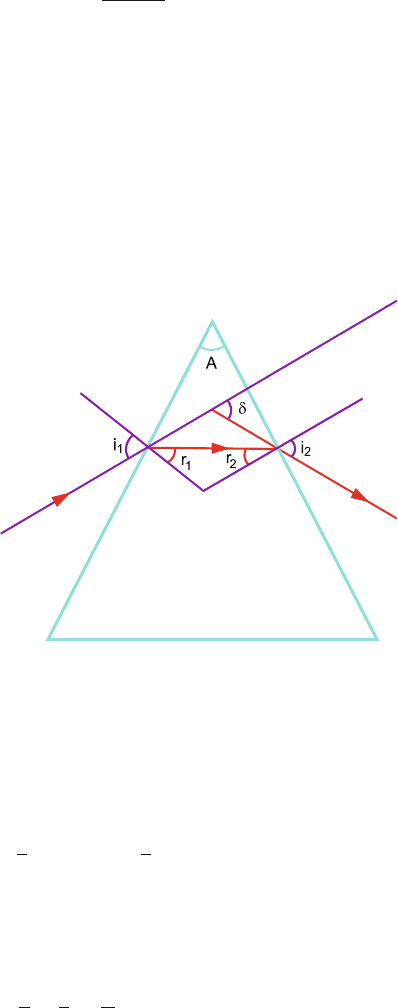
Prisms (Fig. 15.1)
Fig. 15.1
r
1
+r
2
= A (15.6)
δ = (i
1
−r
1
) + (i
2
−r
2
) = i
1
+i
2
− A (15.7)
For minimum angle of deviation
δ = D, i
1
= i
2
, r
1
= r
2
(15.8)
n = sin
1
2
(A + D)/ sin
1
2
(A) (15.9)
If the prism of index n
1
is placed in a medium of index n
2
then n should be replaced
by n
1
/n
2
.
Lenses: Object distance (u), image distance (v) and focal length ( f )
1
u
+
1
v
=
1
f
(15.10)

15.1 Basic Concepts and Formulae 705
Lens Maker’s Formula
Sign Convention
1
F
= (n − 1)
1
r
1
−
1
r
2
(lens maker’s formula) (15.11)
r is positive if the refracting surface facing the object is convex and r is negative
if the refracting surface facing the object is concave.
If the lens of refractive index n
1
is immersed in a medium of index n
2
, then
n = n
1
/n
2
.
Combination of Two Thin Lenses: Let lense L
1
of focal length f
1
facing the
object at distance u
1
and L
2
of focal length f
2
be located at a distance d behind L
1
.
Then the final image is located from L
2
at a distance v
2
given by
v
2
=
f
2
[ f
1
u
1
− d(u
1
− f
1
)]
f
1
u
1
+ (u
1
− f
1
)( f
2
− d)
(15.12)
Magnification =
Height of the final image
Height of the object
(15.13)
If v
2
is positive then the image is real, if v
2
is negative, the image is virtual.
System matrix: I
2
= R
21
T
2
R
12
I
1
(15.14)
where the initial image I
1
in medium 1 is transformed into the final image I
2
in
medium 2. R
12
is the refraction matrix at the first surface (air to glass), T
2
is the
translation matrix in the second medium (glass) and R
21
is the refraction matrix at
the second surface (glass to air).
The matrix S = R
21
T
2
R
12
(15.15)
is known as the system matrix.
Interference
Conditions: Light sources are coherent, i.e. their phase difference remains constant
and that the distance between the sources is reasonably small (of the order of a few
Angstroms for visible light).
Young’s Double-Slit Experiment
x
m
= mλ
D
d
(bright fringes), m = 0, 1, 2,... (15.16)

706 15 Optics
x
m
=
m +
1
2
λ
D
d
(dark fringes), m = 0, 1, 2,... (15.17)
where x
m
is the distance of the mth fringe from the central fringe, D is the source–
screen distance, d is the separation of slits and λ is the wavelength of monochro-
matic light used.
If white light is used, the central fringe will be white, flanked by coloured fringes
on either side with the system of violet fringes closer to the central fringe and red
one farther. In three dimensions the shape of the fringes is that of hyperboloids, and
on the screening the shape would be that of a set of hyperbolas. However, because
of limited field of view the fringes appear as a set of equidistant straight lines. The
separation of fringes is known as bandwidth (β):
β =
λD
d
(bandwidth) (15.18)
Shift of fringes (): When a thin film of thickness t is introduced in the path of one
of the rays
(n − 1)t = mλ (15.19a)
=
D
d
(n − 1)t (15.19b)
and the entire system of fringes undergoes a lateral shift.
The intensity distribution of the fringes is given by
I = 4A
2
cos
2
πdx
λD
(15.20)
The principle of optical reversibility states that if there is no absorption of light, then
a light ray that is reflected or refracted will retrace its original path if its direction is
reversed.
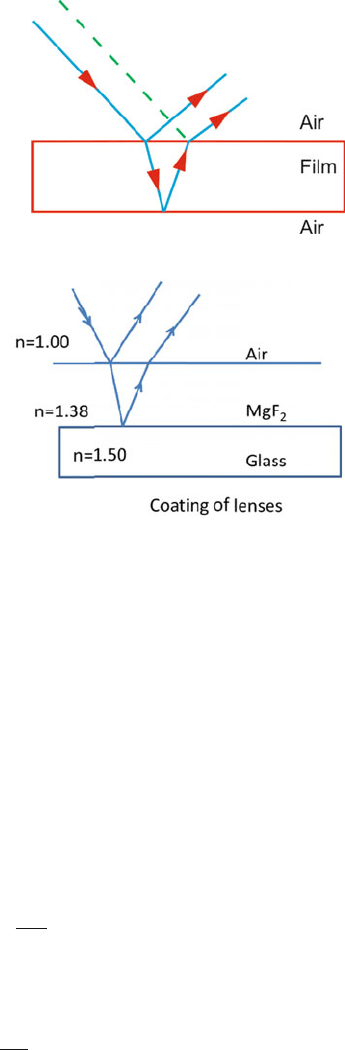
Interference by Reflection from Thin Films
When reflection occurs from an interface beyond which the medium has a lower
index of refraction, the reflected ray does not undergo a phase change; when the
medium beyond the interface has a higher index, there is a phase change of π.The
transmitted wave does not undergo a change of phase in either case.
Thus for air–glass–air media (Fig. 15.2) for normal incidence
2tn = (m + ½)λ, m = 0, 1, 2,...(maxima) (15.21)
The term ½ λ is introduced because of the change of phase of 180
◦
which is equiv-
alent to half a wavelength
2tn = mλ, m = 0, 1, 2,... (minima) (15.22)
15.1 Basic Concepts and Formulae 707
Fig. 15.2
Fig. 15.3
These equations are valid if n of the film is higher (for example, air–glass–air) or
lower (for example, glass–water–glass) than the indices of media on each side of the
film.
For oblique incidence, with refracting angle r, the left-hand side of (15.21) and
(15.22) must be multiplied by cos r.
For coating lenses, Fig. 15.3 shows a typical arrangement in which the indices of
the media are in the ascending order. Here the conditions are reversed:
2tn = mλ, m = 0, 1, 2 ...(maxima) (15.23)
2tn = (m + ½)λ, m = 0, 1, 2 ...(minima) (15.24)
Wedge film
β =
λ
2nθ
(15.25)
where θ is the angle of the wedge.
Biprism β =
λD
2d
(bandwidth) (15.26)
708 15 Optics
Newton’s Rings (in Reflected Light)
Radius of the mth ring (r
m
) for the convex lens of radius R is given by
r
m
=
√
mλR (dark rings, m = 0, 1, 2, ...) (15.27a)
2t = mλ (dark rings) (15.27b)
r
m
=
m +
1
2
λ (bright rings, m = 0, 1, 2, ...) (15.28a)
2t = (m + ½)λ (bright rings) (15.28b)
where t is the thickness of air gap.
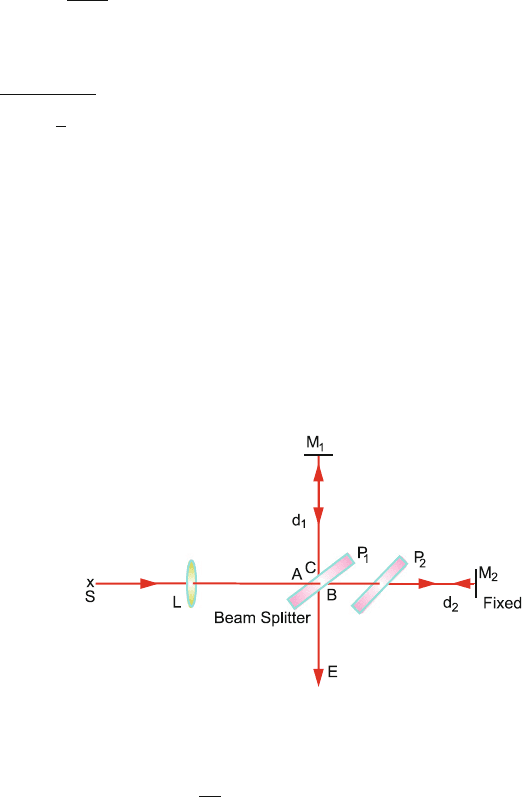
Michelson’s Interferometer
M
1
and M
2
are two plane mirrors mounted (Fig. 15.4), M
1
being movable and M
2
fixed. The plate P
2
compensates for the extra pathlength in P
1
. The interference
fringes form from the superposition of the two beams and are viewed at E (see
prob. 15.38).
Fig. 15.4
The mirror displacement L when n fringes cross the field of view is given by
L =
nλ
2
(15.29)
Diffraction (Fraunhofer)
Single slit a sin θ = mλ (minima, m = 1, 2, 3, ...) (15.30)
where a is the slit width and θ is the diffraction angle.
15.1 Basic Concepts and Formulae 709
Relative intensities of the secondary maxima
I
θ
= I
max
sin α
α
2
(15.31)
where α =
πa
λ
sin θ (15.32)
I
θ
I
max
=
⎛
⎜
⎜
⎝
sin
m +
1
2
π
m +
1
2
π
⎞
⎟
⎟
⎠
2
(15.33)
The secondary maxima lie approximately halfway between the minima.
Double-Slit and N-Slits (Grating)
I = I
max
sin α
α
2
sin
2
Nβ
sin
2
β
(15.34)
where α =
πa sin θ
λ
and β =
πd sin θ
λ
a is the slit width and d is the slit spacing. In (15.32) the first factor arises due to
diffraction from a single slit, the second one is due to interference of light waves
from different slits.
For N = 1 we obtain the single-slit pattern and for large N we are dealing with
a grating.
Maximum number of order m
max
= a/λ (15.35)
Condition for overlapping of spectral lines:
m
1
λ
1
= m
2
λ
2
= m
3
λ
3
= ... (15.36)
Missing orders: The missing orders occur when the condition f or a maximum of
the interference and for a minimum of the diffraction are both fulfilled for the same
value of θ:
d sin θ = mλ, m = 0, 1, 2 ...
a sin θ = pλ, p = 1, 2, 3,...
d
a
=
m
p
(15.37)
