Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

730 15 Optics

Fig. 15.17 Refractionina

prism

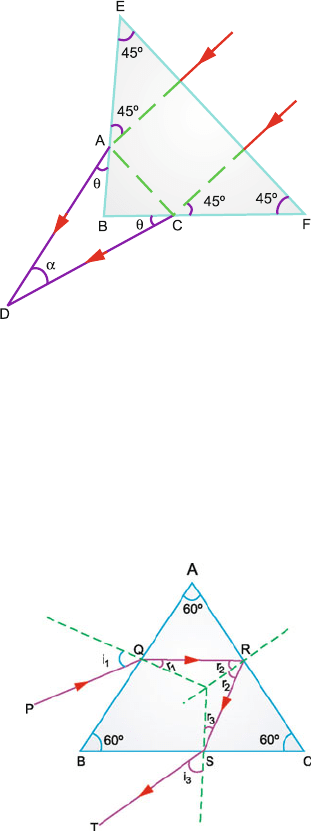
15.8 The net deviation of the ray

δ = (i

−r

) + (360

◦

− 2r

) + (i

−r

) (1)

In the minimum angle position, r

= r

= A/2 = 60/2 = 30

◦

From the geometry of Fig. 15.18, r

= 30

◦

Fig. 15.18 Deviation of a ray

incident in the minimum

deviation position of the

prism after suffering one

internal reﬂection

By Snell’s law

Sin i

= n sin r

= 1.5 ×sin 30

◦

= 0.75

∴ i

= 48.59

◦

Similarly, i

= 48.59

◦

∴ δ = (48.59 − 30

◦

) + (360 − 2 × 30

◦

) + (48.59 − 30

◦

) = 337.18

◦

15.3 Solutions 731

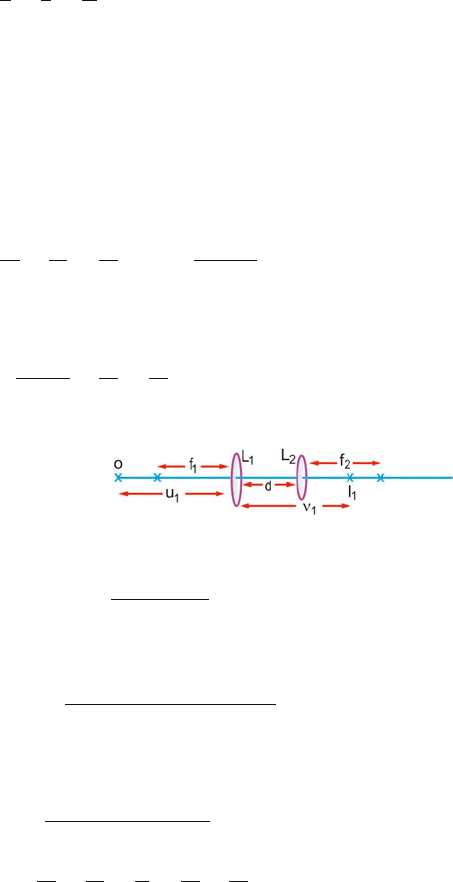
15.9

where u, the object distance, and v, the image distance, are measured from the

centre of the lens. For real object and image u and v are positive, for virtual

object or image u and v are negative. f is positive for convex lens and negative

for concave lens.

Let the object o be placed at distance u

from lens L

of focal length f

.The

second tens L

is placed at distance d behind L

,Fig.15.19. The image I

formed at distance v

from the lens L

, alone. Then from the lens equation

or ν

− f

(1)

The image acts as an object for the second lens L

(real or virtual)

−

− d

Fig. 15.19 Image due to combination of two lenses, a distance d apart

whence v

− d)

+ v

− d

Substituting ν

from (1) and simplifying

= f

[ f

− d(u

− f

)]

+ (u

− f

)( f

− d)

(2)

In the limit d → 0, (2) reduces to

+ f

− f

15.10 The location of the object, the screen and the positions of the lens are indi-

cated in Fig. 15.20

(a)

+ v

= D (1)

− u

= d (2)

732 15 Optics

Fig. 15.20 Real images

formed by a convex lens in

two positions

By symmetry v

= u

(3)

= u

(4)

Then (2) becomes

− v

= d (5)

size of image

size of object

(6)

Similarly,

(7)

∴

(8)

From (1) and (5), v

D + d

and v

D − d

Therefore,

(D − d)

(D + d)

(b) Multiplying (6) and (7)

= 1

∴ O =



(c)

∴

D + d

D − d

where we have used (1), (2) and (4).

∴ f =

− d

15.3 Solutions 733

(d) From the result of (c),wehave

(D − 4 f )

Since d

must be positive, it follows that D > 4 f .

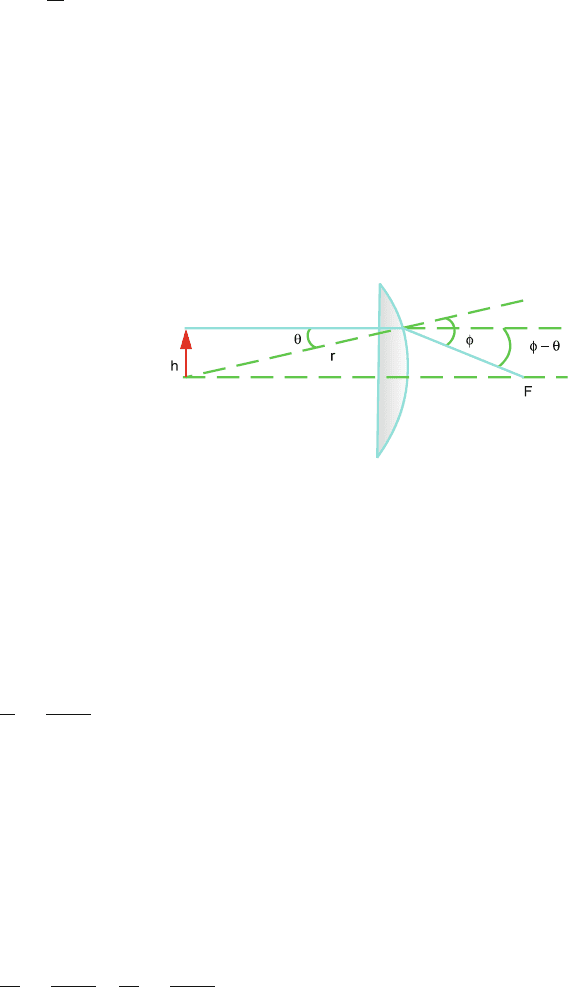
15.11

(a) Consider a plano-convex lens of focal length f . Let a paraxial ray be

incident on the lens from a small object of height h. After striking the

plano-convex lens normally, it gets refracted at the convex surface and

passes through the principle focus F, behind the lens, Fig. 15.21.Letθ

be the angle of incidence at A, the angle being measured with the radius

of curvature of the curved surface r.Letφ be the angle of refraction:

Fig. 15.21

sin φ = n sin θ(Snell’s law)

φ = nθ(∵ angles are small) (1)

Also θ = h/r,φ− θ = h/ f (2)

Combining (1) and (2)

n − 1

(3)

We use the convention that r is positive if the refracting surface facing

the object is convex and r is negative if the refracting index facing the

object is concave.

A thin lens may be considered as two plano-convex or two plano-

concave lenses in contact. Thus a thin biconvex lens whose faces have

radii of curvature r

and r

are considered as two plano-convex lenses

with their plane surfaces cemented together:

n − 1

−r

(4)

734 15 Optics

∴

= (n − 1)



−



(lens maker’s formula)

(5)

For a biconvex lens r

is positive and r

negative. For double-concave

lens r

is negative and r

positive.

(b) If the lens of refractive index n

is immersed in a medium of index

, then n = n

, n = 1.2/1.33 = 0.9, and the ﬁrst bracket in (5)

becomes n − 1 =−0.1 resulting in a negative value of F. Thus the

plastic lens immersed in water acts as a diverging lens.

15.12

(a) The ﬁrst image due to L

alone is formed at I

at a distance v

given by

∴ v

− f

5 × 10

5 − 10

=−10 cm

The image is formed at 10 cm in front of the lens (Fig. 15.22).

Fig. 15.22 Image due to

combination of two convex

lenses

(b) The image is virtual (∵ v is negative) and erect.

is located at distance ν

from lens L

given by the

result of prob. (15.9),

[ f

− d(u

− f

)]

+ (u

− f

)( f

− d)

(1)

Here u

= 5cm,d = 10 cm, f

= 10 and f

= 12 cm.

Substituting these values in (1) we ﬁnd v

= 30 cm behind the lens L

(d) The ﬁnal image is real (∵ v

is positive) and inverted.

15.13 Let a ray PA enter the sphere at A, refract at A and B and intersect the axis at

F (Fig. 15.23). Let φ be the angle of incidence and θ the angle of refraction

at A:

Sin φ = μ sin θ (Snell’s law) (1)

φ = μθ (∵ angles are small) (2)

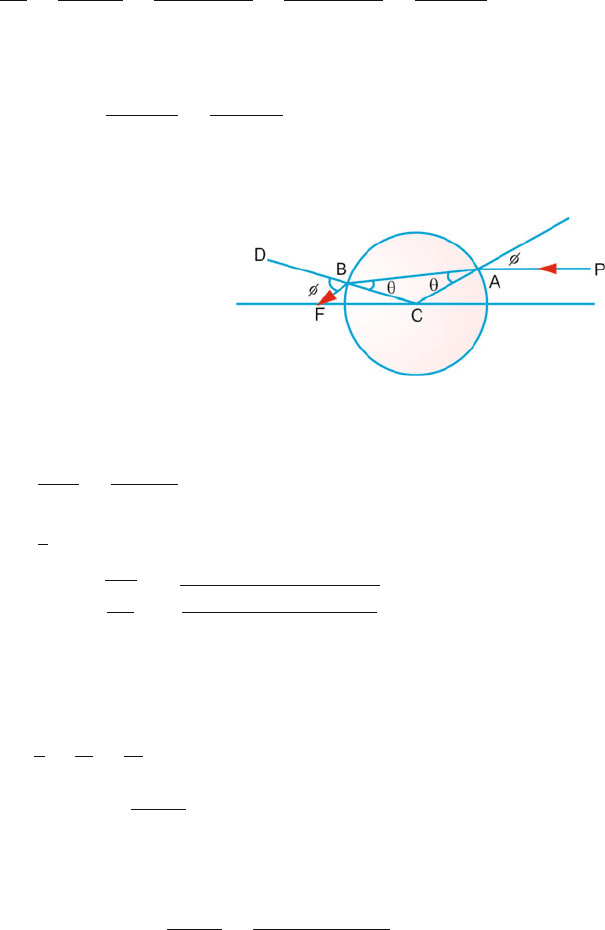
15.3 Solutions 735

In BFC,

sin F

sin B

sin(π −φ)

sin 2(φ − θ)

sin φ

sin 2(φ − θ)

2(φ − θ)

(3)

since the angles are small. Hence the equivalent focal length

= FC =

BCφ

2(φ − θ)

μr

2(μ − 1)

(4)

where we have used (2), (3) and (4).

Fig. 15.23

15.14 The intensity at a distance r is given by

I =

4πr

100

4π ×5

= 0.318 W/m

I =

∴ E



2 I



2 × 0.318

8.85 × 10

−12

× 3 × 10

= 15.48 V/m

15.15

(a) If the object distance is u then the distance v

at which the image is

formed by objective is given by

or v

=−

u − f

(1)

The distance of this image from the eyepiece, u

is given by

= f

+ f

−

u − f

− f

u − f

(2)

where f

+ f

is the distance between the objective and eyepiece.

736 15 Optics

If the ﬁnal image is formed at a distance v from the eyepiece then

−

u − f

− f

or v =−

(uf

− f

)

(3)

Now u >> f

, f

∴ v =−u





= 10





= 156.25 m

(b)

M =

Height of the ﬁnal image

Height of the object

−

=−

=−0.125

where we have used (1), (2) and (3).

∴ Height of ﬁnal image = (height of the object).M

=−100 × 0.125 =−12.5m

The negative sign indicates that the ﬁnal image is virtual.

Note that the height of the image is only one-eighth of that of the

object, but the image is closer than the object by a factor of 64, so it

subtends an angle eight times large, that is, the image appears eight times

larger.

15.16

(a) The Intensity is given by

I =

power

cross-section

1000

−5

× 10

−4

= 10

W/m

(b)

I =



2 × 10

8.85 × 10

−12

× 3 × 10

= 2.74 ×10

V/m

15.3 Solutions 737

15.3.3 Matrix Methods

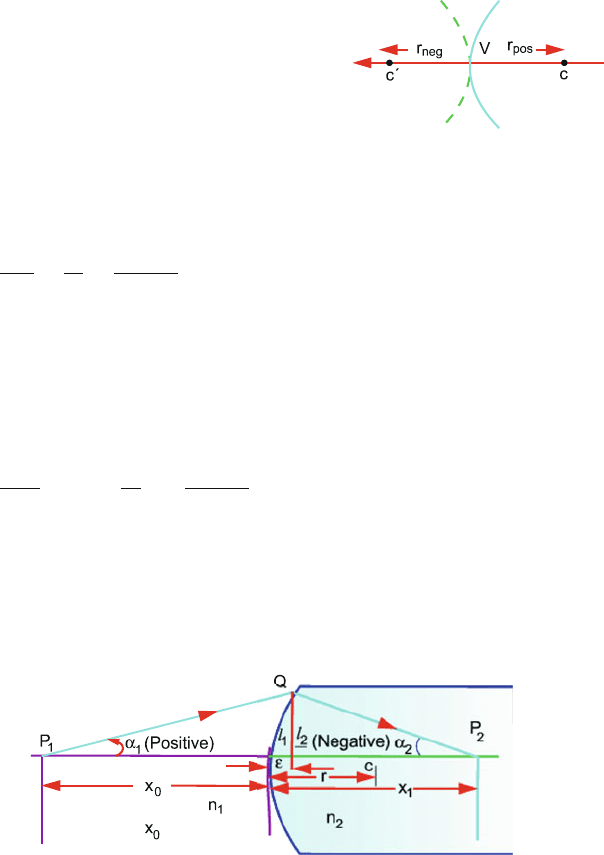
15.17 Assume that light is always incident from the left, then the refracting surface

is convex if r is positive (from V to C) and concave if r is negative (from V

to C



), Fig. 15.24.

Fig. 15.24 Light is incident

from left. Sign convention for

refraction at a curved optical

surface

The symbols used are object distance x

, object size y

, image distance x

image size y

and radius of curvature, r. The object–image equation can be

written as

−x

− n

(1)

The convention r esults in negative value for the object distance. Paraxial rays

are considered so that α

and α

are small. Each ray is given a height and

an angle, Fig. 15.25. The distance ε on the axis, called sagitta, is nearly

zero. Considering counterclockwise angles as positive and clockwise angles

as negative (1) becomes

+ n



−



− n

(2)

As l

= l

, two simultaneous equations can be written in the variables α

and l

( j = 1, 2):

= l

(3)

Fig. 15.25 Passage of a light ray P

in medium of refractive index n

into medium of refractive

index n

onto P

738 15 Optics

−



− n



(4)

In the matrix form (3) and (4) can be written as





⎛

⎝



− 1



⎞

⎠





(5)

The initial image in medium 1 described by the column vector I





transformed into the ﬁnal image in medium 2 described by the column vector





. The transformation is accomplished by the refraction matrix

⎛

⎝



− 1



⎞

⎠

(6)

In the matrix notation (5) is written as

= R

(7)

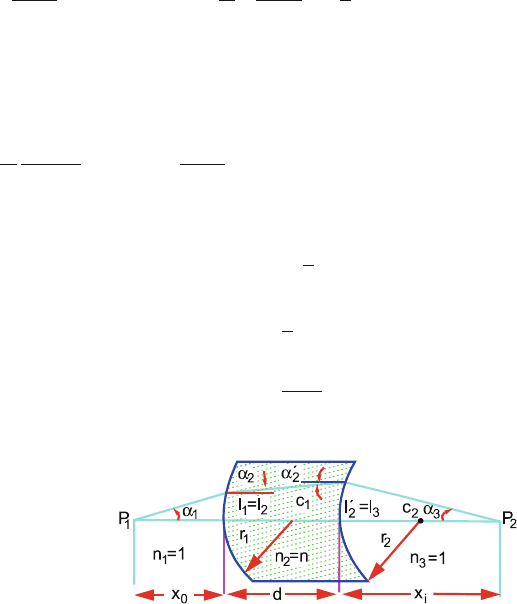
Next consider a parallel translation of a ray through a distance d in some

homogeneous medium, Fig. 15.26.

Since α

= α

, for small angles

= l

+ α

d (8)

In matrix form (8) can be written as







1 d





(9)

or I

= T

(10)

Fig. 15.26 Sequences of

refraction, translation and

refraction for a thick lens

placed in air

15.3 Solutions 739

where the translation matrix is



1 d



(11)

In Fig. 15.26, the overall transformation can be written as

= R

(12)

where R

is the refraction matrix at the ﬁrst surface (air to glass), T

is the

translation matrix in the second medium (glass) and R

is the refraction

matrix at the second surface (glass to air). The matrix R

is known as

the system matrix.

15.18 Consider two curved surfaces of positive radii of curvature, r

and r

.The

ﬁnal image in Fig. 15.27 is obtained from the equation:





⎛

⎝

n − 1

⎞

⎠





⎛

⎝



1 − n



⎞

⎠





Symbolically,

= R

Let P

(1 − n)

and P

n − 1

Then



















⎛

⎜

⎝

1 + dP

+ dP

+ nP

+ 1

⎞

⎟

⎠





Fig. 15.27 Refractionina

double convex lens of

thickness d placed in air