Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

750 15 Optics

15.35 2μt cos r =



m +



λ (maxima), m = 0, 1, 2 ...

r = 0,μ= 1

λ =

m +

2 × (2945 Å)

m +

5890

m +

For m = 0,λ= 11,980 Å

m = 1,λ= 3927 Å

m = 2,λ= 2356 Å

λ = 3927 Å falls within the range of visible spectrum. The colour is violet.

15.36 2μt cos r =



m +



r = 0, m = 0

t = λ/4μ

15.37 For constructive interference

2μt cos r =



m +



λ, m = 0, 1, 2 ...

sin r =

sin i

sin 30

◦

1.5

= 0.3333

∴ cos r = 0.9428

λ =

2μt cos r

m +

2 × 1.5 × 4 × 10

−5

× 0.9428

m +

For m = 1, we ﬁnd λ = 7.542 × 10

−5

cm = 7542 Å.

15.38 (a) The two mirrors M

and M

are adjusted such that their distance from

the beam splitter are approximately equal, Fig. 15.4. The wavelengths

and λ

for the D

and D

lines of sodium differ only by a few

angstroms. Two different sets of fringes arise due to two wavelengths.

If M

is slowly moved away there is a gradual separation of the two

sets, and ﬁnally the bright band of the one lies over the dark band of

the other, resulting in uniform illumination. Thus the fringes disappear

and reappear periodically. Between two successive disappearances the

mirror has to be moved by, say d cm. This corresponds to a path differ-

ence of 2d cm. Assuming that λ

<λ

, this path difference must contain

exactly one more wavelength of λ

than of λ

. Thus expressing λ

and

in cm,

15.3 Solutions 751

−

= 1

∴ λ

− λ

= λ =

(b) λ =

(5.89 × 10

−5

)

2 × 2.89 × 10

−5

= 6Å

15.39 λ =

2 × 2.948 × 10

−3

100

= 5.896 ×10

−5

cm = 5896 Å

15.40 Resolving power

λ

gπ D

where D = distance between the plates = 2mm= 0.2cm:

λ = 600 nm = 6 × 10

−5

g =

1 −r

2 × 0.9

1 − (0.9)

= 9.4737

R. P =

λ

9.4737 × 3.14 × 0.2

6 × 10

−5

= 9.9 ×10

15.3.5 Diffraction

15.41

a sin θ = mλ (1)

∴ sin θ =

mλ

= 1 ×

(2)

If D is the slit screen distance and x the distance of the ﬁrst minimum from

the central maximum, then

tan θ  sin θ = x/D (3)

Combining (2) and (3)

λ =

0.02 × 0.5

200

= 5 ×10

−5

cm = 5000 Å

15.42 I

= I



sin α



Differentiating I

with respect to α and setting

dα

= 0,

dα

(2α

sin α cos α − 2α sin

α)

= 0

752 15 Optics

∴ 2α sin α(α cos α − sin α) = 0

∴ tan α = α

15.43

(a) The half-width is the angle between the two points in the pattern where

the intensity is one-half the centre of the pattern:



sin α



(1)

The solution of (1) found by numerical method is

= 1.40 rad (2)

πa

sin θ

= 1.40 (3)

where θ

θ.

sin θ

1.4λ

πa

or θ

= sin

−1



1.4λ

πa



or θ = 2θ

= 2sin

−1



1.4λ

πa



(b) θ = 2sin

−1



1.4

4π



= 12.8

◦

15.44

a sin θ = mλ

a sin θ

= 1 ·λ

a sin θ

= 2λ

But θ

= θ

∴ λ

= 2λ

15.45

sin θ =

nλ

∴ a =

nλD

2 × 5.6 × 10

−5

× 200

1.6

= 0.014 cm

= 0.14 mm.

15.46

(a) Let m be the order of interference. If the slit width a is maintained con-

stant and the separation of the slits d is varied, the scale of the interfer-

ence pattern varies, but that of the diffraction pattern remains unchanged.

If the diffraction angle corresponds to the minimum given by (1) then a

particular order of interference maxima may be absent. This is called a

15.3 Solutions 753

missing order. Thus, a missing order is realized for an angle θ for which

the following two equations are simultaneously satisﬁed:

d sin θ = mλ(m = 1, 2, 3 ...) (1)

a sin θ = nλ(n = 1, 2, 3 ...) (2)

Dividing (1) by (2)

(3)

Since m and n are both integers, missing orders will occur when d/a is

in the ratio of two integers. Expressing d as the sum of the slit width a

and the opaque space b between consecutive slits, that is

d = a + b (4)

(3) an be written as

a + b

(5)

In particular, if

a+b

= 1, b = 0. In this case t he ﬁrst-order spectrum

will be absent and the resultant diffraction pattern will be similar to that

of a single slit.

a+b

= 2, a = b, that is the width of the slit is equal to the width of

the opaque space. Here the second-order spectrum will be absent.

(b)

a + b

0.16 + 0.8

0.16

= 6 =

The above relation is satisﬁed for

n = 1, 2, 3,...

m = 6, 12, 18,...

Thus the order 6, 12, 18, etc. of the interference maxima will be missing,

in the diffraction pattern.

15.47 The central diffraction peak is limited by the ﬁrst minima. The angular loca-

tions of these minima are given by

a sin θ = λ(∵ m = 1) (1)

754 15 Optics

The angular locations of the bright interference fringes are given by

d sin θ = mλ(m = 0, 1, 2 ...) (2)

We can locate the ﬁrst diffraction minimum within the double-slit fringe pat-

tern by dividing (2) by (1)

n =

0.2

0.012

= 16.66

Therefore 16 interference fringes will lie within the central maximum.

15.48 m

= m

× 5460 = 4095 Å

15.49 d sin θ = mλ

For m = m

max

,θ = θ

max

= 90

◦

, Given

= 5000

max

5000

6 × 10

−5

= 3.33

∴ m

max

= 3

15.50

(condition for missing orders)

0.3

0.1

where m and n are integers. The above relation is satisﬁed for

m = 3, 6, 9

n = 1, 2, 3

Thus the maxima will be missing in the third, sixth, ninth, etc. orders.

15.51

a + b

a + 2a

= 3 =

The above relation is satisﬁed for

m = 3, 6, 9,...

n = 1, 2, 3,...

15.3 Solutions 755

Thus the interference maxima will be missing in the third, sixth, ninth, etc.

orders.

15.52

(max) =

Nλ

4000 × 4 × 10

−5

= 6.25

(max) =

Nλ

4000 × 7 × 10

−5

= 3.57

The maximum order of spectrum varies between 3 (towards red) and 6

(towards violet).

15.53

a + b

a + a

= 2 =

(condition for missing orders)

∴ m = 2n

The above condition is satisﬁed for

n = 1, 2, 3 ...

m = 2, 4, 6 ...

Thus all the even orders of interference fringes (2, 4, 6, ...), except m = 0,

are missing.

15.54 The secondary maxima lie approximately halfway between the minima.

Now, the intensity at an angle θ is given by

= I



sin α



(1)

where α =

π a

sin θ (2)

Minima occur in (1) when

α = mπ(m = 1, 2, 3 ...) (3)

Therefore the ﬁrst secondary maximum would occur halfway between ﬁrst

minimum and second minimum. Therefore,

α =



m +



π =

3 π

(4)

Substituting (4) into (1)



sin(3π/2)

3πl2



= 0.045 or 4.5%

756 15 Optics

15.55 In Fig. 15.34 the grating space AD = d.IntheABD, B

AD = i, the angle

of incidence. Also D

AC = θ, the angle of diffraction. In the ABD, BD the

path difference between the incident rays, YD and XA is

BD = d sin i

Fig. 15.34 Diffractionbya

grating for a parallel beam of

light which is obliquely

incident

Similarly, the path difference between the diffracted rays is

DC = d sin θ

The total path difference

BD + DC = d(sin i +sin θ) (1)

For the mth primary maximum

d(sin θ

+ sin i) = mλ (2)

or sin





mλ

2d cos



−i



(3)

The angle of deviation of the diffracted beam is

= θ

+i (4)

For δ

to be minimum, cos

−i

must be maximum, that is

(θ

−i)/2 = 0 → θ

= i (5)

15.3 Solutions 757

Then δ

will be minimum, say D

, and is given by

= θ

+i = 2i

or i = D

/2(6)

Substituting (5) and (6) into (3)

2d sin





= mλ (7)

N =

2sin(20/2)

1 × 4.358 × 10

−5

= 7969 lines/cm

15.56 Condition for overlapping is

mλ

= (m + 1)λ

5400 m = 4050 × (m + 1)

∴ m = 3

d sin θ = mλ

N =

sin θ

mλ

sin 30

◦

3 × 5.4 × 10

−5

= 3086 lines/cm

15.57

λ = 5893 Å = 5.893 × 10

−5

λ = λ

− λ

= 5896 −5890 = 6Å= 6 × 10

−8

Resolving power

R =

dλ

5.893 × 10

−5

6 × 10

−8

= 982

R = Nm

∴ N =

982

= 491 (Total number of lines)

If N



is the number of lines/cm, then the width of the grating

W =



491

800

= 0.614 cm

15.58 Total number of lines on the grating

N = N



W (1)

758 15 Optics

where N



= number of lines/in. and W is the grating width (in inch)

∴ N = 10, 000 ×3 = 30, 000

R =

dλ

= Nm

∴ dλ =

6 × 10

−5

3 × 10

× 1

= 2 ×10

−9

cm = 0.2Å

15.59 Total number of lines

N = N



W = 2 ×425 = 850

λ = 5893 Å, dλ = 5896 −5890 = 6Å

(i) First order:

R =

dλ

= Nm

N =

dλ

5893

= 982 lines

As the required number of lines (982) exceeds the total number of lines

(850) the lines are not resolved in the ﬁrst order.

(ii) Second order

N =

dλ

5893

= 491

As the required number of lines (491) is less than the total number of

lines, the lines are resolved in the second order.

15.60 The resolving power for a prism of base length B is given by

R =

λ

Bdμ

dλ

(1)

where dμ/dλ is the variation of refraction index of the prism with wave-

length, λ is the mean wavelength and λ is the difference in wavelengths to

be resolved:

λ = 5893 Å,λ = 5896 − 5890 = 6Å

dμ

dλ

1.6635 − 1.6545

(6563 − 5270) × 10

−8

= 696/ cm

Substituting the above values in (1) and solving for B, we ﬁnd the length of

the base of the prism, B = 1.41cm.

15.3 Solutions 759

15.61 The limit of resolution of a telescope is

dθ = 1.22

1.22 × 55 × 10

−5

500

= 1.342 ×10

−7

rad

If the distance between two points is x and the moon–earth distance r, then

x = r dθ = 3.8 × 10

× 1.342 × 10

−7

m = 51 m

15.62 θ =

1.22λ

1.22 × 5.89 × 10

−7

30 × 10

−6

= 0.024 rad

15.63 I = I



(ρ)



where ρ =

2π

a sin θ and J

(ρ) is the Bessel function of the ﬁrst kind.

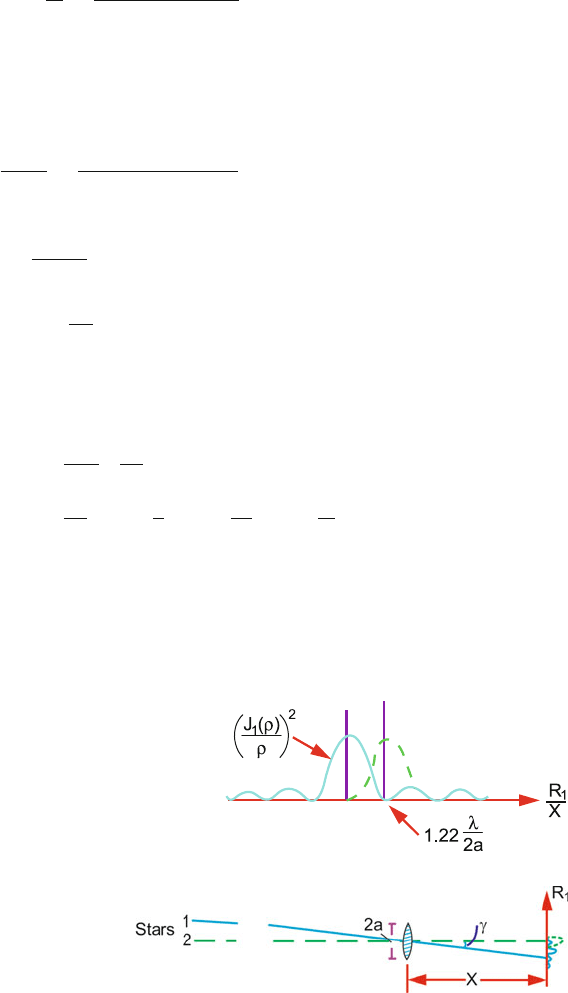
According to the Rayleigh criterion, the separation of the peaks is equal to the

distance between the ﬁrst minimum and the centre of the diffraction pattern,

that is, the ﬁrst minimum of the Bessel function is at ρ = 3.83, and we have

ρ = 3.83 =

2πa





or γ =

= 0.61

= 1.22

where 2a = D is the diameter of the lens, γ is the angle between the two

stars, the distance between the observation screen and the lens is X (equal

to focal length of the lens) and the position of the details of the diffraction

pattern is R

,Fig.15.35a, b.

Fig. 15.35 a Intensity

distribution for diffraction

from a circular aperture

described by Bessel function

Fig. 15.35 b Resolution of

diffraction patterns for two

stars, the angle between them

being γ . For the explanation

of parameters X, R

and ρ,

see the text